Advances in Porous Flow
Vol.08 No.02(2018), Article ID:25326,13
pages
10.12677/APF.2018.82004
Research on Logistic Model of Hydraulic Gradient in One-Dimensional Consolidation of Saturated Clay
Jinzhu Li1, Lu Lan1,2, Xinyu Xie1,2
1Ningbo Institute of Technology, Zhejiang University, Ningbo Zhejiang
2Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou Zhejiang

Received: May 21st, 2018; accepted: May 31st, 2018; published: Jun. 7th, 2018

ABSTRACT
During the consolidation of saturated clay, the drainage rate is positively related to hydraulic gradient. The formula and changeable curve with time of hydraulic gradient are acquired based on Terzaghi’s one-dimensional consolidation, and the “S” type curve is explained in the paper. Logistic function is used instead of complex formula of hydraulic gradient through nonlinear fitting. The relationships between function parameters and soil consolidation parameters are defined to establish Logistic model. One-dimensional consolidation of saturated clay in instantaneous and linear loading conditions is simulated with FEM software, thus comparing changeable curves of hydraulic gradient in two conditions which fits well with Logistic function. The results indicate that Logistic model can not only quantitatively describe variation of hydraulic gradient in Terzaghi’s one-dimensional consolidation, but also other consolidation conditions such as linear loading.
Keywords:Saturated Clay, One-Dimensional Consolidation, Hydraulic Gradient, Logistic Model
Logistic模型在软黏土一维固结水力梯度预测中的应用
李金柱1,兰璐1,2,谢新宇1,2
1浙江大学宁波理工学院,浙江 宁波
2浙江大学滨海和城市岩土工程研究中心,浙江 杭州

收稿日期:2018年5月21日;录用日期:2018年5月31日;发布日期:2018年6月7日

摘 要
饱和土体固结过程中,排水速率与水力梯度正相关,研究水力梯度随时间的变化规律有助于了解固结速率的变化过程。以一维固结理论为基础,求取水力梯度随时间变化的曲线,并分析曲线上升段和下降段均呈S形的原因。拟合将复杂的水力梯度表达式拟合为Logistic函数,根据无量纲法确定函数各参数,建立水力梯度的Logistic模型。通过有限元模拟瞬时加载和线性加载两种工况下饱和黏土一维固结问题,得到两种工况下水力梯度变化曲线,并用Logistic函数进行拟合,拟合效果均较好。研究结果表明,水力梯度的Logistic模型不仅可定量描述Terzaghi一维固结的水力梯度变化规律,还适用于线性加载等工况。
关键词 :饱和黏土,一维固结,水力梯度,Logistic模型

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
水力梯度是指沿水流方向单位渗透途径上的水头损失,也可理解为水流为克服摩擦阻力在单位长度渗透途径所耗失的机械能或是驱动力所做的功 [1] 。固结过程中土体受荷后产生初始静水压力,排水面附近的水压力差又使得静水压力变成动水压力,增大了土体内部的水力梯度,固结排水过程开始。随着孔隙水的排出,超孔隙水压力减小,有效应力增大至稳定,主固结完成 [2] [3] [4] 。
水力梯度是联系渗流和有效应力变化两个过程的重要参数,研究水力梯度在固结过程中随时间变化的规律有助于更深入分析固结过程。在渗流方面,Hansbo [5] 提出竖向排水非Darcy渗流幂指数公式,并在此基础上推导适用性更广的固结方程;谢康和 [6] 根据萧山软土固结渗透试验提出了折线渗流模型;不少学者结合土体孔隙水和孔隙的微观性质描述渗透过程中不同阶段渗透速度和水力梯度的变化,揭示非线性渗流的原因 [7] [8] [9] [10] ;Fenton [11] 从数学分析角度预估水力梯度的极值,并得出渗透系数的变化对水力梯度变化范围影响不大的结论。固结方面相关理论发展得比较成熟,无论是Terzaghi一维固结、Biot三维固结等小应变固结理论还是Gibson等大应变固结理论,孔隙水压力和水力梯度的变化规律与土体本身性质联系较大 [12] [13] 。
总体来说,固结过程中水力梯度的变化规律研究甚少。扬少丽 [14] 通过负压沉罐试验测定桶基内不同深度孔压,并绘制了粉土渗流梯度随时间的曲线,得出水力梯度先增大后减小的结论。宰金珉 [15] 、梅国雄 [16] 提出Logistic函数对预估固结沉降的有效性,与水力梯度有一定的联系。本文基于一维固结理论作出水力梯度的变化曲线,分析得到水力梯度Logistic模型,求解水力梯度极值和拐点,定量地描述固结过程中水力梯度随时间变化的规律。
2. 水力梯度曲线的一般描述
关于固结求解的理论推导研究较多,可由此得到水力梯度公式 [12] 。本文基于Terzaghi一维固结理论得到水力梯度公式:
(1)
式中:i为水力梯度; 为水的重度,kN/m3;z为土层深度,m;H为土体厚度,m;p为固结压力,kPa;n为无量纲整数, ; 为时间因子。
(2)
(3)
式中: 为固结系数,m2/s;t为时间,d;k为渗透系数,m/s; 为压缩模量,MPa。
式(1)中水力梯在固结过程中随时间的变化曲线形态如图1所示。
由图可知,土体在固结过程中,水力梯度先增大后减小,变化曲线呈上升和下降两阶段。上升阶段由于饱和粘土渗透性比较差,短时间内水的出流速度较慢,孔隙水压力最初沿深度变化较小,之后水压压差逐渐增大,水力梯度由零增长至最大值,上升曲线呈S型。曲线上升过程中必存在拐点1,使得水力梯度加速度先增大后减小;下降阶段孔隙水压力消散至稳定,水压压差逐渐变小,水力梯度缓慢减小趋于零,主固结大体完成。且下降阶段水力梯度减小时必存在拐点2,使得下降曲线呈反S型。
3. 水力梯度的Logistic模型
3.1. Logistic模型
根据水力梯度的变化规律,S型的成长曲线Logistic函数分别拟合上升和下降阶段的变化曲线效果最好,可用下式描述:
(4)
式中: 、 为与曲线的最高点和最低点相关的参数; 、 为待定参数。
Logistic函数和水力梯度两阶段曲线具备有界性、单调递增性及存在反弯点等共性。公式(4)对t进行
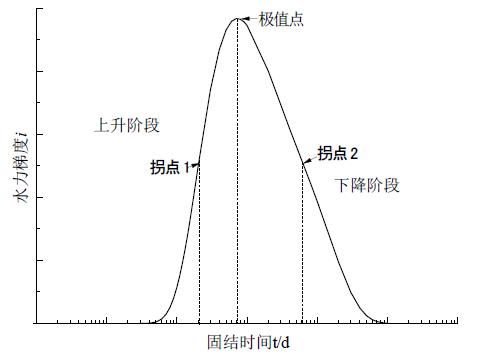
Figure 1. Variation of hydraulic gradient with time
图1. 水力梯度随时间变化图
一阶、二阶求导,可得曲线极值和拐点。
(5)
(6)
式(5)、式(6)分别作图2和图3,由于一阶导数只能无限趋近于零,难以确定极值点,即水力梯度最大值
的坐标。故修正极值的求解,取
,使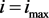 为曲线峰值,则在上升段可求极值点见式(7),上升段和下降段的拐点见式(8)。
为曲线峰值,则在上升段可求极值点见式(7),上升段和下降段的拐点见式(8)。
(7)
(8)
式中: 为水力梯度曲线取极值的时间,d;
和
为水力梯度曲线取极值的时间,d;
和 分别为水力梯度曲线上升和下降段拐点的时间,d;
分别为水力梯度曲线上升和下降段拐点的时间,d;
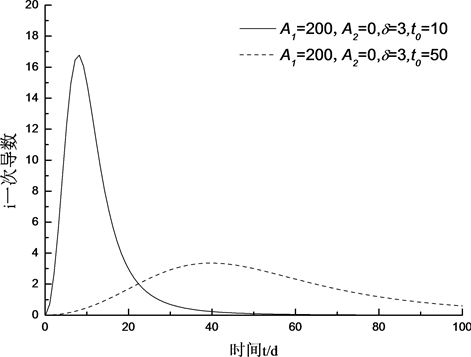
Figure 2. First derivative of Logistic function
图2. Logistic函数一阶导数随时间变化图
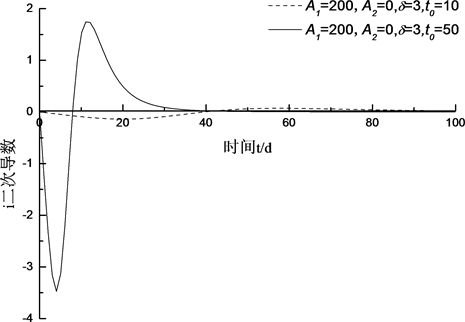
Figure 3. Second derivative of Logistic function
图3. Logistic函数二阶导数随时间变化图
为修正系数,此算例中取1.03。
3.2. 算例分析
固结压力为
,瞬时加载,超孔隙水压力如图4,渗透系数
,压缩模量 ,初始孔隙比
,初始孔隙比 ,分别取土体厚度H为1.0 m、5.0m、10.0m,顶面排水,底面不排水,不考虑土体自重,如图4所示。
,分别取土体厚度H为1.0 m、5.0m、10.0m,顶面排水,底面不排水,不考虑土体自重,如图4所示。
由式(1)可知,固结过程中水力梯度与固结压力、土体厚度、土层深度、固结系数有关。
图5为不同土体厚度和土层深度的水力梯度变化图。结合式(1)和图5可知:上升段曲线形态主要与土层深度z、固结系数cv相关,下降段曲线形态与z、cv和土体厚度H均相关;可见,水力梯度变化主要由固结系数cv控制。曲线的峰值则主要与土层深度z负相关,与固结压力p成正比。
计算不同土层深度的水力梯度最大值imax,作图6。根据量纲法和图6推导 公式如下:
(9)
式中: 为水力梯度最大值; 为无量纲参数,算例中 。
表1和表2分别列出了算例中水力梯度上升和下降两阶段Logistic函数计算公式以及各参数取值。
上升阶段令 , , , 。对表1中参数结合量纲法分析,拟合可得式(10)。

Figure 4. Schematic of physical model
图4. 物理模型示意图

Figure 5. Variation of hydraulic gradient i with time
图5. 水力梯度随时间的变化
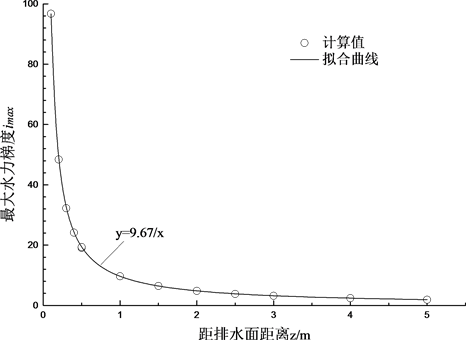
Figure 6. Variation of hydraulic gradient imax with z
图6. imax随z的变化图
Table 1. Logistic model and parameters upward
表1. 上升阶段Logistic模型及各参数取值
Table 2. Logistic model and parameters downward
表2. 下降段Logistic模型及各参数取值
(10)
式中: 为无量纲参数,算例中 。
将 、 、 、 参数值代入式(4)可得上升阶段水力梯度i的Logistic公式,见式(11)。
(11)
同理,下降阶段令 , , , ,且极值点以上升阶段极值 为主。联系表2中数据 、 和土体固结参数,结合量纲分析可得式(12)~式(14)。
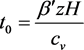 (12)
(12)
(13)
(14)
式中:
、A、B为无量纲参数(算例中
,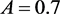 ,
)。
,
)。
综上,结合算例,一维固结水力梯度的Logistic模型可表示如下:
上升阶段:
(15)
下降阶段:
(16)
3.3. 数值模拟
采用有限元软件ABAQUS对渗流固结的模型进行模拟,土体的性质参数与算例一致,土体厚度5 m,以Terzaghi一维固结理论为基础进行有限元计算。边界条件:模型底部固定两个方向的约束,不排水;两侧仅能容许竖向位移,同样不排水;表面位移自由,且是自由排水面。施加荷载后根据土体各个时刻孔隙水压力沿深度的切线值求得水力梯度和时间的关系。模型中土体采用CPE4P单元,初始孔隙比为1.0,设置时间总长为10,000天。固结压力的施加分为瞬时加载和线性加载两种工况。
3.3.1. 瞬时加载结果分析
瞬时加载200 kPa,得到数值结果如下。图7表明距离排水面越远的位置孔压越大,即孔压消散的速度越慢。图8反映了最终的地表沉降值为68.5 cm,与理论计算值一致。图9和图10分别为水力梯度和沉降速率随时间的变化图。
图9曲线走势与解析解一致,并且与图10沉降速率变化曲线很接近。经计算沉降速率与水力梯度比值,结果表明渗流稳定后排水速率与水力梯度关系符合Darcy定律,则水力梯度的变化能预测固结过程中的沉降速率。
按照上文方法,由式(11)、(14)可求得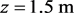 处水力梯度变化曲线的Logistic模型如下:
处水力梯度变化曲线的Logistic模型如下:
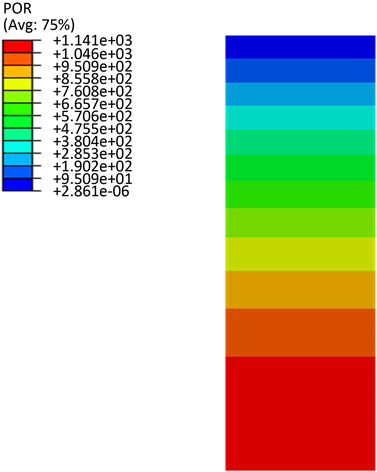
Figure 7. Distribution of pore pressure (t = 10,000 d)
图7. 孔压分布云图(t = 10,000 d)
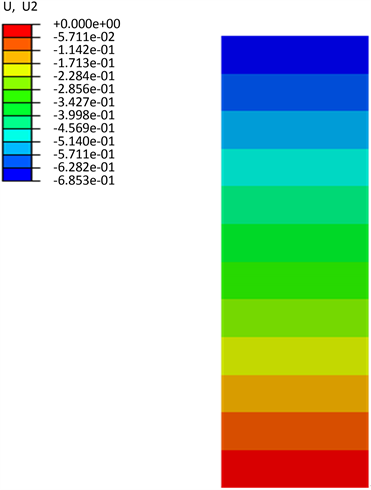
Figure 8. Distribution of settlement (t = 10,000 d)
图8. 沉降分布云图(t = 10,000 d)
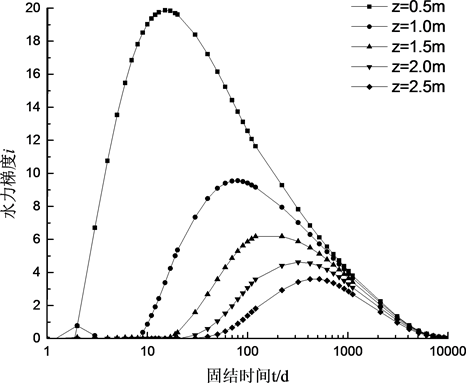
Figure 9. Distribution of settlement (t = 10,000 d)
图9. 沉降分布云图(t = 10,000 d)

Figure 10. Distribution of settlement (t = 10,000 d)
图10. 沉降分布云图(t = 10,000 d)
(17)
图11为Logistic模型与数值计算结果拟合图,最大误差在下降段2000 d左右,但在合理考虑范围。
通过数值模拟结果可证实文中所提出的水力梯度Logistic模型可行。
3.3.2. 线性加载结果分析
假定荷载在前30 d线性加载至200 kPa后保持不变,见图12。其余与瞬时加载模拟相同,计算结果见图13和图14。
比较图7和图13可知两种不同加载方式孔压终值几乎相等。图14中线性加载水力梯度变化趋势与瞬时加载一致,图15为同一深度的水力梯度值对比,发现在一定时间内线性加载水力梯度值小于瞬时加载水
力梯度值,且其差值随深度和时间的增加而减小。这主要是由于水力梯度与荷载、固结时间和深度均相关,本实例线性加载30 d内荷载小于200 kPa,故前期孔压大小及消散速率均不一致,而不同深度水力梯度变化有一定滞后性,所以距离排水面越近的土体加载初期受荷载影响较大,两种不同加载方式下的差值越大。随时间增长,两种工况下相同荷载作用时间较长,初期荷载影响变小,后期水力梯度变化比较接近。在线性加载工况下,水力梯度变化规律仍符合Logistic模型。
同理,非线性拟合后可求得 水力梯度的Logistic模型如下:
(18)
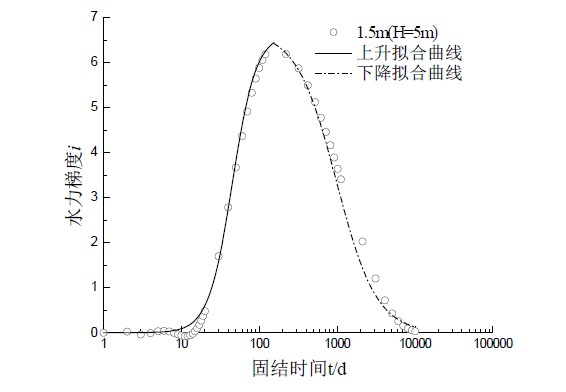
Figure 11. Comparison of ABAQUS numerical solution and formula (15)
图11. 数值计算与式(15)拟合对比图

Figure 12. Variation of linear load with time
图12. 线性加载荷载随时间变化图
4. 结论
本文基于Terzaghi一维固结解析解推导了水力梯度的Logistic模型,并采用有限元软件ABAQUS模拟得到瞬时加载和线性加载两种工况下水力梯度和固结沉降速率随时间变化曲线。研究结论如下:
1) 水力梯度在固结过程中随时间先增大后减小,其变化曲线分为上升和下降两阶段的S型曲线,且
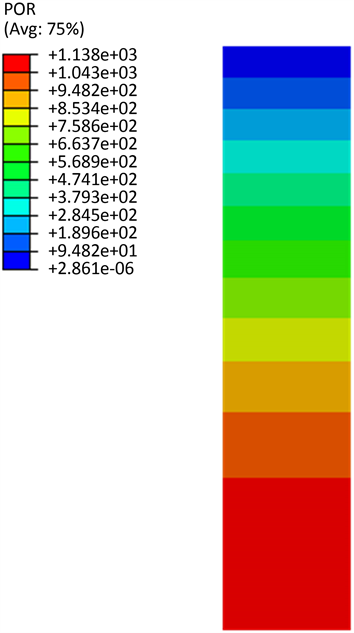
Figure 13. Distribution of pore pressure after consolidation
图13. 固结结束时模型孔压的分布
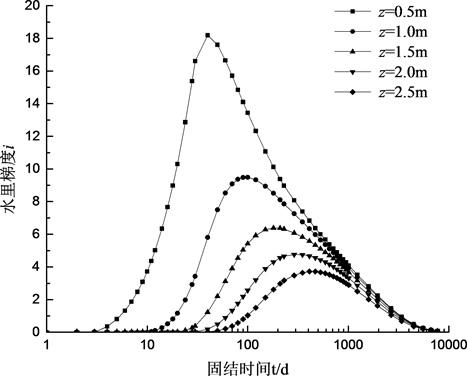
Figure 14. i-t curve of ABAQUS numerical solution
图14. 数值模拟的i-t曲线(H = 5 m)

Figure 15. i-t curve of instantaneous load and linear load
图15. 瞬时加载和线性加载i-t曲线比较图(H = 5 m)
水力梯度的变化主要是受土体本身固结参数的影响,简化Logistic函数中各参数与固结参数H、z、Cv的关系式后,可采用水力梯度的Logistic模型定量描述固结过程中水力梯度的变化规律。
2) 水力梯度的Logistic模型中,无量纲参数α、β等取值应视具体情况考虑。本文以Terzaghi一维固结解析解为基础,虽存在一定的拟合误差,但能较好反映固结过程中水力梯度的变化规律,预测固结排水速率,分析固结过程机理。
基金项目
国家自然科学基金项目(51708497);宁波市自然科学基金项目(2017A610306)。
文章引用
李金柱,兰 璐,谢新宇. Logistic模型在软黏土一维固结水力梯度预测中的应用
Research on Logistic Model of Hydraulic Gradient in One-Dimensional Consolidation of Saturated Clay[J]. 渗流力学进展, 2018, 08(02): 22-34. https://doi.org/10.12677/APF.2018.82004
参考文献
- 1. 代革联. 对水力梯度的理解及其应用分析[J]. 西北地质, 1997, 18(4): 102-105.
- 2. 陈建生, 李兴文. 堤防管涌产生集中渗漏通道机理与探测方法研究[J]. 水利学报, 2000, 9(9): 48-54.
- 3. 周健, 姚志雄. 管涌发生发展过程的细观试验研究[J]. 地下空间与工程学报, 2007, 3(5): 842-848.
- 4. 房后国, 刘娉慧. 海积软土排水固结机理分析[J]. 吉林大学学报: 地球科学版, 2005, 35(2): 207-212.
- 5. S. Hansbo. Consolidation equation valid for both Darcian and non-Darcianflow[J]. Géotechnique, 2001, 51(1):51-54. https://doi.org/10.1680/geot.2001.51.1.51
- 6. 齐添, 谢康和. 萧山粘土非达西渗流性状的试验研究[J]. 浙江大学学报, 2007, 41(6): 1023-1028.
- 7. 冯晓腊. 饱和粘性土的渗透固结特性及其微观机制的研究[J]. 水文地质工程地质, 1991, 18(1): 6-11.
- 8. 王秀艳. 对粘性土孔隙水渗流规律本质的新认识[J]. 地球学报, 2003, 24(1): 91-95.
- 9. Liu, H.H. and Jens, B. (2012) On the Relationship between Water Flux and Hydraulic Gradient for Unsaturated and Saturated Clay. Journal of Hydrology, 475, 242-247. https://doi.org/10.1016/j.jhydrol.2012.09.057
- 10. Griffiths, F.J. and Joshi, R.C. (1989) Change in Pore Size Distribution Due to Consolidation of Clays. Geotechnique, 39, 159-167. https://doi.org/10.1680/geot.1989.39.1.159
- 11. Fenton, G.A. and Griffiths, D.V. (1997) Extreme Hydraulic Gradient Statistics in Stochastic Earth Dam. Journal of Geotechnical and Geoenvironmental Engineering, 123, 995-1000. https://doi.org/10.1061/(ASCE)1090-0241(1997)123:11(995)
- 12. 黄杰卿. 非线性大应变固结理论与试验研究[D]: [博士学位论文]. 杭州: 浙江大学, 2015.
- 13. 吴健. 饱和软土复杂非线性大变形固结特性及应用研究[D]: [博士学位论文]. 杭州: 浙江大学, 2008.
- 14. 杨少丽, 齐剑峰. 桶基负压沉贯下粉土中水力梯度的变化过程[J]. 岩土工程学报, 2004, 25(6): 662-665.
- 15. 宰金珉, 梅国雄. 成长曲线在地基沉降预测中的应用[J]. 南京建筑工程学院学报(自然科学版), 2000(2): 8-13.
- 16. 梅国雄, 宰金珉. 沉降时间曲线呈“S”型的证明——从一维固结理论角度[J]. 岩土力学, 2004, 25(1): 20-22.
