Journal of Water Resources Research
Vol.05 No.06(2016), Article ID:19294,8
pages
10.12677/JWRR.2016.56062
Uncertainty Analysis of Equal Reliability Principle Based Estimation of Design Flood in the Framework of Bayesian Theory
Yiming Hu1, Zhongmin Liang2, Jing Yang2, Jun Wang2, Binquan Li2
1Research Institute of Management Science, Business School, Hohai University, Nanjing Jiangsu
2College of Hydrology and Water Resources, Hohai University, Nanjing Jiangsu

Received: Nov. 26th, 2016; accepted: Dec. 9th, 2016; published: Dec. 19th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The traditional hydrological frequency analysis depends on the assumption that the flood series should be stationary, which has been influenced by climate change and human activities. Under non-stationary conditions, how to refer the design flood with a given design standard is a hot topic. The recently proposed equal reliability method is expected to solve this problem. The equal reliability principle considers the impact of engineering lifetime on the estimation of design flood. However, more parameters need to be estimated by the equal reliability method. The uncertainty of parameter estimation unavoidably results in uncertainty of design flood. Therefore, the Bayesian theory is applied to analyze the impact of parameter uncertainty on design flood, which provides the expected values and confidence intervals of the design floods.
Keywords:Non-Stationary, Design Flood, Equivalent Reliability Method, Bayesian Theory, Uncertainty Analysis

贝叶斯框架下等可靠度法推求洪水设计值的 不确定性分析
胡义明1,梁忠民2,杨靖2,王军2,李彬权2
1河海大学商学院管理科学研究所,江苏 南京
2河海大学水文水资源学院,江苏 南京

收稿日期:2016年11月26日;录用日期:2016年12月9日;发布日期:2016年12月19日

摘 要
气候变化及人类活动的影响破坏了现行洪水频率分析方法中对洪水极值系列需满足一致性的假定。在非一致性条件下,如何推求给定设计标准下的洪水设计值是目前的研究热点及难点。“等可靠度”法是提出的一种面向非一致性洪水设计值估计的方法,其考虑了工程设计寿命对设计值估计的影响。然而,该方法中需要估计的模型参数通常较多,参数估计的不确定性不可避免地会导致洪水设计值估计的不确定性。本文应用贝叶斯理论研究“等可靠度”法推求洪水设计值时,参数估计不确定性对洪水设计值的影响。在获得设计值的期望估计(点估计)的同时,还可通过置信区间估计来定量评估设计值的不确定性。
关键词 :非一致性,洪水设计值,等可靠度法,贝叶斯理论,不确定性分析

1. 引言
在工程洪水计算中,无论是基于径流系列直接推求设计洪水,还是通过耦合设计暴雨与洪水模型的间接途径推求设计洪水,都依赖于径流/降雨的极值样本系列。现行洪水频率分析应用的前提条件是洪水极值系列要满足独立同分布假定,即一致性/平稳性假定 [1] [2] [3] [4] 。然而,由于全球气候变化及人类活动的影响,导致洪水极值系列的非一致性问题越来越突出,一般不再满足一致性假定 [5] [6] [7] [8] 。
针对非一致性的洪水极值系列,目前通常采用变参数概率分布函数接描述其分布特征,即建立概率分布函数中的参数与某些协变量(如时间、降雨等)之间的统计关系,以驱动分布函数中的参数随着协变量变化,来刻画环境变化对极值分布函数的影响。而关于协变量的选取,主要是采用时间、降雨、下垫面等指标等 [9] [10] [11] [12] 。这就导致了对于给定的一个重现期T,相应的设计值随时间是变化的,不是唯一常数,而是同时对应多个设计值。因而,在工程洪水设计中,很难选取采用哪一个设计值作为重现期T对应的设计值。2016年,梁忠民和胡义明等 [13] 提出了非一致性洪水设计值估计的“等可靠度”法。该方法基于可靠度指标,考虑了工程设计寿命对设计值估计的影响,且可降低变参数概率分布模型随时间的外延幅度。
在“等可靠度”法中,需要采用变参数概率分布函数来描述非一致性洪水极值的分布特征。在变参数概率分布函数中需要估计的参数众多,如基于三参数皮尔逊分布函数构建的变参数概率分布函数中需要估计的参数至少有4个,这就不可避免地会导致参数估计存在不确定性,进而使得基于“等可靠度”法计算的洪水设计值存在不确定性。
本文提出采用贝叶斯理论,研究在考虑参数估计不确定性条件下,“等可靠度”法计算洪水设计值的不确定性问题,以定量评估参数估计对洪水设计值估计的影响。
2. 理论方法
2.1. “等可靠度”法描述
“等可靠度”法是梁忠民和胡义明等 [13] 提出的一种非一致性条件洪水设计值估计的方法。其核心思想是:在非一致性框架下,无论环境如何变化,都应保证非一致性条件下推求的洪水设计值 对应的工程可靠度
对应的工程可靠度 应与决策人员“规划”的工程设计可靠度
应与决策人员“规划”的工程设计可靠度 一致。在非一致性条件下,决策人员只需按照一致性思维框架下的重现期概念提出其期望的工程设计标准(抗御
一致。在非一致性条件下,决策人员只需按照一致性思维框架下的重现期概念提出其期望的工程设计标准(抗御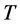 年一遇洪水)和工程的设计运行周期(
年一遇洪水)和工程的设计运行周期( 年)。因而,就可采用“等可靠度”法推求非一致性性条件下的洪水设计值
年)。因而,就可采用“等可靠度”法推求非一致性性条件下的洪水设计值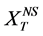 。为便于使用,可将
。为便于使用,可将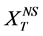 表述为非一致性条件下重现期为T年一遇的洪水设计值。进而,可度量非一致性条件下的工程洪水设计值,方便了工程决策和设计人员使用。
表述为非一致性条件下重现期为T年一遇的洪水设计值。进而,可度量非一致性条件下的工程洪水设计值,方便了工程决策和设计人员使用。
为了阐述“等可靠度”法推求给定重现期对应的洪水设计值的基本思路,现假定有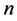 年的洪峰观测系列
年的洪峰观测系列 ,且该系列呈现减少趋势。采用基于三参数的皮尔逊分布(PE3)构建的变参数概率分布函数对洪峰系列的概率分布特征进行描述。假定分布函数的位置参数
,且该系列呈现减少趋势。采用基于三参数的皮尔逊分布(PE3)构建的变参数概率分布函数对洪峰系列的概率分布特征进行描述。假定分布函数的位置参数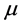 和尺度参数
和尺度参数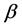 随时间变化,而尺度参数
随时间变化,而尺度参数 为常数,即
为常数,即
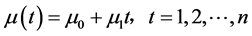 (1)
(1)
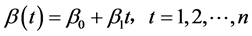 (2)
(2)
 (3)
(3)
则变参数的PE3概率密度函数可表示为
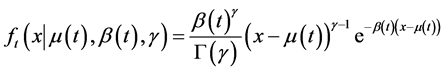 (4)
(4)
基于系列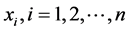 ,可获得参数
,可获得参数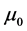 、
、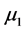 、
、 、
、 和
和 的估计值;进而获得不同年份
的估计值;进而获得不同年份 对应的变参数PE3概率分布函数,
对应的变参数PE3概率分布函数, 。
。
按照“等可靠度”的基本思想,工程设计人员只需要在一致性(现行洪水频率分析)条件下,表述其对工程的设计要求:“希望工程在L年的设计寿命周期内,可防御T年一遇的洪峰事件”。基于此表述,可计算出工程设计人员“规划”的工程设计可靠度为
 (5)
(5)
而实际上,工程在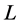 年的设计寿命期(即第
年的设计寿命期(即第 到
到 年)内,不同时刻对应的分布函数
年)内,不同时刻对应的分布函数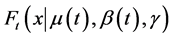 ,
, 是随时间而变化的,是不平稳的。对于给定的设计阈值
是随时间而变化的,是不平稳的。对于给定的设计阈值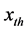 ,可计算出工程在设计寿命期
,可计算出工程在设计寿命期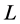 年内的可靠度为
年内的可靠度为
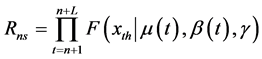 (6)
(6)
基于“等可靠度”法思想:无论环境如何变化,都应保证非一致性条件下推求的洪峰设计值对应的工程可靠度(式(6))应与“规划”的可靠度(式(5))一致,即
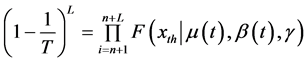 (7)
(7)
求解使式(7)成立的阈值 ,记为
,记为 ,即是非一致性条件下T年一遇的洪峰设计值。
,即是非一致性条件下T年一遇的洪峰设计值。
从上述“等可靠度”法推求洪峰设计值的基本思路可以看出,洪峰的概率分布函数在不同时刻是不同的,也即洪峰不满足“同分布”假定,但洪峰的独立性假定还是需要满足的。
2.2. 参数估计不确定性对洪水设计值的影响
以公式(1)-(4)描述的变参数PE3函数为例,该函数需要估计的系数参数为 共5个;当获得上述5个系数参数的估计值后,即可获得在不同时刻
共5个;当获得上述5个系数参数的估计值后,即可获得在不同时刻 时,PE3分布函数中的分布参数
时,PE3分布函数中的分布参数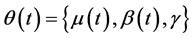 。
。 表示系数参数的先验分布。由贝叶斯理论 [14] 可获得系数参数
表示系数参数的先验分布。由贝叶斯理论 [14] 可获得系数参数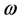 的后验概率分布函数
的后验概率分布函数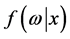 ,
,
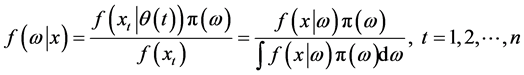 (8)
(8)
在实际应用过程中,系数参数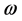 后验分布的求解通常面临高维且无解析解的情况,为此,需采用马尔科夫链蒙特卡洛(MCMC)抽样方法从后验分布
后验分布的求解通常面临高维且无解析解的情况,为此,需采用马尔科夫链蒙特卡洛(MCMC)抽样方法从后验分布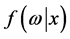 中进行大量的随机采样。在抽样过程中,假定各个系数参数是相互独立的。各个系数参数的先验分布函数可采用均匀分布或正态分布等进行刻画。假定抽取参数
中进行大量的随机采样。在抽样过程中,假定各个系数参数是相互独立的。各个系数参数的先验分布函数可采用均匀分布或正态分布等进行刻画。假定抽取参数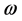 的样本数共
的样本数共 组,记为
组,记为 。参数不确定性对洪水设计值估计的影响可采用下述方案进行评估。以推求工程设计寿命为
。参数不确定性对洪水设计值估计的影响可采用下述方案进行评估。以推求工程设计寿命为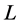 年,设计重现期为T年的洪水设计值
年,设计重现期为T年的洪水设计值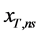 为例。
为例。
(1) 对于给定的设计重现期T和工程寿命 ,按式(5)计算工程的可靠度
,按式(5)计算工程的可靠度 :
:
(2) 从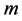 组系数参数
组系数参数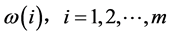 中抽取一组,记为
中抽取一组,记为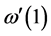 ;
;
(3) 按式(1)-(3)计算未来每个时刻t对应的分布参数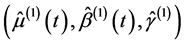 ,进而可得到每个时刻的概率分布函数
,进而可得到每个时刻的概率分布函数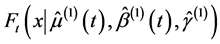 。根据“等靠度”概念,即变化环境下工程设计可靠度与一致性条件下工程的设计可靠度相等,通过式(9)计算在变化环境下,T年重现期对应的设计值
。根据“等靠度”概念,即变化环境下工程设计可靠度与一致性条件下工程的设计可靠度相等,通过式(9)计算在变化环境下,T年重现期对应的设计值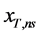 的估计值,记为
的估计值,记为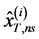 :
:
 (9)
(9)
(4) 从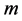 组系数参数
组系数参数 中再抽取一组,记为
中再抽取一组,记为 ,根据步骤(3),可获得T年重现期对应的设计值
,根据步骤(3),可获得T年重现期对应的设计值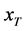 的第二个估计值
的第二个估计值 ;不断地从
;不断地从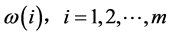 中抽取样本,并重复执行步骤(3),直到抽完第
中抽取样本,并重复执行步骤(3),直到抽完第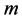 组参数
组参数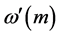 后,可获得设计值
后,可获得设计值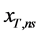 的
的 组估计值
组估计值 ;
;
(5) 将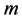 组T年重现期对应的设计值
组T年重现期对应的设计值 的估计值
的估计值 的经验分布
的经验分布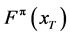 作为设计值
作为设计值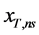 的分布,进而可计算T年重现期对应的设计值的点估计和区间估计,以定量评估模型参数不确定性对洪水设计值估计的影响。
的分布,进而可计算T年重现期对应的设计值的点估计和区间估计,以定量评估模型参数不确定性对洪水设计值估计的影响。
3. 实例研究
本节以黄龙滩站1956~2014年共59年的洪峰系列为对象,对本文所提出的不确定性分析方法进行实例研究。图1给出了黄龙滩站所在流域的位置图。图2位洪峰系列的时间序列图。从图中可以看出,该系列呈现出明显的减少性趋势。
基于PE3分布函数和广义极值分布函数(GEV),构建了4个变参数的概率分布函数直接对该洪峰系列的分布特征进行拟合。
GEV分布函数可表示如下,
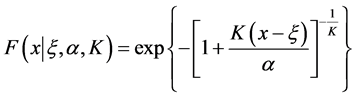 (10)
(10)
式中: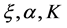 分别为位置、尺度和形状参数。构建的4个变参数概率分布模型如下:
分别为位置、尺度和形状参数。构建的4个变参数概率分布模型如下:
(1) 模型1:PE3分布函数中的位置参数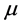 随着时间线性变化,而尺度参数
随着时间线性变化,而尺度参数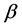 和形状参数
和形状参数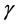 为常数。即
为常数。即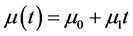 ,
, ,
,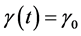 ,记为PE3-Loc。
,记为PE3-Loc。
(2) 模型2:PE3分布中位置参数 和尺度参数
和尺度参数 随时间变化,形状参数
随时间变化,形状参数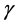 为常数。即
为常数。即 ,
,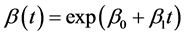 ,
,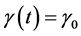 ,记为PE3-Loc-Scl。
,记为PE3-Loc-Scl。
(3) 模型3:GEV分布函数中的位置参数 随时间变化,而尺度参数
随时间变化,而尺度参数 和形状参数
和形状参数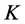 为常数。即
为常数。即 ,
, ,
,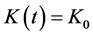 ,记为GEV-Loc。
,记为GEV-Loc。
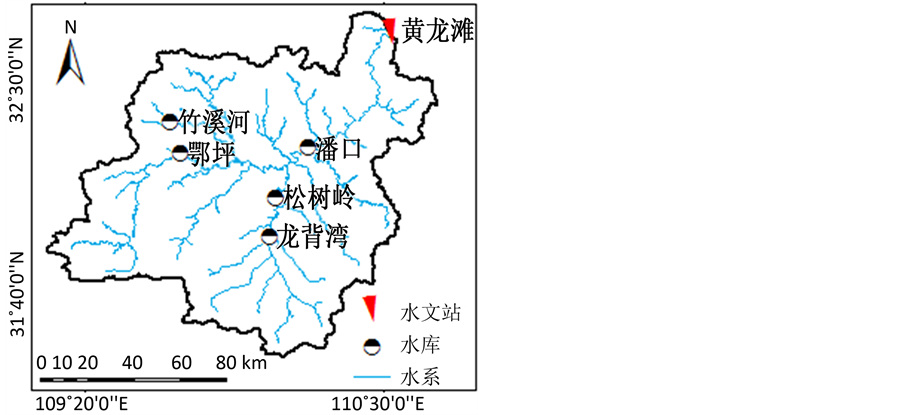
Figure 1. Location and hydrological station at the Huanglongtan basin
图1. 黄龙滩水文站点及流域位置

Figure 2. Time series of peak flow
图2. 洪峰系列的时间序列图
(4) 模型4:GEV分布函数中位置参数 和尺度参
和尺度参 数随时间变化,而形状参数
数随时间变化,而形状参数 为常数。即
为常数。即 ,
,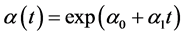 ,
,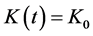 ,记为GEV-Loc-Scl。
,记为GEV-Loc-Scl。
对于模型参数的估计,采用了2.2节所述的贝叶斯方法,并通过MCMC法从参数的后验分布中进行大量采样。在抽样过程中,平行运行5条链,每条链上采取10000个样本(此时每条链都已收敛),去掉预热的9000个样本,每条链上仅采用最后的1000个样本,5条链共计5000个样本值,其中使参数后验密度值达到最大的即参数的最大后验估计。基于最大后验估计参数计算了AIC和BIC指标,用以评估4个不同的概率分布函数模型对洪峰系列的拟合效果,见表1。
从表中可以看出,第二个模型(PE3-Loc-Scl模型)的AIC和BIC值最小,即PE3-Loc-Scl为最优模型。
图3给出了PE3-Loc-Scl模型拟合洪峰系列时,重现期为10年、20年、50年和100年条件下,对应的设计值随时间的演变特征。
从图中可以看出,不同重现期条件下的设计值都随时间在不断减少,这与洪峰系列呈减少趋势相吻合。59
Table 1. AIC and BIC for assessing the model performance
表1. 不同模型对洪峰系列拟合的指标值
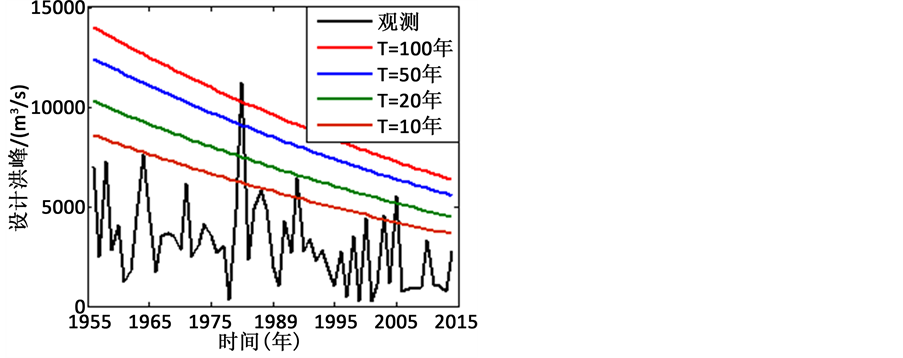
Figure 3. The designed peak flow with different return periods for PE3-Loc-Scl model
图3. PE3-Loc-Scl模型拟合洪峰设计值随时间演变特征
年的实际观测系列中,超过10年、20年、50年和100年一遇的洪峰发生次数分别为6次、3次、1次和1次。总体来说,该模型的拟合结果与实际观测较为符合。
基于2.2节所述方法,获得不同工程设计寿命条件下设计值的分布,并计算了给定重现期对应设计值的期望估计和90%置信区间估计。图4给出了工程设计寿命为40年、50年、60年、80年和100年条件下,10年、20年、50年和100年重现期对应的设计值的期望估计和90%置信区间估计。从图中可以看出,随着工程设计寿命的增加,不同重现期对应的设计值的期望估计均随着设计寿命的增加而减少。这与该洪峰系列呈现减少趋势相一致。在给定工程设计寿命条件下,设计值的90%置信区间宽度(即不确定性)随着重现期的增大而增加,也即推求大重现期设计洪水时通常存在更大的确定性。在给定重现期条件下,设计值的90%置信区间的宽度(即不确定性)随着工程设计寿命的增加而增加。这表明在变化环境下,变参数概率分布函数模型外延时间越长,模型计算的结果也将可能会存在较大不确定性。
4. 结论
考虑到应用“等可靠度”法计算洪水设计值时,参数估计不确定性对洪水设计值的影响,本文提出了采用贝叶斯方法来定量评估参数估计对洪水设计值的不确定性影响,并基于黄龙滩站的洪峰极值系列样本,对本文所提方法进行了示例研究。
示例研究结果表明,(1) 在给定工程设计寿命条件下,设计值的不确定性随着重现期的增大而增加,也即推求大重现期设计洪水时通常存在更大的不确定性;(2) 在给定重现期条件下,设计值的不确定性随着工程设计寿命的增加而增加,这表明在变化环境下,变参数概率分布函数模型外延时间越长,模型计算的结果也将可能会存在较大不确定性。
本文中,概率分布函数的参数仅是随时间因子变化,而没有考虑其它因子的影响。另外,仅提出了考虑参
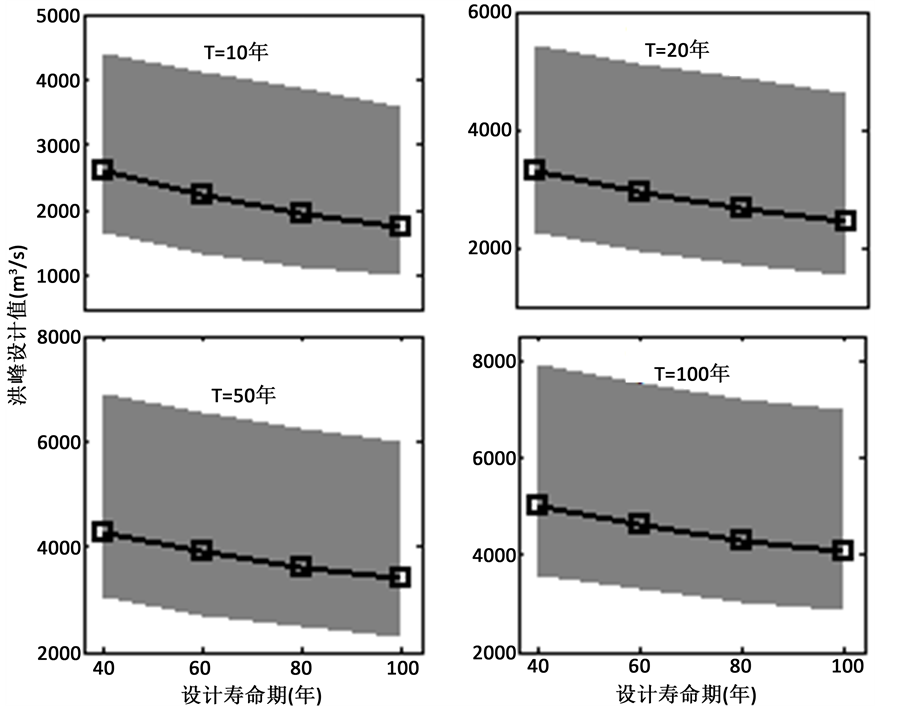
Figure 4. The 90% confident interval of 15-day flood design value with different return periods under the conditions of different engineering lifetimes
图4. 不同工程设计寿命及重现期下洪峰设计值的期望估计和90%置信区间估计
数估计不确定性条件下,“等可靠度”法推求设计值情况下设计值的不确定性评估。关于分布函数选取等不确定对设计值的影响分析,将在以后的工作中进一步深入研究。
基金项目
国家自然科学基金重大项目(51190095)。
文章引用
胡义明,梁忠民,杨 靖,王 军,李彬权. 贝叶斯框架下等可靠度法推求洪水设计值的不确定性分析
Uncertainty Analysis of Equal Reliability Principle Based Estimation of Design Flood in the Framework of Bayesian Theory[J]. 水资源研究, 2016, 05(06): 530-537. http://dx.doi.org/10.12677/JWRR.2016.56062
参考文献 (References)
- 1. MILLY, P. C. D., BETANCOURT, J., FALKENMARK, M., et al. Stationary is dead: whither water management. Science, 2009, 319(5863): 573-574. https://doi.org/10.1126/science.1151915
- 2. 梁忠民, 胡义明, 王军. 非一致性洪水频率分析的研究进展[J]. 水科学进展, 2011, 22(6): 145-152. LIANG Zhongmin, HU Yiming and WANG Jun. Advances in hydrological frequency analysis of non-stationary time series. Advance in Water Science, 2011, 22(6): 864-871. (in Chinese)
- 3. 郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价[J]. 水利学报, 2016, 47(3): 51-64. GUO Shenglian, LIU Zhangjun and XIONG Lihua. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 51-64. (in Chinese)
- 4. 熊立华, 江聪, 杜涛, 等. 变化环境下非一致性洪水频率分析研究综述[J]. 水资源研究, 2015, 4(4): 310-319. XIONG Lihua, JIANG Cong, DU Tao, et al. Review on nonstationary hydrological frequency analysis under changing envi-ronments. Journal of Water Resources Research, 2015, 4(4): 310-319. (in Chinese)
- 5. 谢平, 陈广才, 夏军. 变化环境下非一致性年径流系列的洪水频率计算原理[J]. 武汉大学学报(工学版), 2005, 38(6): 6-9. XIE Ping, CHEN Guangcai and XIA Jun. Hydrological frequency calculation principle of inconsistent annual runoff series under changing environments. Engineering Journal of Wuhan University, 2005, 38(6): 6-9. (in Chinese)
- 6. 冯平, 曾杭, 李新. 混合分布在非一致性洪水频率分析的应用[J]. 天津大学学报: 自然科学与工程技术版, 2013, 46(4): 298-303. FENG Ping, ZENG Hang and LI Xin. Non-stationary flood-frequency analysis based on mixed distribution. Journal of Tianjin University, 2013, 46(4): 298-303. (in Chinese)
- 7. 胡义明, 梁忠民, 杨好周, 陈东初. 基于趋势分析的非一致性洪水频率分析方法研究[J]. 水力发电学报, 2013, 31(5): 21-25. HU Yiming, LIANG Zhongmin, YANG Haozhou, CHEN Dongchu. Study on frequency analysis method of non-stationary ob-servation series based on trend analysis. Journal of Hydroelectric Engineering, 2013, 31(5): 21-25. (in Chinese)
- 8. 胡义明, 梁忠民, 赵卫民, 刘晓伟. 基于跳跃性诊断的非一致性水文频率分析[J].人民黄河, 2014, 36(6): 51-53. HU Yiming, LIANG Zhongmin, ZHAO Weimin and LIU Xiaowei. Study on frequency analysis method of non-stationary ob-servation based on JUMP Analysis. Yellow River, 2014, 36(6): 51-53.
- 9. STRUPCZEWSKI, W. G., SINGH, V. P. and FELUCH, W. Non-stationary approach to at-site flood frequency modeling maximum likelihood estimation. Journal of Hydrology, 2001, 248(1-4): 123-142. https://doi.org/10.1016/S0022-1694(01)00397-3
- 10. DU, T., XIONG, L. H., XU, C. Y., et al. Return period and risk analysis of nonstationary low- flow series under climate change. Journal of Hydrology, 2015(527): 234-250. https://doi.org/10.1016/j.jhydrol.2015.04.041
- 11. 叶长青, 陈晓宏, 张家鸣, 朱爱萍, 张丽娟. 具有趋势变异的非一致性东江流域洪水序列频率计算研究[J]. 自然资源学报, 2013, 28(12): 2105-2116. YE Changqing, CHEN Xiaohong, ZHANG Jiaming, ZHU Aiping and ZHANG Lijuan. Methods of hydrological frequency analysis for nonstationary flood data with trend components in Dongjiang River Basin. Journal of Natural Resources, 2013, 28(12): 2105-2116. (in Chinese)
- 12. SINGH, V. P., WANG, S. X. and ZHANG, L. Frequency analysis of nonidentically dis-tributed hydrologic flood data. Journal of Hydrology, 2005, 307(1-4): 175-195. https://doi.org/10.1016/j.jhydrol.2004.10.029
- 13. 梁忠民, 胡义明, 黄华平, 王军, 李彬权. 非一致性条件下洪水设计值估计方法探讨[J]. 南水北调与水利科技, 2016, 14(1): 52-56. LIANG Zhongmin, HU Yiming, HUANG Huaping, WANG Jun and LI Binquan. Study on the estimation of design value under non-stationary environment. South to North Water Transfers and Water Science & Technology, 2016, 14(1): 52-56. (in Chi-nese)
- 14. LIANG, Z. M., CHANG, W. J. and LI B. Q. Bayesian flood frequency analysis in the light of model and parameter uncertainties. Stochastic Environmental Research and Risk Assessment, 2012, 26(5): 721-730. https://doi.org/10.1007/s00477-011-0552-y
