Modeling and Simulation
Vol.
08
No.
04
(
2019
), Article ID:
32580
,
9
pages
10.12677/MOS.2019.84017
Simulation Analysis for an Electrical Vehicle HVAC Assembly
Xinda Zhu, Lin Su, Kang Li, Yidong Fang, Hao Gao, Mingkang Liu
School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai
Received: Sep. 30th, 2019; accepted: Oct. 14th, 2019; published: Oct. 21st, 2019

ABSTRACT
In order to study structural characteristics of an electrical vehicle HVAC (Heating, ventilation and air conditioning) assembly, the modal analysis, vibration analysis and static analysis of an electrical vehicle HVAC assembly are carried out by using the finite element numerical simulation method. According to the analysis results, the optimization measures are put forward. In modal analysis, results show the fundamental natural frequency (143 Hz) of HVAC assembly is above the external excitation frequency range of 30~100 Hz during actual operations, and resonances can be avoided. In the analysis of natural vibration characteristics, results show the structure of the HVAC assembly has high fundamental frequency and good stiffness. In static analysis, results show the maximum stress value (5.467 Mpa) is far less than the tensile strength of the material, and the installation reliability is high for this automobile HVAC assembly.
Keywords:Electrical Vehicle HVAC Assembly, Modal Analysis, Natural Frequency, Static Analysis, Tensile Strength
某电动汽车空调HVAC总成的仿真分析
朱信达,苏林,李康,方奕栋,高浩,刘明康
上海理工大学,能源与动力工程学院,上海
收稿日期:2019年9月30日;录用日期:2019年10月14日;发布日期:2019年10月21日

摘 要
本文为了研究某电动汽车空调HVAC总成的结构特性,采用有限元数值模拟的方法,分别对HVAC总成进行了模态分析、振动特性分析和静力分析,并根据分析结果提出了优化措施。结果表明:模态分析中,HVAC总成的一阶固有频率(143 Hz)避开了实际运行过程中的外界激励频率(30~100 Hz),不会发生共振;自振特性分析中,HVAC总成结构基频高,刚度好;静力分析中,最大应力值(5.467 Mpa)远小于材料的拉伸强度,因此该HVAC总成的安装可靠性高。
关键词 :电动汽车HVAC总成,模态分析,固有频率,静力分析,拉伸强度

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着能源的紧缺和环境污染问题的日益严峻,研发新能源汽车已经成为当今汽车领域的热点 [1] [2]。传统的燃油车采用的是发动机余热供暖,而本文研究的对象是某款电动汽车空调的HVAC总成。不同于传统燃油车由发动机提供动力,电动汽车采用电池驱动,在冬季无法利用发动机余热对乘员舱进行供暖,本款电动汽车采用热泵系统进行供暖并添加一小型PTC进行辅助供暖,因此与传统的燃油车在HVAC总成的结构方面存在差异 [3]。但和传统车相同的是,电动汽车空调HVAC总成也存在振动问题,且HVAC总成的固有属性必然会对空调系统的性能及用户的舒适性产生重要影响 [4]。
李秋芳 [5] 应用有限元软件研究了汽车变速箱箱体的固有频率及振型,找出发生振动较大的区域,从理论上分析了变速箱箱体产生振动的敏感部位。董相龙等 [6] 采用有限元分析的方法计算了某型号电动汽车在急转弯和急刹车两种工况下,电池箱局部产生的应力集中现象,并根据计算结果提出改进设计。代颖等 [7] 通过有限元仿真得到电机各阶模态频率和模态振型。王世栋等 [8] 通过软件模拟,根据模态振型找出了振型最敏感的区域,提出了在此区域增加肋板的优化措施。张亚飞等 [9] [10] [11] 应用有限元分析法模拟并找出了汽车在各种实际运行工况下的车身结构的模态振型及应力分布,为车身结构优化设计提供参考。李鹏等 [12] 通过试验模态分析和计算模态分析进行比对,验证模态分析方法得出的HVAC壳体机械结构的固有振动特性的准确性。刘敏、庞剑等 [13] [14] 指出空调压缩机安装支架在A/C OFF时,主要受到汽车发动机为震源传递的振动;在A/C ON时,还附加有空调压缩机以及鼓风机带来的振动一般空调压缩机及鼓风机的各个档位(一般四档位)频率为30~100 Hz,因此,空调压缩机安装支架的固有频率应当避开这些频率范围,才能长期稳定、有效、安全地工作。Yook等 [15] 通过有限元分析和实验评估研究了由传统汽车的空调箱箱体表面的加强筋和表面刚度引起的动态特性的变化。分析目前国内外研究成果可知,关于汽车方面的模态和静力分析主要集中于变速箱、车身结构、电池箱、电机等方面,而对汽车空调HVAC总成的有限元分析未积极展开,尤其是电动汽车。因此本文通过有限元分析,展开了对某款电动汽车空调HVAC总成结构合理性的探究。
2. 汽车空调HVAC总成有限元建模
2.1. 三维数学模型的建立
在三维CAD软件中进行建模,由于不可能使模型的质量矩阵和刚度矩阵完全与实际一致,需根据等效原理对结构进行简化处理。又由于实际加工的需要,电动汽车HVAC总成被分为上壳体和下壳体,上下壳体之间通过螺栓连接,所以在进行有限元分析时把HVAC总成的上下壳体通过约束绑定在一起,当作一个整体考虑。而HVAC总成通过分布在表面的5个安装脚与整车进行固定。图1为建好的电动汽车HVAC总成的三维数学模型。
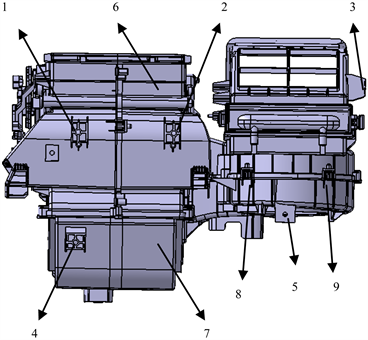 1、2、3、4、5 安装脚;6 上壳体;7 下壳体;8、9 螺栓
1、2、3、4、5 安装脚;6 上壳体;7 下壳体;8、9 螺栓
Figure 1. 3D model of HVAC assembly for electrical vehicle
图1. 电动汽车HVAC总成的三维数模
2.2. 网格划分
由于汽车HVAC总成结构的复杂性,HVAC总成表面有加强筋和安装脚。根据已经建好的几何模型,利用网格划分软件做进一步的前处理并划分网格,对一些易振区域和静力集中区域进行网格加密处理,最后修改网格尺寸。为了计算速度和精度,选用的有限元网格模型如图2。网格单元采用四面体网格,单元尺寸3 mm,节点增长率为1.1。共划分约四百万个网格,节点数为九十万个。

Figure 2. FEA model of HVAC assembly for electrical vehicle
图2. 电动汽车HVAC总成的有限元模型
2.3. 定义材料
HVAC总成的材料为PPA + 33% GF (加了33%玻纤的PPA塑料),其性能参数如表1所示:
Table 1. Performance parameter of material
表1. 材料性能参数
3. 汽车空调HVAC总成的有限元模型求解
3.1. 模态分析的理论基础
汽车HVAC总成作为连续弹性体考虑要用无限多个自由度来描述其动力学状态,即多自由度系统 [16],这个系统的振动微分方程为:
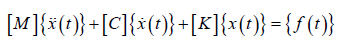 (1)
(1)
式中: ——质量矩阵, ;
——阻尼矩阵, ;
——刚度矩阵, ;
、 、 ——N维位移、速度、加速度响应变量;
——N维激励力向量。
由于其阻尼比很小,在研究HVAC总成结构的固有特性时,阻尼比对汽车HVAC总成的振型和模态分析的影响可以忽略。因此可将汽车HVAC总成结构看作是无阻尼振动,故振动微分方程可简化:
(2)
方程(2)是一个常系数齐次常微分方程,它的解即特征值和特征向量反映了结构的固有特性。
解的形式为:
(3)
式(3)中 是向量 的频率,代入式(2),可以推出
(4)
式(4)有非零解的条件是
(5)
求解式(5)可以得到第i阶频率 ,然后将求得的 代入式(4)推出第i阶的特征向量 。对特征向量进行正则化处理,即
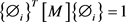 (6)
(6)
通过求出的特向量再对应求出HVAC总成的固有频率。
本文中,模态分析是为了确认电动汽车HVAC总成每一阶模态具有的固有频率和模态振型等动力特性,从而为HVAC总成结构的评估及结构设计优化奠定理论基础 [17]。其中,分析主要目的是比较HVAC总成的低阶频率和汽车运行过程中受到的外界激励力频率,避免出现共振这种对结构不利的振型,达到消除过度振动和噪声的目的。刘敏、庞剑等指出在整个汽车结构中,汽车HVAC总成受到的外界激励主要来自两个方面,一是汽车发动机的怠速频率对应的激励,其怠速激振频率为25~28 Hz,二是来源于空调压缩机和鼓风机,其频率为30~100 Hz。由于本文的研究对象是电动汽车的HVAC总成,因此主要的外界激励来源是空调压缩机和鼓风机,而结构的响应往往取决于相对较低的几阶模态。
3.2. 模态计算结果分析
本文利用三维有限元软件对电动汽车HVAC总成进行模态数值计算,得到的前四阶固有频率如表2所示。由表2可以看出,随着模态阶数的增加,固有频率也在增加。因随着模态阶数的提高,激发高阶振动的载荷能量减弱 [18]。并且随着模态阶数不同,汽车HVAC总成受到激励的节点位置也不同,所以前四阶出现了不同形式的振动。
Table 2. Natural frequencies of the first four orders
表2. 前四阶的固有频率
图3为汽车HVAC总成前4阶的模态振型图。
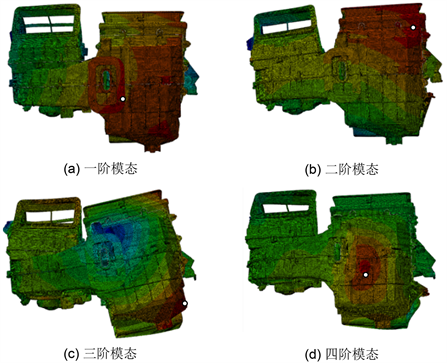
Figure 3. Order mode of vibration
图3. 模态振型图
由图3汽车HVAC总成的前四阶振型图可以看出,对于该结构,当外界激励频率达到汽车HVAC总成的固有频率时,HVAC总成的结构会发生共振现象,最终导致结构的破损和变形。对于电动汽车,由于主要激励频率是30~100 Hz,而该汽车HVAC总成结构的一阶固有频率是143 Hz,有效避开了激励频率,不会发生共振。为了进一步评估HVAC总成的可靠性,这就需要对局部位移较大的节点位置进行分析。图4是前四阶模态振型图中位移最大的四个节点45542, 26300, 46137, 74602 (节点位置如图3白点所示)前20阶模态下的位移曲线。其中(a)是一阶模态中位移最大的节点45542随模态变化的位移曲线;(b)是二阶模态中位移最大的节点26300随模态变化的位移曲线;(c)是三阶模态中位移最大的节点46137随模态变化的位移曲线;(d)是四阶模态中位移最大的节点74602随模态变化的位移曲线。由图4可以看出在发生共振的情形下,随着模态阶数的提高,各节点位移的变化趋势大致相同,即位移都随着模态阶数的提高而减少,且存在峰值。本文采用的是基于位移归一理论的有限元分析软件,结构模态的最大位移标定为1。由(a)可知其最大位移为0.96;由(b)可知位移最大为0.98;(c)中位移最大值为0.98;由(d) 可知该点的最大位移为0.97。以上四个点的最大位移都接近于最大位移1,将导致结构的破坏。而选取的几个节点对象位置大多数集中于HVAC总成的下壳体,因此可以把下壳体材料换成一种刚度更好的材料或者在下壳体增加安装脚,以提高稳定性。因此需要进一步评估材料的特性。

Figure 4. Displacement curve of node 45542, 26300, 46137, 74602
图4. 节点45542, 26300, 46137, 74602的位移曲线
3.3. 自振特性分析
结构自振特性可以反映出结构刚度 [19],从而为结构优化提供参考。为了分析的准确性和计算速度,本文提取了电动汽车HVAC总成的前20阶的固有频率,作出了图5所示的散点图。
由图可知,该结构的基频较高,且频率分布稀散,说明该结构刚度较好。因此,合理的优化方案是在下壳体位移较大的区域增加安装脚。
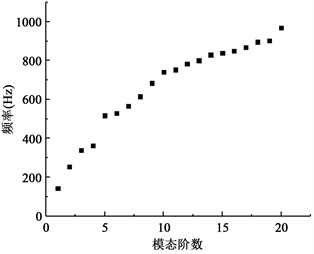
Figure 5. Frequency distribution
图5. 频率分布
3.4. 静力分析
线性分析计算结构在固定不变的载荷作用下的响应,它不考虑惯性和阻尼的影响,也不考虑载荷随时间的变化,它是一种假设,忽略载荷和结构的响应随时间的变化 [20]。因此,线性分析可以用来研究那些固定不变的惯性载荷(如重力和离心力)。考虑到本款汽车在电动机通电瞬间g值达到0.5,之后一直维持在0.3附近,而当汽车在颠簸路段运行时,实际受到的载荷可达3 g,因此,本文分别从x、y、z三个方向对汽车HVAC总成施加0.5到3倍的重力加速度,箱体周边5个螺栓孔采用固定约束,以此来模拟汽车加速、减速、颠簸和横移等实际情况,根据计算的结果分析HVAC总成是否产生应力集中、形变甚至断裂等情形。又只要最大载荷即3 g的重力加速度下的应力值在允许的范围内,则HVAC总成就能满足使用需求,所以本文只选取了汽车HVAC总成x、y、z方向受到3倍重力加速度时的应力分布云图,如图6所示。
 x轴方向施加3倍重力加速度下的应力云图
x轴方向施加3倍重力加速度下的应力云图
 y轴方向施加3倍重力加速度下的应力云图
y轴方向施加3倍重力加速度下的应力云图 z轴方向施加3倍重力加速度下的应力云图
z轴方向施加3倍重力加速度下的应力云图
Figure 6. Stress contour plot
图6. 应力云图
由图6可以看出,从x、y、z三个方向对HVAC总成施加载荷,应力均主要集中在安装脚,且明显大于其余位置受到的应力。当沿着z方向施加3倍重力加速度时,该汽车HVAC总成安装脚受到的应力值最大,不过其应力值为5.467 MPa,远小于材料的拉伸强度,因此在实际过程中不会出现断裂、破损等情况,能满足使用要求。另外,从x、y两个方向施加3倍重力加速度,该汽车HVAC总成受到的最大应力值分别为2.335 MPa和2.168 MPa,也都小于PPA + 33% GF材料的拉伸强度。图7是HVAC总成在x、y、z三个方向受到的最大值随施加的载荷变化的曲线图。
由图7可知,该汽车HVAC总成受到的最大应力值随着施加载荷的变化呈线性变化趋势,且载荷越大,最大应力值也越大。当x、y、z三个方向在相同大小的载荷作用下,z方向受到的最大应力值明显高于x、y方向受到的应力。这是因为汽车在运行过程中,x、y方向的载荷主要由汽车加减速后或横移引起,而z方向主要由于汽车在经过深坑或不平整路面颠簸引起的。
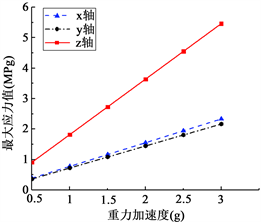
Figure 7. Maximum stress and acceleration curves
图7. 最大应力值与重力加速值的变化曲线
4. 结论
通过对某款电动汽车空调HVAC总成实际运行条件下的有限元仿真分析,主要包括模态分析、自振特性分析以及静力分析,结论如下:
1) 在模态分析中,提取了该汽车HVAC总成的前20阶固有频率,着重分析了容易促使HVAC总成共振的低阶固有频率(前4阶),该结构错开了外界激励频率(30~100 Hz),且节点的位移响应随着模态阶数的提高,峰值数量在减少,稳定性提高。因此不会发生共振,满足使用要求。
2) 在自振特性分析中,由前20阶的频率分布散点图可知该结构基频高,结构刚度好。
3) 在静力分析中,该汽车HVAC总成受到的最大应力值随着施加载荷的变化呈线性变化趋势。汽车在运行过程中,x、y方向的载荷主要由汽车加减速后或横移引起,而z方向主要由于汽车在经过深坑或不平整路面引起颠簸,所以z方向受到的最大应力值明显高于x、y方向受到的应力,但三个方向受到的最大应力值(5.467 MPa)均远小于PPA + 33% GF材料允许的最大拉伸强度,符合设计要求。
文章引用
朱信达,苏 林,李 康,方奕栋,高 浩,刘明康. 某电动汽车空调HVAC总成的仿真分析
Simulation Analysis for an Electrical Vehicle HVAC Assembly[J]. 建模与仿真, 2019, 08(04): 146-154. https://doi.org/10.12677/MOS.2019.84017
参考文献
- 1. 曹秉刚, 张传伟, 白志峰, 等. 电动汽车技术进展和发展趋势[J]. 西安交通大学学报, 2004, 38(1): 1-5.
- 2. 王文伟, 毕荣华. 电动汽车技术基础[M]. 北京: 机械工业出版社, 2010.
- 3. Zhang, Z.-Y., Wang, J.-Y., Xu, F., et al. (2018) The Solutions to Electric Vehicle Air Conditioning Systems. A Review. Renewable and Sustainable Energy Reviews, 91, 443-463. https://doi.org/10.1016/j.rser.2018.04.005
- 4. 刘敏, 李春楠, 左孔天, 等. 汽车空调压缩机支架模态与动刚度分析[J]. 客车技术与研究, 2014(2): 13-15.
- 5. 李秋芳. 基于Abaqus下的格特拉克变速箱箱体模态分析[J]. 机械工程师, 2019, 331(1): 47-49.
- 6. 董相龙, 张维强. 电动汽车电池箱结构强度的有限元分析及其改进设计[J]. 机械强度, 2015, 37(2): 312-316.
- 7. 代颖, 崔淑梅, 宋立伟, 等. 车用电机的有限元模态分析[J]. 中国电机工程学报, 2011, 31(9): 100-104.
- 8. 王世栋, 苏欣, 刘义虎, 等. 齿轮箱振动噪声仿真分析与结构优化[J]. 热能动力工程, 2019, 34(1): 92-97.
- 9. 张亚飞. 客车车身结构模态分析[J]. 汽车实用技术, 2018(18): 74-75, 86.
- 10. 沈浩, 陈昌明, 雷雨成, 等. 客车车身模态分析及评价[J]. 公路交通科技, 2003, 20(2): 128-130.
- 11. 曹文钢, 李辉, 陈维, 等. 客车车身强度与刚度的有限元分析[J]. 农业机械学报, 2007, 38(3): 39-43.
- 12. 李鹏. 某HVAC壳体自由模态分析方法探究[C]//河南省科学技术协会. 第十四届河南省汽车工程科技学术研讨会论文集. 濮阳. 2017: 161-163.
- 13. 庞剑, 谌刚, 何华, 等. 汽车噪声与振动-理论与应用[M]. 北京: 北京理工大学出版社, 2006.
- 14. 李政. 奥托汽车变速箱箱体有限元模态分析[J]. 机械传动, 2008, 32(4): 76-78, 119.
- 15. Yook, J.-Y., Cha, Y.-K., Lim, J.-S., et al. (2009) Dynamic Analysis of HVAC Case for Passenger Car. Transactions of the Korean Society for Noise and Vibration Engineering, 19, 101-108. https://doi.org/10.5050/KSNVN.2009.19.1.101
- 16. 黄海明, 郭然. 计算固体力学[M]. 北京: 科学出版社, 2014.
- 17. 帅智浩, 严海, 曹小娟, 等. 高空投送载体组合结构模态分析[J]. 鱼雷技术, 2015, 23(2): 81-85.
- 18. 田俊龙, 张翠平, 刘文坤, 等. 柴油机曲轴扭振多体动力学分析与研究[J]. 现代制造工程, 2017(10): 96-101.
- 19. 冯智颖. 柔性摩天轮结构有限元分析[J]. 中国水运, 2018, 18(12): 94-95, 98.
- 20. 江兵, 陈红, 陈丽娟, 等. 弓字形单晶梯形压电悬臂梁压电性能分析[J]. 计算机技术与发展, 2014, 24(10): 206-210.
