Statistical and Application
Vol.3 No.04(2014), Article
ID:14462,7
pages
DOI:10.12677/SA.2014.34018
Analyzing the Score Data of Five Wine Samples from Two Groups of Experts Based on R Software
Department of Statistics and Actuarial Science, College of Mathematics and Statistics, Chongqing University, Chongqing
Email: 373806737@qq.com, robertzhang@cqu.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Sep. 7th, 2014; revised: Oct. 6th, 2014; accepted: Oct. 15th, 2014
ABSTRACT
By using R software, we discuss the evaluations of five wine samples by two groups of specialists and the rationality of the evaluations. First of all, by using the hypothesis testing of two normal population means, we judge whether there are significant score differences between two groups of specialists. The test results show consistency of scores of two groups of specialists, and thus the evaluation result has certain fairness and rationality. Secondly, by using multiple t test of the mean, we can investigate the degree of differentiation of different samples by the specialists. Under the significance level of 0.05, the specialists can separate sample 1 from samples 2, 3, and 5, samples 2 and 4, samples 3 and 4. By ordering the levels of five samples from high to low, we find that the specialists can basically distinguish samples with levels with level difference by 1. But specialists do not effectively distinguish samples 1 and 4 (level difference 1.5), samples 3 and 5 (level difference 1). Then we use the hierarchical clustering method to classify five samples to three classes: excellent, good, and bad. Finally, by using the distance discriminant analysis method, the discriminant function is established based on the training sample, then by discrimination of the training sample, we get specialists’ misjudgment rate and accurate rate, and thus we can use the discriminant function to classify the new samples.
Keywords:R Software, Specialists Evaluation, Hypothesis Testing of Two Normal Populations’ Mean and Variance, Multiple t Test of the Mean, Hierarchical Clustering Method and Distance Discriminant Analysis Method

基于R软件分析两组专家对五个葡萄酒样品的评分数据
明 鹤,张应应
重庆大学,数学与统计学院,统计与精算学系,重庆
Email: 373806737@qq.com, robertzhang@cqu.edu.cn
收稿日期:2014年9月7日;修回日期:2014年10月6日;录用日期:2014年10月15日

摘 要
本文利用R软件主要讨论了两组专家对五个葡萄酒样品的评分及专家评分的合理性问题。首先,利用两个正态总体均值的假设检验评判两组专家的评分之间是否存在显著差异,从检验结果发现两组专家的评分是基本相符的,从而评比结果有一定的公平性与合理性。其次,利用均值的多重检验考察专家们对不同样品的区分度。在0.05的显著性水平下,专家们能够区分样品1与样品2、样品3、样品5,样品2与样品4,样品3与样品4。对五个样品的等级从高到低排序之后发现,专家们基本上可以区分等级相差为1的样品。但是专家们没有有效地区分出样品1与样品4(等级相差1.5),样品3与样品5(等级相差1)。然后,运用系统聚类的方法将五个样品分为优、良、差三类。最后,采用距离判别分析法,利用训练样本建立判别函数,将训练样本回代进行判别,得到专家的误判率和正确率,从而利用判别函数对新的样本进行分类。
关键词
R软件,专家评分,两个正态总体均值及方差的假设检验,均值的多重t检验,系统聚类分析和距离判别分析

1. 引言
1.1. 问题提出
目前,上至大型娱乐节目下至一般市场调查,都盛行着综合多人组成的多个小组的不同评分得出最终评价的过程,类似于选秀节目中综合专家方阵打分及大众评审打分机制。多人组成的多个小组评分机制俨然成为目前最受欢迎的评比方式,不同评分小组评分标准的差异引起的对公平公正的质疑成为活动主办方及一般观众都十分关心的问题。
1.2. 问题分析
在不确定一组样品的品质时可以通过聘请两组有资质的专家进行评分,综合两组专家的评分得出最终评价。每个专家对样品进行考察后对其各项指标打分,通过一定的汇总整理得到小组总评,再对小组的总评进行综合考虑。本文即在此背景下讨论以下三个问题:
1) 根据数据比较两组专家评分结果的差异性。
2) 专家评分能否有效地区分不同样品。
3) 根据数据分析专家评分与样品品质间的关系。
2. 实证分析
2.1. 数据分析
本文采用R软件[1] 进行计算。本文的数据为两组专家对同一系列葡萄酒的五个样品的各项指标的评分数据。两组专家各10位,他们对样品的打分主要从外观、质感、耐用性以及整体评价四个方面入手,每一个方面都有细分,外观需要对亮度和色彩打分,而质感需要从对比度、光泽度和重量打分,耐用性需要对耐磨性、耐摔性、防水性以及保修进行评分。样品等级与各项指标之间的关系可表示为图1。
2.2. 方差及均值的假设检验[2] [3]
针对两组专家评分标准不同带来的结果可靠性的质疑,我们选择假设检验的方法来考察两组评分之间的差异性。我们假定两组数据来自不同的正态总体,在此基础上考虑均值及方差是否一致。两个总体的方差一般使用 分布进行检验,在均值已知或未知情况下检验统计量有差别。同样,均值的假设检验一般使用
分布进行检验,在均值已知或未知情况下检验统计量有差别。同样,均值的假设检验一般使用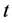 分布,在方差已知或未知时统计量也有差异。我们的验证步骤为:1) 均值未知前提下检验方差是否相等。2) 根据方差检验的结果(方差未知相等、方差未知不等),代入对应的均值检验形式中对均值进行检验。两个正态总体均值及方差的假设检验的理论请参见[2] 。
分布,在方差已知或未知时统计量也有差异。我们的验证步骤为:1) 均值未知前提下检验方差是否相等。2) 根据方差检验的结果(方差未知相等、方差未知不等),代入对应的均值检验形式中对均值进行检验。两个正态总体均值及方差的假设检验的理论请参见[2] 。
在R软件中实现两个正态总体均值及方差的假设检验的函数很多,如R软件的内置程序t.test()可以实现单个、两个正态总体均值的区间估计及假设检验,另一个R软件内置程序var.test()可以实现两个正态总体方差的区间估计及假设检验;文献[2] 中提供的mean.test2()可以实现两个正态总体均值的假设检验和var.test2()可以实现两个正态总体方差的假设检验;文献[4] 中的IntervalEstimate_TestOfHypothesis()可以实现正态总体均值、方差的区间估计及假设检验;文献[5] 中的one_two_sample()可以实现正态总体均值、方差的区间估计及假设检验。为简单起见,本文采用mean.test2()和var.test2()。
在做假设检验时,一般采用P值,若P值小于指定的显著性水平α时,则拒绝原假设;否则不拒绝原假设。
在判断两组专家是否因判断标准不一致而导致评分差异大时,我们简化地只从总分来比较评分均值是否相同。首先进行两个正态总体方差的假设检验,得到的P值见表3。从表3中我们发现,只有样品5的P值小于0.05,可知在表1和表2所给数据基础上,两组专家的评分方差没有较大的差异。
根据表3的方差检验结果,进行两个正态总体均值的假设检验,结果见表4。从表4中我们发现,只有样品2的P值小于0.05,也就是两组专家对样品2的评分均值不等。值得说明的一点是本文在做假设检验时为简化运算将评分求总和,从很大程度上已经减小了评分间的差异程度,从检验结果发现两组专家的评分是基本相符的,由此我们可以认为评比结果有一定的公平性与合理性。
2.3. 多重t检验考察样品区分度[2]
专家评分在实际应用当中主要用于对不同样品的评比,以便对样品的品质进行高低比较,故需要专

Figure 1. The relationships between sample grade and indexes
图1. 样品等级与各项指标之间的关系图
表1. 第一组专家评价总分表
表2. 第二组专家评价总分表
表3. 两个正态总体方差的假设检验P值
表4. 两个正态总体均值的假设检验P值
家组对样品的评分能够反映出样品应有的差异。为了检验专家能否区分样品的品质,我们使用方差分析中均值的多重比较方法。
在方差分析中,我们将样品![]() 作为评分的第
作为评分的第![]() 个水平,两组专家的评分结果
个水平,两组专家的评分结果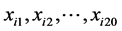 看做来自总体
看做来自总体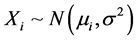 的样本观测值,考虑线性统计模型:
的样本观测值,考虑线性统计模型:
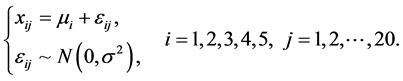
比较不同水平的差异归结为比较这五个总体的均值。多重![]() 检验方法实际上是针对每组数据进行
检验方法实际上是针对每组数据进行![]() 检验,估计方差时利用全体数据,即检验:
检验,估计方差时利用全体数据,即检验:

取检验统计量

当 时,说明
时,说明![]() 与
与 有显著差异。定义相应的P值
有显著差异。定义相应的P值 ,则
,则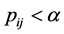 时
时![]() 与
与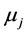 有显著差异。
有显著差异。
多重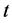 检验使用方便,但由于水平有五个,而检验是同时进行的,多次使用
检验使用方便,但由于水平有五个,而检验是同时进行的,多次使用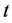 检验法增加了犯第一类错误的概率,故可以对P值进行修正。
检验法增加了犯第一类错误的概率,故可以对P值进行修正。
首先计算各个水平的样本均值,结果见表5。
然后进行均值的多重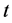 检验,可以不对P值做修正、对P值做holm修正及对P值做bonferroni修正等。这里选取对P值做holm修正,程序及结果如下。
检验,可以不对P值做修正、对P值做holm修正及对P值做bonferroni修正等。这里选取对P值做holm修正,程序及结果如下。
> pairwise.t.test(X, A, p.adjust.method = "holm")
Pairwise comparisons using t tests with pooled SD data: X and A
1 2 3 4
2 2.8e-05 - - -
3 1.7e-05 0.883 - -
4 0.243 0.019 0.015 -
5 0.019 0.243 0.229 0.481 P value adjustment method: holm
从上面的结果可以看出在0.05的显著性水平下,![]() 与
与 、
、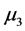 、
、 有显著的差异,
有显著的差异,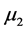 与
与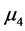 有显著差异,同时
有显著差异,同时 与
与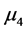 有显著差异。对五个样品的等级从高到低排序得到:
有显著差异。对五个样品的等级从高到低排序得到: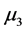 (4级),
(4级),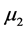 (3.5级),
(3.5级), (3级),
(3级), (2.5级),
(2.5级),![]() (1级)。注意,样品的质量等级已知。由此我们发现,专家们基本上可以区分等级相差为1的样品,但是专家们没有有效地区分出
(1级)。注意,样品的质量等级已知。由此我们发现,专家们基本上可以区分等级相差为1的样品,但是专家们没有有效地区分出![]() 与
与 (等级相差1.5),
(等级相差1.5),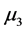 与
与 (等级相差1)。对P值做bonferroni修正下可以得到类似结论。
(等级相差1)。对P值做bonferroni修正下可以得到类似结论。
2.4. 系统聚类[2] [6] [7]
系统聚类类间距离的定义有很多种,本文选取最长距离法、类平均法、重心法及离差平方和法完成
表5. 各个水平的样本均值
系统聚类。我们运用系统聚类的方法将五个样品分为优、良、差三类。做系统聚类时,可以根据两组专家对五个样品评分结果的数据进行系统聚类,结果见图2。也可以根据样品的等级进行系统聚类,得到的图是类似的,故省略。从图中可以得到样品2,3聚为一类,称为优类,样品4,5聚为一类,称为良类,样品1单独为一类,称为差类。
2.5. 判别分析[2] [3] [6]
判别分析是利用已知类别的样本培训模型,为未知样本判类的一种统计方法。判别分析有距离判别分析法、Bayes判别分析法、Fisher判别分析法等。其中距离判别分析法是最简单、最直观的一种判别方法,该方法应用广泛。在应用距离判别分析法进行判别时,待测样本在马氏距离下离哪个总体近,就认为它属于哪一类。相应的判别准则为:

距离判别分析法的R程序及结果如下。
> distinguish.distance(TrnX = data[, 1:10], TrnG = factor(data$A))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 21 22 23 24 25 26 blong 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 | 2 2 2 4 2 2
27 28 29 30 31 32 33 34 35 36 37 38 39 40 | 41 42 43 44 45 46 47 48 49 blong 3 2 2 2 2 2 2 4 2 4 2 3 2 2 | 3 3 3 4 1 3 3 2 2
50 51 52 53 54 55 56 57 58 59 60 | 61 62 63 64 65 66 67 68 69 70 71 72

Figure 2. Hierarchical clustering according to the score results of the five samples by two groups of experts
图2. 根据两组专家对五个样品评分结果的系统聚类
blong 3 3 3 3 3 3 3 3 3 4 4 | 4 4 4 4 4 4 4 4 4 5 4 4
73 74 75 76 77 78 79 80 | 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 blong 4 5 4 4 4 3 4 4 | 5 3 1 5 5 5 5 2 4 5 5 2 5 4 3
96 97 98 99 100 blong 3 1 5 5 5
如果将五个样品各自作为一个类,那么在认为两总体协方差阵不同的情况下,将训练样本回代进行判别,专家的误判数为24个,误判率为24%。从判别结果中我们发现第1类(样品1)只有1个错判,因为第1类(样品1)的等级为1级是最差的,专家们一般不会把它错判为其它的等级;第5类(样品5)有9个错判,因为第5类(样品5)的等级为3级属于居中的等级,专家们可能把它判高也可能把它判低,这也是情理之中的。
现在我们按前面系统聚类分析的结果,把原来的1(样品1),2(样品2),3(样品3),4(样品4),5(样品5)类重新分为1(优),2(良),3(差)类,省略部分程序,距离判别分析法的R程序及结果如下。在认为两总体协方差阵不同的情况下,将训练样本回代进行判别,专家的误判数为20个,误判率为20%,比之前的判别结果有所改进,这也是情理之中的,因为总的类别减少了。从判别结果中我们发现第3类(差)只有2个错判,因为第3类(差)是最差的,专家们一般不会把它错判为其它的等级;第1类(优)有13个错判,专家们大都把它们判为了第2类(良),说明专家们对优的标准很高。
distinguish.distance(TrnX = data3[, 1:10], TrnG = factor(data3$A))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 21 22 23 24 25 26 blong 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 2 3 3 | 1 1 1 2 2 1
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 blong 1 1 1 1 2 1 1 2 1 1 1 2 1 1 1 1 1 2 3 1 2 1 1
50 51 52 53 54 55 56 57 58 59 60 | 61 62 63 64 65 66 67 68 69 70 71 72 blong 1 1 2 1 2 1 1 1 2 2 2 | 2 2 2 2 2 2 2 2 2 2 2 2
73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 blong 2 2 2 2 2 1 2 2 2 2 3 2 2 2 2 1 2 2 2 2 1 2 2
96 97 98 99 100 blong 2 3 2 2 2
总之,若分为5类,则专家们的正确判断率大约为76%,若分为3类,则专家们的正确判断率大约为80%。专家们的判断结果还是很有参考价值的。
现在我们对新样品作判别,R程序及结果如下。
> ## 若分为5类
> distinguish.distance(TrnX = data[, 1:10], TrnG = factor(data$A), TstX = TstX)
1 2 3 4 5 6 7 8 9 10 blong 4 2 3 4 2 3 4 4 4 3
> ## 若分为3类
> distinguish.distance(TrnX = data3[, 1:10], TrnG = factor(data3$A), TstX = TstX)
1 2 3 4 5 6 7 8 9 10 blong 2 1 1 2 1 1 2 2 2 2
从上面的结果中我们发现,若分为5类,则专家们大都把它判为第4类(样品4);若分为3类,则专家们大都把它判为第2类(良)。
3. 结论
本文利用R软件主要讨论了两组专家对葡萄酒样品的评分及专家评分的合理性问题。目前,专家评分对于产品的鉴定或者节目的评选都很严格,它要求专家能够在任何环境下都相对客观地做出评价,并且在积累大量经验后形成一个相对稳定、相对标准的指标,这是难以精准地做到的。故而在实际的专家评分过程中,不同专家对于同样品的评价可能大相径庭,从而影响样品质量的度量。本文从三个方面对两组专家评分进行了讨论分析。
其一,利用两个正态总体均值的假设检验评判两组专家的评分之间是否存在显著差异,从检验结果发现两组专家的评分是基本相符的,由此我们可以认为评比结果有一定的公平性与合理性。
其二,利用均值的多重![]() 检验考察专家们对不同样品的区分度。在0.05的显著性水平下,专家们能够区分样品1与样品2、样品3、样品5,样品2与样品4,样品3与样品4。对五个样品的等级从高到低排序得到:样品3(4级),样品2(3.5级),样品5(3级),样品4(2.5级),样品1(1级)。注意,样品的质量等级已知。由此我们发现,专家们基本上可以区分等级相差为1的样品,但是专家们没有有效地区分出样品1与样品4(等级相差1.5),样品3与样品5(等级相差1)。
检验考察专家们对不同样品的区分度。在0.05的显著性水平下,专家们能够区分样品1与样品2、样品3、样品5,样品2与样品4,样品3与样品4。对五个样品的等级从高到低排序得到:样品3(4级),样品2(3.5级),样品5(3级),样品4(2.5级),样品1(1级)。注意,样品的质量等级已知。由此我们发现,专家们基本上可以区分等级相差为1的样品,但是专家们没有有效地区分出样品1与样品4(等级相差1.5),样品3与样品5(等级相差1)。
其三,运用系统聚类的方法将五个样品分为优、良、差三类,然后采用距离判别分析法,利用训练样本建立判别函数,将训练样本回代进行判别,得到专家的误判率和正确率,最后利用判别函数对新的样本进行判类。
基金项目
重庆市自然科学基金项目(CSTC2011BB0058)。
参考文献 (References)
- [1] R Core Team (2014) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org/
- [2] 薛毅, 陈丽萍 (2007) 统计建模与R软件. 清华大学出版社, 北京.
- [3] 杨虎, 刘琼荪, 钟波 (2004) 数理统计. 高等教育出版社, 北京.
- [4] 张应应, 魏毅 (2014) R函数实现正态总体均值、方差的区间估计及假设检验的设计. 统计与决策, 9, 74-77.
- [5] Zhang, Y.Y. (2013) OneTwoSamples: Deal with one and two (normal) samples. R package version 1.0-3.
http://CRAN.R-project.org/package=OneTwoSamples - [6] 王学民 (2009) 应用多元分析. 第3版, 上海财经大学出版社, 上海.
- [7] 方开泰 (1982) 有序样品的一些聚类方法. 应用数学学报, 1, 94-101.
