Statistics and Application
Vol.
08
No.
01
(
2019
), Article ID:
28351
,
12
pages
10.12677/SA.2019.81002
Measurement and Empirical Analysis of Listed Companies Debt Default Probability via KMV Model
Kaihao Liang*, A’yun Niu
College of Computational Science, Zhongkai University of Agriculture and Engineering, Guangzhou Guangdong

Received: Dec. 16th, 2018; accepted: Dec. 31st, 2018; published: Jan. 7th, 2019

ABSTRACT
How to measure the default risk of debt of listed companies has always been a hot topic in risk management. In this paper, KMV model is used to analyze relevant data of financial statements issued by listed companies in China, and the probability of their debt default is studied. The default probability of debt of listed companies based on KMV model is established, and the default probability of 41 listed companies in China’s securities market in 2012 is measured by the model. Meanwhile, 41 listed companies were divided into industries for similar analysis and inter-class analysis. The empirical results show that when the company’s asset-liability ratio is higher than 80%, regardless of its net asset liability ratio, it has a high credit risk, while when the company’s asset-liability ratio is lower than 50%, as long as there is no negative return on equity, the company is less likely to default.
Keywords:KVM Model, Default Probability, Listed Company, The Credit Risk
基于KMV模型的上市公司债务违约概率度量与实证分析
梁凯豪*,牛阿云
仲恺农业工程学院计算科学学院,广东 广州

收稿日期:2018年12月16日;录用日期:2018年12月31日;发布日期:2019年1月7日

摘 要
如何准确度量上市公司债务的违约风险一直是企业债务风险管理的研究热点。本文运用KMV模型,通过分析我国上市公司发布的财务报表,就它们的债务违约概率问题进行了相关研究。本文建立了基于KMV模型的上市公司债务违约概率,应用模型实际度量了2012年我国证券市场上41家上市公司的违约概率。同时,将41家上市公司分行业进行同类分析以及类间分析。实证结果表明,当企业的资产负债比大于80%时,无论其净资产负债比率高低,均具有较高的信用风险,而当企业的资产负债比率低于50%,那么只要没有出现负净资产收益率,则公司违约的可能性较低。
关键词 :KVM模型,违约概率,上市公司,信用风险

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 研究背景和意义
上市公司的债务违约给投资者带来巨大损失,是金融监管部门所面临的一个重大课题。如何准确度量上市公司债务的违约概率,降低其违约风险是风险管理者需要解决的一个主要问题 [1] [2] 。
信用风险的计量大致经历了专家判断法 [3] 、信用评分模型 [4] 、现代信用风险违约概率 [5] 三个发展阶段。20世纪90年代,由Credit Monitor模型发展而来的KMV模型由于其基于Merton的期权定价理论,直接使用企业的股票市场数据而会计信息和历史数据的依赖性低,具有较高的准确性和理论基础强等优点 [6] [7] ,被世界众多银行和公司所使用。从中国市场发展的特点来看,KMV模型是更为适合的度量中国上市公司信用风险的模型。
本文的贡献在于利用KMV模型,将银行的贷款问题倒转过来,从借款企业的股权所有者的角度来看待借款偿还的激励问题,建立了上市公司资产市价和股票波动率估计的数学模型,然后分别对银行、旅游、石油以及地产四个行业的部分股票进行违约概率实证分析,得到相关的结论。
2. KMV模型建立
根据Merton的理论,债务合同被视为一种期权合约,借款人的违约概率取决于其资产市值的变化 [8] 。对债权人而言,投放贷款就意味着卖出了一份贷款违约的看跌期权:当借款人资产的价值小于债务时,借款人就会选择违约。这样,借款人的损失仅限于股本损失。而对于债权人来说,其损失为借款人剩余资产和债务的差额,差额越大,损失越大。反之,当借款人的资产价值大于债务时,借款人会选择履行债务合同,即不违约 [9] [10] [11] 。这样,借款人的损失仅限于利息,而债权人的收益仅限于利息。
KMV公司的KMV模型认为,当企业的资产低于全部债务价值的某个临界平时,企业一般会选择违约,并将这一临界点成为违约点(DPT)。它等于企业短期债务(STD)和一半长期债务(LTD)之和 [12] :
(1)
以下为了计算方便,令企业资产在期初时为V0,在期末T的资产为Vt,违约点处的债务为DPTt。则企业的违约概率为:
(2)
同时,根据Black-Scholes期权定价模型,风险资产价值的变化被认为服从几何布朗运动过程,即:
(3)
其中, 为常数漂移项,代表资产回报均值, 为常数资产的回报波动率,z代表一个维纳过程。假设对于所有时间T,该风险资产的价值分布成对数正态分布,即:
(4)
将式(4)代入式(2),假定投资者是风险中性的,即将 换成r,则:
(5)
KMV将 定义为违约距离(DD),即资产价值最终分布的均值与违约临界值之间的距离是资产未来汇报变准成的倍数。
由此计算出来的违约概率是“风险中性”的,即投资者预期回报水平等于无风险利率时的违约概率而不是基于预期回报的“实际”违约概率 [13] 。
3. 参数估计
根据期权理论,影响上市公司违约概率有4大变量:即资产的市场价格 、违约点 、股票价格在时间t内的估计波动率 、无风险利率r。
3.1. 公司资产市场价值的设定
公司资产的市场价值包括了公司股权的市场价值和所有债务的市场价值 [14] ,而股权的市场价值可通过账面价值,债务的市场价值则表现为股权市值。于是,公司资产市价 就等于公司的账面价值D加上股权市值 ,即:
(6)
根据期权理论的假设条件,上市公司资产必须具有完全流动性,所有资产的价格遵循连续的随机过程 [15] 。而中国的实际情况是,国有股和法人股在股票市场不流通,因此,这里我们假设我国上市公司在财务报表中所呈现的资产总值具有完全流通性,以其资产总值作为上市公司资产的市场价值 的估计值。
3.2. 违约点
通过对上市公司违约的大量案例,我们可以知道,当公司资产价值不低于公司总负债账面价值时,公司一般不选择违约;公司出现违约最频繁的临界点处是在流动负债加上长期负债的一半,这正是KMV公司选取的违约点。我们这里也是选取同样的违约点。
3.3. 上市公司资产市场价值的波动率
这里利用上市公司股票价格的历史数据估计其年波动率。给出以下定义:n表示观察到的样本个数, 表示在第t个时间间隔末的上市公司股票价格,时间间隔的长度 (以年为单位),再令
,其中, (7)
由于 ,故 就是第i个时间间隔后的连续复利收益(并非以年为单位)。的标准差通常估计为
或 (8)
其中“ ”为 的均值。
由于 的标准差为 ,而变量s是 的估计值,所以 本身可以被估计为 ,其中 。
3.4. 无风险利率
由于无风险利率是一种理想状态利率,因此,这里用中国人民银行公布的一年期贷款利率来估计无风险利率。
4. 实证分析
4.1. 样本选取
本文选择中国上海证券交易所和深圳证券交易所上市的A股股票(剔除有发行B股或者H股的股票,只考察发行A股的上市公司),选择了41只股票,如表1,按其所属不同的行业类型分为四类:银行类、旅游类、石油类以及地产类。为了避免公司规模对实证结果的影响,选择的研究公司主要依据总资产规模相近这个条件选取。数据来源于国信金太阳独立交易软件。
本文选取的所有样本公司均已完成股改,时间范围是从
Table 1. Industry distribution of sample companies
表1. 样本公司的行业分布
4.2. 违约距离和违约概率的计算
通过计算,可得到如表2所示的各上市公司资产市场价值以及股票价格波动率估计值的数据结果:
Table 2. Assets market value and volatility of sample companies
表2. 样本资产市值和波动率
由于上市公司债务在一年内无较大变化,因此,直接采用2012年第一季以及第三季违约临界点的平均值作为整年的临界点DPT,如表3所示。
Table 3. Critical point of sample companies
表3. 样本临界点
根据式(
Table 4. Default distance and default probability
表4. 违约距离和违约概率
4.3. 同类对比
(一) 建材类

Figure 1. Building materials category
图1. 建材类
由图1所示的两轴线–柱图,可以明显的看到,建材类公司的违约概率大致在0.05~0.30之间,而所选的样本公司中,洛阳玻璃的违约概率是最大的,达到了0.28449,而旗滨集团的违约概率是最小的,为0.00663,它们的违约距离相差了0.27786,由此可见,洛阳玻璃较旗滨集团更容易违约。
由于本文计算上市公司违约概率时,主要依赖的是公司财务报表的数据,由上市公司的资产与债务状况来判断公司的信用风险,如表5。在分别对公司财务状况进行分析时,发现洛阳玻璃的资产负债比率明显高于淇滨集团的资产负债比率,并且,洛阳玻璃的净资产收益率也显著低于旗滨集团的净资产收益率,由图1所示。因此,可以说,建材的违约概率与它们的资产负债比率存在一定的负相关关系,与它们净资产收益率存在一定的正相关关系,若建材类公司想提高自己的信用风险,则需尽量减少负债,提高自身的净资产收益率。
Table 5. Financial status of building materials companies
表5. 建材类公司的财务状况
(二) 石油类
从图2中,可以明显的看到,石油类的违约概率主要在0.00~0.17之间,并且出现了严重的两级分化,一部分石油公司出现了很低的违约概率甚至是不违约,其中表现为不违约的上市上司公司有广聚能源、泰山石油、茂化实业以及岳阳兴长,而另一部分石油公司的违约概率则在0.14~0.17之间,其中包括龙宇燃油(0.16990)以及天利高新(0.14883)。
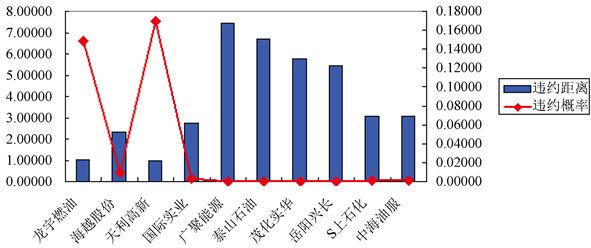
Figure 2. Category of petroleum
图2. 石油类
分别从财务数据中来分析表现出两种极端的公司的情况,从表6中,可以看到违约概率表现为零的上市公司的资产负债率都小于15%,由此可以看出,这些公司的负债占了公司资产较小的一部分。违约表现在当公司资产的市场价值小于债务临界值时,而违约的临界值又取决与公司债务的大小。尽管资产负债率小的上市公司的净资产收益率很小,但由于它们负债较少,因此,从目前的历史数据来看,还不至于表现为违约。而违约概率不为零的两家上司公司,它们的负债都超过公司资产的一半,并且,净资产收益率不高甚至还出现了负收益,它们的违约风险明显就高于资产负债率小的公司。
Table 6. Financial status of oil companies
表6. 石油类公司的财务情况
(三) 旅游类
由图3所示的旅游类违约距离及违约概率,可以发现,样本上市公司的违约概率在0.00~0.01之间,可见,旅游类上市公司的信用风险相对较高,很少公司会出现违约的情况。而由计算结果发现的部分公司出现不违约的情况,同样的也能从公司的财务报表的相关数据中得以解释,如表7所示。
旅游类上市公司的资产负债比率都在50%以下,这些公司的负债都小于资产的负债,证明公司能够及时偿债以不至于达到违约的境地。违约概率呈现为零的上市公司的资产负债比率都在40%以下,尽管有的净资产收益率很低,但由于负债的比率很小,使公司能够维持很好的经营,以不至于违约,如北京旅游,虽然它的净资产收益率仅有1.63%,远远小于同类的平均净资产收益率,但也因为它的资产负债比率也远远小于其他公司的资产负债率,为12.37%,因此,就算公司的经营情况不佳,负债较小也能保持较小的信用风险。

Figure 3. Tourism category
图3. 旅游类
Table 7. Financial status of tourism companies
表7. 旅游类公司的财务情况
(四) 房地产类

Figure 4. Real estate category
图4. 房地产类
房地产类的上市公司违约概率一般在0.00~0.40之间,从图4中可以看到,大于一半的公司拥有较好的信用,它们的违约概率都比较低,大致都在0.00~0.01之间,如宜华地产(0.00664),而有些公司却存在较高的信用风险,如中茵股份(0.35358)、天业股份(0.22101)、沙河股份(0.22896)等。
由表8所示的违约概率较低与违约概率较高的两种房地产公司的财务报表对比,可以看到,违约概率较低的宜华地产尽管它的净资产收益率较低,负债也占了资产的一半多,但相比于负收益的沙河股份,它依旧能保持较好信用。尽管违约概率较高的上市公司拥有较高的净资产收益率,如天业股份、中茵股份,但是它们负债占了资产很大的比重,因此,它们比较容易造成资不抵债,形成较高的信用风险。
Table 8. Financial status of real estate companies
表8. 房地产类公司的财务情况
(五) 同类对比小结
利用各个上市公司不同的财务状况以及分行业进行如上所述的同类对比,可以发现,上市公司的信用风险与它们本身的内部发展存在莫大的关系。尽管各个行业都具有不同的特点,但是,如果一个上市公司的资产负债比率较大,达到了80%或以上,无论它的收益有多好,依旧会有很高的违约概率,相反的,假如它的资产负债比率较小,在50%左右甚至以下,在不出现负收益的情况下,它还是能保持较好的信用。
4.4. 类间对比
如上所述,不同的行业存在不同的特点,那不同行业之间的债务的违约概率是否又会存在一定的共性呢?这就要依赖于以下的研究。通过对KMV模型的了解,我们知道违约概率是服从于标准正态分布特点的,因此,利用SPSS软件对不同行业上市公司债务的违约概率进行两两对比,得出以下结果,如表9所示。
通过将四个行业的违约概率分别进行对比检验,得出如上六种对比结果:房地产类是四个行业里面风险最高的,它的违约概率达到了0.1166,风险最低的旅游类高出0.1146。在计算违约概率的时候,主要依赖的是上市公司的资产与负债,而从公司的财务报表中,房地产类公司的资产负债比率明显高于旅游类公司的资产负债比率,而旅游类公司的总体净资产收益比率高于房地产公司的资产负债比率,因此,正如前面所述,上市公司的为违约概率与其资产负债比率成一定的正相关关系,而与其净资产收益比率成一定的负相关关系,正如T检验显示,建材类与旅游类得出的统计值为3.016,在假设两者不存在差异性的情况下得出这样的结果,证明两类之间存在很大的差异性。石油类与旅游类是差异最小的两个行业,它们的违约概率仅相差0.0314,而T统计量的值为1.49,明显证明了它们两个行业在信用风险方面雷同。从分别对石油类及旅游类进行违约概率的分析结果中,可以看到两个行业均存在违约概率为零的情况,而这些情况都是由于上司公司的净资产收益率较低或资产负债比率较小所导致的,因此,以来上市公司的财务状况对违约概率的研究发现石油类与旅游类两个行业的上市公司在信用风险上存在相似性。
Table 9. Comparison results between categories
表9. 类间对比结果
5. 结论
通过以上的实证研究以及对比分析,本文得出在依赖于上市公司的资产负债情况对它们进行违约概率研究的情形下,当公司的资产负债比率较高,达到80%左右时,则存在较高的信用风险,而当公司的资产负债比率较低时,只要它不存在负净资产收益比率,则一般都不会导致违约,具有较好的信用。
在利用KMV模型对上市公司债务的违约概率研究中,也发现了如下几个问题:
第一:关于违约点的选择。本文的违约点选取的是公司财务报表所呈现的流动负债与一半长期负债之和,在公司的资产负债比率较小(低于15%)的情况下,计算出来的违约概率为零,这并不能完全说明该公司不存在违约的状况,只是它的信用风险比其他公司的信用风险低而已,而真正的违约情况并不能由此判别出来。因此,要更好的研究公司的违约概率,违约点的选择是一个关键问题 [16] 。
第二:金融市场数据的透明度不够。由上述分析过程,可以看到KMV模型的大量数据来源于上市公司财务报表和资本市场,样本数据的可靠性至关重要,直接影响信用风险的大小。上市公司应及时进行信息公开,这样模型才能真实地反映上市公司的信用状况 [17] 。
第三:KMV模型的理论数据与经验数据之间仍存在较大的差距,因此,应通过积累大量数据并反复验证才能使得模型参数更好的得出真实结果。
致谢
本研究受广东省自然科学基金(编号:2018A0303130136)、广东省科技计划项目(编号:2015A070704059)、广东省省级乡村振兴战略专项资金项目(编号:粤财农[2018]125号)、广东省教育厅育苗工程项目(编号:2012WYM_0081)资助完成,在此对资助者一并致谢。
文章引用
梁凯豪,牛阿云. 基于KMV模型的上市公司债务违约概率度量与实证分析
Measurement and Empirical Analysis of Listed Companies Debt Default Probability via KMV Model[J]. 统计学与应用, 2019, 08(01): 6-17. https://doi.org/10.12677/SA.2019.81002
参考文献
- 1. 都红雯, 杨威. 我国对KMV模型实证研究中存在的若干问题及对策思考[J]. 国际金融研究, 2004(11): 22-27.
- 2. 程鹏, 吴冲锋. 上市公司信用状况分析新方法[J]. 系统工程理论方法应用, 2002(2): 89-93.
- 3. 郑茂. 基于EDF模型的上市公司信用风险实证研究[J]. 管理工程学报, 2005(3): 151-154.
- 4. 梁世栋, 李勇, 方兆本. 信用风险模型比较分析[J]. 中国管理科学, 2002(2): 35-43.
- 5. 程鹏, 吴冲锋, 李为冰. 信用风险度量和管理方法研究[J]. 管理工程学报, 2002(1): 77-73.
- 6. Chang, C. (2012) Default Probability of a Captive Credit Bank with Government Capital Injections: A Capped Barrier Option Approach. Economic Modelling, 29, 2444-2450. https://doi.org/10.1016/j.econmod.2012.07.009
- 7. Perko, I. (2017) Behaviour-Based Short-Term Invoice Probability of Default Evaluation. European Journal of Operational Research, 257, 1045-1054. https://doi.org/10.1016/j.ejor.2016.08.039
- 8. Denzler, S.M., et al. (2006) From Default Probabilities to Credit Spreads: Credit Risk Models Do Explain Market Prices. Finance Research Letters, 3, 79-95. https://doi.org/10.1016/j.frl.2006.01.004
- 9. Hainaut, D. and Deelstra, G. (2014) Default Probabilities of a Holding Company, with Complete and Partial Information. Journal of Computational and Applied Mathematics, 271, 380-400. https://doi.org/10.1016/j.cam.2014.04.003
- 10. Melgarejo, M. (2018) Beating Market Expectations and the Pricing of Firms’ Probability of Default. Journal of Contemporary Accounting & Economics, 14, 41-51. https://doi.org/10.1016/j.jcae.2018.02.005
- 11. Tabak, B.M., Luduvice, A.V.D. and Cajueiro, D.O. (2011) Mod-eling Default Probabilities: The Case of Brazil. Journal of International Financial Markets, Institutions and Money, 21, 513-534. https://doi.org/10.1016/j.intfin.2011.01.007
- 12. Cantia, C. and Tunaru, R. (2017) A Factor Model for Joint Default Probabilities. Pricing of CDS, Index Swaps and index Tranches. Insurance: Mathematics and Economics, 72, 21-35. https://doi.org/10.1016/j.insmatheco.2016.10.004
- 13. Hao, X., Li, X. and Shimizu, Y. (2013) Finite-Time Survival Probability and Credit Default Swaps Pricing under Geometric Lévy Markets. Insurance: Mathematics and Economics, 53, 14-23. https://doi.org/10.1016/j.insmatheco.2013.04.003
- 14. Câmara, A., Popova, I. and Simkins, B. (2012) A Com-parative Study of the Probability of Default for Global Financial Firms. Journal of Banking & Finance, 36, 717-732. https://doi.org/10.1016/j.jbankfin.2011.02.019
- 15. Trussel, J. (1997) Default Probability on Corporate Bonds: A Contingent Claims Model. Review of Financial Economics, 6, 199-209. https://doi.org/10.1016/S1058-3300(97)90006-9
- 16. Grammenos, C.T., Nomikos, N.K. and Papapostolou, N.C. (2008) Estimating the Probability of Default for Shipping High Yield bond Issues. Transportation Research Part E: Logistics and Transportation Review, 44, 1123-1138. https://doi.org/10.1016/j.tre.2007.10.005
- 17. 梁琪. 我国商业银行信贷风险管理体系构建探索[J]. 南开经济研究, 2002(6): 14-16.
NOTES
*通讯作者。
