Advances in Condensed Matter Physics
Vol.04 No.04(2015), Article ID:16340,9
pages
10.12677/CMP.2015.44014
Charge-Transfer Metal-Insulator Transitions and Electronic Properties in Vanadium Dioxide
Longjuan Kong1, Guanghua Liu1*, Ling Qiang2
1Department of Physics, Tianjin Polytechnic University, Tianjin
2School of Physics, Peking University, Beijing
Email: *liuguanghua@tjpu.edu.cn
Received: Oct. 27th, 2015; accepted: Nov. 10th, 2015; published: Nov. 13th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In the framework of density functional theory, the electronic structure and the metal-insulator transition (MIT) mechanism of vanadium dioxide are investigated by GGA + U method. With on- site correlation effects, insulating states can be obtained in both high temperature rutile and low temperature monoclinic structures. Suddenly opening of the energy gap in the monoclinic phase is consistent with the experimental observation. Furthermore, an interesting charge-transfer from the center V ion to the 6 O ligands has been found during the MIT process, which suggests that such a MIT should be a charge-transfer type.
Keywords:Metal-Insulator Transition, Electronic Property, Charge-Transfer

二氧化钒电荷转移型金属绝缘体相变 及电学性质研究
孔龙娟1,刘光华1*,强凌2
1天津工业大学物理系,天津
2北京大学物理学院,北京
Email: *liuguanghua@tjpu.edu.cn
收稿日期:2015年10月27日;录用日期:2015年11月10日;发布日期:2015年11月13日

摘 要
在密度泛函理论框架下,利用GGA + U方法,本文对二氧化钒的金属绝缘体相变及电学性质进行了详细的研究。研究发现,一旦考虑占位关联效应,不管在高温R相还是低温M1相的二氧化钒中都可以得到绝缘体态。然而在M1相中,能隙的突然打开现象与实验观测现象非常一致。另外,在金属绝缘体相变过程中,中心钒原子和其周边的6个氧配位体之间发生了一个有趣的电荷转移现象。这一现象表明二氧化钒中发生的金属绝缘体相变应该属于电荷转移型。
关键词 :金属绝缘体相变,电学性质,电荷转移

1. 引言
过渡金属氧化物作为强关联电子模型体系,蕴含着丰富的结构和新奇的物理现象。如温度导致的金属绝缘体相变,伴随着光、电、磁等物理性质的突变,在激光致盲、红外遥感、太阳能温控乃至锂离子电池等诸多领域具有重要的应用前景,一直是凝聚态物理、材料领域极为关注的重要对象。很多过渡金属氧化物都有这种相变特性,如Ti2O3,Fe3O4,Mo9O26,VnO2n-1等[1] [2] ,其中以相变温度接近室温的二氧化钒(VO2)最引人注目。因为室温范围内的温度控制比较容易,而且室温范围内的相变最有可能应用到实际中,所以在众多的过渡金属氧化物中,VO2常常受到更大的关注[3] -[19] 。研究发现VO2相变温度在340 K (68℃)左右,接近室温,就是说VO2在340 K左右时会发生从金属相到绝缘体相的可逆突变[20] 。在高于转变温度时,VO2为金红石四方相结构(R),空间点群为P42/mnm,呈金属性。然而当温度低于转变温度时,VO2的稳定相为单斜晶相结构(M1),空间点群为P21/c,呈绝缘体(半导体)性,其带隙~0.6 eV。如图1所示,在VO2(R)结构中,V原子占据在单位晶胞的8个顶角和中心位置,且和周围6个O原子形成VO6八面体单元。当发生VO2(R)到VO2(M1)的相变时,V原子发生移动,偏离原来晶胞顶点位置且沿着c轴方向两两形成距离更近的倾斜V-V键(此称为V-V二聚化),因此在c轴方向形成长和短的折线形V-V链(zigzag链)。VO6八面体结构也从较正的八面体变为扭曲的八面体。因此随着温度的降低,VO2会发生从金属性质到非金属(或绝缘体)性质的相变(Metal-Insulator Transition (MIT)),同时还伴随着晶体向对称程度较低的结构相变(structural phase transition (SPT))。
VO2相变物理机制的研究一直是人们非常感兴趣的问题,一方面是因为它的广泛的应用前景,另一方面是VO2作为过渡金属氧化物的代表,对其深入的理论研究可以帮助人们了解过渡金属氧化物特殊的相变性质。对于VO2相变物理机制目前主要有两种代表性的观点:结构驱动的Peierls转变以及电子关联驱动的Mott-Hubbard转变。Peierls机制认为相变晶体超过临界温度点时,晶体晶格将发生畸变,最终导致晶体的性质从金属态转变为绝缘体态[21] 。Mott-Hubbard机制认为一级MIT是由电子的强关联作用导致的[22] [23] 。VO2的相变机制过程很复杂,到目前为止科学界对VO2相变的解释还没有形成一个统一的认识。Goodenough [11] ,最早运用分子轨道理论研究了VO2的电子结构,并认为晶格结构的扭曲是MIT的起源,因此支持Peierls转变机制。之后,Wentzcovitch等人[15] 的局域密度近似计算结果证实了

Figure 1. Geometric schematic pictures of VO2 with rutile and monoclinic symmetries
图1. 金红石相与单斜相VO2结构示意图
Goodenough的观点,通过能带理论分析了结构扭曲导致VO2能带结构变化,发现绝缘相的能隙形成来源于近邻V-V键(主要是V的d-d轨道交叠)的加强,也就是说VO2应该是能带型(或Peierls型)绝缘体而不是关联型(或Mott-Hubbard型)绝缘体。遗憾的是他们并没有得到VO2的单斜绝缘体晶相结构,也没有给出准确的VO2带隙。除此之外,Peierls不能解释相变过程中出现的亚稳相(M2),也称为中间绝缘体相。VO2 M2的结构与VO2 M1十分相似,只是在c轴方向上一半的V原子继续呈现二聚状态,而另一半的V原子则形成等距离的zigzag型长链。于是,1975年Zymersztejn和Mott [13] 提出Mott相变的观点,认为电子关联能(Hubbard U)是导致MIT和SPT的主要原因,特别是d轨道的强电子关联作用是产生绝缘相光学带隙的主要原因。Laad等人[24] 利用局域密度近似(Local Density Approximation, LDA)加上动力学平均场理论(Dynamical Mean Field Theory, DMFT)研究了VO2中的关联效应,他们的研究发现载流子浓度的增加是金属绝缘体相变的主要原因。利用基于第一性原理的全势线性muffin-tin轨道组合(FP-LMTO)方法,Huang等人[17] 给出了Peierls和Mott-Hubbard机制对于VO2具有同等重要性的结论。
以上提到的人们对于VO2相变机制的争议主要是由于MIT和SPT在相变过程中同时发生导致的。然而近年来,实验技术和探测手段的逐步升级,使得一些科研工作者在观察金属绝缘体的相变过程中成功分离了晶格结构转变与电学性质转变。Kim等人[7] -[9] 用外加直流电场的方式诱导VO2发生金属绝缘体相变,同时结合Raman光谱或者X射线表征结构,结果显示在金属化发生时VO2并没有发生结构相变,MIT先于SPT发生,而且在MIT和SPT之间出现了单斜的关联金属相,即当VO2己转变为金属态时仍然保持单斜结构。之后发生的结构相变是由于金属化产生的热效应导致。这说明了VO2的MIT属于Mott转变类型。此外,2007年,Arcangeletti等人[25] 对VO2 (M1)体材料进行了最高压力分别为19 GPa和14 GPa的拉曼测试与红外测试,指出样品的晶体结构与带隙在10 GPa前并没有明显变化,而10 GPa后样品发生了压致金属化,同时认定该金属化相变仍然发生在单斜结构中。以上研究工作有力的说明了在没有发生SPT的情况下,也可以实现VO2的金属绝缘体相变。
虽然对于VO2 MIT机制已经有了一些理论研究结果,但是究竟是哪种机制起作用,到目前为止还没有达成一致意见,还需要人们做进一步研究。因此本文将采用基于密度泛函理论(Density Functional Theory, DFT)的第一性原理计算方法对VO2的电学性质进行系统的计算和分析,包括能带结构、布居分布以及能态密度等。然后,从原子层面上对VO2金属绝缘体相变机制做进一步更深入的研究。
2. 计算方法与模型
本文采用基于DFT的第一性原理计算方法,利用Materials Studio软件中CASTEP模块[26] 计算VO2的总能量和电学性质。该模块利用平面波赝势方法将离子势用赝势替代,电子波函数用平面波基矢组展开。电子与电子相互作用的交换关联能采用广义梯度近似(Generalized Gradient Approximation, GGA) [27] 下改进的函数(Revised Perdew-Burke-Eruzerhof, RPBE) [28] 来描述。在晶体周期性势场中,采用三维周期性边界条件将多电子体系用平面波函数展开表示。为尽量减少平面波基个数,采用超软赝势来描述离子实与价电子之间的相互作用。系统总能量和电荷密度在Brillouin区的积分计算使用Monkhorst-Pack [29] 方案,选择k网格点为:5 × 6 × 6,以保证体系能量和构型在准完备平面波基水平上的收敛。为了确保计算速度并能满足足够的精度,在计算时平面波截止能量取340 eV。由于V原子存在电子的d轨道的强关联效应,我们采用GGA结合Hubbard U模型(GGA + U)对强的局域态电子(V 3d)进行修正。其中U (Hubbard )是位库伦势描述了V 3d轨道电子间的局域库仑相互作用效应。
本文计算使用了两种结构的晶胞作为计算模型。高温相VO2为金红石结构,空间群为P42/mnm (136),对称行为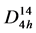 ,晶格常数为a = b = 4.555 Å,c = 2.851 Å,晶格原胞包含一个V原子和一个O原子,原子坐标为V (0, 0, 0),O (0.3, 0.3, 0) [30] 。低温相VO2为单斜结构,空间群为P21/c (14),对称性为
,晶格常数为a = b = 4.555 Å,c = 2.851 Å,晶格原胞包含一个V原子和一个O原子,原子坐标为V (0, 0, 0),O (0.3, 0.3, 0) [30] 。低温相VO2为单斜结构,空间群为P21/c (14),对称性为 ,晶格常数为a = 5.752 Å,b = 4.538 Å,c = 5.383 Å,晶格原胞包含一个V原子和两个O原子,原子坐标为V (0.239, 0.979, 0.026),O1 (0.106, 0.212, 0.209),O2(0.401, 0.703, 0.299) [31] 。两种结构的示意图如图1所示。
,晶格常数为a = 5.752 Å,b = 4.538 Å,c = 5.383 Å,晶格原胞包含一个V原子和两个O原子,原子坐标为V (0.239, 0.979, 0.026),O1 (0.106, 0.212, 0.209),O2(0.401, 0.703, 0.299) [31] 。两种结构的示意图如图1所示。
3. 计算结果与讨论
原子轨道线性组合方法为我们计算和分析原子电荷分布、重叠布居以及原子间的电荷转移提供了有力的理论依据。首先,计算了中心V离子与6个氧配位体之间的重叠布居(也称为键布居)。可以用计算得到的沿键方向的重叠布居来判断V-O之间价键的离子性或共价性的强弱以及它们之间共享电子的程度。通过对V与O之间重叠布居数的计算和分析,我们发现布居数与两原子之间的距离相关联,即重叠布居值越大,则两原子之间共价性越强,原子之间的距离越短。但是重叠布居数并不受占位库仑相互作用(U)的影响。对于不同的值,R相VO2的重叠布居数有两个固定的值0.25和0.7,分别对应两种不同的键长1.9323和1.9215。R相VO2的平均重叠布居为0.556,但是对于M1的平均重叠布居数为0.36,则两者的比值为1.5,说明R相中V-O的共价性比M1相中V-O的共价性强。
然后,我们分别计算了两种相结构的能带,图2分别给出了带隙(Eg)随着U的变化曲线。从图2中可以看出,对于R相结构VO2的占位库仑相互作用U~5.3时带隙值大于0 eV,呈现出绝缘体特性;而对于M1相结构而言,当U~4.78时带隙突然打开,表现为绝缘体特性。这种现象说明MIT发生时,VO2并没有发生SPT。然而两种相结构由金属到绝缘体的转变有着完全不同的特点。在M1相中,当U达到4.78 eV时,带隙值从0 eV突变到0.32 eV。此时的能带结构图如图3所示。从图中可知,带隙(Eg~0.32 eV)价带顶和导带底在动量空间中不同对称点的间接带隙,而在同一对称点D处的直接带隙值为0.58 eV。此时的间接带隙值(0.32 eV)可以用来解释Verleur等人[32] 在试验中测到的在0.31 eV处突然发生光传输的现象。但是间接带隙在实验中并不容易观测到,这是因为对于间接带隙的绝缘体,单纯的光吸收并不能使电子由价带顶跃迁到导带底,必须在吸收光子的同时伴随着吸收或发射一个声子以遵守跃迁定则中的动量守恒定律。与直接带隙中电子跃迁相比,间接带隙中的跃迁是个二级过程,发生的几率要小得多,因此试验中观测到的光学带隙通常为直接带隙。所以本计算中所得到的直接带隙(~0.58 eV)与Ladd and Paul [33] 在试验中测得光学带隙(0.6 eV)吻合的很好。进一步分析图2,我们还可以发现当Hubbard U值为4.78时R相结构的VO2带隙为0 eV表现为金属特性,而M1相结构具有~ 0.32 eV的带隙呈绝缘体特性。然而Koethe等人[34] 利用LDA + U的方法得出了R相和M1相均为绝缘体的结论。与文献[34] 相比我们的结果更符合实验现象。因此,我们认
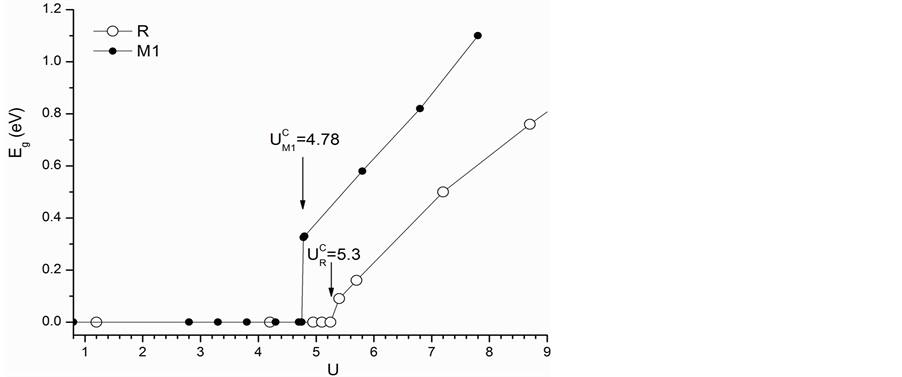
Figure 2. Energy gap (Eg) of M1 and R phases versus varying U
图2. M1相和R相VO2的能隙(Eg)随U值的变化曲线

Figure 3. Energy band structure of insulating monoclinic VO2 with U = 4.78
图3. 当占位库仑相互作用U = 4.78时单斜相VO2的能带结构图
为VO2中V的占位库伦相互作用势为4.78。
为了定性的考察M1相结构中电子占据数随着U的变化,本文对VO2中的V离子进行了Mulliken原子布居分析,结果如图4所示。其中图4(a)给出了V离子的原子布居数随着U值得变化曲线。由图4(a)中容易发现,当在不考虑库仑相互作用势能时V离子的原子布居数为正值,说明V离子带正电荷。V离子的原子布居数随着U值得增加而增加,但是当U值增大到4.78时,突然出现了一个明显的峰。这一现象说明,在MIT过程中大量的电子从中心V离子转移到了6个O配位体。因此我们可以得出这样的结论:在不引起其它效应(例如结构扭曲或声子散射)的情况下,电子之间的库仑相互作用力可以引起MIT。同时,中心钒原子和其周边的6个氧配位体之间发生的一个有趣的电荷转移现象表明二氧化钒中发生的金属绝缘体相变应该属于电荷转移型[35] -[38] 。伴随着原子布居数的突然增加,不同二聚体相邻V离子之间的重叠布居数会突然减小,出现一个向下的峰值(如图4(b)所示)。根据Mulliken原理我们知道当布居数为负值时表示两原子之间成反键(库仑排斥作用)。因此我们的计算结果表明在U = 4.78相变点,不同二聚体相邻V离子之间出现了明显的排斥作用力导致之间的距离变长,而与此同时沿c轴方向的同一二聚体中V-V之间距离会缩短,结构更加的稳定。为进一步探索MIT机制,我们计算了M1相结构VO2中3d轨道的分波态电子态密度(PDOS)。U取不同值时V-3d轨道的PDOS如图5所示。通过分析图5可知,随着U值的逐渐增加,PDOS曲线整体向高能方向漂移。此外更为明显的现象是随着U值的增加,费米能级附近的PDOS峰值不断降低,与之相对应的是O-2p轨道的电荷数的增加。这种现象是由前面所讨论的电荷转移导致的。
最后,为了研究M1相结构VO2的磁学特性,我们计算了自旋向上和自旋向下的态密度分布(如图6)。由图6可得,电子自旋向上和自旋向下的态密度分布存在着差别,并不能完全重合,因此具有绝缘体性质的M1相VO2呈现出铁磁性而不是反铁磁性。因为Mott型绝缘体通常表现出反铁磁性,例如V2O3 MIT就是典型的Mott-Hubbard型,它的自旋向上和自旋向下的态密度分布完全重合(如图7所示)具有反铁磁性,所以比

Figure 4. The V atomic populations (a) and the V-V bond (overlap) populations (b) with different U
图4. (a) V原子的原子布居数随U值的变化曲线,(b) V-V键的重叠布居数随U值的变化曲线

Figure 5. The partial density of states (PDOS) of V ions d-orbital in monoclinic VO2 with different U
图5. U取不同的值时,V-3d轨道的分态密度(PDOS)图
较图6和图7所示的自旋极化态密度图我们认为VO2的金属绝缘体相变并不是Mott型而是电荷转移型。
4. 总结
本文采用基于密度泛函理论的第一性原理计算方法,分别计算了二氧化钒的Mulliken布居、能带结构以及电子态密度,解释了一些实验现象并对金属绝缘体相变作了一定的解释。结果得出如下结论:
首先,重叠布居数与原子间的距离相关而并不受占位库仑相互作用的影响。高的重叠布居值说明此键是共价键,而较低的重叠布居值说明是离子相互作用。计算分析发现R和M1相VO2中V-O的平均重叠布居值的比值为1.5,说明R相中V-O的共价性比M1相中的强。
其次,我们发现,随着U值得增加,不管在高温R相还是低温M1相的二氧化钒中都可以得到绝缘体态。然而在M1相中,能隙的突然打开现象与实验观测现象非常一致。另外,M1相VO2是带隙约为0.32 eV的间接带隙半导体,这个带隙值可以用来解释实验中突然观测到0.31 eV处发生光传输的现象。
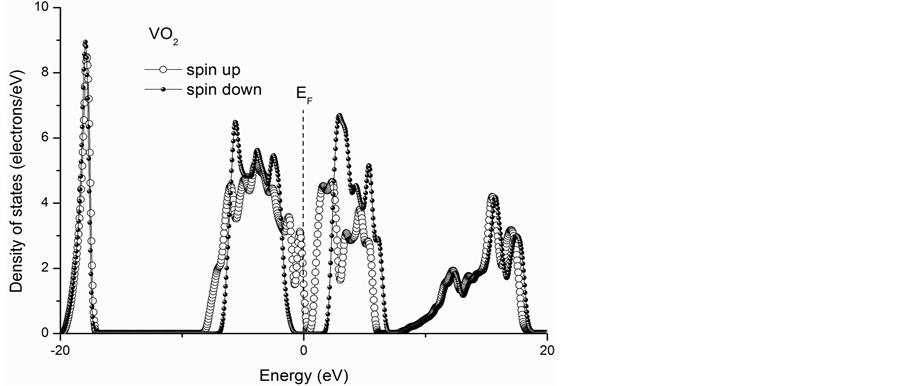
Figure 6. The spin polarized DOS of the insulating VO2
图6. 绝缘体特性VO2的自旋极化态密度
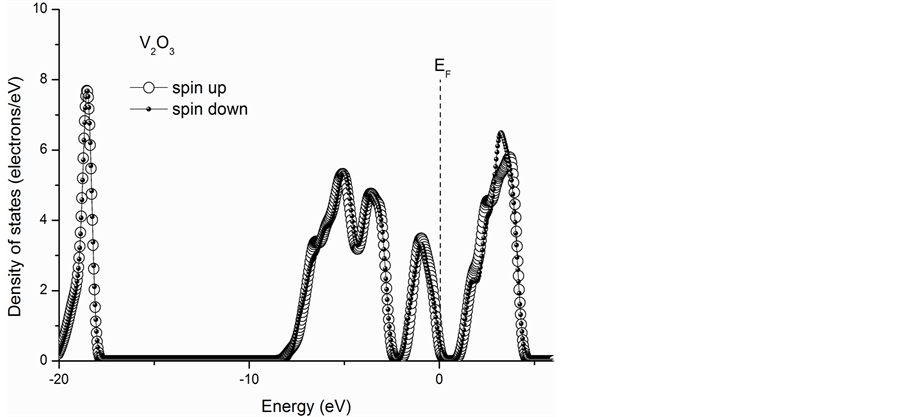
Figure 7. The spin polarized DOS of the insulating V2O3
图7. V2O3的自旋极化态密度
然而,直接带隙(~0.58 eV)可以解释实验中在0.6 eV处的光传输现象。由此,我们认为M1相中发生的MIT是一阶相变,并且并没有引起SPT。但是通过Mulliken布居分析,我们发现在MIT过程中,中心钒原子和其周边的6个氧配位体之间发生了一个有趣的电荷转移现象。这一现象表明二氧化钒中发生的金属绝缘体相变应该属于电荷转移型。
最后,由自旋极化态密度,我们研究了VO2的磁性特征。一般情况下,Mott型绝缘体(例如典型的V2O3)呈现反铁磁性,但是VO2却表现出铁磁特性。所以,我们认为VO2的金属绝缘体相变并不是Mott型即Mott-Hubbard机制,而是属于电荷转移型相变。
基金项目
国家自然科学基金(批准号:11347008)资助的课题。
文章引用
孔龙娟,刘光华,强凌. 二氧化钒电荷转移型金属绝缘体相变及电学性质研究
Charge-Transfer Metal-Insulator Transitions and Electronic Properties in Vanadium Dioxide[J]. 凝聚态物理学进展, 2015, 04(04): 119-127. http://dx.doi.org/10.12677/CMP.2015.44014
参考文献 (References)
- 1. Mott, N.F. (1968) Metal-Insulator Transition. Reviews of Modern Physics, 40, 677-683. http://dx.doi.org/10.1103/RevModPhys.40.677
- 2. Adler, D. (1968) Mechanisms for Metal-Nonmental Transitions in Transition-Metal Oxides and Sulfides. Reviews of Modern Physics, 40, 714-736. http://dx.doi.org/10.1103/RevModPhys.40.714
- 3. Shin, S., Suga, S., Taniguchi, M., Fujisawa, M., Kanzaki, H., Fujimori, A., Daimon, H., Ueda, Y., Kosuge, K. and Kachi, S. (1990) Vacuum-Ultraviolet Reflectance and Photoemission Study of the Metal-Insulator Phase Transitions in VO2, V6O13, and V2O3. Physical Review B, 41, Article ID: 4993. http://dx.doi.org/10.1103/PhysRevB.41.4993
- 4. Bermudez, V.M., Williams, R.T., Long, J.P., Reed, R.K. and Klein, P.H. (1992) Photoemission Study of Hydrogen Adsorption on Vanadium Dioxide near the Semiconductor-Metal Phase Transition. Physical Review B, 45, Article ID: 9266. http://dx.doi.org/10.1103/PhysRevB.45.9266
- 5. Uozumi, T., Okada, K. and Kotani, A.J. (1993) Electronic structures of Ti and V Oxides: Calculation of Valence Photoemission and Bremsstrahlung Isochromat Spectra. Journal of the Physical Society of Japan, 62, 2595-2599. http://dx.doi.org/10.1143/jpsj.62.2595
- 6. Goering, E., Schramme, M., Müller, O., Barth, R., Paulin, H., Klemm, M., Denboer, M.L. and Horn, S. (1997) LEED and Photoemission Study of the Stability of VO2 Surfaces. Physical Review B, 55, Article ID: 4225. http://dx.doi.org/10.1103/PhysRevB.55.4225
- 7. Kim, H.T., Chae, B.G., Youn, D.H., Maeng, S.L., Kim, G., Kang, K.Y. and Lim, Y.S. (2004) Mechanism and Observation of Mott transition in VO2-Based Two-And Three-Terminal Devices. New Journal of Physics 6, 52. http://dx.doi.org/10.1088/1367-2630/6/1/052
- 8. Kim, H.T., Chae, B.G., Youn, D.H., Lee, S.J., Kim, K. and Lim, Y.S. (2005) Raman Study of Electric-Field-Induced First-Order Metal-Insulator Transition in VO2-Based Devices. Applied Physics Letters, 86, 242101. http://dx.doi.org/10.1063/1.1941478
- 9. Kim, B.J., Lee, Y.W., Choi, S., Lim, J.W., Yun, S.J., Kim, H.T., Shin, T.J. and Yun, H.S. (2008) Micrometer X-Ray Diffraction Study of VO2 Films: Separation between Metal-Insulator Transition and Structural Phase Transition. Physical Review B, 77, Article ID: 235401.
- 10. Eguchi, R., Taguchi, M., Matsunami, M., Horiba, K., Yamamoto, K., Ishida, Y., Chainani, A., Takata, Y. and Yabashi, M. (2008) Photoemission Evidence for a Mott-Hubbard Metal-Insulator Transition in VO2. Physical Review B, 78, Article ID: 075115.
- 11. Goodenough, J.B. (1960) Direct Cation—Cation Interactions in Several Oxides. Physical Review, 117, 1442-1451. http://dx.doi.org/10.1103/PhysRev.117.1442
- 12. Caruthers, E., Kleinman, L. and Zhang, H.I. (1973) Energy Bands of Metallic VO2.. Physical Review B, 7, 3753-3760. http://dx.doi.org/10.1103/PhysRevB.7.3753
- 13. Zylbersztejn, A. and Mott, N.F. (1975) Metal-Insulator Transition in Vanadium Dioxide. Physical Review B, 11, 4383- 4395. http://dx.doi.org/10.1103/PhysRevB.11.4383
- 14. Sommers, C., De Groot, R., Kaplan, D. and Zylbersztejn, A. (1975) Cluster Calculations of the Electronic D-States in VO2. Journal de Physique Lettres, 36, 157-160. http://dx.doi.org/10.1051/jphyslet:01975003605015700
- 15. Wentzcovitch, R.M., Schulz, W.W. and Allen, P.B. (1994) VO2: Peierls or Mott-Hubbard? A View from Band Theory. Physical Review Letters, 72, 3389-3392. http://dx.doi.org/10.1103/PhysRevLett.72.3389
- 16. Rice, T.M., Launois, H. and Pouget, J.P. (1994) Comment on “VO2: Peierls or Mott-Hubbard? A View from Band Theory”. Physical Review Letters, 73, Article ID: 3042. http://dx.doi.org/10.1103/PhysRevLett.73.3042
- 17. Huang, X.Y., Yang, W.D. and Eckern, U. (1998) Met-al-Insulator Transition in VO2: A Peierls-Mott-Hubbard Mechanism. http://arxiv.org/abs/cond-mat/9808137
- 18. Biermann, S., Poteryaev, A., Lichtenstein, A.I. and Georges, A. (2005) Dynamical Singlets and Correlation-Assisted Peierls Transition in VO2. Physical Review Letters, 94, Article ID: 026404. http://dx.doi.org/10.1103/PhysRevLett.94.026404
- 19. Sakuma, R., Miyake, T. and Aryasetiawan, F. (2008) First-Principles Study of Correlation Effects in VO2. Physical Review B, 78, Article ID: 075106. http://dx.doi.org/10.1103/PhysRevB.78.075106
- 20. Morin, F.J. (1959) Oxides Which Show a Metal-to-Insulator Transition at the Neel Temperature. Physical Review Letters, 3, 34-36. http://dx.doi.org/10.1103/PhysRevLett.3.34
- 21. Boyce, J.B., Bridges, F.G., Claeson, T., Geballe, T.H., Li, G.G. and Sleight, A.W. (1991) Local Structure of BaBixPb1−xO3 Determined by X-Ray-Absorption Spectroscopy. Physical Review B, 44, 6961-6972. http://dx.doi.org/10.1103/PhysRevB.44.6961
- 22. Kim, H.T. (2000) Extension of the Brinkman-Rice Picture and the Mott Transition. Physica C: Superconductivity, 341, 259-260. http://dx.doi.org/10.1016/S0921-4534(00)00469-X
- 23. Brinkman, W.F. and Rice, T.M. (1970) Application of Gutzwiller’s Variational Method to the Metal-Insulator Transition. Physical Review B, 2, 4302-4304. http://dx.doi.org/10.1103/PhysRevB.2.4302
- 24. Laad, M.S., Craco, L. and Müller-Hartmann, E. (2006) Met-al-Insulator Transition in Rutile-Based VO2. Physical Review B, 73, Article ID: 195120. http://dx.doi.org/10.1103/PhysRevB.73.195120
- 25. Arcangeletti, E., Baldassarre, L., Di Castro, D., Lupi, S., Malavasi, L., Marini C., Perucchi, A. and Postorino, P. (2007) Evidence of a Pressure-Induced Metallization Process in Monoclinic VO2. Physical Review Letters, 98, Article ID: 196406. http://dx.doi.org/10.1103/PhysRevLett.98.196406
- 26. Segall, M.D., Lindan, P.L.D., Probert, M.J., Pickard, C.J., Hasnip, P.J., Clark, S.J. and Payne, M.C. (2002) First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. Journal of Physics: Condensed Matter, 14, 2717-2744. http://dx.doi.org/10.1088/0953-8984/14/11/301
- 27. Perdew, J.P. and Wang, Y. (1992) Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Physical Review B, 45, 13244-13249. http://dx.doi.org/10.1103/PhysRevB.45.13244
- 28. Hammer, B., Hansen, L.B. and Norskov, J.K. (1999) Im-proved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Physical Review B, 59, 7413-7421. http://dx.doi.org/10.1103/PhysRevB.59.7413
- 29. Monkhorst, H.J. and Pack, J.D. (1976) Special Points for Brillouin-Zone Integrations. Physical Review B, 13, 5188- 5192. http://dx.doi.org/10.1103/PhysRevB.13.5188
- 30. McWhan, D.B., Marezio, M., Remeika, J.P. and Dernier, P.D. (1974) X-Ray Diffraction Study of Metallic VO2. Physical Review B, 10, 490-495. http://dx.doi.org/10.1103/PhysRevB.10.490
- 31. Longo, J.M. and Kierkegaard, P. (1970) A Refinement of the Structure of VO2. Acta Chemica Scandinavica, 24, 420- 426. http://dx.doi.org/10.3891/acta.chem.scand.24-0420
- 32. Verleur, H.W., Barker Jr., A.S. and Berglund, C.N. (1968) Optical Properties of VO2 between 0.25 and 5 eV. Physical Review, 172, 788-798. http://dx.doi.org/10.1103/PhysRev.172.788
- 33. Ladd, L.A. and Paul, W. (1969) Optical and Transport Properties of High Quality Crystals of V2O4 near the Metallic Transition Temperature. Solid State Communications, 7, 425-428. http://dx.doi.org/10.1016/0038-1098(69)90888-6
- 34. Koethe, T.C., Hu, Z., Haverkort, M.W., Schüßler-Langeheine, C., Venturini, F., Brookes, N.B., Tjernberg, O., Reichelt, W., Hsieh, H.H., Lin, H.J., Chen, C.T. and Tjeng, L.H. (2006) Transfer of Spectral Weight and Symmetry across the Metal-Insulator Transition in VO2. Physical Review Letters, 97, Article ID: 116402. http://dx.doi.org/10.1103/PhysRevLett.97.116402
- 35. Chung, W. and Freericks, J.K. (1998) Charge-Transfer Metal-Insulator Transitions in the Spin-12 Falicov-Kimball Model. Physical Review B, 57, 11955-11961. http://dx.doi.org/10.1103/PhysRevB.57.11955
- 36. Marezio, M., McWhan, D.B., Dernier, P.D. and Remeika, J.P. (1972) Charge Localization at Metal-Insulator Transitions in Ti4O7 and V4O7. Physical Review Letters, 28, 1390-1393. http://dx.doi.org/10.1103/PhysRevLett.28.1390
- 37. Avci, R. and Flynn, C.P. (1978) Charge-Transfer Insulators. Physical Review Letters, 41, 428-431. http://dx.doi.org/10.1103/PhysRevLett.41.428
- 38. Hague, C.F., Mariot, J.M., Ilakovac, V. and Delaunay, R. (2008) Charge Transfer at the Metal-Insulator Transition in V2O3 Thin Films by Resonant Inelastic X-Ray Scatterin. Physical Review B, 77, Article ID: 045132. http://dx.doi.org/10.1103/PhysRevB.77.045132