Artificial Intelligence and Robotics Research
Vol.05 No.02(2016), Article ID:17674,6
pages
10.12677/AIRR.2016.52004
Comparison of Classic Algorithm for Orientation Estimation
Dalong Li
Qingdao Branch of Naval Aeronautical Engineering Institute, Qingdao Shandong

Received: May 6th, 2016; accepted: May 24th, 2016; published: May 27th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Orientation estimation aims to compute the orientation angles of multi-dimensional signals and can be applied to many basic tasks in image processing and computer vision. In this paper, a short review of existing methods for estimating local orientation tensors has been given and error comparison was done to facilitate further research work and to design more accurate orientation estimation methods.
Keywords:Orientation Estimation, Image Processing, Error Comparison

典型方向估计方法比较研究
李大龙
海军航空工程学院青岛校区,山东 青岛

收稿日期:2016年5月6日;录用日期:2016年5月24日;发布日期:2016年5月27日

摘 要
方向估计的主要目的是计算出图像等多维信号各点的方向信息,在图像处理和机器视觉的底层处理中具有广泛的应用。在总结现有的方向估计方法的基础上,对现有方法进行了误差比较,从而有利于对这类方法进行深入研究或设计更准确的方向估计方法。
关键词 :方向估计,图像处理,误差比较

1. 引言
方向估计可以计算出图像中各点的方向信息,在边缘提取、图像分割、纹理分析、自适应滤波、立体视差估计、图像增强和运动分析中都有直接应用,对位移和光流场的计算即对信号在三维空间中进行方向估计。如果把图像处理分为三个层次:底层视觉、中层视觉和高层视觉,那么底层视觉的主要任务就是提取不同尺度下的边缘及其方向信息。
本文的主要工作是对现有的方向估计方法进行分类总结,并进行误差比较,从而有利于对这类方法进行进一步研究。
2. 相关工作
现有的方向估计方法根据方向表示法来划分,可以分为基于通道表示的方法、基于自相关函数的方法和基于张量的方法。下面本文采用后一种分类方法对相关工作分别介绍。
2.1. 分类概述
基于通道表示的方法 [1] 选择某种核函数对信号在不同尺度下的梯度分别作一个映射,然后通过对该核函数的编解码过程来估计方向。现有的方法中,核函数主要有两种:一种是高斯函数;另一种是余弦函数。
基于自相关函数的方法 [2] [3] 主要基于信号理论以及对方向概念的统计分析。这种估计方法与其它方法相比,无需直接计算灰度梯度,而是直接计算信号的自相关函数,然后用抛物线拟合自相关函数的一小部分中心值并从抛物线的主曲率的方向中推导出所要估计的方向。信号对频域中信噪比的适应性通过对自相关函数进行线性滤波获得。
基于张量的方法 [4] - [19] 用二阶张量表示方向,表示方法简单有效,是目前应用最为广泛的一种方法。与前两种方法相比,这类方法具有实现简单、计算复杂度低等优点,因而论文重点对这类方法进行了研究。
2.2. 基于张量的方法
根据(方向)张量的计算方法不同,这类方法可以进一步细分为梯度张量法 [4] - [12] 、多项式张量法 [13] 和正交张量法 [14] - [19] 。Bjorn Johansson和 Gunnar Farneback [23] 对不同的方向张量计算方法进行了比较。
梯度张量法与以往一些文献中提到的结构张量(Structure Tensor)的计算方法相同,主要是采用某种微分算子计算图像的灰度梯度,然后根据不同方向的梯度构造张量,这类方法的主要缺点是对噪声的鲁棒性比较差,往往需要一个整体上的平滑,而这一平滑过程使得方向估计的局部特征受到全局特征的干扰。文献 [24] 比较了窗口傅里叶变换法和边缘梯度方法在解决边缘方向估计问题中优劣。基于梯度张量的方法中,S. Fu等 [4] 加入均值滤波平滑噪声;A. Shrivastava [5] 和Davide Maltoni [6] 采用计算二倍角的方法克服正切变换在90度附近的不连续性和三角函数及角度的周期性的影响;Kuldeep Singh等 [7] 引入主元分析与多分辨率Kalman滤波提高估计结果的精度和鲁棒性;I.V. Grigoryeva等 [8] 主要讨论了多方向估计的问题;J. Feng [9] 和A. Sourice [10] 对梯度算子进行了改进,改善了一些轮廓关键点的方向估计结果;Jie Zhou等 [11] 先采用梯度梯度张量进行粗略估计,然后通过多项式模型优化方向估计结果;S. Kim等 [12] 提出了ABFT框架,由噪声鲁棒的特征检测和仿射不变量的二进制特征描述基于结构张量空间。
基于多项式张量的方法 [13] 是采用正则化卷积(Normalized Convolution)的信号分析方法,综合考虑信号的不确定性和信号分析函数,首先选择一组信号分析函数构成一组基,然后通过正则化卷积获得这组基的系数,这组系数与信号的泰勒展开式具有对应关系,最后采用多项式近似构造方向张量。正则化卷积的方法最初由Knutsson和Westin [20] - [22] 提出,其几何解释是:将信号及其邻域投影到一个由信号分析函数张成的子空间。其投影过程等同于一个加权最小均方问题,其权值由信号的确定性和分析函数决定。每一点的卷积结果是对应于分析函数的展开系数。尽管最小均方估计、选取分析函数及处理数据的不确定性都不是新思想,正则化卷积的创新之处在于将三者有效结合于统一的理论框架下。
基于正交张量的方法一般是设计一组正交滤波器,在频域对信号进行滤波,最后根据滤波器组的输出结果构造方向张量,用于估计方向。G. H. Granlund和H. Knutsson [14] 提出了一种基于lognormal滤波器(一种极坐标下可分解的正交滤波器)的方向估计方法;Tsantis Stavros等 [15] 使用EFCM聚类分析方法和多分辨力小波分析从散斑噪声中区分图像的边缘问题;Hans Knutsson等 [16] 主要采用单项式形式的傅里叶定向成对滤波器组,一个奇数阶集和一个偶数阶集,以实现相不变半正定局部结构张量估计;Fatih Porikli [17] 主要针对彩色图像进行了颜色信息的融合处理;C. Gottschlich [18] 和Hao Geng [19] 采用Gabor滤波器获得方向信息;Ryan P [25] 通过对正交滤波得到的方向角度图进行扩散滤波提高估计的鲁棒性。
2.3. 比较与分析
我们选取了几种比较典型的方法进行比较,它们是基于通道表示的方法、基于梯度的方法、基于正交滤波的方法、基于正则化卷积的方法和基于Gabor滤波的方法。
通过对已知方向信息的合成图像进行方向估计,可以得到不同方法对各种倾角的直线进行方向估计的平均误差。这里,合成图像由各种倾角的直线组成,选取对各种倾角的直线进行估计的原因是不同倾角的直线离散化的误差不同,只有某些特定的方向(如水平、垂直和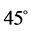 方向)不存在离散化误差。其中,平均误差的计算公式为:
方向)不存在离散化误差。其中,平均误差的计算公式为:
 (1)
(1)
式中,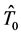 为方向张量的准确值,
为方向张量的准确值,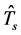 为估计值对应的张量。对于基于通道表示的方法需要将估计结果转化成张量表示。另外需要指出的是,这一误差的计算方法与方向角之间不存在直接的对应关系,只是误差大小的一个衡量标准。
为估计值对应的张量。对于基于通道表示的方法需要将估计结果转化成张量表示。另外需要指出的是,这一误差的计算方法与方向角之间不存在直接的对应关系,只是误差大小的一个衡量标准。
表1为对几种不同方向估计方法的估计误差进行计算的实验数据,而图1和图2为根据实验数据绘制的误差比较图。首先,从估计精度角度看,在无噪的情况下,前四种方法的估计误差都比较小,而第五种方法的估计精度受滤波器个数的影响,随滤波器个数的增加而减小。其次,从对噪声的鲁棒性角度看,随着噪声的增加,基于梯度的方法受影响最大;基于正则化卷积的方法次之;基于Gabor的方法在对噪声的鲁棒性方面同样受滤波器个数的影响比较大;基于通道表示的方法在噪声较小时鲁棒性还好,当噪声增大到一定程度时估计误差也会明显增大;基于正交滤波的方法不但估计误差较小,对噪声的鲁棒性也最好;从图2的误差变动曲线中更可以看出基于正交滤波的方法的优越性。第三,进一步从计算
复杂度分析,对于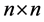 大小的图像,原始算法的计算复杂度为
大小的图像,原始算法的计算复杂度为 ,其中,对图像作Fourier变换
,其中,对图像作Fourier变换
Table 1. The error comparison of some orientation estimation methods
表1. 几种方向估计方法的误差比较

Figure 1. The estimation error histogram of each orientation estimation
图1. 各方向估计方法的估计误差柱状图
的计算复杂度为 ;计算滤波函数矩阵的计算复杂度为
;计算滤波函数矩阵的计算复杂度为 ;对单个图像象素点进行方向张量的特征值分解的计算复杂度为
;对单个图像象素点进行方向张量的特征值分解的计算复杂度为 ,所以对于整幅图像计算复杂度为
,所以对于整幅图像计算复杂度为 ,故整个算法的计算复杂度为
,故整个算法的计算复杂度为 。另外,基于正交滤波的方法采用张量表示方向,具有表示方法的简洁性,而且是唯一一种对于简单信号具有相位不变性的方向估计方法,所以,综合考虑估计精度、对噪声的鲁棒性、计算复杂度等因素,基于正交滤波的方法是比较好的方向估计方法。
。另外,基于正交滤波的方法采用张量表示方向,具有表示方法的简洁性,而且是唯一一种对于简单信号具有相位不变性的方向估计方法,所以,综合考虑估计精度、对噪声的鲁棒性、计算复杂度等因素,基于正交滤波的方法是比较好的方向估计方法。

Figure 2. The estimation error change curve of each orientation estimation method
图2. 各方向估计方法的估计误差变动曲线
3. 结束语
本文对现有的方向估计方法进行了分类总结和实验分析,从而可以看出各种方法对噪声的鲁棒性程
度。在此基础上,本文进一步对其中性能较好的两种方法:基于自相关函数的方法和基于正交滤波的方法进行了计算复杂度分析,从而可以看出基于正交滤波的方向估计方法的优越性。我们下一步的工作将对基于正交滤波的方法进行进一步的改进。
文章引用
李大龙. 典型方向估计方法比较研究
Comparison of Classic Algorithm for Orientation Estimation[J]. 人工智能与机器人研究, 2016, 05(02): 35-40. http://dx.doi.org/10.12677/AIRR.2016.52004
参考文献 (References)
- 1. Spies, H. and Forssén, P.-E. (2003) Two-Dimensional Channel Representation for Multiple Velocities, Image Analysis. Volume 2749 of the Series Lecture Notes in Computer Science, Springer, Berlin Heidelberg, 356-362.
- 2. Mester, R. (2000) Orientation Estimation: Conventional Techniques and a New Non-Differential Approach. Proceeding of the 10th European Signal Processing Conference, 2, 921-924.
- 3. Yang, X.D., Chau, W. and Wong, S.K.M. (1993) Multi-Scale Orientation Estimation for Unstructured Sample Points. IEEE CCGEI.
- 4. Fu, S. and Zhang, C. (2012) Fringe Pattern Denoising Using Averaging Based on Nonlocal Self-Similarity. Optics Communications, 285, 2541-2544. http://dx.doi.org/10.1016/j.optcom.2012.01.059
- 5. Shrivastava, A. and Srivastava, D.K. (2014) Fingerprint Identification Using Feature Extraction: A Survey. International Conference on Contemporary Computing and Informatics (IC3I), Mysore, 522-525. http://dx.doi.org/10.1109/ic3i.2014.7019653
- 6. Maltoni, D. and Maio, D. (2003) Handbook of Fingerprint Recognition. Springer, 85-91.
- 7. Singh, K., Kapoor, R. and Nayar, R. (2015) Fingerprint Denoising Using Ridge Orientation Based Clustered Dictionaries. Neurocomputing, 167, 418-423.
- 8. Grigoryeva, I.V. (2012) Segmentation Algorithm with Several Dominant Directions. 11th International Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, 16-18.
- 9. Feng, J., Zhou, J. and Jain, A.K. (2013) Orientation Field Estimation for Latent Fingerprint Enhancement. IEEE Trans- actions on Pattern Analysis and Machine Intelligence, 35, 925-940. http://dx.doi.org/10.1109/TPAMI.2012.155
- 10. Sourice, A., Plantier, G. and Saumet, J.L. (2003) Autocorrelation Fitting for Texture Orientation Estimation. International Conference on Image Processing.
- 11. Zhou, J. and Gu, J.W. (2004) A Model-Based Method for the Computation of Fingerprints’ Orientation Field. IEEE Transactions on Image Processing, 13, 821-835.
- 12. Kim, S., Yoo, H., Ryu, S., Ham, B. and Sohn, K. (2013) ABFT: Anisotropic Binary Feature Transform Based on Structure Tensor Space. 20th IEEE International Conference on Image Processing (ICIP), Melbourne, 2920-2923.
- 13. Yu, L., Tian, M.S. and Li, G. (2014) A Novel Video Super-Resolution Algorithm Based on Non-Local Normalized Convolution, Unifying Electrical Engineering and Electronics Engineering. Vol. 238 of the Series Lecture Notes in Electrical Engineering, 1141-1150.
- 14. Granlund, G.H. and Knutsson, H. (1995) Signal Processing for Computer Vision. Kluwer Academic Publishers. http://dx.doi.org/10.1007/978-1-4757-2377-9
- 15. Stavros, T., Stavros, S., et al. (2014) Multiresolution Edge Detection Using Enhanced Fuzzy c-Means Clustering for Ultrasound Image Speckle Reduction. Medical Physics, 41, Article ID: 072903. http://dx.doi.org/10.1118/1.4883815
- 16. Knutsson, H., Westin, C.-F. and Andersson, M. (2012) Structure Tensor Estimation: Introducing Monomial Quadrature Filter Sets. In: Laidlaw, D.H. and Vilanova, A., Eds., New Developments in the Visualization and Processing of Tensor Fields, Part of the Series Mathematics and Visualization, Springer, Berlin, 3-28. http://dx.doi.org/10.1007/978-3-642-27343-8_1
- 17. Lee, J.W. and Cho, J.S. (2009) Effective Lane Detection and Tracking Method Using Statistical Modeling of Color and Lane Edge-Orientation. 4th International Conference on Computer Sciences and Convergence Information Technology, ICCIT’09, Seoul, 24-26 November 2009, 1586-1591. http://dx.doi.org/10.1109/iccit.2009.81
- 18. Gottschlich, C. (2012) Curved-Region-Based Ridge Frequency Estimation and Curved Gabor Filters for Fingerprint Image Enhancement. IEEE Transactions on Image Processing, 21, 2220-2227. http://dx.doi.org/10.1109/TIP.2011.2170696
- 19. Geng, H., Li, J.C., Zhou, J.W. and Chen, D. (2015) An Improved Gabor Enhancement Method for Low-Quality Fingerprint Images. AOPC 2015: Image Processing and Analysis, Proceedings of the SPIE, 9675, Article ID: 96751J.
- 20. Westin. C.-F. (1994) A Tensor Framework for Multidimensional Signal Processing. SE-581 83, Dissertation No. 348, PhD Thesis, Linkoping University, Linkoping.
- 21. Knutsson, H., Westin, C.-F. and Westelius, C.-J. (1993) Filtering of Uncertain Irregularly Sampled Multidimensional Data. 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 1-3 November 1993, 1301-1309. http://dx.doi.org/10.1109/ACSSC.1993.342325
- 22. Knutsson, H. and Westin, C.-F. (1993) Normalized and Differential Convolution: Methods for Interpolation and Filtering of Incomplete and Uncertain Data. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, 15-17 Jun 1993, 515-523. http://dx.doi.org/10.1109/cvpr.1993.341081
- 23. Johansson, B. and Farneback, G. (2002) A Theoretical Comparison of Different Orientation Tensors. Proceedings SSAB02 Symposium on Image Analysis, Lund, March 2002, 69-73.
- 24. Wang, H.X. and Qian, K.M. (2012) Quality-Guided Orientation Unwrapping for Fringe Direction Estimation. Applied Optics, 51, 413-421. http://dx.doi.org/10.1364/AO.51.000413
- 25. Cabeen, R.P., Bastin, M.E. and Laidlaw, D.H. (2016) Kernel Regression Estimation of Fiber Orientation Mixtures in Diffusion MRI. Neuroimage, 127, 158-172. http://dx.doi.org/10.1016/j.neuroimage.2015.11.061
