Advances in Applied Mathematics
Vol.03 No.02(2014), Article ID:13471,7
pages
10.12677/AAM.2014.32009
Explicit Computations of Hopf and Bautin Bifurcations in  -Symmetric Systems
-Symmetric Systems
Guojun Peng, Xianfa Fu
School of Computer Science, Guangdong Polytechnic Normal University, Guangzhou
Email: pgjatsin@sina.com
Received: Mar. 20th, 2014; revised: Apr. 21st, 2014; accepted: Apr. 29th, 2014
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
By using a homogical method, we drive out computational formulae for normal forms of the Hopf and Bautin bifurcations in 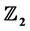 -symmetric systems. For practical bifurcation analysis of Hopf and Bautin in a
-symmetric systems. For practical bifurcation analysis of Hopf and Bautin in a  -symmetric system, we can use these formulae to compute the first and the second Lyapunov coefficients, and check whether the bifurcation is degenerate. Furthermore, we can use the formulae of unfolding parameters to decide the topological structures when parameters perturb in a neighborhood of the critical values. So, we construct the relation between the parameters and the structures for Hopf and Bautin bifurcations in any
-symmetric system, we can use these formulae to compute the first and the second Lyapunov coefficients, and check whether the bifurcation is degenerate. Furthermore, we can use the formulae of unfolding parameters to decide the topological structures when parameters perturb in a neighborhood of the critical values. So, we construct the relation between the parameters and the structures for Hopf and Bautin bifurcations in any 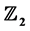 -symmetric systems.
-symmetric systems.
Keywords:Hopf Bifurcation, Bautin Bifurcation,  -Symmetric, Normal Form, Homogical Method
-Symmetric, Normal Form, Homogical Method

显式计算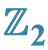 对称系统的Hopf和Bautin分岔
对称系统的Hopf和Bautin分岔
彭国俊,傅仙发
广东技术师范学院计算机科学学院,广州
Email: pgjatsin@sina.com
收稿日期:2014年3月20日;修回日期:2014年4月21日;录用日期:2014年4月29日

摘 要
本文用同调方法导出任意维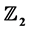 对称系统的Hopf和Bautin分岔规范型的计算公式。在对实际
对称系统的Hopf和Bautin分岔规范型的计算公式。在对实际 对称系统进行Hopf和Bautin分岔分析时,可以直接利用这些公式来计算第一和第二Lyapunov系数,从而判断对应分岔是否退化。进一步地,还可以利用开折参数的计算公式来确定系统参数在临界值附近扰动时,对应的拓扑结构。因此,实际建立了任意维
对称系统进行Hopf和Bautin分岔分析时,可以直接利用这些公式来计算第一和第二Lyapunov系数,从而判断对应分岔是否退化。进一步地,还可以利用开折参数的计算公式来确定系统参数在临界值附近扰动时,对应的拓扑结构。因此,实际建立了任意维 对称系统Hopf和Bautin分岔的参数和其结构之间的对应关系。
对称系统Hopf和Bautin分岔的参数和其结构之间的对应关系。
关键词 :Hopf分岔,Bautin分岔, 对称,规范型,同调方法
对称,规范型,同调方法

1. 引言
规范型方法是研究微分方程定性和分岔(尤其是动态分岔)的重要工具。在分岔分析中,若能将系统的某种分岔约化至其对应的规范型,就可以知道系统的结构。下面考虑如下的含参系统:
 (1.1)
(1.1)
其中, ,
, ,
, 充分光滑。先考虑参数维
充分光滑。先考虑参数维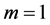 的情形。假设(1.1)在
的情形。假设(1.1)在 时有平衡点
时有平衡点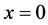 ,并且其雅可比矩阵在
,并且其雅可比矩阵在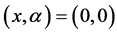 有一对共轭虚数特征值
有一对共轭虚数特征值 ,此外再没有实部为零的特征值(临界特征值)。此时,当
,此外再没有实部为零的特征值(临界特征值)。此时,当 在0附近扰动时,若(1.1)发生Hopf分岔,其规范型为[1] [2] :
在0附近扰动时,若(1.1)发生Hopf分岔,其规范型为[1] [2] :
 (1.2)
(1.2)
其中 和
和 是在
是在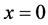 附近限制在分岔中心流形上的状态变量,分岔发生的条件为:第一Lyapunov系数
附近限制在分岔中心流形上的状态变量,分岔发生的条件为:第一Lyapunov系数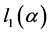 满足
满足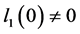 (非退化)和
(非退化)和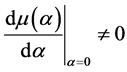 (横截性)。若引入
(横截性)。若引入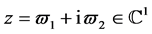 ,则得到如下的复规范型:
,则得到如下的复规范型:
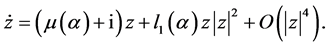 (1.3)
(1.3)
引入复变量 ,由高阶项不影响平衡点附近的拓扑结构,(1.3)可化为截断规范型 [1] [2] :
,由高阶项不影响平衡点附近的拓扑结构,(1.3)可化为截断规范型 [1] [2] :
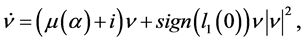 (1.4)
(1.4)
从而可以通过上面标准规范型的分岔图 [3] (如图1),获得(1.3)在对应参数下的结构。
若 ,则Hopf分岔退化为余维
,则Hopf分岔退化为余维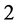 以上的情形,对应余维
以上的情形,对应余维 情形的Bautin分岔的规范型为 [1] [2] :
情形的Bautin分岔的规范型为 [1] [2] :
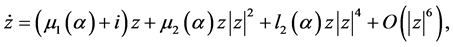 (1.5)
(1.5)
此时参数维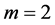 ,
,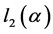 为第二Lyapunov系数,余维
为第二Lyapunov系数,余维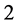 分岔发生的条件为:
分岔发生的条件为: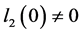 ,
, 。若引入复变量
。若引入复变量 ,由(1.5)可得到如下的截断规范型:
,由(1.5)可得到如下的截断规范型:
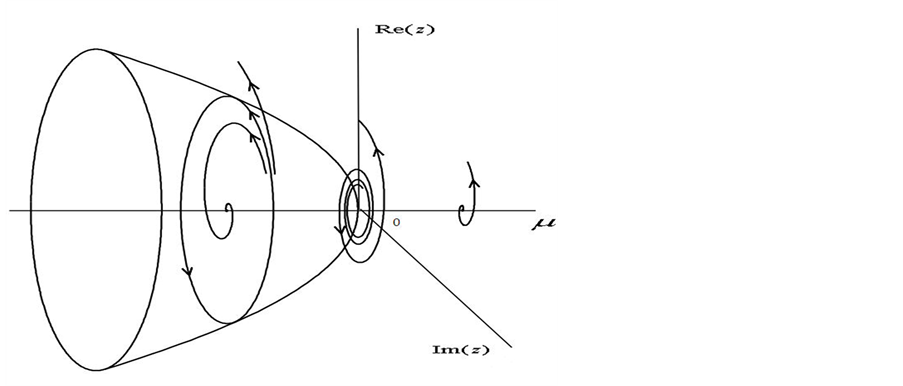
Figure 1. Hopf bifurcation diagram of (1.4) with 
图1. 系统(1.4)的Hopf分岔图,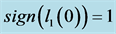
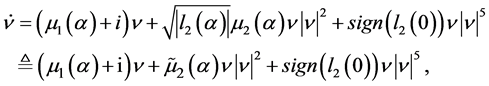 (1.6)
(1.6)
从而可以通过上面标准规范型的分岔图 [3] [4] (如图2),获得(1.5)在对应参数下的结构。
附注1:若给定系统的临界参数或平衡点不为0,可以通过参数或变量平移,使其具有(1)的形式。
附注2:对于本文所考虑的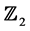 对称系统之特殊情形,规范型(1.2),(1.3)和(1.4)最后余项的指数应相应增加
对称系统之特殊情形,规范型(1.2),(1.3)和(1.4)最后余项的指数应相应增加 。
。
关于规范型(1.3)和(1.4)中临界Lyapunov系数 和
和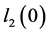 的计算,已有相关结果发表 [4] - [6] 。但对其中开折参数
的计算,已有相关结果发表 [4] - [6] 。但对其中开折参数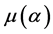 ,
, 和
和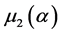 的计算公式却很少见。鉴于
的计算公式却很少见。鉴于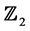 对称系统的特殊性,本文作者在文献 [7] 中给出了余维
对称系统的特殊性,本文作者在文献 [7] 中给出了余维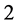 的Takens-Bogdanov分岔开折参数的显式计算公式,而在本文中给出Hopf和Bautin分岔临界规范型系数以及开折参数的显式计算公式。
的Takens-Bogdanov分岔开折参数的显式计算公式,而在本文中给出Hopf和Bautin分岔临界规范型系数以及开折参数的显式计算公式。
2. 临界规范型系数的计算公式
引理2.1 [3] :复系统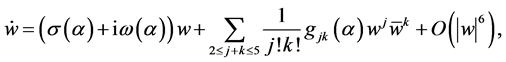 其中
其中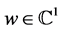 ,
, ,
, 或2,
或2,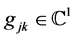 ,
,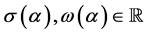 ,且
,且 ,
,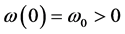 ,能够通过光滑依赖于参数的可逆复坐标变换(对充分小的
,能够通过光滑依赖于参数的可逆复坐标变换(对充分小的 ):
):
 (2.1)
(2.1)
约化为下面仅含有共鸣项的系统:
 (2.2)
(2.2)
其中,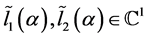 。
。
系统(1.1) 在临界情形下,由其 对称性,右端可如下展开:
对称性,右端可如下展开:
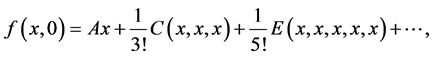 (2.3)
(2.3)
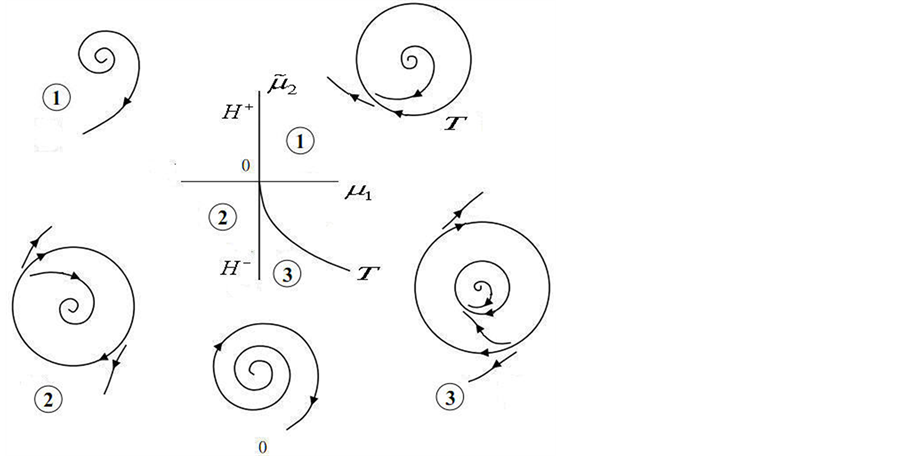
Figure 2. Bautin bifurcation diagram of (1.6) with ,
, ,
, 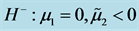 ,
, 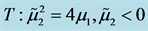
图2. 系统(1.6)的Bautin分岔图, ,
,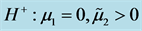 ,
, ,
,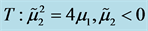
其中, ,
, ,
,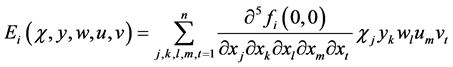 ,
, 。在
。在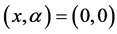 时,由(1.1)仅有一对虚数临界特征值
时,由(1.1)仅有一对虚数临界特征值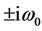 ,存在特征向量
,存在特征向量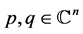 满足:
满足:
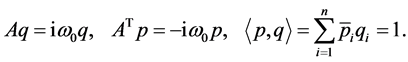
定理 1 系统(1.1)相应于Hopf和Bautin分岔的第一和第二Lyapunov系数的临界值计算公式分别为:
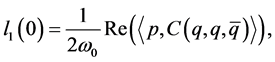 (2.4)
(2.4)
 (2.5)
(2.5)
其中, 和
和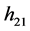 可分别通过如下的线性方程来解出:
可分别通过如下的线性方程来解出:

证明:记 为由
为由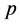 和
和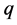 所生成的临界特征空间。在此临界情形下,将(1.1)限制在2维不变中心流形
所生成的临界特征空间。在此临界情形下,将(1.1)限制在2维不变中心流形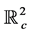 上:
上:
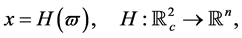 (2.6)
(2.6)
从而受限系统为:
 (2.7)
(2.7)
将(2.6)和(2.7)代入(1.1)的临界方程 得到同调方程:
得到同调方程:
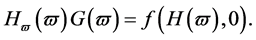 (2.8)
(2.8)
另一方面,任意向量 都可以表示为:
都可以表示为:
 (2.9)
(2.9)
将(2.9)代入(2.8),同调方程成为:
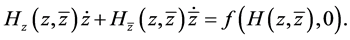 (2.10)
(2.10)
再将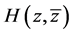 展开如下:
展开如下:
 (2.11)
(2.11)
其中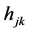 待定。根据引理2.1,
待定。根据引理2.1,
 ,将其连同(2.11)代入(2.10),并将(2.10)的右端按(2.3)展开,比较两端
,将其连同(2.11)代入(2.10),并将(2.10)的右端按(2.3)展开,比较两端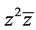 项的系数得到如下的奇线性方程:
项的系数得到如下的奇线性方程:

由于
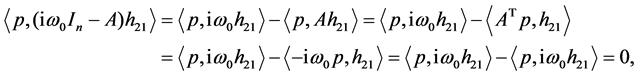
于是有
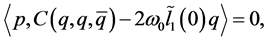
利用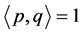 ,从而得到第一Lyapunov系数
,从而得到第一Lyapunov系数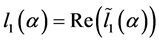 的临界值公式(2.4)。
的临界值公式(2.4)。
若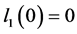 ,则需要计算第二Lyapunov系统来判断分岔余维是否为
,则需要计算第二Lyapunov系统来判断分岔余维是否为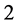 。此时,由引理2.1得到,
。此时,由引理2.1得到,
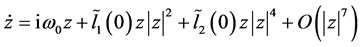 ,将其和(2.11)一起代入(2.10)后,通过比较两端
,将其和(2.11)一起代入(2.10)后,通过比较两端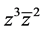 项的系数得奇线性方程:
项的系数得奇线性方程:
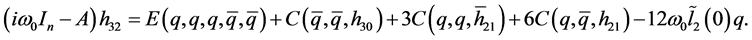
类似前面,通过将上面方程的两端共轭左乘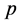 ,得到第二Lyapunov系数
,得到第二Lyapunov系数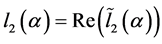 的临界值计算公式(2.5)。通过比较
的临界值计算公式(2.5)。通过比较 项的系数,得到求解
项的系数,得到求解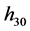 的线性方程:
的线性方程:
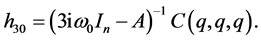
其中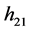 可通过解如下的扩展方程(
可通过解如下的扩展方程(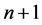 维)来确定:
维)来确定:

3. 广义开折参数的计算公式
下面将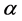 在临界参数值0附近扰动,并计算对应的开折参数
在临界参数值0附近扰动,并计算对应的开折参数 。设系统(1.1)此时的特征值为
。设系统(1.1)此时的特征值为 ,显然有
,显然有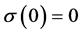 。相应于(2.3)的展开式为:
。相应于(2.3)的展开式为:
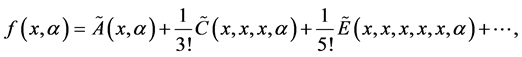 (3.1)
(3.1)
其中 ,
,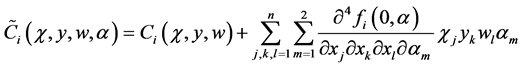 ,
,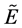 类似。此情形下,对于充分小的
类似。此情形下,对于充分小的 ,存在参数依赖的向量
,存在参数依赖的向量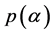 和
和 满足:
满足:
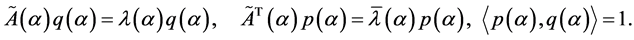
定理 2 系统(1.1)相应于Bautin分岔的开折参数的计算公式为:
 (3.2)
(3.2)
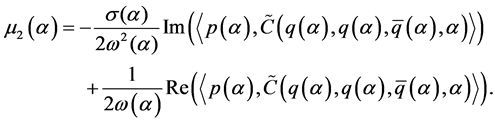 (3.3)
(3.3)
Hopf分岔的余维是 ,其规范型 (1.3)中的开折参数
,其规范型 (1.3)中的开折参数 。
。
证明:此情形下,与(2.10)相应的同调方程为:
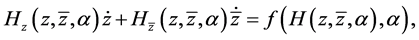 (3.4)
(3.4)
与(2.11)对应的展开形式则为:
 (3.5)
(3.5)
而且 满足引理2.1中的(2.2)。将(2.2),(3.5)代入(3.4),并按(3.1)展开,通过类似于前面的计算得到:
满足引理2.1中的(2.2)。将(2.2),(3.5)代入(3.4),并按(3.1)展开,通过类似于前面的计算得到:

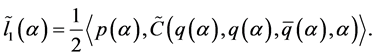
下面考虑将(2.2)化为规范型(1.3)的形式。引入时间变换
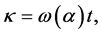 因为
因为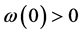 ,所以对于充分小的
,所以对于充分小的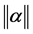 ,时间方向不变,(2.2)在此变换下成为:
,时间方向不变,(2.2)在此变换下成为:

注意到上面系统中非线性项系数为复数的情形,现引入新的时间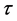 满足
满足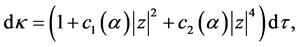
其中 待定,将上面的系统约化为:
待定,将上面的系统约化为:

当取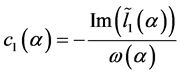 ,
,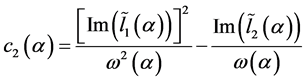 时,上面系统的非线性项系数为实数,从而化成了规范型(1.5),并且有:
时,上面系统的非线性项系数为实数,从而化成了规范型(1.5),并且有: 以及
以及

4. 应用实例
考虑如下改变van der Pol振子 [8]
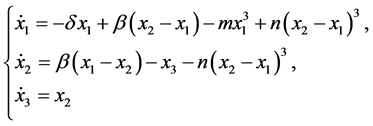 (4.1)
(4.1)
的Bautin分岔。容易验证:当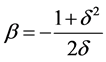 ,
, 时,(4.1)在平衡点
时,(4.1)在平衡点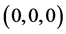 有特征值
有特征值 ,
, 。按(2.3)展开有:
。按(2.3)展开有: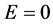
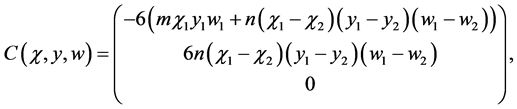 。规范化的临界特征向量计算为:
。规范化的临界特征向量计算为:
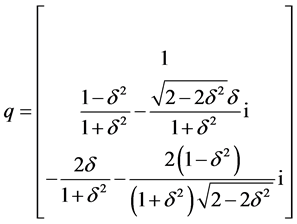 ,
,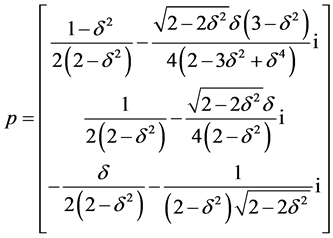 。
。
利用定理1的公式(2.4)立即得到 。若
。若 ,则Hopf分岔退化
,则Hopf分岔退化
为余维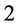 以上情形。此时,通过定理1的公式计算
以上情形。此时,通过定理1的公式计算 和
和 ,然后代入(2.5)直接得到:
,然后代入(2.5)直接得到:
 。
。
在临界值 附近扰动参数
附近扰动参数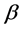 和
和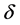 :
: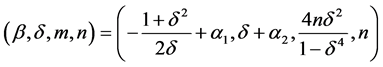 。
。
为精简起见,我们任取下面的参数值 ,
,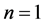 ,
, ,计算得:
,计算得:
 ,
,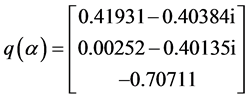 ,
,
 ,
, ,
,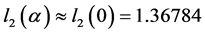 。再利
。再利
用定理2的公式(3.2)和(3.3)计算得到: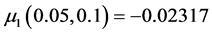 ,
, 。最后,计算(1.6)中的开折参数
。最后,计算(1.6)中的开折参数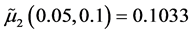 ,对照分岔图2知道,此时系统在分岔对应的二维中心流形上,其相图结构为②,在平衡点附近存在唯一不稳定的极限环。
,对照分岔图2知道,此时系统在分岔对应的二维中心流形上,其相图结构为②,在平衡点附近存在唯一不稳定的极限环。
项目基金
广东省自然科学基金(No.s2012040006688)和广东省教育厅科技创新项目(No.2012KJCX0073)资助。
文章引用
彭国俊,傅仙发, (2014) 显式计算Z2对称系统的Hopf和Bautin分岔
Explicit Computations of Hopf and
Bautin Bifurcations in Z2-Symmetric
Systems. 应用数学进展,02,54-61. doi: 10.12677/AAM.2014.32009
参考文献 (References)
- 1. Guckenheimer, J. and Holmes, P.J. (1983) Nonlinear oscillations, dynamical systems and bifurcations of vector fields. Springer, New York.
- 2. Chow, S.N., Li, C.Z. and Wang, D. (1994) Normal forms and bifurcation of planar vector fields. Cambridge University Press, Cambridge.
- 3. Kuznetsov, Yu.A. (2004) Elements of applied bifurcation theory. 3rd Edition, Springer, New York.
- 4. Hassard, B., Kazarinoff, N. and Wan, Y.H. (1981) Theory and applications of Hopf bifurcation. Cambridge University Press, London.
- 5. Kuznetsov, Yu.A. (1999) Numerical normalization techniques for all codim 2 bifurcations of equilibria in ODEs. SIAM Journal on Numerical Analysis, 36, 1104-1124.
- 6. Shilnikov, L.P., Shilnikov, A.L., Turaev, D.V. and Chua, L. (2001) Methods of qualitative theory in nonlinear dynam- ics. World Scientific, Singapore.
- 7. Peng, G.J. and Jiang, Y.L. (2013) Computation of universal unfolding of the double-zero bifurcation in -symmetric systems by a homological method. Journal of Difference Equations and Applications, 19, 1501-1512.
- 8. Freire, E., Rodríguez-Luis, A.J., Gamero, E. and Ponce, E. (1993) A case study for homoclinic chaos in an autonomous electronic circuit. A trip from Takens-Bogdanov to Hopf-Šil’nikov. Physica D, 62, 230-253.