Advances in Applied Mathematics
Vol.04 No.02(2015), Article ID:15173,6
pages
10.12677/AAM.2015.42011
Controllability of Linear Discrete-Time Systems with Time-Delay in State
Juanjuan Zhang, Caixia Gao
School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia
Email: zhangjuanjuan2009512@126.com, gaocx0471@163.com
Received: Apr. 15th, 2015; accepted: Apr. 29th, 2015; published: May 5th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, a data-based method is used to analyze the controllability of linear discrete-time systems with time-delay in state. By this method, one can directly construct a controllability matrix using the measured state data without identifying system parameters. Hence, one can save time in practice and avoid corresponding identification errors. Moreover, it is feasible to the study of characteristics of deterministic systems.
Keywords:Controllability, Time-Delay in State, Linear Discrete-Time System, Data-Based Method
状态时滞的离散线性系统的能控性分析
张娟娟,高彩霞
内蒙古大学数学科学学院,内蒙古 呼和浩特
Email: zhangjuanjuan2009512@126.com, gaocx0471@163.com
收稿日期:2015年4月15日;录用日期:2015年4月29日;发布日期:2015年5月5日

摘 要
本文使用一种基于数据的方法来分析状态时滞的离散线性系统的能控性,利用这种方法,不需要识别系统的参数,就可以通过测量数据,构造一个能控矩阵来分析系统的能控性。因此在实践中,就可以节省时间并且避免相应的识别错误,对确定系统特性的研究也是可行的。
关键词 :能控性,状态时滞,离散线性系统,基于数据的方法

1. 引言
线性系统的能控性概念是卡尔曼在1960年首次提出来的。当系统用状态空间描述以后,能控性便成为线性系统的一个重要结构特性。在现代控制理论中,研究系统稳定性、状态反馈设计、最优控制等方面,能控性都起到了重要作用。所谓系统的能控性是指在一个无约束的控制之下,系统能够从任意初始状态转移到任意终端状态的性质。众多学者对线性系统和非线性系统的能控性问题进行了大量的研究[1] -[4] 。
时滞现象不仅出现在物理和生物系统中,而且在实际的工程应用中也受到了特别关注。因为在工程应用中处理时滞系统的问题比通常系统的更加困难,所以研究时滞现象已成为当今控制领域的一个重要课题。虽然近年来对于正线性无时滞离散系统的能控性已经有了大量的研究 [5] - [8] ,但是关于离散时滞线性系统能控性的研究却少之又少 [9] [10] 。在 [11] 中提出了能控性实现指数 ,这个概念使得离散时滞线性系统的能控性得以更好的解决。关于该系统的能控性研究受到了越来越多人的青睐。
,这个概念使得离散时滞线性系统的能控性得以更好的解决。关于该系统的能控性研究受到了越来越多人的青睐。
然而,在许多工程问题中,系统动力模型是未知的,这就导致了系统能控性建模的许多数学条件不容易实现,为了分析系统性能,就必须首先做系统的辨识。虽然有很多方法可以建立系统的动力模型,例如最小二乘法、神经网络方法和支持向量机方法,但通过以上方法来建立系统模型不仅需要花费大量的时间,而且不可避免的会出现识别错误,这就会影响到整体的计算精度。通过前面对系统能控性的分析启发, [12] 提出了一种基于数据的方法来分析离散线性系统的能控性,这样做的好处是不需要建立系统的动力模型就可以完成分析,而且能避免传统建模过程中由于识别错误引起的计算精度下降的问题。
本文其余部分安排如下:首先介绍了一些基本定义与初步结果;其次利用基于数据的方法来分析状态时滞的离散线性系统的能控性;最后给出一个数值算例并总结。
2. 预备知识与主要引理
给定状态时滞的离散时滞线性系统的状态方程如下:
 (1)
(1)
其中 为状态向量,
为状态向量, 为输入向量,
为输入向量,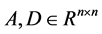 ,
, 为实常数矩阵,正整数
为实常数矩阵,正整数 是状态时滞的步长,这里给定任意的初始状态
是状态时滞的步长,这里给定任意的初始状态 。本文所讨论的能控性是指无约束的能控性或者说是完全能控性。下面给出能控性的定义:
。本文所讨论的能控性是指无约束的能控性或者说是完全能控性。下面给出能控性的定义:
定义1. 系统(1)是(完全)能控的,如果对于任意的初始状态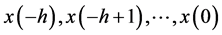 和任意的终端状态
和任意的终端状态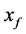 ,存在一个正整数
,存在一个正整数 和输入
和输入 使得
使得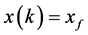 。
。
定义2. 对于系统(1),如果存在一个正整数 ,对于任意的初始状态
,对于任意的初始状态 和任意的终端状态
和任意的终端状态 ,存在一个输入
,存在一个输入 ,满足
,满足 ,那就称
,那就称 为系统(1)的
为系统(1)的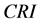 。显然,若这样的
。显然,若这样的 一存在的话,则
一存在的话,则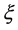 不是唯一的。记最小的
不是唯一的。记最小的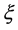 为
为 。
。
引理1. [12] 给定离散线性系统的状态方程如下:
 (2)
(2)
这里 ,
, 。则系统(2)是能控的,当且仅当
。则系统(2)是能控的,当且仅当 。其中
。其中 是
是 的维数,
的维数, 是系统(2)的能控矩阵。
是系统(2)的能控矩阵。
引理2. [11] 系统(1)的通解由如下方程给出:
 (3)
(3)
其中 是零输入时的解,
是零输入时的解, 。
。
引理3. [11] 系统(1)是能控的,当且仅当 。
。
引理4. [11] 对于系统(1),存在 满足
满足
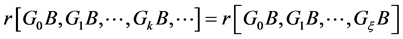
令 ,则
,则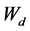 是系统(1)的能控矩阵。
是系统(1)的能控矩阵。
注1:从引理4可知, 是系统(1)的一个
是系统(1)的一个 ,系统(1)能控性可以通过
,系统(1)能控性可以通过 个步骤实现。所以离散时滞线性系统的
个步骤实现。所以离散时滞线性系统的 是存在的,它的值也是有限的,而且
是存在的,它的值也是有限的,而且 的值取决于
的值取决于 ,
, 和
和 。
。
引理5. [11] 对于系统(1),若 ,则
,则 是系统(1)的一个
是系统(1)的一个 。
。
3. 状态时滞的离散线性系统的能控性分析
引理 6. [12] 在系统(2)上做 组数据测试,对于所有的
组数据测试,对于所有的 组测试,让它们都有相同的初始状态
组测试,让它们都有相同的初始状态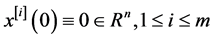 ,以及相应的输入控制
,以及相应的输入控制
 (4)
(4)
这里 的第
的第 个元素是1,其余元素均为0。在所有的
个元素是1,其余元素均为0。在所有的 组测试中,状态轨迹都从原点出发,每个测试组都选用(4)式中的输入向量,
组测试中,状态轨迹都从原点出发,每个测试组都选用(4)式中的输入向量, 是
是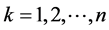 时的状态测量数据,定义
时的状态测量数据,定义
 (5)
(5)
则系统(2)是完全能控的,当且仅当 。
。
定理 7. 在系统(1)上做 组数据测试,对于所有的
组数据测试,对于所有的 组测试,让其状态轨迹从相同的初始状态
组测试,让其状态轨迹从相同的初始状态

出发,并且选定任意的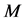 个向量
个向量 。
。
令 ,且
,且 。对于第
。对于第 组测试,相应的输入为
组测试,相应的输入为
 (6)
(6)
在 时测量
时测量 ,定义:
,定义:
 (7)
(7)
则系统(1)是能控的,当且仅当(7)中的矩阵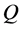 满足
满足 。
。
证明:对于第 组测试,初始状态
组测试,初始状态 ,即满足(3)式中的
,即满足(3)式中的 ,任意的控制输入
,任意的控制输入 ,状态测量为:
,状态测量为:
 (8)
(8)
由于 ,
, 和
和 是未知的,故
是未知的,故 也是未知的,由
也是未知的,由 的定义可以得到:
的定义可以得到:
 (9)
(9)
由于 ,由(9)式可以得到:
,由(9)式可以得到:
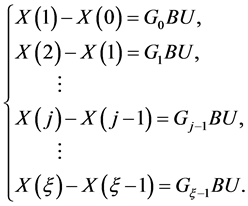
因为 ,由(7)式可知,
,由(7)式可知,

故 ,由引理3和引理4可知,系统(1)是能控的,证毕。
,由引理3和引理4可知,系统(1)是能控的,证毕。
注2:在系统上做数据测试的次数是由输入向量 的维数来确定的。在本文中,控制输入向量
的维数来确定的。在本文中,控制输入向量 ,则只需在系统上做m组数据测试。
,则只需在系统上做m组数据测试。
注3:若系统(1)的时滞为0,则系统(1)可写成
 (10)
(10)
令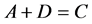 ,则方程(10)可写成
,则方程(10)可写成
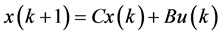 (11)
(11)
这时方程(11)的通解为:
 (12)
(12)
由引理1可得到(11)的能控性矩阵
 (13)
(13)
由此可得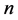 是系统(11)的
是系统(11)的 (满足
(满足 )。当且仅当
)。当且仅当 ,系统(11)是能控的。这个能控性准则就是 [12] 中所提到的。
,系统(11)是能控的。这个能控性准则就是 [12] 中所提到的。
4. 算例
在本节中,将使用一个数值例子来说明基于数据的方法的优点。
考虑方程(1),当 ,
,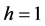 的情况,即
的情况,即
 (14)
(14)
其中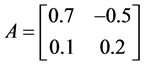 ,
,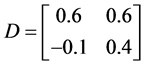 ,
, 。
。
在鉴别矩阵 、
、 和
和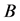 过程中产生的识别误差分别用
过程中产生的识别误差分别用 、
、 和
和 表示;
表示;

下面用两种方法分析方程(14)的能控性。
由引理5可知,系统的能控性实现指数 。
。
1) 传统方法
能控性矩阵为

其中 ,
, ,
, ,
,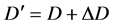 。
。
通过计算,则
 (15)
(15)
对于(15)式,如果把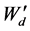 中的元素四舍五入的到小数点后一位,那么上式中的第2,3,4,5列将全部为零。其结果是
中的元素四舍五入的到小数点后一位,那么上式中的第2,3,4,5列将全部为零。其结果是 ,系统就不能控了,计算出来的结果就是不真实的。
,系统就不能控了,计算出来的结果就是不真实的。
2) 基于数据方法
基于数据为基础的方法不需要识别参数矩阵 、
、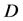 和
和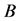 ;因此相应的识别误差
;因此相应的识别误差 和
和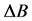 也不会在最后的结果中出现。
也不会在最后的结果中出现。
能控性矩阵为 ,其中
,其中 。
。
通过计算,则

 ,而且如果把上面矩阵的元素四舍五入到小数点后一位,则上面矩阵变为
,而且如果把上面矩阵的元素四舍五入到小数点后一位,则上面矩阵变为
 (16)
(16)
这时 满秩。因此可以得出结论,方程(16)中定义的系统是能控的,这与实际情况相一致。
满秩。因此可以得出结论,方程(16)中定义的系统是能控的,这与实际情况相一致。
5. 总结
本文研究使用的数据为基础的方法,该方法只使用测量数据直接构造矩阵分析状态时滞的离散线性系统的能控性。该方法不需要确定参数矩阵,并且能够避免相应的识别误差。然而仍然有许多工作要做。对于状态与输入都时滞的离散线性系统、离散时变线性系统以及切换系统的时滞能控性,都有待进一步研究。
致谢
作者衷心感谢导师高彩霞副教授的悉心指导和热心鼓励,感谢中国自然科学基金(基金编号: 11261033)的资助。向给予转载和引用权的资料,文献,研究思想和设想的所有者,表示感谢。感谢审稿人的审稿意见。
基金项目
中国自然科学基金(基金编号:11261033)。
文章引用
张娟娟,高彩霞, (2015) 状态时滞的离散线性系统的能控性分析
Controllability of Linear Discrete-Time Systems with Time-Delay in State. 应用数学进展,02,83-89. doi: 10.12677/AAM.2015.42011
参考文献 (References)
- 1. Klamka, J. (1977) Absolute controllability of linear systems with time-variable delays in control. International Journal of Control, 26, 57-63.
- 2. Jakubczyk, B. and Sontag, E. (1990) Controllability of nonlinear discrete-time systems: A lie-algebraic approach. SIAM Journal on Control and Optimization, 28, 1-33.
- 3. Zhao, S. and Sun, J. (2009) Con-trollability and observability for a class of time-varying impulsive systems. Nonlinear Analysis: Real World Applications, 10, 1370-1380.
- 4. Liu, Y. and Zhao, S. (2011) Controllability for a class of linear time-varying impulsive systems with time delay in control input. IEEE Transactions on Automatic Control, 56, 395-399.
- 5. Murthy, D. (1986) Controllability of a linear positive dynamic system. International Journal of Systems Science, 17, 49-54.
- 6. Rumchev, V. and James, D. (1989) Controllability of positive linear discrete-time systems. International Journal of Control, 50, 845-857.
- 7. Fanti, M., Maione, B. and Turchiano, B. (1990) Controllability of multi-input positive discrete-time systems. International Journal of Control, 51, 1295-1308.
- 8. Valcher, M. (1996) Controllability and reachability criteria for discrete time positive systems. International Journal of Control, 65, 511-536.
- 9. Phat, V. (1989) Controllability of discrete-time systems with multiple delays on controls and states. International Journal of Control, 49, 1645-1654.
- 10. Liu, Y. and Fong, I. (2012) On the controllability and observability of discrete-time linear time-delay systems. International Journal of Systems Science, 43, 610-621.
- 11. Yang, P., Xie, G. and Wang, L. (1999) Controllability of linear discrete-time systems with time-delay in state. http://dean.pku.edu.cn/bksky/1999tzlwj/5.pdf
- 12. Wang, Z. and Liu, D. (2011) Data-based controllability and obser-vability analysis of linear discrete-time systems. IEEE Transactions on Neural Networks, 22, 2388-2392.