Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19531,10
pages
10.12677/AAM.2017.61002
Research on the Blasting Solution of a Class of Semilinear Parabolic Equations
Liang Zhang1, Jianjun Li2
1College of Science, Inner Mongolia University of Technology, Hohhot Inner Mongolia
2College of Science, Liaoning Technical University, Fuxin Liaoning

Received: Dec. 20th, 2016; accepted: Jan. 9th, 2017; published: Jan. 16th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This article uses the variable index function to research the local solution of a class of semilinear parabolic equations of the blasting quality. In the limited domain of homogeneous Dirichlet condition, variable index function is the non-negative and bounded. With boundary condition of exponential function, we can define the local solution of semilinear parabolic equation at the condition of big initial data and arbitrary initial data of blasting conditions. Finally, we summarize all blasting properties about equations, and it was proved that the equation satisfies a Fujita type of conclusion; namely equation solution can be blasting in the variable index function and the size of domain that conditions of the nontrivial initial data are determinated.
Keywords:Semilinear Parabolic Equations, Variable Index Function, The Conclusion of the Fujita

一类半线性抛物方程的解的爆破性质研究
张亮1,李建军2
1内蒙古工业大学理学院,内蒙古 呼和浩特
2辽宁工程技术大学理学院,辽宁 阜新

收稿日期:2016年12月20日;录用日期:2017年1月9日;发布日期:2017年1月16日

摘 要
本文通过变量指数函数来研究一类半线性抛物方程的局部解的爆破性质。在齐次狄利克雷条件的有限域中,变量指数函数认为是非负有界的。通过指数函数的边界条件,可以确定半线性抛物方程局部解在大初始数据条件和任意初始数据条件下爆破的条件。最后,对方程所有爆破性质进行总结,证明所分析的方程满足一个Fujita类型的结论,即方程的解可以在变量指数函数和域的大小这些条件确定的任意非平凡初始数据中产生爆破。
关键词 :半线性抛物方程,变量指数函数,Fujita类型的结论

1. 引言
早在1966年,在文献 [1] 中,Fujita, H.就已经对简单的半线性抛物方程 进行解的性质分析,并研究它的爆破解。此后,对于半线性抛物方程解的爆破性质研究吸引着大量的学者,在1986年,文献 [2] 中,Aguirre, J.,Escobedo, M.在前一个方程的基础理论之上,继续研究
进行解的性质分析,并研究它的爆破解。此后,对于半线性抛物方程解的爆破性质研究吸引着大量的学者,在1986年,文献 [2] 中,Aguirre, J.,Escobedo, M.在前一个方程的基础理论之上,继续研究 ,作者采用正则化,比较原理等方法进一步分析爆破解的性质。文献 [3] 中,Escobedo, M.,Herrero, M.A.对半线性抛物方程的有界性及爆破解的性质进行了研究。文献 [4] 中,Escobedo, M.,Herrero, M.A.对半线性抛物方程的指数进行了分类,研究其方程爆破解的性质。文献 [5] 中,Ferreira, R.,de Pablo, A.,Pérez-Llanos, M.,Rossi, J.D.讨论了半线性抛物方程的指数变量。文献 [2] [3] [4] [5] 对于基础模型的半线性抛物方程的研究极为透彻,是本文创作的理论基石。文献 [6] [7] 为本文的证明提供了有效的方程性质。
,作者采用正则化,比较原理等方法进一步分析爆破解的性质。文献 [3] 中,Escobedo, M.,Herrero, M.A.对半线性抛物方程的有界性及爆破解的性质进行了研究。文献 [4] 中,Escobedo, M.,Herrero, M.A.对半线性抛物方程的指数进行了分类,研究其方程爆破解的性质。文献 [5] 中,Ferreira, R.,de Pablo, A.,Pérez-Llanos, M.,Rossi, J.D.讨论了半线性抛物方程的指数变量。文献 [2] [3] [4] [5] 对于基础模型的半线性抛物方程的研究极为透彻,是本文创作的理论基石。文献 [6] [7] 为本文的证明提供了有效的方程性质。
国内对于半线性抛物方程的爆破解的研究成果有很多,但绝大多数并没有建立一套分析半线性抛物方程的手段。近几年来,关于半线性抛物方程爆破解的研究论文层出不穷。在文献 [8] 中,陆求赐,江秋香进行了关于带时滞的退化半线性抛物方程组解的爆破解研究。在文献 [9] 中,凌征球,覃思乾关于非线性非局部边界条件的半线性耦合抛物型方程组的爆破解进行了研究。文献 [10] 中,旷雨阳,王东就一类半线性抛物方程弱解的爆破性进行研究。文献 [11] 则给出了在猝灭时刻解对时间导数的爆破性。文献 [12] 中,刘洋,达朝究,李富明关于Nehari流形在一类半线性抛物方程爆破中的应用进行了一系列研究。本文通过对抛物方程的指数函数类型的讨论,来研究方程的解是否具有爆破性质,这一方法可以说为抛物方程解的性质分析开辟了先河。
2. 方程介绍
在本文中,考虑该半线性抛物方程组:
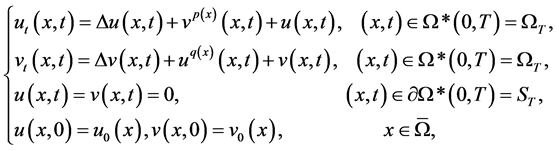 (1.1)
(1.1)
 是
是 上的一个有界光滑域,
上的一个有界光滑域, ,
, (且不恒等于0),
(且不恒等于0), ,此外:
,此外:
 (1.2)
(1.2)
当 有一个为常量时,(1.2)式一定成立。引入下列表示:
有一个为常量时,(1.2)式一定成立。引入下列表示:
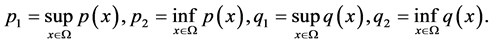
本文的目的是:证明变量指数函数 满足的条件,使得所研究的半线性抛物方程的解具有爆破性。进一步证明该方程满足一个Fujita类型的结论,即方程的解可以在变量指数函数和域的大小这些条件确定的任意非平凡初始数据中产生爆破。
满足的条件,使得所研究的半线性抛物方程的解具有爆破性。进一步证明该方程满足一个Fujita类型的结论,即方程的解可以在变量指数函数和域的大小这些条件确定的任意非平凡初始数据中产生爆破。
3. 方程与解的处理
本节介绍方程解的正则化处理与(1.1)式的相关比较原则。首先考虑正则化问题:
引理2.1 存在 ,使得正则化问题:
,使得正则化问题:
 (2.1)
(2.1)
存在唯一非负解 。
。
证明:应用一般性的方法 [2] [3] 。构造:
 (2.2)
(2.2)
 和
和 是关于
是关于 在
在 满足利普希兹连续。
满足利普希兹连续。
 (2.3)
(2.3)
(2.1),(2.2),(2.3)一直遵循:

通过比较原则得到: 。因此:
。因此:

(2.2)中的 和
和 满足利普希兹条件,(2.3)的非负解具有存在性和唯一性 [6] 。
满足利普希兹条件,(2.3)的非负解具有存在性和唯一性 [6] 。
我们根据(2.3)中解 的比较原则,假设
的比较原则,假设 是(2.1)的一个非负下解,即:
是(2.1)的一个非负下解,即:
 (2.4)
(2.4)
当 ,定义
,定义
若 ,我们得到
,我们得到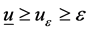 ,因此:
,因此:


当 ,
,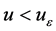 ,则
,则 。
。
综上,可以得到: ,则:
,则:
 (2.5)
(2.5)
同样得到: ,则:
,则:
 (2.6)
(2.6)
根据(2.1),(2.4)到(2.6)可以得到:
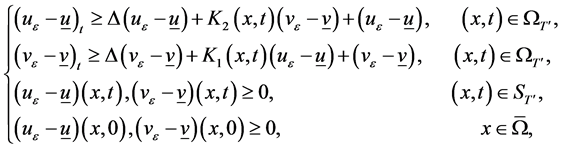 (2.7)
(2.7)
因此,通过比较原则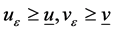 适用于
适用于 [7] ,并且比较原则同样适用于
[7] ,并且比较原则同样适用于
 。
。
考虑(1.1)式局部最大解的存在性。
定理2.1对于某些 ,问题(1-1)在
,问题(1-1)在 中具有非负最大解,可表示为
中具有非负最大解,可表示为 。此外,若
。此外,若 为(1.1)的下解,
为(1.1)的下解, 为(1.1)的上解,且
为(1.1)的上解,且 ,
, 则在
则在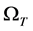 上,
上, 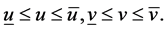
证明: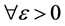 ,让
,让 成为正则化问题(2.1)的唯一解。引理2.1的比较原则暗指解
成为正则化问题(2.1)的唯一解。引理2.1的比较原则暗指解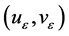 具有单调性。当
具有单调性。当 ,
, 的极限表示为
的极限表示为 。则
。则 就是(1.1)的解。 [3]
就是(1.1)的解。 [3]
在引理2.1中,正则化的比较原则表示上述 是(1.1)的最大解。对于(1.1)的下解
是(1.1)的最大解。对于(1.1)的下解 ,通过引理2.1的比较原则可以得到:当
,通过引理2.1的比较原则可以得到:当 ,
, ,因此:
,因此: 。此外,因为
。此外,因为 ,
, ,所以
,所以 ,当
,当 满足引理2.1使得
满足引理2.1使得 。因此
。因此 。
。
在后文中,(1.1)的解总是表示(1.1)的最大解。
4. 大初始数据的爆破
定理3.1 若 ,则(1.1)式存在一个爆破解。
,则(1.1)式存在一个爆破解。
引理3.1 [4] 对于任意非负可积的函数 ,可以得到:
,可以得到:

引理3.2 [5] 设 是在
是在 上的一个正测度,且
上的一个正测度,且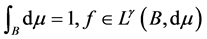 ,并且
,并且 若
若 ,则对某些
,则对某些 ,有
,有

证明:由于 ,我们认为存在一个球域
,我们认为存在一个球域 ,分为两种情况:
,分为两种情况:
(i) 对于
对于 ,
,
(ii) 对于
对于 。
。
当 时,两种情况显然成立。否则,
时,两种情况显然成立。否则, ,使得(3.2)中
,使得(3.2)中
因此, ,在
,在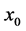 的邻域中,
的邻域中, 或者
或者 。引入下列表示:
。引入下列表示:

我们将证明两种情况下的结论 [4] [7] 。
情况一:当 ,设:
,设:
 (3.1)
(3.1)
 为第一特征值,
为第一特征值,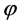 为相应的本征函数。在
为相应的本征函数。在 中,归一化后,
中,归一化后,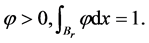 令:
令:

利用Jensen不等式:

类似的:
因此, 满足:
满足:

当 时,
时, 解趋于无穷大,即存在爆破解。
解趋于无穷大,即存在爆破解。
情况二:当 或
或 ,设
,设 足够大,则:
足够大,则:
 (3.2)
(3.2)
在 中,
中, 是椭圆问题
是椭圆问题 的唯一解。我们可以得到:
的唯一解。我们可以得到:

通过引理3.1,我们推断:

因此:
 (3.3)
(3.3)
引用了Fubini的理论,(3.3)等式两侧同乘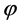 ,令
,令 ,我们得到:
,我们得到:

考虑常微分方程问题:
 (3.4)
(3.4)
令 ,(3.4)式的唯一解表示为:
,(3.4)式的唯一解表示为:
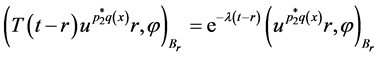
也可以表示为:

通过(3.2)式的引理3.2,我们可以得到:

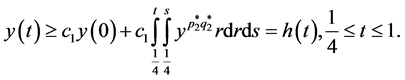
我们令 ,得到:
,得到:
 (3.5)
(3.5)
(3.5)等式两侧同乘 ,然后两侧同时从
,然后两侧同时从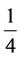 到1进行积分。我们可以得到:
到1进行积分。我们可以得到:
 (3.6)
(3.6)
另一方面:


因为 ,我们得到:
,我们得到:
由于 ,若
,若 (3.6)中在区间
(3.6)中在区间 上
上 。因此,当
。因此,当 ,
, 足够大时,
足够大时, 会产生爆破。
会产生爆破。
5. 任意初始数据的爆破
本节讨论(1.1)的Fujita类型结论 [4] 。
引理4.1 假设 ,并且
,并且 或者
或者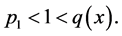 则对于任意
则对于任意 ,并且
,并且 ,存在一个与
,存在一个与 无关的正常数
无关的正常数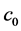 ,有
,有

证明 [4] :只考虑 的情况,另一种
的情况,另一种 的情况可以同样处理。假设
的情况可以同样处理。假设 ,根据比较原则,用
,根据比较原则,用 表示狄利克雷热内核,得到:
表示狄利克雷热内核,得到:
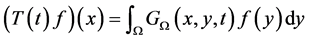 其中
其中
因为 ,我们通过比较原则
,我们通过比较原则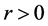 得到:
得到:

因此:
 (4.1)
(4.1)
进而:
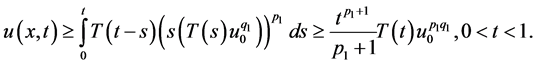
因此,通过用于证明文献 [4] 中引理2.3的方法,我们可以得到:

其中 并且
并且 ,则:
,则: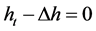 在
在 上,
上, 在
在 上,
上, 在
在 上。
上。
令: ,
,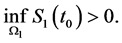 则
则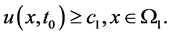
同样的: 设
设 证明完毕。
证明完毕。
推论4.1 在引理4.1的假设下,对于任意的 ,存在
,存在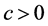 使得:
使得:

证明:令 ,并且
,并且 则可以得到
则可以得到 通过引理4.1,我们可以得到:
通过引理4.1,我们可以得到:

因此,存在 使得:
使得:

其中: ,
, 当用
当用 替换
替换 ,
, 为(3-1)的解。
为(3-1)的解。
通过简单计算,我们可以知道当 足够小时,解
足够小时,解 是下面方程的一个下解:
是下面方程的一个下解:
 (4.2)
(4.2)
该推论得到的结论为:
引理4.2假设在球域:
 满足引理4.1的假定,则存在
满足引理4.1的假定,则存在 使得(1.1)式的解满足:
使得(1.1)式的解满足: ,其中
,其中 并且
并且 ,
,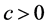 与
与 无关,其中
无关,其中

证明:假设 。构造:
。构造:
我们得到:

同样的, 。因此
。因此 是下面方程的一个上解:
是下面方程的一个上解:
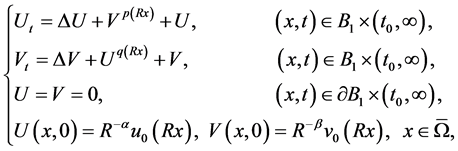 (4.3)
(4.3)
此外,应注意 满足引理4.1的假定,并且推论4.1的
满足引理4.1的假定,并且推论4.1的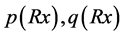 也满足。得到:
也满足。得到:

对于一些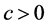 并且独立于
并且独立于 。结论是:
。结论是:
定理4.1假设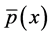 和
和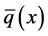 是定义在单位球
是定义在单位球 上函数,
上函数, 在这个单位球变号。如果
在这个单位球变号。如果 足够大,使得当
足够大,使得当 足够大时,
足够大时, 。对于任一简单的非负初始数据,当
。对于任一简单的非负初始数据,当 时,
时, ,(1.1)式的解在有限时间内是爆破的。
,(1.1)式的解在有限时间内是爆破的。
证明 [5] :假设 。当
。当 和
和 足够大时,会出现一个球域
足够大时,会出现一个球域 ,对于任意
,对于任意 ,满足
,满足 和
和 (或者
(或者 );会出现一个球域
);会出现一个球域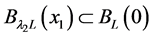 ,对于任意
,对于任意 ,满足
,满足 。这个假设与(1.1)式的解
。这个假设与(1.1)式的解 在
在 下是全局解的结论矛盾。通过引理4.2,对于一些
下是全局解的结论矛盾。通过引理4.2,对于一些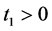 ,并且
,并且 ,我们得到:
,我们得到:

不难检验出解中的 是下面方程的一个上解:
是下面方程的一个上解:
 (4.4)
(4.4)
设 为(4.4)的稳态解。明显地,
为(4.4)的稳态解。明显地,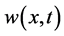 一致收敛于
一致收敛于 ,因此:当
,因此:当 ,而
,而 时,
时, 。在
。在 上,当
上,当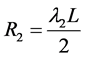 时,
时, 是(3.1)的第一个规范化的特征函数。因为在
是(3.1)的第一个规范化的特征函数。因为在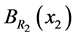 上,
上, 。其中当
。其中当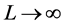 时
时 单调趋于
单调趋于 ,我们知道当
,我们知道当 时,无论
时,无论 是否足够大,
是否足够大, 一定成立。同样
一定成立。同样 的结论同样成立。我们由定理3.1得到(1.1)式的解在
的结论同样成立。我们由定理3.1得到(1.1)式的解在 足够大时,在一定时间内会产生爆破现象。
足够大时,在一定时间内会产生爆破现象。
基金项目
国家自然科学基金资助项目(11661059)。
文章引用
张亮,李建军. 一类半线性抛物方程的解的爆破性质研究
Research on the Blasting Solution of a Class of Semilinear Parabolic Equations[J]. 应用数学进展, 2017, 06(01): 10-19. http://dx.doi.org/10.12677/AAM.2017.61002
参考文献 (References)
- 1. Fujita, H. (1966) On the Blowing up of Solutions of the Cauchy Problem for Fac. Sci., Univ. Tokyo, Sect. I., 13, 109-124.
- 2. Aguirre, J. and Escobedo, M. (1986-1987) A Cauchy problem for with . Asymptotic Beha-viour of Solutions. Ann. Fac. Sci. Toulouse Math., 8, 175-203.
- 3. Escobedo, M. and Herrero, M.A. (1991) Boundedness and Blow up for a Semilinear Reaction Diffusion System. Journal of Differential Equations, 89, 176-202.
- 4. Escobedo, M. and Herrero, M.A. (1993) A Semilinear System in a Bounded Domain. Annali di Matematica Pura ed Applicata, 165, 315-336. https://doi.org/10.1007/BF01765854
- 5. Ferreira, R., de Pablo, A., Pérez-Llanos, M. and Rossi, J.D. (2012) Critical Exponents for a Semilinear Parabolic Equation with Variable Reaction. Proceedings of the Royal Society of Edinburgh, 142A, 1027-1042. https://doi.org/10.1017/S0308210510000399
- 6. Friedman, A. (1964) Partial Differential Equations of Parabolic Type. Prentice Hall, Englewood Cliffs.
- 7. Quittner, P. and Souplet, P. (2007) Superlinear Parabolic Problems. Birkhäuser, Basel.
- 8. 陆求赐, 江秋香. 关于带时滞的退化半线性抛物方程组解的存在性研究[J]. 长江大学学报(自然版), 2014(28): 9-12.
- 9. 凌征球, 覃思乾. 非线性非局部边界条件的半线性耦合抛物型方程组[J]. 数学物理学报, 2015, 35(2): 234-244.
- 10. 旷雨阳, 王东. 一类拟线性抛物方程弱解的存在性及其有界性证明[J]. 科学通报, 2016, 32(1): 31-34.
- 11. 孙仁斌. 半线性抛物方程解在有限时刻猝灭与解整体存在的条件[J]. 中南民族大学学报(自然科学版), 2014(3): 119-122.
- 12. 刘洋, 达朝究, 李富明. Nehari流形在一类半线性抛物方程爆破中的应用[J]. 山东大学学报(理学版), 2016(1): 123-127.