Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20583,6
pages
10.12677/AAM.2017.63027
K-L-Nim Game
Rongxing Xu, Xinzhong Lv, GuiXian Tian
Department of Mathematics Zhejiang Normal University, Jinhua Zhejiang

Received: Apr. 29th, 2017; accepted: May 12th, 2017; published: May 22nd, 2017

ABSTRACT
Perhaps the most famous combinatorial game is Nim, which was completely analyzed by C.L. Bouton in 1902. From then on, the variant of Nim game is getting more and more popular. This paper introduces a new variant of Nim game, K-L-Nim game, one player’s illegal move is to remove k stones from one pile, while the other player’s illegal move is to remove l stones from one pile. This paper gives a complete solution for the game by using Sprague-Grundy Theorem, Bouton Theorem and mathematical induction.
Keywords:Nim Game, Sprague-Grundy Theorem, Bouton Theorem, P-position
K-L-Nim博弈
徐荣兴,吕新忠,田贵贤
浙江师范大学数理与信息工程学院,浙江 金华
收稿日期:2017年4月25日;录用日期:2017年5月12日;发布日期:2017年5月22日

摘 要
Nim博弈是博弈论中最经典的模型之一,1902年C.L. Bouton给出其完全解。其变形版本的玩法日益受到人们的喜爱,这篇文章介绍了一个Nim博弈的变形玩法,K-L-Nim博弈。其中一个玩家每次不能拿走k个石子(但可拿走多于或者少于k个石子),而另外一个玩家不能拿走l个石子(但可拿走多于或者少于l个石子)。这篇文章巧妙地借助了Sprague-Grundy定理研究了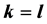 时的组合解。并用数学归纳法和Bouton定理给出了
时的组合解。并用数学归纳法和Bouton定理给出了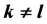 时所有组合解。
时所有组合解。
关键词 :Nim博弈,Sprague-Grundy定理,Bouton定理,P态

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Nim博弈是博弈论中最经典的模型,它有着十分简单的规则和无比优美的结论。它的规则如下:
有若干堆石子,每堆石子的数量都是有限的,两人交替拿走石子,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他此刻没有任何合法的移动)。
1902年,Bouton [1] 给出了这个游戏的所有组合解。从此以后,通过修改Nim博弈的规则,各种各样的Nim类型的博弈就产生了,更多的可以参考 [2] [3] [4] [5] [6] [7] - [12] 。首先我们先来回忆一些组合游戏里的定义。
定义1 假设双方都采取最明智的策略,则对于一些状态,刚刚做完决策的游戏者有一定胜利的策略的状态(Previous Player wins the game)叫做P态。下一个做出决策的游戏者有一定获胜的策略的状态(Next Player wins the game)叫N态。
在有限的公平组合游戏中,P态和N态有如下的性质:
1) 所有终止状态都是P态;
2) 能一步到达P态的状态为N态;
3) 每一步都将到达N态的状态为P态。
要证明一个状态是N态,只需要证明它在一个合法的移动内可以变成一个N态,而要证明一个状态是P态,则需要证明它的任意一个下一步状态都是N态,所以寻找一个Nim类型组合游戏的P态就显得尤为重要。
定义2 两个非负整数的Nim和是指将这两个数换算成二进制以后的不进位相加所得到的值。更详细地,
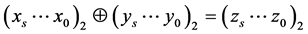 ,
,
其中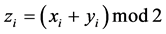 ,也即当
,也即当 为偶数时,
为偶数时,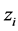 等于0,
等于0,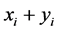 为奇数时,
为奇数时,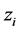 等于1。
等于1。
例3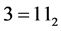 ,
, ,
, 。所以
。所以
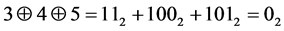 .
.
符号 在本文中,我们假设初始状态有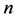 堆石子,每堆数目分别是
堆石子,每堆数目分别是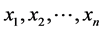 (数目可以重复,为了方便我们假设其为非降序排列)。我们用
(数目可以重复,为了方便我们假设其为非降序排列)。我们用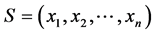 表示其初始状态。另外为了表述方便,我们用P1表示先手,P2表示后手。
表示其初始状态。另外为了表述方便,我们用P1表示先手,P2表示后手。
下面这个定理对普通的Nim博弈的所有的P态进行了一个刻画,那显然其所有对立面的状态就是N态。
Bouton定理 [1] 对于一个在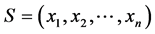 状态上进行的Nim博弈,它是P态当且仅当
状态上进行的Nim博弈,它是P态当且仅当
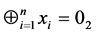 .
.
在这篇文章中,我们考虑一种新的游戏,K-L-Nim博弈,其规则如下。
有若干堆石子,每堆石子的数量都是有限的,两人交替移走石子,合法的移动是“选择一堆石子并拿走若干颗,不能不拿”,但是先手P1每次不能拿走k个石子(但可拿走多于或者少于k个石子),后手P2不能拿走l个石子(但可拿走多于或者少于l个石子),如果轮到某个人时所有的石子堆都已经被拿空了,则判负。
在第二部分,我们介绍当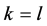 时该博弈的解;在第三部分,我们介绍当
时该博弈的解;在第三部分,我们介绍当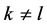 时的解。
时的解。
2. K等于L
在介绍我们的主要结论之前,我们先给出一些定义,以便我们能方便的证明我们的结论。
定义4 用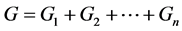 表示由单堆上进行的
表示由单堆上进行的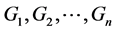 的Nim博弈组成的组合博弈。其中每个玩家可以在每一次走步中选择其中一个子游戏上进行。
的Nim博弈组成的组合博弈。其中每个玩家可以在每一次走步中选择其中一个子游戏上进行。
定义5 对于任意一个仅含一堆的Nim博弈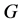 来讲,其Sprague-Grundy函数
来讲,其Sprague-Grundy函数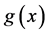 定义如下:对于其终止状态
定义如下:对于其终止状态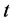 ,
,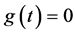 ,对于其他状态,
,对于其他状态,
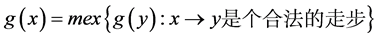 ,
,
其中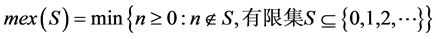 表示局外最小序数。
表示局外最小序数。
Sprague-Grundy定理 [10] 假设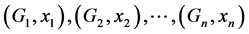 是
是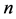 个单堆的Nim博弈及其初始状态。
个单堆的Nim博弈及其初始状态。 ,那么对于博弈
,那么对于博弈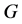 而言,其Sprague-Grundy函数
而言,其Sprague-Grundy函数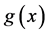 满足
满足
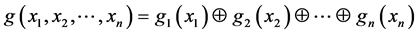 .
.
其中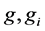 分别表示
分别表示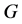 和
和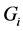 的Sprague-Grundy函数,其中
的Sprague-Grundy函数,其中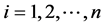 。
。
所以一旦知道一个博弈的Sprague-Grundy函数,我们就很容易的去分析与其相关的博弈。满足使得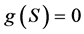 的状态
的状态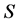 为P态,否则,为N态。
为P态,否则,为N态。
现在我们来考虑K-L-Nim博弈,其中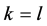 。
。
定理6 假设K-L-Nim博弈在石子数为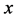 的单堆上进行,其中
的单堆上进行,其中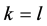 。那么我们有
。那么我们有
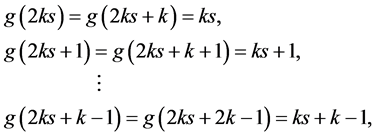
其中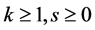 。
。
证明:我们主要对石子的总数采用数学归纳法。
假设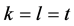 ,所以对两个玩家来说,他们的合法移动是每次拿走
,所以对两个玩家来说,他们的合法移动是每次拿走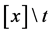 个石子。表1是
个石子。表1是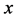 较小的时候的一些Sprague-Grundy函数值。
较小的时候的一些Sprague-Grundy函数值。
也即,
Table 1. The Sprague-Grundy function values of some small xs
表1. x较小的时候的一些Sprague-Grundy函数值
 ,其中
,其中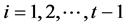 ;
;
 ,其中
,其中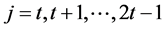 。
。
对于更一般的情形,我们有
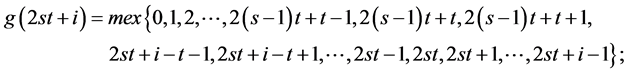
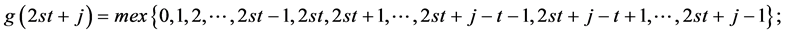
其中 ;
;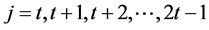 。
。
根据归纳假设,我们知道
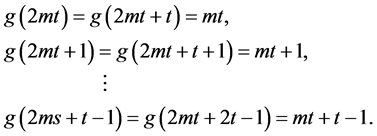
其中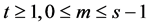 。
。
所以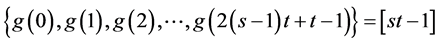 。
。
由于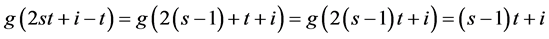 ,所以我们得到
,所以我们得到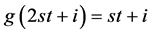 ,其中
,其中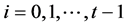 。同理,我们可以得到
。同理,我们可以得到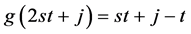 ,其中
,其中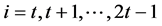 。由
。由 的选择的任意性我们完成了该定理的证明。□
的选择的任意性我们完成了该定理的证明。□
推论7:假设K-L-Nim博弈在石子数为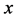 的单堆上进行,且
的单堆上进行,且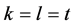 。那么Sprague-Grundy函数值如下
。那么Sprague-Grundy函数值如下
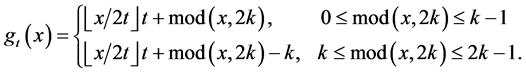
其中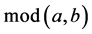 表示
表示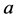 除以
除以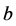 后的余数。
后的余数。
所以对于任意一个在状态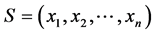 上进行的K-L-Nim博弈(
上进行的K-L-Nim博弈( ),我们可以将其看成是
),我们可以将其看成是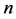 个单堆的Nim博弈的结合,并分别算出这
个单堆的Nim博弈的结合,并分别算出这 个初始状态的Sprague-Grundy函数值。如果这
个初始状态的Sprague-Grundy函数值。如果这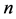 个值的nim和为0,则其初始状态为P态,否则为N态。
个值的nim和为0,则其初始状态为P态,否则为N态。
例8假设K-L-Nim博弈在初始态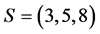 上进行,并且
上进行,并且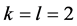 。所以
。所以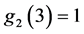 ,
,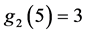 ,
,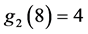 ,
, ,因此这是一个N态。
,因此这是一个N态。
3. K与L不相等
我们假设 。否则这个游戏就变成了普通的Nim博弈。
。否则这个游戏就变成了普通的Nim博弈。
定义9 如果一个状态在普通的Nim博弈中是N态,而它在K-L-Nim博弈的规则下不能在下一步转化成普通Nim博弈里的P态,那么我们说该状态是K-L-Nim博弈里的有缺陷的N态。
例10 假设K-L-Nim博弈在一个初始状态为 的状态上进行,其中
的状态上进行,其中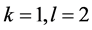 。显然
。显然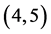 对于K-L-Nim博弈中的P1来说就是一个有缺陷的N态,因为
对于K-L-Nim博弈中的P1来说就是一个有缺陷的N态,因为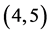 如果想变成普通Nim博弈里的一个P态,需要P1在第一步中从石子数为5的堆里拿走一颗石子,然而很显然,P1并不能做到。
如果想变成普通Nim博弈里的一个P态,需要P1在第一步中从石子数为5的堆里拿走一颗石子,然而很显然,P1并不能做到。
接下来,我们先看一下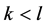 的情形。
的情形。
引理11 对于K-L-Nim博弈,其中 ,如果P2在一个有缺陷的N态上进行,那么他也有一个合法的移动,去留下一个有缺陷的N态给P1。
,如果P2在一个有缺陷的N态上进行,那么他也有一个合法的移动,去留下一个有缺陷的N态给P1。
证明:假设P2面对的状态为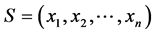 ,由于它是有缺陷的N态,故有
,由于它是有缺陷的N态,故有
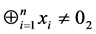 ,
,
并且存在一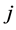 和
和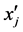 满足,
满足,
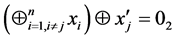 ,
,
其中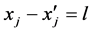 ,否则与缺陷的N态的定义相矛盾。这时P2可以从
,否则与缺陷的N态的定义相矛盾。这时P2可以从 中拿走
中拿走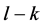 个石子,此时剩余状态为
个石子,此时剩余状态为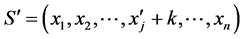 ,显然这对P1来说是一个有缺陷的N态。□
,显然这对P1来说是一个有缺陷的N态。□
定理12 对于K-L-Nim博弈,其中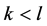 ,如果P1面对一个有缺陷的N态或者普通Nim博弈中是P态的状态,那么P2有必胜的策略。
,如果P1面对一个有缺陷的N态或者普通Nim博弈中是P态的状态,那么P2有必胜的策略。
证明:我们对石子的总数采用数学归纳法。无论P1面对一个有缺陷的N态还是普通Nim意义下的P态,在P1移动完以后,剩余的状态一定是普通状态里的N态,所以根据引理11以及Bouton定理,P2一定有策略使得他做完移动后剩余一个P态或者有缺陷的N态,由归纳假设可知,P2有必胜的策略。□
引理13 对于K-L-Nim博弈,其中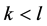 ,如果P2面对一个P态
,如果P2面对一个P态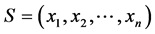 。只要
。只要 ,那么P2就有一个策略去留下一个带缺陷的N态给P1。
,那么P2就有一个策略去留下一个带缺陷的N态给P1。
证明:由于 是一个普通Nim博弈里的P态,所以有
是一个普通Nim博弈里的P态,所以有
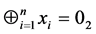 ,
,
不失一般性,我们假设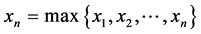 。P2的策略是从
。P2的策略是从 中拿走
中拿走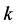 个石子。留下状态
个石子。留下状态 给P1,不难证明这个状态对于P1来讲是一个有缺陷的N态,因为P1若是想将状态
给P1,不难证明这个状态对于P1来讲是一个有缺陷的N态,因为P1若是想将状态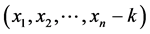 转化成普通Nim博弈里的P态,他必须在某一堆里拿走
转化成普通Nim博弈里的P态,他必须在某一堆里拿走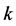 个石子,显然这是对于P1来讲是个不合法的移动。□
个石子,显然这是对于P1来讲是个不合法的移动。□
定理14 对于K-L-Nim博弈,其中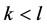 ,如果在P1走完第一步以后,剩余状态是在普通的Nim博弈里的一个P态,并且
,如果在P1走完第一步以后,剩余状态是在普通的Nim博弈里的一个P态,并且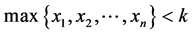 ,那么P1有必胜的策略,否则P2有必胜的策略。
,那么P1有必胜的策略,否则P2有必胜的策略。
证明:如果P1留下一个普通的Nim博弈里的一个P态给P2,并且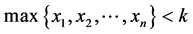 ,那么无论P2做出怎样的决策,既不能留下一个有缺陷的N态,也不能留下一个普通Nim博弈意义下的P态给P1,所以此时P1有必胜的策略。
,那么无论P2做出怎样的决策,既不能留下一个有缺陷的N态,也不能留下一个普通Nim博弈意义下的P态给P1,所以此时P1有必胜的策略。
定理的后半部分皆可由引理11,定理12以及引理13证明出来,在此不再赘述。□
参照上述几个引理及定理的P2的策略,不难得到下面这个推论。
推论15 对于K-L-Nim博弈,其中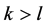 ,P1总有必胜的策略。
,P1总有必胜的策略。
至此,我们给出了该博弈在所有状态下的N态和P态。
致谢
感谢浙江师范大学“千人计划”朱绪鼎教授给本文的很多指导性的意见,也感谢审稿人给出了很多宝贵的修改意见。
基金项目
国家自然科学基金项目资助(KYZKJY11186)。
文章引用
徐荣兴,吕新忠,田贵贤. K-L-Nim博弈
K-L-Nim Game[J]. 应用数学进展, 2017, 06(03): 232-237. http://dx.doi.org/10.12677/AAM.2017.63027
参考文献 (References)
- 1. Bouton, C.L. (1902) Nim, a Game with a Complete Mathematical Theory. Annals of Mathematics, 3, 35-39. https://doi.org/10.2307/1967631
- 2. Albert, M.H. and Nowakowski, R.J. (2001) The Game of End-Nim. The Electronic Journal of Combinatorics, 8, Research Paper 1, 12p.
- 3. Albert, M.H. and Nowakowski, R.J. (2004) Nim Restrictions, Integers. Electronic Journal of Combinatorial Number Theory, 4, #G 01.
- 4. Fukuyama, M. (2003) A Nim Game Played on Graphs. Theoretical Computer Science, 304, 387-399. https://doi.org/10.1016/S0304-3975(03)00292-5
- 5. Li, S.-Y.R. (1978) N-Person Nim and N-person Moore's Games. International Journal of Game Theory, 7, 31-36. https://doi.org/10.1007/BF01763118
- 6. Lim, C.-W. (2005) Partial Nim, INTEGERS: Electronic Journal of Combinatorial Number Theory, 5, # G 02.
- 7. Moore, E.H. (1910) A Generalization of a Game Called Nim. Annals of Mathematics, 11, 93-94. https://doi.org/10.2307/1967321
- 8. Schwartz, B.L. (1971) Some Extensions of Nim. Mathematics Magazine, 44, 252-257. https://doi.org/10.2307/2688631
- 9. Schwenk, A.J. (1970) Take-Away Games. Fibonacci Quarterly, 8, 225-234.
- 10. Sprague, R.P. (1936) Uber Mathematische Kampfspiele. Tohoku Mathematical Journal, 41, 438-444.
- 11. Wythoff, W.A. (1907) A Modification of the Game of Nim. Nieuw Archief voor Wiskunde, 7, 199-202
- 12. Xu, R. and Zhu, X. (2016) Bounded Greedy Nim Game. Theoretical Computer Science, Submitted
