Advances in Applied Mathematics
Vol.06 No.06(2017), Article ID:22108,6
pages
10.12677/AAM.2017.66088
Generalized for a Class of Resource Allocation Strategy Model
Yaqiang Wang1, Yaotang Li2
1Institute of Mathematics and Information Science, Baoji University of Arts and Sciences, Baoji Shaanxi
2School of Mathematics and Statistics, Yunnan University, Kunming Yunnan

Received: Aug. 26th, 2017; accepted: Sep. 12th, 2017; published: Sep. 19th, 2017

ABSTRACT
Based on the classic resource allocation model, a general resource allocation strategy model is presented which includes reproductive allocation, survival allocation and sex allocation. From the analyzing the generalized model, we find that: 1) when the adult survivorship, the fitness of female and the juvenile survivorship are linear function of their respective resource investment, and the fitness of male is power function of its respective resource investment, reproductive allocation is independent on sex allocation; 2) when reproductive allocation is greater than 0 and smaller than 0.5, survival allocation increases as reproductive allocation increases; when reproductive allocation is greater than 0.5 and smaller than 1, survival allocation increases as reproductive allocation decreases; in particular, when reproductive is equal to 0.5, survival allocation is independent on reproductive allocation. These results provide a reasonable explanation for the phenomenon of “more reproducing but less caring” and “less reproducing but more caring” in the plant kingdom.
Keywords:Reproductive Allocation, Sex Distribution, Survival Distribution, Evolutionary Stable Strategies, Fitness
一类资源分配策略模型的推广
王亚强1,李耀堂2
1宝鸡文理学院,数学与信息科学学院,陕西 宝鸡
2云南大学,数学与统计学院,云南 昆明
收稿日期:2017年8月26日;录用日期:2017年9月12日;发布日期:2017年9月19日

摘 要
在经典资源分配策略模型的基础上,建立了包含繁殖分配、存活分配和性别分配的更具一般性的资源分配策略模型。通过对所建模型分析发现:1) 当成年存活率,雌性适合度和后代存活率是资源投入的线性函数,且雄性适合度是资源投入的幂函数时,繁殖分配与性别分配互不影响;2) 当繁殖分配大于0且小于0.5时,生存分配随着繁殖分配增大而增大;当繁殖分配大于0.5且小于1时,生存分配随着繁殖分配增大而减小;特别地,当繁殖分配等于0.5时,生存分配不随繁殖分配的变化而变化。本文结果为植物中的“多生劣养”或“少生优养”的现象提供一个合理的理论解释。
关键词 :繁殖分配,性别分配,存活分配,进化稳定策略,适合度

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在植物整个生长发育阶段,可利用的资源是有限的,不但存活、生长和繁殖等各种功能竞争有限的资源,而且在雌雄两性功能之间也存在着资源的竞争。由于这种竞争使得植物必在各功能之间进行一个权衡(trade-off),以使自己的适合度达到最大,即存在资源分配策略的选择问题 [1] [2] [3] [4] 。植物生活史性状之间基本权衡包括:1) 繁殖与存活之间的权衡,即植物将多少比例的资源用于繁殖,而将剩余的资源用于存活(自身存活与后代存活)。将可利用资源中用于繁殖的资源比例称为繁殖分配(reproductive allocation),通常用 来表示,那么用于存活的资源比例就为 ;2) 雄性(male function)和雌性(female function)功能之间的权衡,即植物将繁殖资源的多少用于生产雄性和多少用于生产雌性之间的权衡,将用于繁殖的资源中生产雄性的资源比例称为性别分配(sex allocation) [2] [3] [4] ;3) 自身存活与后代存活之间的权衡,即将存活资源的多少用于自身生存,其余用于后代生存,将用于存活的资源中分配给后代生存的比例称为存活分配(survival allocation)。关于资源分配策略的研究一直都是植物生活史进化研究的热点问题之一 [5] - [13] 。
1994年,张大勇和王刚注意到了繁殖分配和性别分配是共用一个有限资源的,因此他们将繁殖分配和性分配纳入到同一个理论框架进行研究 [2] [6] 。通过这种整合研究揭示出了繁殖分配与性别分配独立研究所需的前提条件。然而,他们的模型忽略另一个在植物繁殖中发挥重要作用的资源分配——存活分配,存活分配是指植物将用于存活的资源中一部分资源用来维持后代存活。同时,张大勇和王刚的模型及其推广模型将后代存活率看成一个常数,这也与实际情况不符 [14] 。事实上,后代存活率在很大程度上是依赖于用于后代存活的资源比例,即存活分配。因此,将繁殖分配、存活分配和性别分配纳入到同一个框架研究是必要的。然而,在已有的文献中,笔者还没有见到将繁殖分配、存活分配和性别分配整合在同一个框架下的文献。
本文通过建立包含繁殖分配、存活分配和性别分配的进化稳定的资源分配模型,揭示这三类分配之间的相互关系,以及它们独立研究的所需的前提条件。
2. 包含繁殖分配、存活分配和性别分配的进化稳定的资源分配模型
2.1. 经典的资源分配模型回顾
1994年,张大勇和王刚在文 [6] 中提出了如下资源分配模型:
, (1)
其中 , 分别表示 时刻纯合子 的成年个体数量与杂合子 的数量; , 分别表示纯合子 个体和杂合子个体 将总资源中用于繁殖的比例; , 分别表示纯合子 个体和杂合子个体 将繁殖资源中用于生产的花粉(雄性)的资源比例; 表示生产的种子数量, 表示生产的花粉数量, 表示成年个体从 到 时刻的存活率,且 , 和 为其投入资源的函数; 表示后代存活率,且为常数 [2] [6] 。
在上述模型的基础上,下面我们将在植物生长繁殖过程中发挥重要作用的资源分配——存活分配引入模型,建立更具一般性的资源分配模型。
2.2. 模型的基本假设
考虑一个雌雄同株的、常年生的植物种群。假设年龄是离散的,个体之间的交配是随机的,世代重叠。与1994年张大勇和王刚的资源分配模型一样,进一步假设年龄对成年存活率,受精率没有影响 [6] 。假设每个成年个体拥有的可利用资源为 ,并将这些资源分配给四方面功能:花粉生产、种子生产、自身生存以及后代生存(详见图1)。
假设种群是由纯合型( )个体组成。令 表示将可利用资源分配给存活的资源比例,即繁殖分配;令 表示将用于繁殖的资源分配给雄性功能(生产花粉)的资源比例,即性别分配;令 表示将用于存活的资源分配给后代的资源比例,即存活分配;从而, 表示用于繁殖的资源分配给雌性功能(种子生产)的资源比例;因此,在我们的模型中有三个变量,即繁殖分配 、性别分配 和存活分配 。由于成年个体存活率 ,种子数量 ,花粉数量 和后代存活率 都是各自资源投入的函数,故可记
, , 与 .
根据上述资源分配模式及假设,可建立如下含有存活分配的更具一般性的资源分配模型,其中纯合子个体 种群的动态方程为:
,
它的增长率是:
. (2)
记杂合型 个体的资源分配模式为 ,则杂合子 种群的动态方为:
(3)
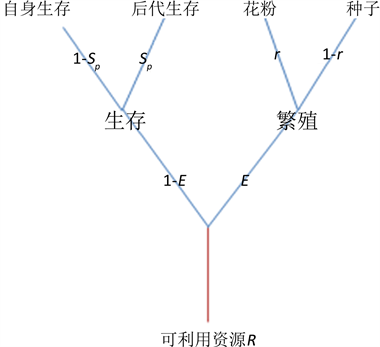
Figure 1. Schematic of resource allocation
图1. 植物资源分配示意图
其中 表示由杂合子 生产的种子存活到成年体的数量。由于生产这些种子的雄性肯定会是 型,这些存活下来的种子的一半将会是 型。此外, 表示 型熟花粉粒占总的花粉池的比例。 表示以 型个体为父亲的种子存活到成年体的数量,同理,这些存活下来的种子的一半将会是 型。因此杂合子 个体的增长率可表示为:
.(4)
由方程(4)易知, 不仅依赖于自身的资源分配策略 ,而且也受到纯合子个体资源分配策略 的影响。
由于资源分配策略 是占大多数的纯合子个体采取的分配策略,由进化稳定策略的定义知 [2] [13] ,资源分配策略 是进化稳定策略。因此,由进化稳定理论知 [13] ,对于采用 资源分配策略的个体来说,必有 ,即 在 处取得极大值。因此,由极大值的必要条件得:
(5)
(6)
(7)
3. 进化稳定的资源分配策略
与经典的资源分配模型一致 [6] ,进一步假设 , 和 是资源投入的线性函数,而 是资源投入的幂函数,即
, (8)
, (9)
, (10)
, (11)
其中 表示投入单位比例的资源可提高的成年存活率; 表示投入单位比例资源可生产的种子数量; 表示投入单位比例资源可提高的后代存活率; 表示投入单位比例资源可生产的花粉数量,因此有 , 和 , 。
把(8)~(11)代入(5)~(7),并令 ,解得进化稳定的资源分配策略为:
(12)
4. 结果与讨论
首先,由(12)式知,当 , 和 是资源投入的线性函数,且 是资源投入的幂函数时, 且 。这表明此时进化稳定的繁殖分配E不依赖于性别分配 ,且进化稳定的性别分配也不依赖于繁殖分配。事实上,1982年Charnov在其专著The Theory of Sex Allocation中就讨论了该问题,指出:如果种子生产不受花粉短缺的制约,那么雌性适合度函数 将是一个资源投入的线性函数,即 。同时,采用幂函数来描述雄性适合度与资源投入的关系,即 。然而,Charnov只考虑了雄性和雌性功能之间的权衡 [4] [6] 。1994年,张大勇和王刚在文 [6] 中对该问题进行了进一步研究,同时考率了繁殖分配和性别分配,并且得到当雌性适合度函数 是一个资源投入的线性函数且雄性适合度是资源投入的幂函数时,繁殖分配与性别分配互不影响 [6] [12] 。本文的结果与张大勇和王刚1994年得到的结果是一致,但他们结果是在 是常数的条件下得到的,这里 更具一般性 [6] 。
其次,由(12)式知,当 , 和 是资源投入的线性函数,且 是资源投入的幂函数时, 。于是由函数 的性质知,当 时,生存分配 随着繁殖分配E增大而增大;而当
时,生存分配随着繁殖分配增大而减小;特别地当 时,生存分配不随繁殖分配的变化而变化。在植物繁殖过程经常会出现少生优养和多生劣养的现象,在苹果、梨等一些主要果树上这类现象表现得更为明显 [15] 。事实上,当果树结果多时,即分配给用于繁殖的资源较多(模型中 的情况)时,消耗的养分多,枝条内养分贫乏,即用于幼果存活的资源就变少,从而导致许多幼果不能发育而脱落,出现结果较多而果存活率较低的现象,即“多生劣养”的现象。而当果树结果较少时,即分配给用于繁殖的资源较少(模型中 的情况)时,枝条内养分充分,从而出现结果较少而存活较高的现象,即“少生优养”的现象。本文的这个结果表明:许多植物可以根据外部环境来调整不同繁殖分配策略,使得繁殖分配或大或小,进而导致“多生劣养”或“少生优养”的现象。这也很好地解释了为什么有些植物会出现结果的大小年现象。
基金项目
国家自然科学基金(31600299),陕西省教育厅基(17JK0040),宝鸡文理学院重点项目(ZK16050)。
文章引用
王亚强,李耀堂. 一类资源分配策略模型的推广
Generalized for a Class of Resource Allocation Strategy Model[J]. 应用数学进展, 2017, 06(06): 734-739. http://dx.doi.org/10.12677/AAM.2017.66088
参考文献 (References)
- 1. 赵志刚, 杜国祯, 刘左军. 雌雄同花植物的性分配[J]. 生态学报, 2005, 25(10): 2725-2733.
- 2. 张大勇. 理论生态学研究[M]. 北京: 高等教育出版社, 2000: 66-78.
- 3. 赵志刚, 杜国祯, 任青吉. 5种毛茛科植物个体大小依赖的繁殖分配和性分配[J]. 植物生态学报, 2004, 28(1): 9- 16.
- 4. Charnov, E.L. (1982) The Theory of Sex Allocation. Monographs in Population Biology, 18, 121-129.
- 5. Bell, G. (1980) The Costs of Reproduction and Their Consequences. The American Naturalist, 116, 45-76. https://doi.org/10.1086/283611
- 6. Zhang, D.Y. and Wang, G. (1994) Evolutionarily Stable Reproductive Strategies in Sexual Organisms: An Integrated Approach to Life-History Evolution and Sex Allocation. American Naturalist, 144, 65-75. https://doi.org/10.1086/285661
- 7. 苏晓磊, 曾波, 乔普, 阿依巧丽, 黄文军. 冬季水淹对秋华柳的开花物候及繁殖分配的影响[J]. 生态学报, 2010, 30(10): 2585-2592.
- 8. 侯勤正, 叶广继, 马小兵, 苏雪, 张世虎, 孙坤. 青藏高原不同生境下湿生扁蕾(Gentianopsis paludosa)个体大小依赖的繁殖分配[J]. 生态学报, 2016, 36(9): 2686-2694.
- 9. Wenk, E.H. and Falster, D.S. (2015) Quantifying and Understanding Reproductive Allocation Schedules in Plants. Ecology & Evolution, 5, 5521-5538. https://doi.org/10.1002/ece3.1802
- 10. Baldanzi, S., Mcquaid, C.D. and Porri, F. (2015) Temperature Effects on Reproductive Allocation in the Sandhopper Talorchestia capensis. Biological Bulletin, 228, 181-191. https://doi.org/10.1086/BBLv228n3p181
- 11. Brzyski, J.R., Taylor, W. and Mcletchie, D.N. (2014) Reproductive Allocation between the Sexes, across Natural and Novel Habitats, and Its Impact on Genetic Diversity. Evolutionary Ecology, 28, 247-261. https://doi.org/10.1007/s10682-013-9672-9
- 12. West, S.A. (2010) Sex Allocation. Princeton: Princeton University Press, 257-273. https://doi.org/10.1038/srep33976
- 13. Wang, Y.Q., Li, Y.T. and Wang, R.W. (2016) The Evolution of Optimal Re-source Allocation and Mating Systems in Hermaphroditic Perennial Plants. Scientific Reports, 6, 33976.
- 14. Fudenberg, D. and Tirole, J. (1991) Game Theory. Mit Press Books, 841-846.
- 15. 书睿. 果树的大小年现象[J]. 西北园艺: 果树专刊, 2013(3): 50-51.