ABSTRACT

A strong edge coloring of graph G is on the basis of the proper edge coloring and requiring any two edges at distance at most 2 receive distinct colors, the smallest integer of strong edge coloring called a figure of colors used strong edge chromatic number of G. In this paper, the configuration of the minimal counter example is given, and then the power transfer method is used to prove that the strong edge chromatic number of the plane graph is at most $3\Delta \left(G\right)+1$ if G has no k-cycle ( $5\le k\le 10$ ) and the 3-cycle and 4-cycle are non-intersect each other.

Keywords:Planar Graphs, Strong Edge Coloring, Strong Edge Chromatic Number, Cycle

不含短圈平面图的强边染色

张恒

浙江师范大学数理与信息工程学院，浙江 金华

收稿日期：2018年5月22日；录用日期：2018年6月7日；发布日期：2018年6月14日

摘 要

图G的强边染色是在正常边染色的基础上，要求距离不超过2的任意两条边染不同的颜色。强边染色所用颜色的最小整数称为图G的强边色数。文章首先给出极小反例的构型，然后通过权转移方法，证明了3-圈、4-圈互不相交且没有k-圈( $5\le k\le 10$ )的平面图的强边色数至多是 $3\Delta \left(G\right)+1$ 。

关键词 :平面图，强边染色，强边色数，圈

Copyright © 2018 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文考虑的图都是简单无向图。对于一个平面图G，把它顶点集、边集、面集、最大度分别记为 $V\left(G\right)$ ， $E\left(G\right)$ ， $F\left(G\right)$ 和 $\Delta \left(G\right)$ ，用 $d\left(v\right)$ 、 $d\left(f\right)$ 分别表示顶点、面的度，如果顶点v的度等于k (至少是k或至多是k)，则称v是k-点(k⁺-点或k⁻-点)。1-点又称悬挂点，k_l-点是指与l个2-点相邻的k-点，顶点v的一个k-邻点指的是 $N\left(v\right)$ 中度为k的顶点。k-圈指的是长为k的圈，如果两个圈至少有一个公共顶点(或一条公共边)，则称它们是相交(或相邻的)。好3-面指的是不关联2-点的3-面，坏3-面指的是关联一个2-点的3-面。好4-面指的是不关联2-点的4-面，弱4-面是关联一个2-点的4-面，把一个关联两个不相邻2-点的4-面称为坏4-面。 $N_2\left(uv\right)$ 表示与边uv的距离不超过2的边构成的集合，给定图G的一个边染色c，记 $SC\left(N_2\left(uv\right)\right)=c\left(e\right)|e\in N_2\left(uv\right)$ 。

图G的强边染色(也称为2-距离边染色)，是指对图G的边进行正常染色，使得长为3的路上的任意两条边染不同的颜色。强边染色所用颜色的最小整数称为图G的强边色数，记为 ${{\chi }^{\prime }}_s\left(G\right)$ 。1985年Erdős [1] 等提出了强边染色猜想：

猜想1 (Erdős, Nešet ř il)。设图G的最大度为Δ，则

1) 若Δ为偶数，则 ${{\chi }^{\prime }}_s\left(G\right)\le \frac{5}{4}{\Delta }^2$ ；

2) 若Δ为奇数，则 ${{\chi }^{\prime }}_s\left(G\right)\le \frac{1}{4}\left(5{\Delta }^2-2\Delta +1\right)$ 。

当时，猜想显然成立。Andersen [2] 和Horák [3] 证明了当 $\Delta \le 3$ 时猜想成立。当 $\Delta =4$ 时，Cranston [4] 等证明了 ${{\chi }^{\prime }}_s\left(G\right)\le 22$ 。Molloy和Reed [5] 证明了当Δ充分大时，强边染色的上界不超过 $1.998{\Delta }^2$ 。对于平面图强边染色的研究，始于Faudree [6] 等用四色定理和Vizing’(s)定理证明了平面图的强边色数 ${{\chi }^{\prime }}_s\left(G\right)\le 4\Delta +4$ 。当围长足够大时，文献 [7] [8] 证明了平面图的强边色数可以达到下界 $2\Delta -1$ 。2014年，Hudák [9] 等证明了 $g\left(G\right)\ge 6$ 的平面图G有 ${{\chi }^{\prime }}_s\left(G\right)\le 3\Delta +5$ ，后来Bensmail [10] 等把该结果改进为当平面图 $g\left(G\right)\ge 6$ 时， ${{\chi }^{\prime }}_s\left(G\right)\le 3\Delta +1$ ；当 $g\left(G\right)\ge 4$ 且 $\Delta \ge 5$ 时， ${{\chi }^{\prime }}_s\left(G\right)\le 4\Delta$ 。孟献青在文献 [11] 证明了没有k-圈( $4\le k\le 10$ )且3-圈不相交的平面图有 ${{\chi }^{\prime }}_s\left(G\right)\le 3\Delta +1$ ，本文推广了该结果，证明了没有k-圈( $5\le k\le 10$ )且3-圈、4-圈互不相交的平面图其强边色数 ${{\chi }^{\prime }}_s\left(G\right)\le 3\Delta +1$ 。

2. 定理及其证明

定理1设最大度为 $\Delta \left(G\right)$ 的平面图G不包含k-圈( $5\le k\le 10$ )且3-圈、4-圈互不相交，则G的强边色数 ${{\chi }^{\prime }}_s\left(G\right)\le 3\Delta +1$ 。

证明：当 $\Delta \left(G\right)\le 3$ 时，由文献 [2] [3] ，定理成立。下面只需证明 $\Delta \left(G\right)\ge 4$ 的情形。假设定理1结论不成立，则存在一个不包含k-圈( $5\le k\le 10$ )且3-圈、4-圈互不相交，但 ${{\chi }^{\prime }}_s\left(G\right)>3\Delta +1$ ，使 $\left|V\left(G\right)\right|+\left|E\left(G\right)\right|$ 最小的平面图，由极小性知，G为连通平面图，而对G的任何一个真子图 $G^{\prime }$ 是 $\left(3\Delta \left(G^{\prime }\right)+1\right)$ -强边可染的，同时G还具有以下性质。

2.1. 极小反例的性质

引理1 [10] 设v是图G的一个顶点且 $d\left(v\right)=k$ 。

1) 若 $k=1$ ，则1-点的邻点是5⁺-点；

2) 若 $k=2$ ，则2-点的两个邻点不能同时是两个3^--点，或一个3⁻-点和一个4₃-点，或一个3⁻-点和一个4₃-点，或一个4₂-点和一个4₃-点；

3) 若 $k\ge 4$ ，则v至多与 $k-1$ 个2⁻-点相邻；

4) 若 $k\ge 5$ ，则v至多与 $k-3$ 个1-点相邻；若v恰好与 $k-3$ 个1-点相邻。则v不与其他的2⁻-点相邻；

5) 若 $k\ge 5$ ，且v相邻 $\alpha$ 个1-点和 $k-2-\alpha$ 个2-点，则 $0\le \alpha \le k-4$ ，且至多有 $k-4-\alpha$ 个2-点的邻点是3⁻-点或4₃-点；

6) 若 $k\ge 5$ ，且v相邻 $k-1$ 个2⁻-点，则这 $k-1$ 个2⁻-点都是2-点，且这些2-点的另一个邻点是不同于4₃-点的4⁺-点。

引理2 [11] 若2-点v与3-圈关联，则v的另两个邻点是5⁺-点。

引理3 [11] 设G有一个3-圈 $uvwu$ ，满足 $d\left(u\right)=2$ ， $d\left(w\right)\ge 5$ ， $d\left(v\right)=k\ge 5$ ，则

1) v至多与 $k-2$ 个2⁻-点相邻；

2) 若v与 $k-4$ 个1-点相邻，则v至多只有一个2-邻点；

3) 若v与 $\alpha$ 个1-点和 $k-2-\alpha$ 个2-点相邻，则 $0\le \alpha \le k-5$ ，且至多有 $k-5-\alpha$ 个2-点的邻点是3⁻-点或4₃-点。

引理4 [12] 4-面不能关联两个相邻的2-点。

引理5 [12] 设v与弱4-面f关联，且f边界上的顶点按顺时针方向记为u，w，z，v，满足 $d\left(u\right)=2$ ， $d\left(w\right)\ge 5$ ， $d\left(v\right)=k\ge 5$ 。若v与 $\alpha$ 个1-点和 $\beta$ 个2-点相邻，则

1) $\alpha \le k-4$ ，且若 $\alpha =k-4$ ，则 $\beta =1$ 。

2) 若 $\alpha +\beta =k-2$ ，则 $0\le \alpha \le k-5$ ，且至多有 $\beta -2$ 个2-点的邻点是3⁻-点或4₃-点。

引理6 [12] 设v与坏4-面f关联，且f边界上的顶点按顺时针方向记为u，w，z，v，满足 $d\left(u\right)=d\left(z\right)=2$ ， $d\left(w\right)\ge 3$ ， $d\left(v\right)=k\ge 5$ 。若v与 $\alpha$ 个1-点和 $\beta$ 个2-点相邻，则

1)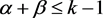，且 $\alpha \le k-5$ ；若 $\alpha =k-5$ ，则 $\beta =2$ 。

2) 若 $k\ge 6$ ， $\alpha +\beta =k-2$ ，则 $0\le \alpha \le k-6$ ，且至多有 $\beta -2$ 个2-点的邻点是3⁻-点或4₃-点。

2.2. 权转移规则

对连通平面图G，由欧拉公式，有 $\left|V\left(G\right)\right|-\left|E\left(G\right)\right|+\left|F\left(G\right)\right|=2$ 及 ${\displaystyle \underset{v\in V\left(G\right)}{\sum }d\left(v\right)}={\displaystyle \underset{f\in F\left(G\right)}{\sum }d\left(f\right)}=2\left|E\left(G\right)\right|$ ，

可得：

${\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(2d\left(v\right)-6\right)}+{\displaystyle \underset{f\in F\left(G\right)}{\sum }\left(d\left(f\right)-6\right)}=-12$

对每一个 $x\in V\left(G\right)\cup F\left(G\right)$ ，定义其初始权值为 $ch\left(x\right)$ 。对任意 $v\in V\left(G\right)$ ，定义 $ch\left(v\right)=2d\left(v\right)-6$ ，而对于 $f\in F\left(G\right)$ ， $ch\left(f\right)=d\left(f\right)-6$ ，则 ${\displaystyle \underset{x\in V\left(G\right)\cup F\left(G\right)}{\sum }ch\left(x\right)}=-12<0$ 。下面定义权转移规则，重新分配顶点和面的权，使得对每个 $x\in V\left(G\right)\cup F\left(G\right)$ ，都有 $c{h}^{\prime }\left(x\right)\ge 0$ 。由于只在顶点和面之间进行权转移，故权总和不变，从而 $0\le {\displaystyle \underset{x\in V\left(G\right)\cup F\left(G\right)}{\sum }c{h}^{\prime }\left(x\right)}={\displaystyle \underset{x\in V\left(G\right)\cup F\left(G\right)}{\sum }ch\left(x\right)}=-12<0$ ，矛盾。说明极小反例不存在，从而定理成立。

权转移规则如下：

R1 设v为1-点，则

R1.1 每个与v相关联的面f给v转2；

R1.2 每个与v相邻的5⁺-点给v转2；

R2 设v为2-点， $N\left(v\right)=u,w$ ，且 $d\left(u\right)\le d\left(w\right)$ ，则

R2.1 若u是3⁻-点，则w给v转2；

R2.2 若u是4₃-点，则u给v转 $\frac{2}{3}$ ，w给v转 $\frac{3}{4}$ ；

R2.3 否则，u和w分别给v转1。

R3 若f为3-面，则

R3.1 每个与f相邻的面g给f转权1；

R3.2 每个5⁺-点给相关联的坏3-面转 $\frac{1}{2}$ 。

R4 若f是4-面，面g与f有k条公共边，则g给f转权 $\frac{k}{2}$ 。

下面验证新权 $c{h}^{\prime }\left(x\right)\ge 0,x\in V\left(G\right)\cup F\left(G\right)$ ：

由R1.1知，每个面给相关联的1-点转2，而每增加一个悬挂点，面的度增加2，故悬挂点不影响面的转权。所以在验证面的权时，不考虑面f上的悬挂点。

首先检验。

设f为3-面， $ch\left(f\right)=-3$ 。若f是好3-面，由R3.1， $c{h}^{\prime }\left(f\right)=-3+3\times 1=0$ ；若f是坏3-面，由引理2，f关联两个5⁺-点，由R3.2，这两个5⁺-点给f转权 $2\times \frac{1}{2}$ ；再由R3.1，与f相邻的面给f转权 $1\times 2$ ，因此 $c{h}^{\prime }\left(f\right)=-3+2\times 1+2\times \frac{1}{2}=0$ 。

设f为4-面， $ch\left(f\right)=-2$ 。当f为好4-面，由R4， $c{h}^{\prime }\left(f\right)=-2+4\times \frac{1}{2}=0$ 。

设f为k-面( $k\ge 11$ )，则 $ch\left(f\right)=k-6$ 。由于3-圈、4-圈之间互不相交，再由引理4，与4-面关联的2个2-点不相邻，故f至多与 $\lfloor \frac{k}{2}\rfloor$ 个3-面、4-面关联，由R3，R4易知 $c{h}^{\prime }\left(f\right)\ge k-6-\lfloor \frac{k}{2}\rfloor \times 1\ge 0$ 。

下面再验证 $c{h}^{\prime }\left(v\right)\ge 0,\forall v\in V\left(G\right)$ 。

情况1：v为1-点，则 $ch\left(v\right)=-4$ 。由引理1(1)知，1-点的邻点是5⁺-点，故由R1， $c{h}^{\prime }\left(v\right)=-4+2+2=0$ 。

情况2：v为2-点，则 $ch\left(v\right)=-2$ 。由R2， $c{h}^{\prime }\left(v\right)=-2+\min \left\{2,\frac{2}{3}+\frac{4}{3},1+1\right\}=0$

情况3：v为3-点，根据转权规则，3-点权值没有改变，所以 $c{h}^{\prime }\left(v\right)=ch\left(v\right)=0$ 。

情况4：v为4-点，则 $ch\left(v\right)=2$ 。由引理1(1)，引理1(3)，v无1-邻点且至多有3个2-邻点。

若v是4₀-点或4₁-点，由R2， $c{h}^{\prime }\left(v\right)\ge 2-1\times \max \left\{1,2,\frac{3}{4}\right\}=0$ ；

若v是4₂-点，设v的2个2-邻点是x，y，由引理1(2)可知x和y除v点外的邻点是不同于4₃-点的4⁺-点，故由R2.3， $c{h}^{\prime }\left(v\right)\ge 2-2\times 1=0$ ；

若v是4₃-点，设v的3个2-邻点是x，y，z，由引理1(2)可知x，y和z除v点外的邻点是4₁-点或

5⁺-点，故由R2.2， $c{h}^{\prime }\left(v\right)=2-3\times \frac{2}{3}=0$ 。

情况5：v为k-点( $k\ge 5$ )，则 $ch\left(v\right)=2k-6$ 。分两种情况讨论：

1) v不与坏3-面关联。

由引理1(3)，v至多与 $k-1$ 个2^--点相邻。

① 若v恰与 $k-1$ 个2^--点相邻，由引理1(6)，v的 $k-1$ 个2⁻-点都是2-点，且2-点的邻点是不同于4₃-点的4⁺-点，由R2.3， $c{h}^{\prime }\left(f\right)\ge 2k-6-\left(k-1\right)\times 1=k-5\ge 0$ 。

② 若v恰与 $k-2$ 个2⁻-点邻，设有 $\alpha$ 个1-邻点，由引理1(5)，引理5(2)，引理6(2)知，v的 $k-2-\alpha$ 个2-邻点中至多有 $k-4-\alpha$ 个2-点与3⁻-点或4₃-点相邻，即v至少有2个2-邻点除v点外的另一个邻点不是3⁻-点、4₃-点，此时由R1.2，R2.1，R2.3，有 $c{h}^{\prime }\left(f\right)\ge 2k-6-\alpha \times 2-\left(k-4-\alpha \right)\times 2-2\times 1=0$ 。

③ 若v至多与 $k-3$ 个2⁻-点相邻，设有 $\alpha$ 个1-邻点， $\beta$ 个2-邻点，则由引理1(4)，引理5(1)，引理6(1)知，仅当 $\alpha =k-3$ ， $\beta =0$ ；或 $\alpha =k-4$ ， $\beta =1$ ；或， $\beta =2$ 且v的2-邻点除v外的另一个邻点是3⁻-点时，顶点v转出的权最大，由R1.2，R2.1， $c{h}^{\prime }\left(f\right)\ge 2k-6-\left(k-3\right)\times 2=0$ 。

2) v与坏3-面 $vuwv$ 关联 $\left(d\left(u\right)=2\right)$ 。

由引理2，v与w均为5⁺-点。由引理3(1)，v至多与 $k-2$ 个2⁻-点相邻。

① 若v至多与 $k-3$ 个2⁻-点相邻。由R2.3，v给u转权1，再由R1.2，R3.2知

$c{h}^{\prime }\left(v\right)\ge 2k-6-\left(k-4\right)\times 2-1\times 1-\frac{1}{2}=\frac{1}{2}>0$ 。

② 若v恰与 $k-2$ 个2⁻-点相邻，且v有 $\alpha$ 个1-邻点，由引理3(3)， $\alpha \le k-5$ 且v的 $k-2-\alpha$ 个2-邻点中至多有 $k-5-\alpha$ 个2-点与3⁻-点或4₃-点相邻，根据R1.2，

R2，R3.2知， $c{h}^{\prime }\left(f\right)\ge 2k-6-\alpha \times 2-\left(k-5-\alpha \right)\times 2-3\times 1-\frac{1}{2}=\frac{1}{2}>0$ 。

综合以上各种情况，我们验证了对任意的 $x\in V\left(G\right)\cup F\left(G\right)$ ，都有 $c{h}^{\prime }\left(x\right)\ge 0$ ，从而得到如下矛盾的式子：

$0\le {\displaystyle \underset{x\in V\left(G\right)\cup F\left(G\right)}{\sum }c{h}^{\prime }\left(x\right)}={\displaystyle \underset{x\in V\left(G\right)\cup F\left(G\right)}{\sum }ch\left(x\right)}=-12$ .

上面的这个矛盾说明G不存在，从而完成了定理1的证明。

文章引用

张 恒. 不含短圈平面图的强边染色
Strong Edge Coloring of Planar Graphs without Short Cycles[J]. 应用数学进展, 2018, 07(06): 661-666. https://doi.org/10.12677/AAM.2018.76078

参考文献