Advances in Applied Mathematics
Vol.
08
No.
01
(
2019
), Article ID:
28386
,
19
pages
10.12677/AAM.2019.81002
Time-Splitting Compact Difference Scheme for Solving Schrodinger-Poisson Equations
Shan Jiang, Ronghua Liu, Xiu Ma, Hanquan Wang
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Dec. 11th, 2018; accepted: Jan. 2nd, 2019; published: Jan. 9th, 2019

ABSTRACT
In this paper, we have introduced fourth-order compact finite difference, the time splitting method and the Crank-Nicolson method to solve the nonlinear Schrödinger-Poisson equations. Based on fast Sine transform, we construct a fast solver for the fully discretized system. The presented numerical algorithm has been used to solve one-dimensional, two-dimensional and three-dimensional nonlinear Schrödinger-Poisson equations. We provide specific numerical examples. Through the MATLAB software, we write matlab programs based on the presented numerical algorithm, calculate approximated error and draw the approximated numerical solution. The numerical results prove that the presented algorithm has spectral accuracy in space direction. They also confirm its efficiency and stability.
Keywords:Nonlinear Schrodinger-Poisson Equations, High Order Compact Difference Scheme, Sine Transform, Time Splitting Method
求解薛定谔–泊松方程组的时间分裂紧致 差分格式
姜珊,刘荣华,马秀,王汉权
云南财经大学统计与数学学院,云南 昆明

收稿日期:2018年12月11日;录用日期:2019年1月2日;发布日期:2019年1月9日

摘 要
本文通过应用高阶紧致差分格式,时间分裂法与Crank-Nicolson法等方法求解非线性薛定谔–泊松方程组。基于快速Sine变换,我们设计了一种求解离散系统的快速算法。我们用该算法分别求解一维、二维、三维的非线性薛定谔–泊松方程组。我们列举具体的数值例子,使用MATLAB软件编写出算法程序,并且通过程序计算近似误差与画出近似解的图像。数值计算结果证实了该算法在空间方向具有谱精度,也证实了该算法的高效性与稳定性。
关键词 :非线性薛定谔–泊松方程组,四阶紧致差分,Sine变换,时间分裂法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
带电粒子的运动规律通常用耦合的动力学方程(例如弗拉索夫方程或波尔兹曼方程)与泊松方程进行描述 [1] [2] [3] [4] 。在考虑粒子的量子隧道效应情形下,带电粒子的运动规律也可用非线性薛定谔泊松方程组来描述,这主要是因为耦合的动力学-泊松方程组可近似化简为非线性薛定谔泊松方程组 [3] [4] 。非线性薛定谔泊松方程组最早由Hatree得到。他在研究原子物理学中的电子对原子核的库伦势的自洽作用(self-consistenteffect)时,发现带电粒子的运动可由非线性薛定谔泊松方程组 [5] 来描述。后来此方程组被广泛应用到量子等离子体 [3] 、量子输运 [6] 、量子半导体 [7] 、分子链 [8] 等物理现象中。本文主要想通过非线性薛定谔泊松方程组的数值解来模拟相关量子物理现象(例如纳米级带电粒子的运动规律)。
据我们所知,前人提出了多种数值方法来求解非线性薛定谔泊松方程组。为了模拟半导体纳米结构,Chen等人提出了一种新奇的快速谱元法 [9] ,他们在求解该方程组的过程中,未知函数的空间变量由高阶勒让德多项式展开;为了计算球对称的薛定谔泊松方程组的基态和动力学现象,Dong研究了一种简化伪谱方法 [10] ;为研究一种非磁化作用的稠密热等离子的物理现象,Shaikh等人针对薛定谔泊松方程组提出了一种傅里叶谱方法,并进行了三维非线性流体在纳米级尺度下湍流的模拟 [11] ;Mauser等人为薛定谔泊松方程组提出了一个向后欧拉法和半隐式/蛙跳正弦伪谱方法,并用该方法计算相关粒子的基态和动力学 [12] ;Zhang等人为该方程组提出了一种紧致差分格式,并研究了该数值方法的最优误差估计;我们还注意到前人研究了球对称形式的薛定谔泊松方程组的稳态解 [13] 。
关于非线性薛定谔泊松方程组的数学理论研究,前人已经开展了许多工作:Ben Abdallahd等人研究了薛定谔泊松方程组的稳态解与动态解的弱解存在性 [2] ;Brezzi等人基于非线性薛定谔泊松方程组的解证明了量子Vlasov-Poisson方程组的全局经典解的存在性 [14] ;Castella等人研究了薛定谔泊松方程组在L2范数意义下解的存在性、唯一性 [15] ;Lange等人显示了Wigner-Poisson方程组与薛定谔泊松方程组的解在不同边界条件(周期性边界条件、混合边界条件)下的存在性、唯一性与正则性 [6] 。
本文将为非线性薛定谔泊松方程组的求解提出一种时间分裂紧致差分格式,重点讨论如何基于Sine变换实现该方法的快速求解过程,并简单讨论该方法的数值特点。本文的结构安排如下:在第1.1节至第1.3节中,对薛定谔泊松方程组的物理模型做了简单介绍,同时也对紧致差分格式的构造、离散Sine变换做了相关阐述。在第2节中,详细推导了用时间分裂紧致差分格式来求解一维、二维、三维的薛定谔泊松方程组的数值计算过程,重点讨论如何基于Sine变换实现离散系统的快速求解过程。在第3节中,通过几个具体的数值例子的计算结果,证实了在前两节中介绍的方法可实现一维、二维、三维薛定谔泊松方程组方程组的数值计算,并验证了数值方法的守恒性。
1.1. 1.1. 问题背景
多粒子量子系统是由多个粒子通过相互作用形成的微观系统,它广泛存在于半导体物理、等离子物理、凝聚态物理和分子动力学等领域,对它的科学研究具有重要意义。本文研究的薛定谔–泊松方程组是对多粒子非相对论量子系统的一种单粒子波函数近似。薛定谔–泊松方程组是对含时Hartree-Fock方程组的一种单粒子波函数局部近似,它的无量纲形式为 [16] [17] [18] [19] [20] [21] [22]
(1.1)
(1.2)
其中d (=1, 2, 3)为空间维数,β为一已知常数,波函数 是复值函数,且满足无穷远条件
(1.3)
为外势函数,形式已知。ϕ为泊松位势,通常写成卷积形式。
薛定谔–泊松方程组(1.1)~(1.2)本身有许多守恒量,例如:粒子数N(t),粒子冲量P(t),粒子角动量L(t)与粒子总能量E(t)均不随时间变化而变化,其中,
粒子数
(1.4)
粒子冲量
(1.5)
粒子旋转量
(1.6)
与粒子总能量
(1.7)
1.2. 紧致差分格式设计
有限差分法是计算机数值模拟最早采用的方法,至今仍被广泛使用,其主要思想就是在空间和时间两个方向上将问题离散化。传统的差分格式是显式地通过各点函数值的线性组合来表示函数的导函数,而紧致差分格式是隐式地利用网格点的函数值的线性组合来表示导函数的线性组合,需要通过求解方程组来得到每个网格点的导数值。这两种方法相比较,当达到相同精度时,紧致差分格式需要的网格点少,计算精度高。
紧致差分格式的构造最早由 紧致差分格式的构造最早由Lele提出 [23] ,在文 [24] 中也有介绍。在本节中,我们简要地叙述紧致差分格式的构成。通常把未知函数u(x)的定义区间[a, b]作M等分, 称为步长,
称为节点,记 , , , , ,其中i与M是正整数,a与b是给定的区间端点。
紧致差分格式想从下式中隐式地得到函数u(x)在节点xi处的近似值 ( ):
(1.8)
其中α,β,a,b,c是一些待定系数。由泰勒展开式可知由下式得到的近似值 ( )具有四阶精度
(1.9)
上式可称为一种四阶紧致差分格式。
另外由泰勒展开式可知由下式得到的近似值 ( )具有六阶精度
(1.10)
上式可称为一种六阶紧致差分格式。
1.3. 一维的离散Sine变换与逆变换
为了实现高效的数值算法,首先看一维的离散Sine变换:
(1.11)
一维的离散Sine逆变换:
(1.12)
其中,记
通过方程(1.11),我们可写出 , , , , 的Sine变换:
(1.13)
把上述等式带入与四阶紧致差分格式相关的方程(1.9),得
利用三角公式化简为:
根据对应项分别相等, 得
(1.14)
方程(1.14)显示了 与 之间的联系。而式子(1.11)与(1.13)建立了函数u(x)在节点xi处的值与二阶导数 在节点xi处的值之间的联系。
重要的是,上述离散Sine变换(1.11)与离散Sine逆变换(1.12)可借助快速的离散傅里叶变换实现,快速的离散傅里叶变换将离散Sine变换(1.11)与逆变换(1.12)的计算量从 减少至 。
同理,如果把相关等式代入与六阶紧致差分格式相关的方程(1.10),那么也可得与(1.14)类似的等式:
(1.15)
方程(1.15)也显示了 与 之间的联系。
2. 快速高效的数值方法
在本节中,我们先分别介绍如何利用时间分裂紧致差分格式法离散一维非线性薛定谔泊松方程组、二维非线性薛定谔泊松方程组、三维非线性薛定谔泊松方程组,然后介绍如何基于一维的快速Sine变换、二维的快速Sine变换、三维的快速Sine变换来求解上述方法离散后的方程组,最后写出详细的离散求解过程。
2.1. 一维非线性薛定谔泊松方程组的求解方法
考虑如下一维非线性薛定谔泊松方程组初边值问题:
(2.16)
(2.17)
其中 , 。 为常数, 为已知函数, 为未知函数。
先将[a,b]等分成M份,则空间步长为 ,节点为 ;再将[0,T]等分成N份,则时间步长为 ,节点为 ,记 分别为 的
近似值。
通过观察会发现:方程(2.16)类似于非线性薛定谔方程,(2.17)是一个泊松方程。对于(2.16)方程,在一个时间步长 上,我们利用时间分裂法将该方程分两步求解:
先求解非线性部分 。可巧妙地利用共轭与积分性质:等式两边同时乘ψ的共轭 ,得: ,再对它两边同时取共轭,得:
(2.18)
注意到ϕ是一个实值函数,将以上两式相减得: ,也即 。我们可以得到 。再从泊松方程 可知 。因此,非
线性部分方程的求解变为:
(2.19)
(2.20)
(2.21)
记 , 作为时间分裂法的中间变量,但在方程(2.21)中,仍有未知量 。由已知条件 ,即 ,其中记 。可先利用四阶紧致差分格式离散一维泊松方程 ,然后对离散后的方程组做Sine变换得 (详细过程见 [25] )。该式子右边
是由fj做Sine变换得到;同时由基于Sine变换的四阶紧致差分格式,得到关系式:
(2.22)
其中 ,这样就可以通过式子(2.22)求出 。再利用一次Sine变换这样就求出 的值,将其带入到方程(2.21),就可以求出中间变量 。
再考虑线性部分: 的求解。此时以 做为初始条件,对于该方程时间方向上采用
Crank-Nicolson公式离散:
(2.23)
对上述方程,空间上采用四阶紧致差分格式来离散。由于等式右边 已知,对上述离散后的新系统做Sine逆变换得 。再结合关系式:
(2.24)
得 。再做Sine变换就得 。这样方程(2.23)的右边函数值全部已知,记 ,对(2.23)两边同时做Sine变换 ,其中 是 经过一维的Sine逆变换得到的。对方程
(2.23)左边,我们利用基于Sine变换的四阶紧致差分格式的关系式:
(2.25)
得到
(2.26)
这样 可以被求出,利用一次Sine变换,就可求出 。在时间方向上就形成了一次完整的迭代过程。体算法可以总结如下:
1) 输入a,b,T,M,L,β,以及 ;
2) 计算 , , , , 。从 出发;
3) 计算 ,通过Sine逆变换得 ,利用 ,再对 做Sine 变换得 ;
4) 由式子 ,计算出 ( );
5) 通过Sine逆变换求出 ,再利用关系式(2.24),求出 。利用Sine变换求出 ,再从 的Sine逆变换求出 ;
6) 由 得到 ,再对其做一次Sine变换就可得到 。再令 ,重复3~6直到 为止。
2.2. 二维非线性薛定谔泊松方程组的求解方法
考虑二维零边界的非线性薛定谔泊松方程组的初边值问题:
(2.27)
(2.28)
其中 , , , 均为常数, , 均是已 知函数,而 是未知函数。
首先,将区域 等分成M份,步长为 ,节点为 ;将区域 等分成N份,步长为 ,节点为 ;将区域 等分成L份,步长为 ,节点为 ;我们记 分别为 的近似值。
在下面的计算过程中,我们需要定义关于 的离散二维Sine变换以及关于 的离散二维Sine逆变换,它们的形式分别如下
(2.29)
(2.30)
类似于一维的求解方法,在一个时间步长 上,假设 已知。采用时间分裂法,先求解方程(2.27)的非线性部分: ,利用共轭变换与定积分性质得:
(2.31)
作为时间分裂法的中间变量,即为第二部分的初始值。但是,等式右边仍然有未知量 。为了求解它,我们要利用方程 ,记 。对于上式做二维的Sine变换得: ,观察发现:等式右边可由已知函数 做二维的Sine逆变换求得;等式
左边出现了二阶导,利用关系式:
(2.32)
(2.33)
将上述两个关系式带入到方程 ,得
(2.34)
这样 就可求出,再利用一次二维的Sine变换就得到 。然后将其带入到方程(2.31)中,等式左边的中间变量 就可以表示出来,进而可以作为第二部分的初始值。
考虑线性部分: ,对于此方程,我们在时间方向上采用crank-nicolson法,空间上采用四
阶紧致差分格式来离散,具体如下:
(2.35)
对于(2.35),我们同时对等式两边做Sine变换得到:
(2.36)
等式右边的 ,可以由 做Sine逆变换得到。由于有关系式:
(2.37)
(2.38)
然后分别对 , 进行Sine变换,这样就可以得到 , 。所以等式(2.36)右边就可以当做已知,等式左边也是利用Sine逆变换及二维的Sine变换关系式,将其换算成只含有 。具体如下:
(2.39)
(2.40)
将上两式带入到等式(2.36)的左边,得到的就是一个只含有 的表达式,等式(2.36)的右边记为 。 综合等式(2.36)、等式(2.39)、等式(2.40)可得关系式:
(2.41)
由于等式右边均可知,所以就可求得 ,在利用一次Sine变换得 。这样时间方向上 就形成了完整迭代,然后利用MATLAB程序进行编写,称为计算法则2:
1) 输入a,b,c,d,T,M,N,L,β,以及 , , , ;
2) 计算 , , , , , , , 。 从 出发;
3) 计算 ,通过二维的Sine逆变换得 ,利用关系式:
(2.42)
再对 作二维的Sine变换得
4) 由 ,计算出 ;
5) 通过二维的Sine逆变换求出 ,再利用关系式(2.39),(2.40),求出 , ;
6) 最后由关系式(2.41),求出 ,对其作二维的Sine变换得 。再令 ,重复3~6直到 为止。
2.3. 三维非线性薛定谔泊松方程组的求解方法
考虑三维薛定谔泊松方程组:
(2.43)
(2.44)
其中 , , , , ,a,b,c,d,e,f,T,β均是给定常数, 已知函数,ϕ,ψ为未知函数。
首先,我们将区域[a, b]等分成M份,步长为 ;将区域[c, d]等分成N份,步长为 ;将区域[e, f]等分成P份,步长为 ;将区域[0, T]等分成L份,步长为 ;记 , 为 , 的近似值,其中 , , , , , , , 。
在下面的计算过程中,我们需要定义关于 的离散三维Sine变换以及关于 的离散三维Sine逆变换,它们的形式分别如下
(2.45)
(2.46)
下面讨论具体的求解过程。在时间方向上采用时间分裂法,在空间方向上采用基于快速Sine变换的四阶紧致差分格式。首先考虑在一个时间步长 上,假设 已知,然后将方程(2.43)分为两步求解:
1) 考虑非线性部分: ,利用共轭变换与积分性质得:
(2.47)
由于 是未知量,所以等式右边无法直接求出。考虑方程(2.44)类似于泊松方程, 我们采用基于Sine变换的四阶紧致差分格式来求解:
(2.48)
记 ,由基于Sine变换的四阶紧差分格式有如下关系式:
(2.49)
将上面三个等式带入到(2.48),得:
(2.50)
再利用一次Sine变换求出 ,这样对于时间分裂法的中间变量 就可以直接被表示出来。
2) 考虑线性部分方程的求解: ,其中 作为起始值,在时间方向上,采用crank-nicolson
来离散,在空间方向上采用基于Sine变换的四阶紧致差分格式来离散,具体如下:
对上式两边同时作Sine变换得:
(2.51)
这里
(2.52)
对于等式(2.51)的右边,只要对 做Sine逆变换得 ,再利用关系式:
就可以得到等式(2.51)右边的函数值。而对于等式(2.51)的左边,也利用关系式:
等式(2.51)就可化简为:
(2.53)
因此,形成了一个时间步长 上的一个完整迭代,具体实现步骤如下:
1) 输入a,b,c,d,M,N,P,L,e,f,T,β,以及 ,hx,hy,hz,τ;
2) 计算 , , , , , , , , , 。从 出发;
3) 计算 ,通过三维Sine逆变换得 ,利用关系式(2.50)求出 ,再做三维Sine变换得 ;
4) 由 ,计算出 ;
5) 通过三维Sine逆变换求出 ,利用 与 , , 的关系,求出(2.52)中的 ;
6) 利用方程(2.53)得 ,对其做三维Sine变换得 。再令 ,重复3~6直到 为止。
3. 数值计算例子
在前一节中,我们详细介绍了求解一维、二维、三维非线性薛定谔泊松方程组初边值问题的时间分裂紧致差分格式,并且介绍了如何分别利用一维离散Sine变换、二维离散Sine变换、三维离散Sine变换快速地求解离散后的系统。本节将介绍这些数值方法的计算结果。我们将利用两种紧致差分格式来进行计算:一种是四阶紧致差分格式(1.8),另一种是六阶紧致差分格式(1.10)。在上一节中,主要介绍关于四阶紧致差分格式(1.8)的算法。如果要利用六阶紧致差分格式(1.10)来离散方程中的二阶偏导数,那么需要将方程(1.14)中的右端参数变成方程(1.15)中的右端参数,算法中的其余过程不变。
3.1. 一维情形
考虑一维非线性薛定谔泊松方程组初边值问题(2.16)~(2.17),其中 , , ,
, 。通过改变空间步长h的大小做误差分析,在计算中我们取M = 512或空间步长 所得的近似解看作是方程的准确解 。我们通过第2.1节中所介绍的一维问题算法来求解,编写的代码在matlab软件中进行演算。误差定义 。
从表1中我们看出六阶紧致差分格式比四阶紧致差分格式得到的误差要小,二者在空间步长h较小时都能达到谱精度。图1显示粒子总数N(t)、冲量P(t)以及总能量E(t)不随时间变化而变化,从图1中可以看出我们提出的数值方法具有一定的数值守恒性。图2显示了密度函数 在不同时刻的图像。
3.2. 二维情形
考虑二维非线性薛定谔泊松方程组初边值问题(2.27)~(2.28),其中 ,
,初值函数为 。通过改变空间步长hx,hy的大小做误差分析,在计算中我们取 或空间步长 所得的近似解看作是方程的准确解 。我
们通过第2.2节中所介绍的二维问题算法来求解,编写的代码在matlab软件中进行演算。误差定义
。
Table 1. Error analysis of one-dimensional space calculation at time t = 1
表1. t = 1时刻的一维空间计算误差分析
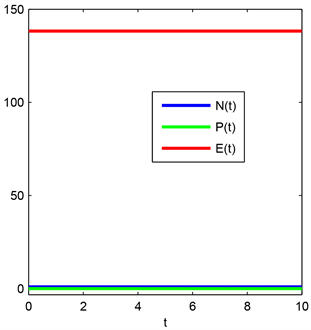
Figure 1. The trend of the total number of particles N(t), impulse P(t), and total energy E(t) over time
图1. 粒子总数N(t)、冲量P(t)以及总能量E(t)随时间变化的趋势
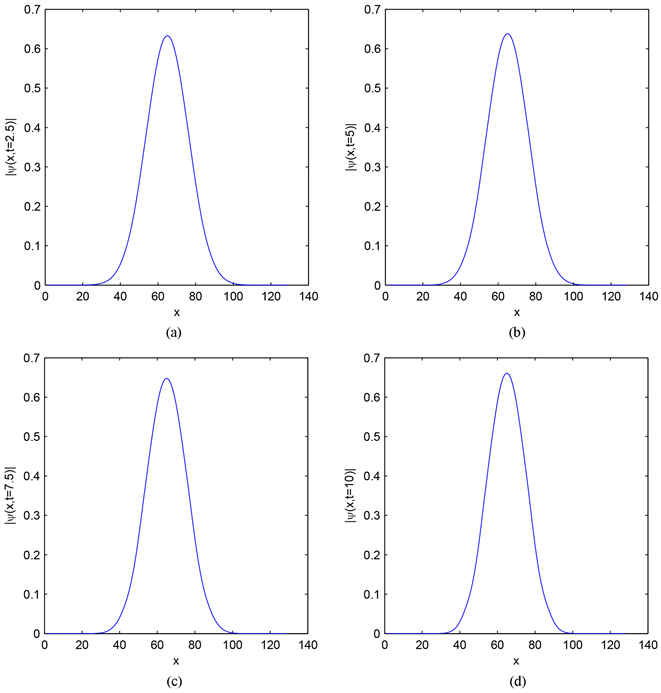
Figure 2. Image of density function at different times: (a) t = 2.5; (b) t = 5; (c) t = 7.5; (d) t = 10
图2. 密度函数 在不同时刻的图像:(a) t = 2.5;(b) t = 5;(c) t = 7.5;(d) t = 10
从表2中我们看出六阶紧致差分格式比四阶紧致差分格式得到的误差要小,二者在空间步长h较小时都能达到谱精度。图3显示粒子总数N(t)、冲量的分量Px(t)、冲量的分量Py(t)以及总能量E(t)不随时间变化而变化,从图3中可以看出我们提出的数值方法具有一定的数值守恒性。图4显示了密度函数 在t = 2.5、t = 5、t = 7.5、t = 10时的图像。
Table 2. Error analysis of two-dimensional space calculation at time t = 1
表2. t = 1时刻的二维空间计算误差分析
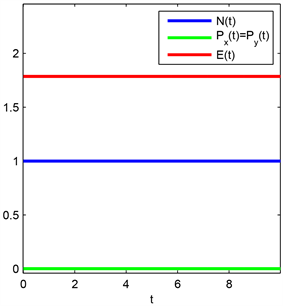
Figure 3. The trend of the total number of particles N(t), the component of the impulse Px(t) Py(t), and the total energy E(t) over time
图3. 粒子总数N (t)、冲量的分量Px(t)、Py(t)以及总能量E(t)随时间变化的趋势
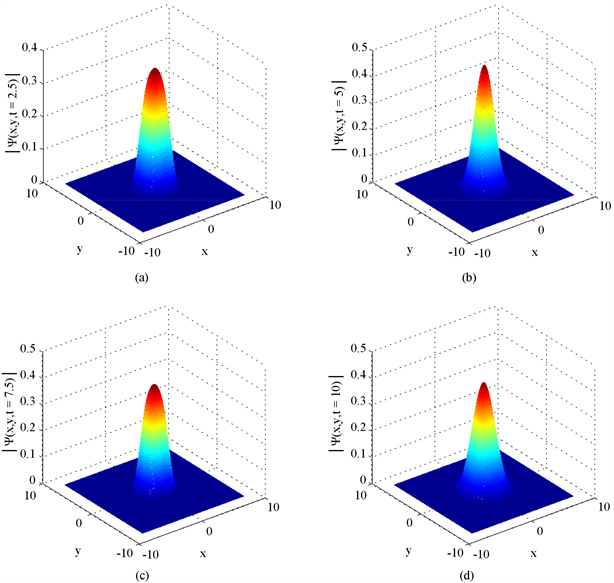
Figure 4. Image of density function at different times: (a) t = 2.5; (b) t = 5; (c) t = 7.5; (d) t = 10
图4. 密度函数 在不同时刻的图像:(a) t = 2.5;(b) t = 5;(c) t = 7.5;(d) t = 10
3.3. 3.3. 三维情形
考虑三维非线性薛定谔泊松方程组初边值问题(2.43)~(2.44),其中 , ,
,初值函数为 。通过改变空间步长hx,hy,hz的大小做误差分析,在计算中我们取 或空间步长 ,所得的近似解看作是方程的准确解 。我们通过2.2节中 所介绍的二维问题算法来求解, 编写的代码在matlab软件中进行演算。误差定义 。
从表2中我们看出六阶紧致差分格式比四阶紧致差分格式得到的误差要小,二者在空间步长h较小时都能达到谱精度。图5显示粒子总数N(t)、冲量的分量Px(t)、冲量的分量Py(t)、冲量的分量Pz(t)以及总能量E(t)不随时间变化而变化,从图5中可以看出我们提出的数值方法具有一定的数值守恒性。图6(a)、图6(c)分别显示了密度函数 在t = 5、t = 10的图像;图6(b)、图6(d)分别显示了密度函数 在t = 5、t = 10时的图像。
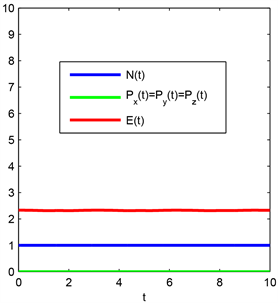
Figure 5. The trend of the total number of particles N(t), the component of the impulse Px(t), Py(t), Pz(t), and the total energy E(t) over time
图5. 粒子总数N(t)、冲量的分量Px(t)、Py(t)、Pz(t)以及总能量E(t)随时间变化的趋势
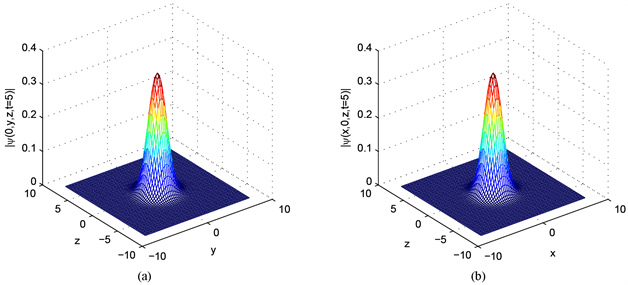
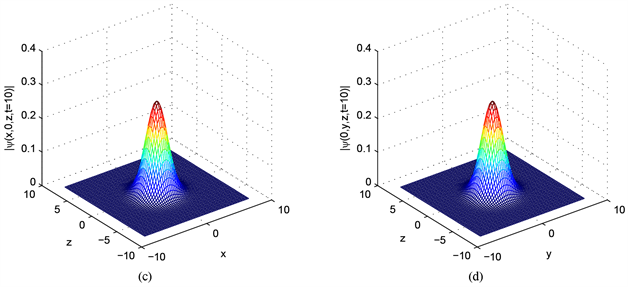
Figure 6. Density function images at different times: (a) t = 5, (c) t = 10; Density function images at different times: (b) t = 5, (d) t = 10
图6. 密度函数 在不同时刻的图像:(a) t = 5,(c) t = 10;密度函数 在不同时刻的图像:(b) t = 5,(d) t = 10
4. 结论
在本文中,我们主要讨论利用基于Sine变换的高阶紧差分格式、时间分裂法与Crank-Nicolson法结合的方法来求解非线性薛定谔–泊松方程组,借助离散傅里叶变换来实现Sine变换。最后,通过Matlab软件写出的程序计算出准确解与数值解的误差,画出误差分析图表以及在不同时刻未知函数的近似值。基于快速离散Sine变换的数值算法优点是计算程序简化,可以用较少的计算量达到相同的精确度,这也是我们在求解一些偏微分方程的过程中所期望的。随着当今科技与社会的进步,计算机的广泛应用,简单的求解方程的数值解已经无法满足了,快速和高效的数值解法就显得很有必要。
基金项目
本文受国家自然科学基金(91430103)资助。
文章引用
姜 珊,刘荣华,马 秀,王汉权. 求解薛定谔–泊松方程组的时间分裂紧致差分格式
Time-Splitting Compact Difference Scheme for Solving Schrodinger-Poisson Equations[J]. 应用数学进展, 2019, 08(01): 7-25. https://doi.org/10.12677/AAM.2019.81002
参考文献
- 1. Anderson, D., et al. (2002) Statistical Effects in the Multistream Model for Quantum Plasmas. Physical Review E, 65, 046417. https://doi.org/10.1103/PhysRevE.65.046417
- 2. Ben Abdallah, N. (2000) On a Multidimensional Schrödinger-Poisson Scattering Model for Semiconductors. Journal of Mathematical Physics, 41, 4241-4261. https://doi.org/10.1063/1.533397
- 3. Shukla, P.K. and Stenflo, L. (2006) Stimulated Scattering Instabilities of Electromagnetic Waves in an Ultracold Quantum Plasma. Physics of Plasmas, 13, Article ID: 044505. https://doi.org/10.1063/1.2196248
- 4. Shukla, P.K. and Eliasson, B. (2007) Nonlinear Interactions between Electromagnetic Waves and Electron Plasma Oscillations in Quantum Plasmas. Physical Review Letters, 99, Article ID: 096401.
- 5. Ashcroft, N.W. and Mermin, N.D. (1976) Solid State Physics. Saunders College Publishing, Orlan-do.
- 6. Lange, H., Toomire, B. and Zweifel, P.F. (1995) An Overview of Schrödinger-Poisson Problems. Reports on Mathematical Physics, 36, 331-345. https://doi.org/10.1016/0034-4877(96)83629-9
- 7. Markowich, P.A., Ringhofer, C.A. and Schmeiser, C. (1990) Semiconductor Equations. Springer, Berlin. https://doi.org/10.1007/978-3-7091-6961-2
- 8. Davydov, A.S. (1979) Solitons in Molecular Systems. Physica Scripta, 20, 387-394. https://doi.org/10.1088/0031-8949/20/3-4/013
- 9. Cheng, C., Liu, Q., Lee, J. and Massoud, H.Z. (2004) Spectral Element Method for the Schrödinger-Poisson System. Journal of Computational Electronics, 3, 417-421. https://doi.org/10.1007/s10825-004-7088-z
- 10. Dong, X. (2011) A Short Note on Simplified Pseudospectral Methods for Computing Ground State and Dynamics of Spherically Symmetric Schrödinger-Poisson-Slater System. Journal of Computational Physics, 230, 7917-7922. https://doi.org/10.1016/j.jcp.2011.07.026
- 11. Shaikh, D. and Shukla, P.K. (2008) 3D Electron Fluid Turbulence at Nanoscales in Dense Plasmas. New Journal of Physics, 10, Article ID: 083007. https://doi.org/10.1088/1367-2630/10/8/083007
- 12. Mauser, N.J. and Zhang, Y. (2014) Exact Artificial Boundary Condition for the Poisson Equation in the Simulation of the 2D Schrödinger-Poisson System. Computer Physics Communications, 16, 764-780. https://doi.org/10.4208/cicp.110813.140314a
- 13. Moroz, I., Penrose, R. and Tod, P. (1998) Spherical-ly-Symmetric Solutions of the Schrödinger-Newton Equations. Classical and Quantum Gravity, 15, C2733-C2742. https://doi.org/10.1088/0264-9381/15/9/019
- 14. Brezzi, F. and Markowich, P.A. (1991) The Three-Dimensional Wigner-Poisson Problem: Existence, Uniqueness and Approximation. Mathematical Methods in the Applied Sciences, 14, 35-61. https://doi.org/10.1002/mma.1670140103
- 15. Castella, F. (1997) L2 Solutions to the Schrödinger-Poisson System: Existence, Uniqueness, Time Behavior, and Smoothing Effects. Mathematical Models and Methods in Applied Sciences, 7, 1051-1083. https://doi.org/10.1142/S0218202597000530
- 16. Bao, W. and Cai, Y. (2013) Mathematical Theory and Numerical Methods for Bose-Einstein Condensation. Kinetic and Related Models, 6, 1-135. https://doi.org/10.3934/krm.2013.6.1
- 17. Bao, W., Mauser, N.J. and Stimming, H.P. (2003) Effective One Particle Quantum Dynamics of Electrons: A Numerical Study of the Schrödinger-Poisson- Model. Communications in Mathematical Sciences, 1, 809-831. https://doi.org/10.4310/CMS.2003.v1.n4.a8
- 18. Haas, F., Manfredi, G. and Feix, M. (2000) Multistream Model for Quantum Plasmas. Physical Review B, 62, 2763. https://doi.org/10.1103/PhysRevE.62.2763
- 19. Manfredi, G., Haas, F. (2001) Self-Consistent Fluid Model for a Quantum Electron Gas. Physical Review B, 64, 075316. https://doi.org/10.1103/PhysRevB.64.075316
- 20. 王芳芳. 紧致差分格式的理论及其分析[D]: [硕士学位论文]. 沈阳: 东北大学, 2010: 5-17.
- 21. Zhang, Y. (2013) Optimal Error Estimates of Compact Finite Difference Discretizations for the Schrödinger-Poisson System. Communications in Computational Physics, 13, 1357-1388. https://doi.org/10.4208/cicp.251011.270412a
- 22. 张勇. 薛定谔–泊松方程组的数值计算和分析及其应用[D]: [博士学位论文]. 北京: 清华大学, 2012: 2-23.
- 23. Lele, S. (1992) Compact Finite Difference Scheme with Spectral-Like Resolution. Journal of Computational Physics, 103, 16-42.
- 24. Wang, Y. and Lu, X. (2014) Modulational Instability of Electrostatic Acoustic Waves in an Electron-Hole Semiconductor Quantum Plasma. Physics of Plasmas, 21, Article ID: 022107. https://doi.org/10.1063/1.4864329
- 25. Wang, H., Zhang, Y., Ma, X., Qiu, J. and Liang, Y. (2016) An Efficient Implementation of Fourth-Order Compact Finite Difference Scheme for Poisson Equation with Dirichlet Boundary Conditions. Computers & Mathematics with Applications, 71, C1843-C1860. https://doi.org/10.1016/j.camwa.2016.02.022
