Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33743
,
6
pages
10.12677/AAM.2020.91002
Some Metric Properties in α-Lüroth Expansions
Bixuan Li, Sha Lan, Luming Shen
Information Science and Technology College of Hunan Agricultural University, Changsha Hunan
Received: Dec. 9th, 2019; accepted: Dec. 26th, 2019; published: Jan. 2nd, 2020

ABSTRACT
For the α-Lüroth expansion, some metric properties, such as “0-1” law, iterated logarithm law of the digits are studied in this paper. As the extension of alternating-Lüroth expansion, the conclusions in this paper include those of alternating-Lüroth case.
Keywords:α-Lüroth Expansion, “0-1” Law, Iterated Logarithm Law

α-Lüroth展式若干度量性质
李碧璇,兰 莎,沈陆明
湖南农业大学信息科学技术学院,湖南 长沙

收稿日期:2019年12月9日;录用日期:2019年12月26日;发布日期:2020年1月2日

摘 要
对于α-Lüroth展式,在此篇文章我们研究了α-Lüroth展式的一些度量性质,获得了该展式数字“0-1”律,基于该结果,得到了相应的重对数律,进一步完善了该展式的度量性质。作为交错Lüroth展式的推广,该论文的结论包括了交错Lüroth的相应的结果。
关键词 :α-Lüroth展式,“0-1”律,重对数律

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对单位区间上的划分 ,定义α-Lüroth映射 为:
。
这里
为 的Lebesgue测度,
,并且规定
依次从左至右顺序排列的为左开右闭区间。按照该算法,任意的
,均可以展成如下形式的α-Lüroth展式:
的Lebesgue测度,
,并且规定
依次从左至右顺序排列的为左开右闭区间。按照该算法,任意的
,均可以展成如下形式的α-Lüroth展式:
,
这里,如果 ,则 ,并且,如果对某个x满足 ,则 为有限序列,除 外,有限序列的最后一项大于或等于2的整数。为了简便,我们通常用 表示有限α-Lüroth,用 表示无穷展式。
对于该展式,一些基本的度量性质,如增长速度,逼近速度和数字频率可以通过Birkhoff’s定理 [1] 得到。Lüroth和交替Lüroth的情形就像连分式一样 [2] - [7]。在本文中,我们考虑α-Lüroth展式“0-1”率和重对数率。
定理1.1 令 是指数 的展式, 是定义于 上的正值函数,则:
1) 如果
发散,则
,即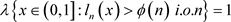 。
。
2) 如果 收敛,则 。
对任意的 ,令
。
定理1.2 令 是指数 的展式,对几乎处处的 ,有:
,
。
定理1.3 令 是指数 的展式,对几乎处处的 ,有:
,
。
在整篇文章中,我们用 表示Lebesgue测度, 表示取整数部分, 表示一个集合的直径。
2. 准备工作
本节主要讨论α-Lüroth展式的一些基本性质。如需了解更多关于α-Lüroth展式的结果,可见参考文献 [1] [8]。
定义2.1 对每一个k阶正整数数组 ,定义α-Lüroth展式第n个柱集为:
。
定义2.2 令 是一个可数的单位分割,则:
1) 若对于 ,有 ;则 是扩张的;
2) 如果分割
的尾部满足幂律,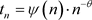 ,其中
是一个缓变函数,则
是指数
的指数扩张的;
,其中
是一个缓变函数,则
是指数
的指数扩张的;
3) 如果n充分大,我们有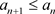 ,则分割
最终是递减的。
,则分割
最终是递减的。
引理2.1 对任意的 ,有:
,
这里 表示Lebesgue测度。
引理2.2 令 是指数 且递减的扩张分割。对任意的 ,存在 ,使得当满足对于任意的整数 ,有:
, (2.1)
和
。 (2.2)
引理2.3 令 是满足 的分割,则
。
为了简单起见,我们可以假设(2.1)和(2.2)对于所有 有分割 从跳跃开始减小,即对于所有 有 。这并不影响本文的研究。
3. 主要结果的证明
3.1. 定理1.2的证明
我们令 ,对于任意的k满足 ,这里我们有 和 ,反之我们有 。我们令
。
注意到 ,我们研究右上级数的收敛性。
根据Rabbe判别法,我们可以有 。
通过定理1.1,我们可以推断出如下的结论,
。
则,我们可以有
,
考虑到右端序列满足以 为子序列。
可以推断 ,因此,我们推断出以下结果:
。
然后,我们令 ,和前面的一样我对门得到关于 的结论。
。
因此,我们有
。
3.2. 定理1.3的证明
为了证明序列 的下限,我们首先得到同样的结论,
。
当 时,证明过程是相同的。然后,我们给出 的“0-1”比率。
我们回想起在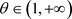 条件下定义的集合
,我们定义序列
条件下定义的集合
,我们定义序列
。
对于任意的 ,取 ,我们定义 ,回忆等式,我们有
。
因此,根Fatou引理,我们推断,
。
这里,我们取 为 的子序列。因此,我们用下面的方法计算上限,
。
因此,我们有
。
对于任意的 ,我们有
。
为了计算极限,我们假设 。我们定义
。
因此,我们有
。
注意到这一点,
,
我们取满足 和 的 ,其中 。
因此,
。
根据定理1.1,我们有
。
我们得到了
。
对于任意的 和 ,我们有
。
当时 ,这就是交替Lüroth展式的情形。
基金项目
这项工作得到了湖南农业大学大学生创新性实验计划项目(编号SCX1802)的支持。
文章引用
李碧璇,兰 莎,沈陆明. α-Lu¨ roth展式若干度量性质
Some Metric Properties in α-Lu¨ roth Expansions[J]. 应用数学进展, 2020, 09(01): 12-17. https://doi.org/10.12677/AAM.2020.91002
参考文献
- 1. Munday, S. (2012) Finite and Infinite Ergodic Theory for Linear and Conformal Dynamical System. University of St. Andrews, UK.
- 2. Galambos, J. (1974) An Iterated Logarithm Type Theorem for the Largest Coefficient in Continued Fractions. Acta Arithmetica, 25, 359-364.
https://doi.org/10.4064/aa-25-4-359-364 - 3. Khintchine A. Ya (1964) Continued Fractions. Chicago University Press, Chicago.
- 4. Kalpazidou, S., Knopfmacher, A. and Knopfmacher, J. (1991) Metric Properties of Alternating Lüroth Series. Portugaliae Mathematica, 48, 319-325.
- 5. Schweiger, F. (1995) Ergodic Theory of Fibred Systems and Metirc Number Theory. Clarendon Press, Oxford.
- 6. Dajani, K. and Kraaikamp, C. (1996) On Approximation by Lüroth Series. Journal de Théorie des Nombres de Bordeaux, 8, 331-346.
https://doi.org/10.5802/jtnb.172 - 7. Oppenheim, A. (1972) The Representation of Real Numbers by Infinite Series of Rationals. Acta Arithmetica, 21, 391-398.
https://doi.org/10.4064/aa-21-1-391-398 - 8. Kesseböhmer, K., Mundays, S. and Stratmann, B.O. (2012) Strong Renewal Theorems and Lyapunov Spectra for α-Farey and α-Lüroth Systems. Ergodic Theory and Dynamical Systems, 32, 989-1017.
https://doi.org/10.1017/S0143385711000186