¹温州大学，数理学院，浙江 温州

²温州大学，生命与环境科学学院，浙江 温州

收稿日期：2021年1月7日；录用日期：2021年2月11日；发布日期：2021年2月18日

摘要

基于“综合除藻 + 生态抑藻”相结合治理措施，构建了一类依赖状态反馈控制的藻–鱼生态系统，对其相关动力学特征进行理论分析与数值模拟，获得了系统半平凡周期解与周期解存在及其稳定的阈值条件，模拟出系统所具有的特定动力学性态，验证了理论推导结果的可行性与有效性，并进一步揭示综合治理措施的可实施性，这些研究工作为进一步探索亚热带水库蓝藻水华的综合治理提供一定的理论基础。

关键词

藻类种群，滤食性鱼类种群，平衡点，周期解，稳定性

Dynamics Analysis of an Algae-Fish Ecosystem Based on State Feedback Control

Fangfang Chen¹, Ziyou Zhuang¹, Xinyi Jiang¹, Hui Liu¹, Yichen Jiang¹, Chaoyue Huang¹, Qi Wang², Hengguo Yu^1*

¹School of Mathematics and Physics, Wenzhou University, Wenzhou Zhejiang

²School of Life and Environmental Sciences, Wenzhou University, Wenzhou Zhejiang

Received: Jan. 7^th, 2021; accepted: Feb. 11^th, 2021; published: Feb. 18^th, 2021

ABSTRACT

In the paper, on the basic of the combination of comprehensive algae removal and ecological algae suppression, an algae-fish ecosystem based on state feedback control was proposed to investigate the dynamic characteristics mathematically and numerically. The threshold conditions for the existence and stability of semi trivial periodic solution and periodic solution were obtained. The specific dynamic behaviors of the system were simulated to verify the feasibility and validity of the theoretical results and further reveal the feasibility of comprehensive management measures. Finally, it is our expectation that these studies can provide a theoretical basis for further exploring the comprehensive management of cyanobacterial blooms in subtropical reservoirs.

Keywords:Algae Population, Filter-feeding Fish Population, Equilibrium Point, Periodic Solution, Stability

Copyright © 2021 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

藻类水华暴发是亚热带湖库水体富营养化的重要表征现象之一，目前对其治理控制方法可分为物理法、化学法和生物法，它们各有优点，也有一定的局限性。因此，单独采用单一的方法治理极其复杂的水华生态系统是非常困难的，也很难到达理想的效果。以至于目前大多采用“综合除藻 + 生态抑藻”相结合的原则进行治理藻类水华，也就是前期采用物理打捞与喷射技术除藻，后期采用投放微生物制剂、构建生态浮床、放养滤食性鱼类等众多生物控藻法，去除湖库蓝藻水华现象 [1]。生物控制藻类水华是以底栖、滤食性鱼类控制藻类种群生长的一种生物调控方法，它是根据水生食物链生物之间的捕食关系，改变生物群落结构，增加对蓝藻种群的牧食压力，从而减低水体中藻类种群的生物量。目前鲢鱼和鳙鱼对蓝藻种群的牧食特性关注比较突出 [1] [2]。

就目前而言，无论用什么方法治理蓝藻水华，都是外界对自然水域生态系统的人为干扰，这种干扰行为既不是连续的，也不是离散的，而是两种并行存在的。同时，人类对自然资源的开发利用与经济管理既是离散的，又是瞬间完成的，会瞬间破坏原有生态系统的内在原始运行规律。为了把这些现实性问题转化为抽象性问题，借助现有数学工作对其更深刻的认识，可以借助半连续动力系统来刻画这些外界人为干扰现象对原有生态系统的影响机制。半连续动力系统在自然生态系统中得到了大量的应用，已经取得了一些不错的研究成果 [3] - [12]。论文 [4] 研究了一类基于状态反馈控制的捕食生态脉冲动力系统的动力学性态，理论推导出系统半平凡周期解的存在性和稳定性，数值模拟出系统相应的动力学行为。论文 [6] 构建了一类具有状态反馈控制的捕食生态脉冲动力系统，对其进行相关动力学理论与数值模拟，证明了半平凡周期解和正阶1周期解存在性和稳定性，研究结果揭示了正阶1周期解通过一个褶皱分岔从半平凡周期解分支出来。论文 [7] 探讨了一类状态反馈控制脉冲动力系统的阶1周期解的存在性问题，推导出系统阶1周期解存在的充分条件，并进一步得到了一种新的稳定性判定方法。论文 [8] 建立了一类捕食脉冲控制生态系统，利用类Poincaré准则得到了半平凡周期解存在和稳定的充分条件，证明了正周期解通过跨临界分岔从半平凡周期解分岔而来，提出了一种脉冲状态反馈控制策略来保证两种群的持续性。论文 [11] 假设当害虫数量达到一定阈值时，将采取害虫管理策略来控制害虫，因此提出了一种具有非线性状态反馈控制的害虫管理模型，对其相关动力学性态进行理论分析与数值仿真，研究模型的奇异性与周期解的稳定性。论文 [12] 构建了一类具有状态依赖脉冲收获的比率依赖食饵–捕食者生态模型，利用半连续动力系统的几何理论得到了一阶同宿环的存在性，并以 $\alpha$ 为控制参数，讨论了系统阶1周期解的存在性和稳定性，还调查了系统表现出关于参数 $\alpha$ 的同宿分岔现象。论文 [13] 研究了半连续动力系统同宿分支问题，讨论了一阶周期解的存在性和半连续动力系统的旋转向量场。论文 [14] 调查了一类依赖比率状态脉冲控制的食饵–捕食者模型的全局动力学行为，证明了系统的边界平衡点是全局渐近稳定的，利用brouwer不动点定理得到了一个阶k周期轨道。论文 [15] 探析了一类具有比率依赖状态脉冲控制策略的植物病害模型的动力学行为，研究发现当基本传染数大于1且地方病平衡点位于脉冲控制策略之上时，可以得到唯一的k阶周期解和介于1阶和2阶周期解之间的临界值。论文 [16] 首次利用广义脉冲响应函数对捕食–被捕食生态系统进行建模，在广义脉冲响应函数下建立了食饵消灭周期解的局部和全局稳定性的充分条件，在局部渐近稳定条件下，利用“一般脉冲响应函数”建立的定理推论与前人的结论非常一致，且以典型的脉冲响应函数(holling type-ii)为例验证了本文所得到的理论结果，结果表明与先前报道的结果是一致的。综上所知，半连续动力系统在生态种群动力学问题方面已经得到了广泛的应用，获得了一些比较有意义的理论结果，但是遗憾的是在水域生态系统的应用还是比较少的。

2. 依赖状态反馈控制的藻–鱼生态模型构建

基于亚热带水库藻类水华暴发情况与吴家园水库藻类水华综合治理情况，构建一类依赖状态反馈控制的藻类–鱼生态模型。首先给出以微分动力系统为基础的藻–鱼生态模型，可以表述如下：

$\{\begin{array}{l}\frac{\text{d}X}{\text{d}T}=r_{1}X\left(1-\frac{X}{k_1}\right)\left(\frac{X}{m_1}-1\right)-\frac{XY}{a_1+b_{1}X+X^2},\\ \frac{\text{d}Y}{\text{d}T}=\frac{{\mu }_{1}XY}{a_1+b_{1}X+X^2}-d_{1}Y,\end{array}$ (2.1)

其中 $X\left(T\right)$ ， $Y\left(T\right)$ 分别表示微囊藻种群和滤食性鱼类种群在T时刻的密度或数量， $k_1>0$ 表示微囊藻种群的最大环境容纳量， $r_1$ 表示微囊藻种群的内禀增长率， $m_1$ 表示Allee阈值， ${\mu }_1>0$ 为滤食性鱼类对微囊藻种群的捕食率， $a_1>0$ 是功能反应函数中的半饱和常数；对于非负 $X\left(T\right)$ 和 $b_1>-2\sqrt{a_1}$ ，参数 $b_1$ 使上述系统(2.1)的分母不消失； $d_1$ 表示滤食性鱼类种群的死亡率。

令 $X=k_{1}x$ ， $Y=k_1^2{r}_{1}y$ ， $T=\frac{t}{r_1}$ ，利用这些等量代换可将系统(2.1)无量纲化为下列微分方程：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)\left(mx-1\right)-\frac{xy}{a+bx+x^2},\\ \frac{\text{d}y}{\text{d}t}=\frac{\mu xy}{a+bx+x^2}-dy,\end{array}$ (2.2)

其中， $a=\frac{a_1}{k_1^2}$ ， $b=\frac{b_1}{k_1}$ ， $d=\frac{d_1}{r_1}$ ， $\mu =\frac{{\mu }_1}{k_1{r}_1}$ ， $m=\frac{k_1}{m_1}$ 且 $m>1$ 。

在系统(2.2)中选择微囊藻种群作为控制种群，这是因为当微囊藻种群的密度到达阈值h时，有暴发微囊藻水华的可能性，需要对微囊藻种群进行相关物理治理，因此我们假设物理治理的主要措施是对微囊藻种群进行收获打捞。同时，在对微囊藻种群打捞之后，释放滤食性鱼类进行生物控制，并要求既释放小鱼苗也要释放大鱼。因此，一类依赖状态反馈控制的藻类–鱼生态模型可以表述如下：

$\{\begin{array}{l}\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)\left(mx-1\right)-\frac{xy}{a+bx+x^2}\\ \frac{\text{d}y}{\text{d}t}=\frac{\mu xy}{a+bx+x^2}-dy\end{array}\}x\ne h,\\ \begin{array}{l}x=-px\\ y=qy+\tau \end{array}\}x=h,\end{array}$ (2.3)

其中， $\Delta x=x\left(t^{+}\right)-x\left(t\right)$ ， $\Delta y=y\left(t^{+}\right)-y\left(t\right)$ ， $p\in \left(0,1\right)$ 表示对微囊藻种群的收获率， $\tau >0$ 和 $q>0$ 分别表示滤食性鱼类种群的释放量和释放比率。

3. 理论分析

首先，系统(2.2)平衡点的存在性与稳定性。

令 $\{\begin{array}{l}x\left(1-x\right)\left(mx-1\right)-\frac{xy}{a+bx+x^2}=0,\\ \frac{\mu xy}{a+bx+x^2}-dy=0,\end{array}$

经过计算与定性分析可得到，当条件A满足时，系统(2.2)有三个边界平衡点 $E_0\left(0,0\right)$ ， $E_1\left(1,0\right)$ ， $E_2\left(\frac{1}{m},0\right)$ 和一个内平衡点 $E^{\text{*}}\left(x^{\text{*}},y^{\text{*}}\right)$ ，且内平衡点 $E^{\text{*}}\left(x^{\text{*}},y^{\text{*}}\right)$ 为鞍点，其中

$A:-\frac{d}{m^2}+\frac{\mu -bd}{m}-ad<0,\mu -\left(a+b+1\right)d>0,$

$x^{\text{*}}=\frac{\mu -bd+\sqrt{{\left(bd-\mu \right)}^2-4a{d}^2}}{2d},$

$y^{\text{*}}=\left(1-x^{\text{*}}\right)\left(m{x}^{\text{*}}-1\right)\left(a+b{x}^{\text{*}}+x^{\text{*}}{}^2\right).$

为了讨论系统(2.3)的特定动力学问题，需建立一个Poincaré映射，因此考虑系统(2.3)的向量场，令Poincaré截面为 $N=\left\{\left(x,y\right)|x=\left(1-p\right)h,y\ge 0\right\}$ ，且截面 $M=\left\{\left(x,y\right)|x=h,y\ge 0\right\}$ ，并假设 $\frac{1}{m}<\left(1-p\right)h<h<1$ 。可知直线 $x=\left(1-p\right)h$ 和 $x=h$ 与等倾线 $\left(1-x\right)\left(mx-1\right)-\frac{y}{a+bx+x^2}=0$ 分别相交于点 $A\left(\left(1-p\right)h,\left[1-\left(1-p\right)h\right]\left[mh\left(1-p\right)-1\right]\left[a+bh\left(1-p\right)+h^2{\left(1-p\right)}^2\right]\right)$ 和点 $B\left(h,\left(1-h\right)\left(mh-1\right)\left(a+bh+h^2\right)\right)$ ，直线 $x=\left(1-p\right)h$ 和 $x=h$ 与x轴分别交于点 $C\left(\left(1-p\right)h,0\right)$ 和 $D\left(h,0\right)$ 。令 $\Omega =\left\{\left(x,y\right)|0<y<\left(1-x\right)\left(mx-1\right)\left(a+bx+x^2\right),\left(1-p\right)h<x<h\right\}$ ，令 ${\Omega }_1=\Omega \cup \overline{CD}$ ，则当任意的点 $\left(x,y\right)\in \widehat{AB}$ 时，有 $\frac{\text{d}x}{\text{d}t}=0$ ，而当 $\left(x,y\right)\in \Omega$ 时， $\frac{\text{d}x}{\text{d}t}>0$ 。另外，在 $x=x^{\text{*}}$ 时， $\frac{\text{d}y}{\text{d}t}=0$ ，而当 $x<x^{\text{*}}$ 时， $\frac{\text{d}y}{\text{d}t}<0$ ；当 $x>x^{\text{*}}$ 时， $\frac{\text{d}y}{\text{d}t}>0$ 。此外，以任意点 $\left(x_0,0\right)\in \overline{CD}\subset {\Omega }_1$ 为初始点的轨线都保持 $y\left(t\right)=0$ 并且都趋向于 $\infty$ 。

其次，建立如下两个Poincaré映射：取N和M作为两个Poincaré截面。首先假设点 $A_{k-1}^{+}\left(\left(1-p\right)h,y_{k-1}^{+}\right)$ 在截面N上，根据上面对系统(2.3)向量场的分析可知，以点 $A_{k-1}^{+}$ 为初始点的轨线交截面M于点 $A_k\left(h,y_k\right)$ ，其中 $y_k$ 依赖于 $y_{k-1}^{+}$ 。令 $y_k=g\left(y_{k-1}^{+}\right)$ ，且点 $A_k$ 经过脉冲作用会跳到截面N上，并与截面N相交于点 $A_k^{+}\left(\left(1-p\right)h,\left(1+q\right)y_k+\tau \right)$ ，因此，得到如下Poincaré映射：

$P_0:y_k^{+}=\left(1+q\right)g\left(y_{k-1}^{+}\right)+\tau ,$ (3.1)

其次考虑另一个Poincaré截面。假设点 $A_k\left(h,y_k\right)$ 位于Poincaré截面M上，在脉冲作用下，点 $A_k\left(h,y_k\right)$ 跳到截面N上形成点 $A_k^{+}\left(\left(1-p\right)h,\left(1+q\right)y_k+\tau \right)$ ，以点 $A_k^{+}$ 为初始点的轨线交Poincaré截面M于点 $A_{k+1}\left(h,y_{k+1}\right)$ ，其中 $y_{k+1}$ 是与 $y_k$ 、参数q以及参数 $\tau$ 有关的，于是得到另一个Poincaré映射：

$P_1:y_{k+1}=g\left(\left(1+q\right)y_k+\tau \right)=F\left(q,\tau ,y_k\right),$ (3.2)

综上所述，得到两个Poincaré映射。

为了研究系统(2.3)的动力学性质，下面介绍两个引理。

引理3.1 [17] 设所研究状态反馈控制脉冲动力系统为

$\{\begin{array}{l}\begin{array}{l}\frac{\text{d}x}{\text{d}t}=P\left(x,y\right)\\ \frac{\text{d}y}{\text{d}t}=Q\left(x,y\right)\end{array}\}\varphi \left(x,y\right)\ne h,\\ \begin{array}{l}x=\alpha \left(x,y\right)\\ y=\beta \left(x,y\right)\end{array}\}\varphi \left(x,y\right)=h,\end{array}$ (3.3)

若条件 $\left|{\mu }_2\right|<1$ 成立，则系统(3.3)的一个T周期解 $x=\xi \left(t\right)$ ， $y=\eta \left(t\right)$ 是轨道渐近稳定的，其中 ${\mu }_2$ 是一个乘子，且有

${\mu }_2={\displaystyle \underset{k=1}{\overset{n}{\prod }}{\Delta }_k}\exp \left[{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\right],$

${\Delta }_k=\frac{P_{+}\left(\frac{\partial \beta }{\partial y}\cdot \frac{\partial \varphi }{\partial x}-\frac{\partial \beta }{\partial x}\cdot \frac{\partial \varphi }{\partial y}+\frac{\partial \varphi }{\partial x}\right)+Q_{+}\left(\frac{\partial \alpha }{\partial x}\cdot \frac{\partial \varphi }{\partial y}-\frac{\partial \alpha }{\partial y}\cdot \frac{\partial \varphi }{\partial x}+\frac{\partial \varphi }{\partial y}\right)}{P\left(\frac{\partial \varphi }{\partial x}\right)+Q\left(\frac{\partial \varphi }{\partial y}\right)},$

其中P，Q， $\frac{\partial \alpha }{\partial x}$ ， $\frac{\partial \alpha }{\partial y}$ ， $\frac{\partial \beta }{\partial x}$ ， $\frac{\partial \beta }{\partial y}$ ， $\frac{\partial \varphi }{\partial x}$ ， $\frac{\partial \varphi }{\partial y}$ 均表示函数在点 $\left(\xi \left(t\right),\eta \left(t\right)\right)$ 处的函数值，且 $P_{+}=P\left(\xi \left(t_k^{+}\right),\eta \left(t_k^{+}\right)\right)$ ， $Q_{+}=Q\left(\xi \left(t_k^{+}\right),\eta \left(t_k^{+}\right)\right)$ ， $\varphi \left(x,y\right)$ 是足够光滑且梯度不等于零的函数， $t_k\left(k\in N\right)$ 代表第k次发生脉冲作用的时间。

引理3.2 [18] 假设 $F:R\times R\to R$ 是一个单参数族映射，且满足以下条件：

1) $F\left(0,u\right)=0$ ，2) $\frac{\partial F}{\partial x}\left(0,0\right)=1$ ，3) $\frac{{\partial }^{2}F}{\partial x\partial u}\left(0,0\right)>0$ ，4) $\frac{{\partial }^{2}F}{\partial x^2}\left(0,0\right)<0$ 。

则映射F将在 $u=0$ 处发生跨临界分岔行为，若参数u的取值由负变正，则映射F的零不动点由稳定变为不稳定，并出现一个稳定的正不动点。

现在讨论系统(2.3)在什么条件下存在正周期解。

情况1： $\tau =0$

考虑系统(2.3)的一个子系统，此子系统只含微囊藻种群x，不含滤食性鱼类种群y。

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)\left(mx-1\right),x\ne h\\ \Delta x=-px,x=h\end{array}$ (3.4)

令初始值 $x_0=x\left(0\right)=\left(1-p\right)h$ ，由计算可得到系统(3.4)的一个解： $x\left(t\right)=\xi \left(t\right)$ ，其中 $\xi \left(t\right)$ 是方程 $\frac{{\left(m\xi \left(t\right)-1\right)}^m}{\xi {\left(t\right)}^{m-1}\left(1-\xi \left(t\right)\right)}=c{\text{e}}^{\left(m-1\right)\left(t-nT\right)}$ 一个解。令 $x\left(t\right)=T=\frac{\ln \left(\frac{\left(1-\left(1-p\right)h\right){\left(mh-1\right)}^m{\left(1-p\right)}^{m-1}}{\left(1-h\right){\left(m\left(1-p\right)h-1\right)}^m}\right)}{m-1}$ ，则 $x\left(T\right)=h$ ， $x\left(T^{+}\right)=\left(1-p\right)h$ ，因此，系统(2.3)具有半平凡周期解 $\left(\xi \left(t\right),0\right)$ ，可以表示如下：

$\{\begin{array}{l}x\left(t\right)=\xi \left(t\right),\\ y\left(t\right)=0,\end{array}$ (3.5)

其中 $nT<t\le \left(n+1\right)T$ ， $n\in N$ 。

定理3.1若 $0<q<{\left(1-p\right)}^d{M}_3^{-1}-1$ 成立，则系统(2.3)的半平凡周期解是轨道渐近稳定的。

证明：令 $P\left(x,y\right)=x\left(1-x\right)\left(mx-1\right)-\frac{xy}{a+bx+x^2}$ ， $Q\left(x,y\right)=\frac{\mu xy}{a+bx+x^2}-dy$ ， $\alpha \left(x,y\right)=-px$ ， $\beta \left(x,y\right)=qy$ ， $\varphi \left(x,y\right)=x-h$ ， $\left(\xi \left(T\right),\eta \left(T\right)\right)=\left(h,0\right)$ ， $\left(\xi \left(T^{+}\right),\eta \left(T^{+}\right)\right)=\left(\left(1-p\right)h,0\right)$ 。

根据引理，通过简单计算可得：

$\frac{\partial P}{\partial x}=\left(1-x\right)\left(mx-1\right)-x\left(mx-1\right)+mx\left(1-x\right)$ ， $\frac{\partial Q}{\partial y}=\frac{\mu x}{a+bx+x^2}-d$ ， $\frac{\partial \alpha }{\partial x}=-p$ ， $\frac{\partial \alpha }{\partial y}=0$ ， $\frac{\partial \beta }{\partial x}=0$ ， $\frac{\partial \beta }{\partial y}=q$ ， $\frac{\partial \varphi }{\partial x}=1$ ， $\frac{\partial \varphi }{\partial y}=0$ 。

$\begin{array}{c}{\Delta }_1=\frac{P_{+}\left(\frac{\partial \beta }{\partial y}\cdot \frac{\partial \varphi }{\partial x}-\frac{\partial \beta }{\partial x}\cdot \frac{\partial \varphi }{\partial y}+\frac{\partial \varphi }{\partial x}\right)+Q_{+}\left(\frac{\partial \alpha }{\partial x}\cdot \frac{\partial \varphi }{\partial y}-\frac{\partial \alpha }{\partial y}\cdot \frac{\partial \varphi }{\partial x}+\frac{\partial \varphi }{\partial y}\right)}{P\left(\frac{\partial \varphi }{\partial x}\right)+Q\left(\frac{\partial \varphi }{\partial y}\right)}\\ =\frac{P_{+}\left(\xi \left(T^{+}\right),\eta \left(T^{+}\right)\right)\left(1+q\right)}{P\left(\xi \left(T\right),\eta \left(T\right)\right)}\\ =\left(1+q\right)\left(1-p\right)\frac{\left[1-\left(1-p\right)h\right]\left[m\left(1-p\right)h-1\right]}{\left(1-h\right)\left(mh-1\right)}\end{array}$

可以得到：

$\begin{array}{l}\exp \left[{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\right]\\ =\exp \left[{\displaystyle {\int }_0^T\left(\left(1-\xi \left(t\right)\right)\left(m\xi \left(t\right)-1\right)-\xi \left(t\right)\left(m\xi \left(t\right)-1\right)+m\xi \left(t\right)\left(1-\xi \left(t\right)\right)\right)\text{d}t}\right]\\ =\exp {\displaystyle {\int }_{\left(1-p\right)h}^h[\frac{1}{\xi \left(t\right)}}-\frac{1}{1-\xi \left(t\right)}+\frac{m}{m\xi \left(t\right)-1}+\frac{\mu }{\left(1-\xi \left(t\right)\right)\left(m\xi \left(t\right)-1\right)\left(a+b\xi \left(t\right)+\xi {\left(t\right)}^2\right)}\\ -\frac{d}{\xi \left(t\right)\left(1-\xi \left(t\right)\right)\left(m\xi \left(t\right)-1\right)}]\text{d}\xi \left(t\right)\\ =M_1\end{array}$

从而得到：

$\begin{array}{c}{\mu }_2={\displaystyle \underset{k=1}{\overset{n}{\prod }}{\Delta }_k\exp \left[{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\right]}\\ =\left(1+q\right)\left(1-p\right)\frac{\left[1-\left(1-p\right)h\right]\left[m\left(1-p\right)h-1\right]}{\left(1-h\right)\left(mh-1\right)}\cdot M_1\\ =\left(1+q\right){\left(1-p\right)}^{-d}{M}_3\end{array}$

其中，

$M_1={\left(\frac{1-h}{1-\left(1-p\right)h}\right)}^{1+\frac{d}{m-1}-A}{\left(\frac{mh-1}{m\left(1-p\right)h-1}\right)}^{1+\frac{B}{m}-\frac{dm}{m-1}}{\left(\frac{h^2+bh+a}{{\left(1-p\right)}^2{h}^2+b\left(1-p\right)h+a}\right)}^{\frac{C}{2}}{\text{e}}^{M_2},$

$M_2=\frac{2D-bC}{\sqrt{4a-b}}\arctan \left(\frac{2\left[h\left(2-p\right)+b\right]}{4\left[a-h^2\left(1-p\right)\right]-b\left[2h\left(2-p\right)+b+1\right]}\right),$

$M_3={\left(\frac{1-h}{1-\left(1-p\right)h}\right)}^{\frac{d}{m-1}-A}{\left(\frac{mh-1}{m\left(1-p\right)h-1}\right)}^{\frac{B}{m}-\frac{dm}{m-1}}{\left(\frac{h^2+bh+a}{{\left(1-p\right)}^2{h}^2+b\left(1-p\right)h+a}\right)}^{\frac{C}{2}}{\text{e}}^{M_2},$

因此，当成立，则。根据引理3.1，则定理3.1成立。

注3.1：设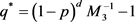，如果条件成立，则有，那么系统(2.3)可能发生分岔。如果成立，则系统(2.3)可能出现一个正周期解。

现在将讨论分岔的问题。首先分析的情况，考虑Poincaré映射(3.1)，设且u是充分小的非负数，映射(3.1)可化为如下形式：

(3.6)

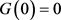其中函数是关于u和q的连续可微函数，且，则。

现在通过映射(3.6)和引理3.2，可得到定理3.2：

定理3.2当，，时，系统(2.3)发生跨临界分岔，当q由变化到时，系统会出现一个正不动点，当时，系统存在一个正周期解，其中。

证明：首先，根据引理3.2得知，需要计算出在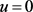处，和的值，其中，，令

(3.7)

其中，。

令为系统(2.3)的任意一条轨线，且，，，则有

(3.8)

由表达式(3.8)可得：

显然，，且有

(3.9)

进而可得，

(3.10)

其中，，。

由前面假设可知，在上有，可得：，显然，有，。由此可得：

. (3.11)

接下来验证满足引理3.2的所有条件。

1) 显然有，成立。

2) 由(3.9)可得：，进而得到：，这表明是对应于映射(3.6)的特征值为1的一个不动点。

3) 因为(3.9)成立，所以。

4) 最后，由(3.11)可知：。

综上所述，引理3.2的条件全部满足，因此定理3.2成立。

情况2：

现在将利用映射(3.2)来调查系统(2.3)正周期解的存在性。

定理3.3：设，则存在和使得成立，则系统(2.3)存在一个正阶1周期解，且。

证明：首先在Poincaré截面N上取一点，其中是一个充分小的正常数，且。以为初始点的轨线与截面M交于点，点在脉冲作用下跳到截面N上，交于点。以为初始点的轨线与截面M交于点。由充分小可知，，则表明点在点的上方，从而可知点在点的上方，即。由映射(3.2)可得，进而可以得到：

(3.12)

接下来假设垂直等倾线与Poincaré截面N的相交点为。以点A为初始点的轨线将交Poincaré截面M于点，那么就有，经过脉冲作用跳到点。推理可知，存在和使得成立，在这个时候，点和点A必然重合，系统(2.3)存在一个正的阶1周期解。当成立，则点位于点A的上方，根据轨线的不相交性可知，过点的轨线最终将趋于点，因而系统(2.3)不存在周期轨线。当成立，则点位于点A的下方，由于轨线的不相交性可知，以点为初始点的轨线与截面M将相交于点U下方的点处，即，则

(3.13)

由不等式(3.12)和(3.13)可知，Poincaré映射(3.2)具有一个不动点，即系统(2.3)有一个正的阶1周期解。

定理3.4 当时，设为系统(2.3)的一个正的阶1周期解，且初始点为，其中。如果条件成立，则是轨道渐近稳定的，其中

证明：设过点和周期解的周期为T，且。由于周期T的表达式是未知的，因此利用引理3.1来研究这个正阶1周期解的稳定性。此证明与定理3.2的不同之处在于：，，其他部分均相同，因此就有：

其中。

令，则有

若，即

(3.14)

则这个周期解是轨道稳定的，即当式子(3.14)成立时。

注3.2：由定理3.4可知，存在一个，当成立时，则有，因此系统(2.3)可能发生褶皱分岔。当成立时，系统(2.3)可能出现一个稳定的正阶2周期解，且随着q取值的增加，这个阶2周期解可能会有稳定变为不稳定。

4. 数值模拟与分析

为了深入探索综合治理蓝藻水华措施的有效性和验证数学理论结果的有效性，需要对系统的相关动力学特征进行模拟试验。依据模型建模假设与理论推导结果，系统相关参数取值分别为，因此可以得到系统的一个内平衡点为，所以选择状态控制参数，且选取初始值为。

当状态反馈控制参数时，依据定理3.1可知，系统(2.3)的半平凡周期解是轨道渐近稳定的，其结果如图1所示。这个数值模拟结果也暗示了当实施脉冲控制时，如果滤食性鱼类放养比例较小时，微囊藻种群生长动态模式是周期振荡，但是，滤食性鱼类种群将走向灭绝，不利于生态抑藻的实施。随着脉冲控制参数q取值的增加，也就是加大滤食性鱼类种群的放养量，即，则系统(2.3)将发生跨临界分岔，出现一个阶1正周期解，且这个阶1正周期解是稳定的，其结果如图2所示。这个数值仿真结果不但验证了定理3.2所得结果的可行性与有效性，而且说明增大滤食性鱼类种群放养量可以促进微囊藻种群与滤食性鱼类种群达到共存状态，且这种共存状态是以周期振荡的模型存在的，有利于滤食性鱼类种群的持久生存。进一步增加滤食性鱼类种群的放养量，但是这种放养主要是小鱼苗为主，

图1. 系统状态变量的相位图与时间序列图(半平凡周期解)

是为了维持生态经济管理而实施，即，系统(2.3)仍然拥有一个阶1正周期解(如图3所示)，也就是说微囊藻种群与滤食性鱼类种群仍然以周期振荡的模式共存，但是滤食性鱼类种群的生物量有所增加，微囊藻种群的生物量仍然要在可控范围内，这个数值仿真结果也验证了定理3.3和3.4的有效性。总而言之，基于上述数值仿真结果，验证了数学理论推导结果的可行性与有效性，揭示了状态反馈控制策略可以有效的控制微囊藻种群的生物量，也有利于滤食性鱼类种群与微囊藻种群的共存，且是以周期振荡模式达到共存状态，进而暗示了所建基于状态反馈控制的藻–鱼生态系统可以比较贴切地反映“综合除藻 + 生态抑藻”的综合治理策略的内在本质特征。

图2. 系统状态变量的相位图与时间序列图(阶1周期解)

5. 结论

就目前来说，亚热带水库蓝藻水华暴发频繁发生，相关管理部门在蓝藻水华暴发后，都会实施“综合除藻 + 生态抑藻”相结合治理措施，因此，为了探索这类综合治理措施的有效性与可行性，构建了一类依赖状态反馈控制的藻–鱼生态系统，对其相关动力学特征进行理论分析与数值模拟，证明了系统具

图3. 系统状态变量的相位图与时间序列图(阶1周期解)

有半平凡周期解与阶1周期解，推导出它们稳定的临界条件，数值模拟出半平凡周期解和阶1正周期解及其稳定趋势，验证了理论推导结果的可行性与有效性，推演出微囊藻种群与滤食性鱼类种群自然生长共存模式，进一步揭示这类综合治理措施的可实施性与可持续性，这些研究工作为进一步探索亚热带水库蓝藻水华的综合治理提供一定的理论基础。

基金项目

国家自然科学基金(61871293, 31570364, 41876124, 61901303)、国家重点国际合作项目(2018YFE0103700)、国家自然科学基金(31570364, 61871293, 41876124, 61901303)、浙江省重点研发项目(2021C03166)、苍南县科技计划项目(2018ZG29)和温州市科技重大专项(2018ZG002)。

文章引用

陈芳芳,庄子游,江欣怡,刘 慧,江逸城,黄超越,王 奇,于恒国. 一类基于状态反馈控制的藻–鱼生态系统的动力学分析
Dynamics Analysis of an Algae-Fish Ecosystem Based on State Feedback Control[J]. 应用数学进展, 2021, 10(02): 373-385. https://doi.org/10.12677/AAM.2021.102043

参考文献