Advances in Applied Mathematics
Vol.
10
No.
07
(
2021
), Article ID:
43716
,
10
pages
10.12677/AAM.2021.107236
基于模糊厌恶的最优投资与超额损失 再保险策略
谢奕,王伟
天津师范大学数学科学学院,天津

收稿日期:2021年6月5日;录用日期:2021年6月28日;发布日期:2021年7月7日

摘要
本文研究了保险公司对金融市场存在模糊厌恶情况下的最优投资与超额损失再保险策略。在最大化保险公司终端财富的目标下,采用指数效用函数,通过随机控制方法得到了最优投资与再保险策略以及值函数的表达式。最后通过数值算例分析了参数对最优投资与再保险策略的影响。
关键词
模糊厌恶,超额损失再保险,随机控制,最优再保险,最优投资
Optimal Investment and Excess-Loss Reinsurance Strategies Based on Ambiguity Aversion
Yi Xie, Wei Wang
School of Mathematical Sciences, Tianjin Normal University, Tianjin

Received: Jun. 5th, 2021; accepted: Jun. 28th, 2021; published: Jul. 7th, 2021

ABSTRACT
This paper studies the optimal investment and excess-loss reinsurance strategies for insurance companies with ambiguity aversion to financial market. Under the goal of maximizing the terminal wealth of insurance companies, the optimal investment and reinsurance strategies and the expression of value function are obtained by using stochastic control methods with exponential utility function. Finally, numerical examples are given to analyze the influence of some parameters on the optimal investment and reinsurance strategies.
Keywords:Ambiguity Aversion, Excess-Loss Reinsurance, Stochastic Control, Optimal Reinsurance, Optimal Investment

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,保险公司的再保险问题一直是精算学中的热点。当索赔发生时,保险公司无力承担全部的索赔额数目,于是选择了将其一部分风险转移出去给另外的保险公司,那么承担这部分风险的保险公司称为再保险公司,通过这种方法可以降低赔付的风险和提高经营稳定性。常见的再保险方式有比例再保险和超额损失再保险,如文献 [1] 考虑了动态比例再保险策略,并在一个扩散模型和一个经典风险模型中得到了最优策略;文献 [2] 研究了超额损失再保险控制问题,通过构造两类次优控制问题来求解最优控制问题并确定最优策略;文献 [3] 在控制过程的基础上加入固定成本和比例成本,再保险方式为超额损失再保险,通过用随机控制方法得到了值函数和最优策略的闭式解。
投资可以提高公司的竞争力,增强公司的偿付能力以提高公司效益和经营的稳定性,所以保险公司的投资也是必不可少的一部分。如文献 [4] 考虑了一个最优控制问题,其中风险资产用于投资,证明了该优化问题的有一个经典解,并且得到了保险公司的最优投资;文献 [5] 研究一般保险人在未来某一时刻准备金的指数效用最大化意义下的最优投资选择问题。
保险公司的再保险与投资问题的结合也是热门话题之一,如文献 [6] [7] [8] 中保险公司的目标是最大限度地提高指数效用的终端财富的期望,通过求解Hamilton-Jacobi-Bellman (HJB)方程得到最优投资与再保险策略。当保险公司要进行投资时,一定会对金融市场做一个评估,但是由于保险公司对金融市场的了解不一定全面以及金融市场具有复杂不受控的特点,所以会导致模糊性的产生。文献 [9] 研究了保险人在风险资产和保险风险带模糊的盈余模型下的最优稳健投资和再保险问题,求解HJB方程导出了值函数的显式解,并找到了最优投资与再保险策略;文献 [10] 在金融市场存在模糊性下研究保险公司的最优投资和最优保费策略,且其盈余过程为非线性扩散的。
本文考虑与文献 [10] 类似的模型,研究带模糊的最优投资与超额损失再保险策略,通过求解相应的HJB方程,得到最优投资与再保险策略以及值函数的表达式,最后给出了数值算例。
2. 模型建立
2.1. 再保险与投资模型
经典Cramer-Lundberg模型的盈余过程 为
其中 为初始盈余, 为保费收取速率, 是强度为 的Poisson过程, 是正的独立同分布随机变量,表示为索赔额。 与 之间相互独立,且有共同的分布函数 与有限的一阶矩和二阶矩。若采用期望保费准则,则有
其中 为保险人的安全负荷。
接下来考虑再保险问题。令 为超额损失自留额, 为保险人的第 次索赔。假设再保险人和保险人有相同的安全负荷,则加入再保险后的盈余过程为
(1)
其中 。不失一般性,假设 。由文献 [2],可以用扩散过程逼近式(1),则盈余过程为
(2)
其中 是一个标准布朗运动,且
(3)
(4)
考虑超额损失自留额 是一个动态可控参数,那么关于时间 ,有 ,则盈余过程(2)变为
(5)
假设保险人是风险厌恶型的,且有效用函数 使得 和 。为了使得所得最优投资与再保险策略的形式更加简洁,采用指数效用函数
(6)
其中 是绝对风险厌恶系数。
下面考虑投资问题。假设保险公司在金融市场投资两种资产,即无风险资产和风险资产。其中无风险资产的价格过程为
(7)
其中 为无风险利率。风险资产的价格过程为
(8)
其中 和 为常数,其中 是一个标准布朗运动,且通常要求 。假设金融市场与保险公司有相关性且用 来描述,即有 。为了方便计算,用一个与 相互独立的标准布朗运动 来表示,有
将上式代入式(8),有
假设保险公司在 时刻将资金 投到风险资产,那么考虑再保险控制 与投资策略 后的(5)变为
(9)
2.2. 金融市场的模糊性和值函数
对于以往的最优投资与再保险问题,必须要知道概率测度 的准确性才可以进行求解。然而,保险人通常是基于有限的信息和技术来估计 (参考模型),即保险公司对参考模型的认知不是完全准确的,所以参考模型对保险人来说是存在模糊的。因此,需要考虑其他的概率测度,即替代模型。假设保险人只对金融市场存在模糊性,且要求替代模型与参考模型等价。记所有满足条件的替代模型的集合为 ,由上可知若 ,则 ,“ ”表示等价。由 [11] 中的Girsanov定理,发现 满足
其中
为P-鞅且其域流为 ,并且满足Novikov条件
其中 为适应过程。由Girsanov定理,关于概率测度 的标准布朗运动 为
(10)
其中 为在概率测度下 的标准布朗运动。并且由Girsanov定理,知 在 下也为标准布朗运动,故 不会改变盈余过程(5)。为了在研究中考虑替代模型,用相对熵来度量替代模型和参考模型之间的差异。 和 的相对熵为
最后一个等式是由于 在 下为标准布朗运动。令 ,则可用 来衡量相对熵的
大小。由于参考模型是保险公司经过较多的经验与技术设计出来的,尽管存在模糊性,但是还是具有一定的参考价值,所以不使用参考模型而使用替代模型会有惩罚存在。显然,差异越大即相对熵越大,惩罚越大。
下面给出可行策略与其所满足的条件。
定义1如果 中的元素满足如下条件:
(i) 可料:
(ii) 可料并满足
其中 表示在概率测度 下的条件期望,那么称 为可行策略的集合。
与文献 [12] 类似,随机控制问题的值函数为
(11)
其中 , 为是一标准化函数其作用是把惩罚的量级转化成与 同样的
数量级来惩罚, 表示保险公司对参考模型的信任程度。 越大,保险公司对参考模型越信任,此时若使用替代模型,保险公司则会面临越大的惩罚。inf代表保险公司对模糊的态度是厌恶的,sup表示公司目标是找到最优的投资与再保险策略。
注1 假设 。当 时,表示保险公司对参考模型十分信任,若此时使用替代模型则会面临巨大的惩罚,所以不会使用任何替代模型,即不含模糊性;当 时,表示保险公司对参考模型没有任何了解。
注2 式(12)中值函数 满足 ,,证明过程与文献 [13] 类似。即
是凹函数,说明保险人对模糊的态度是厌恶的。
3. 最优再保险和投资策略
为了解决问题(11),需要在 下考虑财富过程,即将式(10)代入式(9),有
(12)
对于可控策略 和任意函数 ,定义无穷小微分算子 为
(13)
其中 、 分别表示关于 的一、二阶导数。
由动态规划原理和文献 [12],可得到若 ,则值函数满足的HJB方程为
(14)
并且有边界条件 。
假设 ,选择合适的 来标准化惩罚的量级,有
(15)
将式(13)和(15)代入式(14),有
(16)
因为 ,由一阶条件,为满足式(16)的最小化,则 有
(17)
将式(17)代入式(16),有
(18)
接下来,通过求解式(18)得到最优策略与值函数的表达式。
定理1 如果保险人采用指数效用函数(6),对于任何 ,最优再保险和投资策略满足如下关系
值函数的形式为
其中 ,函数 的表达式为式(27)。
证明:首先,由式(6)和边界条件猜测值函数的形式为
其中 。由边界条件 ,可得 。然后,对 关于 和 分别
求偏导,有
(19)
(20)
(21)
将式(19)、(20)和(21)代入式(18),化简后可得到
(22)
由一阶条件、式(3)和(4),可以得到
(23)
(24)
将式(24)代入式(23),有
(25)
将式(24)代入式(22),整理有
(26)
结合由边界条件得到的 ,有
(27)
综上,式(24)、(25)和(27)为所求,即定理得证。
注3 定理1最优策略中的 简写为 。由于再保险方式为超额损失再保险,分布函数未知,所以最优策略中都含有 。
注4 由值函数 的表达式可以很容易的验证 。此外,由于
所以 满足Novikov条件。
4. 数值算例
本节中的式(3)和(4)采用指数分布,其分布函数为 ,其中 ,则尾分布 。将其带入式(3)和(4),有
下面研究参考模型的信任度 与相关系数 这两个参数对最优再保险与投资策略的影响,其他参数取值如下: ,,,,, (图4 )。
图1说明当 时,信任度 越大,最优投资越大,相反,随着信任度 增大,最优再保险变小;当 时,从图2可以看出信任度 值大小的变化对最优再保险的影响不显著,但对最优投资有影响, 越大,最优投资越大;当 时,从图3可以看出,信任度 越大,最优再保险和最优投资都增大。在图4中可以发现,在信任度 一定时,保险公司和金融市场的相关系数 越大,最优再保险越大,最优投资越小。
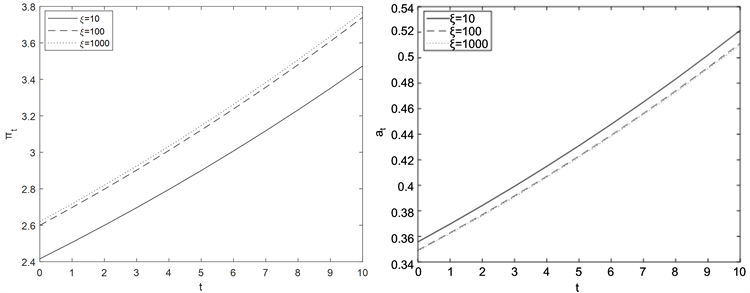
Figure 1. The influence of ξ on investment and reinsurance strategies when ρ = −0.3
图1. ρ = −0.3时,ξ对投资和再保险策略的影响
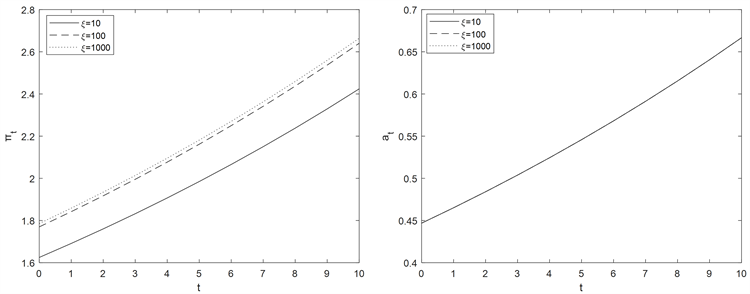
Figure 2. The influence of ξ on investment and reinsurance strategies when ρ = 0
图2. ρ = 0时,ξ对投资和再保险策略的影响
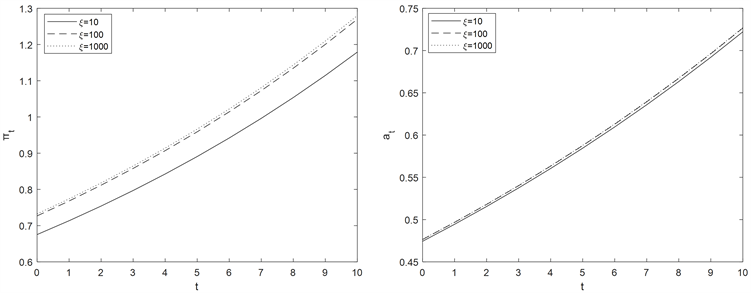
Figure 3. The influence of ξ on investment and reinsurance strategies when ρ = 0.3
图3. ρ = 0.3时,ξ对投资和再保险策略的影响
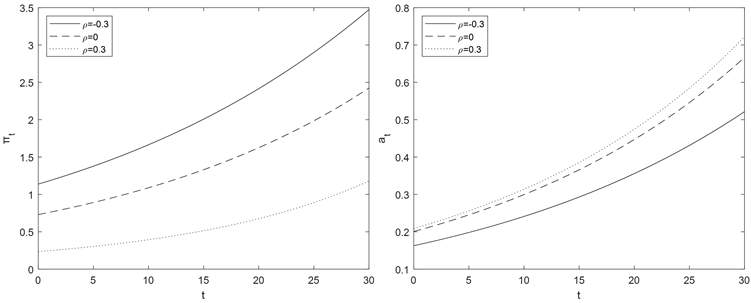
Figure 4. The influence of ρ on investment and reinsurance strategies when ξ = 10
图4. ξ = 10时,ρ对投资和再保险策略的影响
5. 结论
本文研究了带模糊厌恶的最优投资与再保险策略。对模型进行了扩散逼近,通过求解相应的HJB方程,得到了最优再保险和最优投资策略及值函数的显式表达式。最后,通过数值算例发现模糊性和金融市场与保险公司的相关性这两个因素对最优策略都有影响。此外,在本文的基础上还可以考虑采用其他效用函数,如对数效用函数、幂函数效用函数等。
基金项目
国家自然科学基金(11401436);天津市高等学校科技发展计划(JW1714)。
文章引用
谢 奕,王 伟. 基于模糊厌恶的最优投资与超额损失再保险策略
Optimal Investment and Excess-Loss Reinsurance Strategies Based on Ambiguity Aversion[J]. 应用数学进展, 2021, 10(07): 2268-2277. https://doi.org/10.12677/AAM.2021.107236
参考文献
- 1. Schmidli, H. (2001) Optimal Proportional Reinsurance Policies in a Dynamic Setting. Scandinavian Actuarial Journal, 1, 55-68. https://doi.org/10.1080/034612301750077338
- 2. Liu, W. and Hu, Y.J. (2014) Optimal Financing and Dividend Control of the Insurance Company with Excess-of-Loss Reinsurance Policy. Statistics and Probability Letters, 84, 121-130. https://doi.org/10.1016/j.spl.2013.09.034
- 3. Cheng, G.P., Wang, R.M. and Yao, D.J. (2014) Optimal Dividend and Capital Injection Strategy with Excess-of-Loss Reinsurance and Transaction Costs. Journal of Industrial and Management Optimization, 14, 371-395. https://doi.org/10.3934/jimo.2017051
- 4. Hipp, C. and Plum, M. (2003) Optimal Investment for Investors with State Dependent Income, and for Insurers. Finance and Stochastics, 7, 299-321. https://doi.org/10.1007/s007800200095
- 5. Wang, N. (2007) Optimal Investment for an Insurer with Exponential Utility Preference. Insurance: Mathematics and Economies, 40, 77-84. https://doi.org/10.1016/j.insmatheco.2006.02.008
- 6. Irgens, C. and Paulsen, J. (2004) Optimal Control of Risk Exposure, Reinsurance and Investments for Insurance Portfolios. Insurance: Mathematics and Economics, 35, 21-51. https://doi.org/10.1016/j.insmatheco.2004.04.004
- 7. Bai, L.H. and Guo, J.Y. (2008) Optimal Proportional Reinsurance and Investment with Multiple Risky Assets and No- Shorting Constraint. Insurance: Mathematics and Economics, 42, 968-975. https://doi.org/10.1016/j.insmatheco.2007.11.002
- 8. Lin, X. and Yang, P. (2011) Optimal Investmentand Reinsuranceina Jump Diffusion Risk Model. The ANZIAM Journal, 52, 250-262. https://doi.org/10.1017/S144618111100068X
- 9. Luo, S.Z., Wang, M.M. and Zhu, W. (2019) Maximizing a Robust Goal-Reaching Probability with Penalization on Ambiguity. Journal of Computational and Applied Mathematics, 348, 261-281. https://doi.org/10.1016/j.cam.2018.08.049
- 10. 刘兵, 周明. 模糊厌恶下的最优投资与最优保费策略[J]. 系统工程理论与实践, 2020, 40(7): 1707-1720.
- 11. Klebaner, F.C. (2008) Introduction to Stochastic Calculus with Applications. Imperial College Press, London.
- 12. Fleming, W.H. and Soner, H.M. (2006) Controlled Markov Processes and Viscosity Solutions. Springer, New York.
- 13. Zhou, M., Yuen, K.C. and Yin, C.C. (2017) Optimal Investment and Premium Control for Insurers with a Nonlinear Diffusion Model. Acta Mathematicae Applicatae Sinica, 33, 945-958. https://doi.org/10.1007/s10255-017-0709-7