Advances in Applied Mathematics
Vol.
11
No.
11
(
2022
), Article ID:
57384
,
9
pages
10.12677/AAM.2022.1111795
(1 + 1)-维Benjiamin Ono方程的 行波解及分岔
杨德牛
南昌应用技术师范学院,江西 南昌
收稿日期:2022年9月28日;录用日期:2022年10月21日;发布日期:2022年11月1日

摘要
本文借助平面动力系统分支理论和符号计算方法研究了(1 + 1)-维的Benjiamin Ono方程。首先经过行波变换得到二维的平面行波系统,借助Maple软件的符号计算得到了分岔的参数条件,同时给出了所有的分岔相图。利用平面行波系统的首次积分,把行波系统的求解转化为椭圆积分。然后讨论了在不同参数条件下所有精确解的解析表达式,包括周期波解、孤立波解,同时也给出了这些解的平面图像,通过图像可以很好的揭示其动力学行为。
关键词
孤立波解,周期波解,非线性发展方程,分岔

Bifurcation and Travelling Wave Solutions for the (1 + 1)-Dimensional Benjiamin Ono Equation
Deniu Yang
Nanchang Normal College of Applied Technology, Nanchang Jiangxi
Received: Sep. 18th, 2022; accepted: Oct. 21st, 2022; published: Nov. 1st, 2022

ABSTRACT
In the paper, the (1+1)-dimensional Benjiamin Ono equation is studied by means of bifurcation theory and method of plane dynamical systems. Firstly, the traveling wave system are obtained by traveling wave transformation. The parameter conditions of the bifurcation are obtained by the symbolic calculation of Maple software, and all the phase diagrams of the bifurcation are given. By using the first integral of a plane traveling wave system, the solution of the traveling wave system is transformed into an elliptic integral. Then, the analytical expressions of all the exact solutions under different parameters are discussed, including periodic wave solutions and solitary wave solutions. At the same time, the plane images of these solutions are given, which can reveal their dynamic behaviors well.
Keywords:Solitary Wave Solution, Periodic Wave Solution, Nonlinear Evolution Equation, Bifurcation

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非线性发展方程在众多学科的发展中起着十分重要的作用,在海洋、物理、数学以及工程领域的众多分支领域中,如海洋内波、非线性光学、流体力学、凝聚态物理、光纤通信等,非线性发展方程的很多理论被广泛的应用。国内外众多的学者在非线性发展方程的精确解,解的存在性,稳定性,分歧等方面取得了很多成果。例如文献 [1] [2] 分别讨论了Fisher方程的稳定性和动态分歧,精确解。文献 [3] 研究了Fisher-KPP方程的精确波前解。文献 [4] 则研究了时滞Fisher-KPP方程的行波解及其分岔。文献 [5] 借助修正的变分迭代方法研究了广义的Fisher方程。文献 [6] [7] 研究了非线性扩散的KPP方程的动力学性质。文献 [8] [9] 研究了KPP方程的动力学行为,其中 [8] 中研究了具有缓慢衰减初始条件的KPP方程的快速传播, [9] 中解释了KPP方程解的渐近性行为。文献 [10] 利用改进的辅助方程法,分别获得(1 + 1)维Benjiamin Ono方程,Phi-4方程,(3 + 1)维YTSF方程,foam drainage方程的精确解。文献 [11] [12] [13] 中研究了(1 + 1)-维的Benjiamin Ono方程的精确解,得到了一些不错的结果。本文将借助李继彬教授发展的平面动力系统分岔方法 [14] [15] 研究(1 + 1)-维的Benjiamin Ono方程,得到其行波解的相图、分岔的参数条件以及在不同参数条件下,得到了所有行波解的参数表达式,给出其解轨线的图像。这些结论将可以很好的补充现有的研究成果,帮助我们更好的理解(1 + 1)-维的Benjiamin Ono方程。
2. (1 + 1)-维的Benjiamin Ono方程的行波解分岔
2.1. (1 + 1)-维的Benjiamin Ono方程的相图、分岔
(1 + 1)-维的Benjiamin Ono方程,在物理学中起着非常重要的作用,其一般形式如下
(1)
引入如下行波变换
(2)
其中c表示行波的波速,且不妨假设 。代入(2)式到(1)式中得到二阶的常微分方程:
(3)
等式(3)左右两边关于变量 积分两次,得到:
(4)
引入 ,代入(4)式得到如下的平面行波系统:
(5)
行波系统(5)有如下首次积分:
(6)
其中h是哈密尔顿能量常数。行波系统(5)有两个平衡点 。现记
显然,容易知道:
(1) 当 时, ,此时平衡点 是鞍点,是不稳定的。
(2) 当 时, ,此时平衡点 是中心,是稳定的。
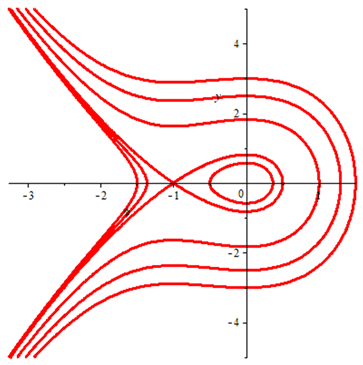
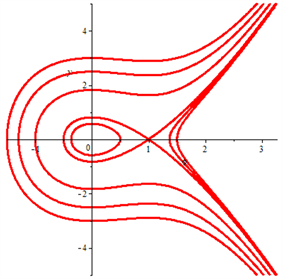
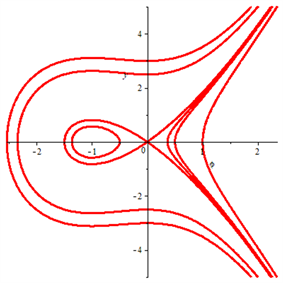
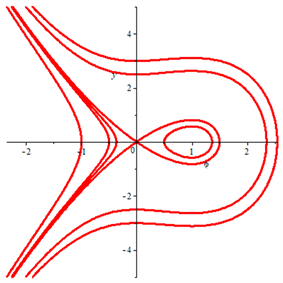
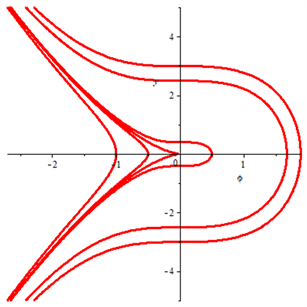
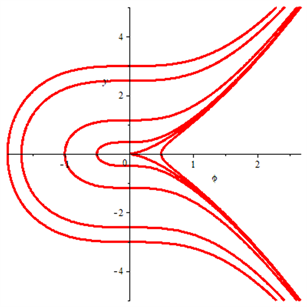
根据微分方程分岔理论和方法,可得平面行波系统(5)的分岔及相图如图1~6所示。
图1.
图2.
图3.
图4.
图5.
图6.
从图1~6可知:
(1) 当 时,平衡点 是鞍点,平衡点 是中心。
(2) 当 时,平衡点 是中心,平衡点 是鞍点。
(3) 当 时,行波系统(5)不存在有界行波解,所有的解都是奇异的,不具有物理学意义。
2.2. (1 + 1)-维Benjiamin Ono方程的精确行波解
由系统(5)的平面相图可以看出,围绕中心平衡点有一簇周期轨道,对应于方程(3)的周期波解。在鞍点处有一条同宿轨道,对应于方程(3)的孤立波解。
(i) 当 时,对应于相图1。
(1) 定义的是系统(5)的同宿轨线,此时
(7)
代入(7)式到系统(5)的第一式中,得到:
(8)
计算(8)式,得到孤立波解,取值 ,孤立波如图7所示。
. (9)
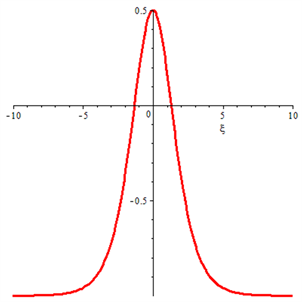
Figure 7. The solitary solution of Eq. (9)
图7. 孤立波解式(9)
(2) 当 时,此时定义的是系统(5)的一簇周期轨线,对应与系统(5)的周期波解,此时可得
(10)
代入(10)到系统(5)的第一式得到:
(11)
计算(11)式得到周期波解:
(12)
其中 是第一类的椭圆积分。取值 ,周期波如图8所示。
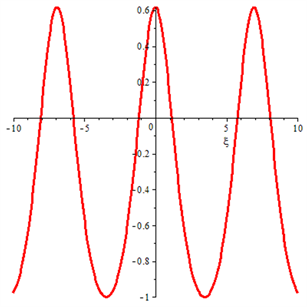
Figure 8. The periodic solution of Eq. (12)
图8. 周期波解式(12)
(ii) 当 时,对应于相图2。此时的相图跟(i)类似,只是开口方向相反。详细的计算过程在此就不再赘述,直接给出结论。
(1) 当 定义的是系统(5)的同宿轨线,对应于方程(3)的孤立波解,如下:
(13)
取值 ,孤立波如图9所示。
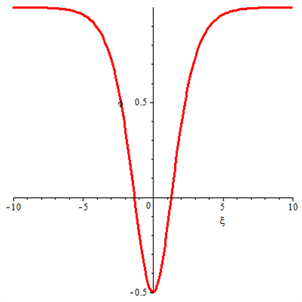
Figure 9. The solitary solution of Eq. (13)
图9. 孤立波解式(13)
(2) 围绕中心 的是一簇周期轨道,对应于方程(3)的周期波解,其精确解是式(12),此时 。
(iii) 当 时,对应于相图3。
(1) 当 时,定义的是系统(5)的同宿轨道,此时
(14)
代入式(14)到系统(5)中第一式,得到
(15)
由式(15)得到系统(5)的孤立波解如下:
(16)
取值 ,得到孤立波解的图像如图10所示。
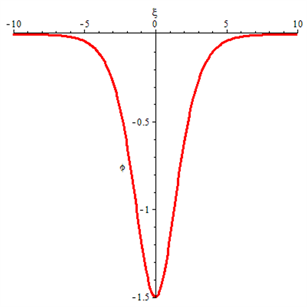
Figure 10. The solitary solution of Eq. (16)
图10. 孤立波解式(16)
(2) 当 时,定义的是系统(5)围绕中心平衡点 一簇周期轨线,对应于系统(5)的一簇周期闭轨。计算可得其精确解如下:
(17)
其中 是方程 的解,且满足 。
(iv) 。平衡点 是鞍点,平衡点 是中心。过鞍点 的同宿轨表达式为式(16),对应于系统(5)的孤立波解。系统(5)围绕中心平衡点的一簇周期轨对应的周期波解为式(12),且 。
3. 结论
应用发展的动力系统分支方法,本文得到了(1 + 1)-维Benjiamin Ono方程在不同参数条件下所有行波解的精确表达式,文中由式(9),(12),(13),(16),(17)分别给出,由这些公式可见,方程(3)存在孤立波解、周期波解。
基金项目
江西省教育厅高等学校教学改革研究课题(JXJG-19-42-1)资助。
文章引用
杨德牛. (1 + 1)-维Benjiamin Ono方程的行波解及分岔
Bifurcation and Travelling Wave Solutions for the (1 + 1)-Dimensional Benjiamin Ono Equation[J]. 应用数学进展, 2022, 11(11): 7503-7511. https://doi.org/10.12677/AAM.2022.1111795
参考文献
- 1. McCue Scott, W., El Hachem, M. and Simpson, M.J. (2021) Exact Sharp-Fronted Travelling Wave Solutions of the Fisher-KPP Equation. Applied Mathematics Letters, 114, Article ID: 106918. https://doi.org/10.1016/j.aml.2020.106918
- 2. 朱佐农. Fisher方程的新的显式精确孤波解[J]. 数学的实践与认识, 1995(2): 70-73.
- 3. Yang, G.X. (2013) Hopf Bifurcation of Traveling Wave Solutions of Delayed Fisher-KPP Equation. Applied Mathematics and Computation, 220, 213-220. https://doi.org/10.1016/j.amc.2013.06.051
- 4. Matinfar, M. and Ghanbari, M. (2009) The Application of the Modified Variational Iteration Method on the Generalized Fisher’s Equation. Journal of Applied Mathematics and Com-puting, 31, 165-175. https://doi.org/10.1007/s12190-008-0199-0
- 5. 张强, 曾艳, 周艳红. 一类广义Fisher方程的稳定性和动态分歧[J]. 四川大学学报(自然科学版), 2019, 56(2): 222-226.
- 6. Kametaka, Y. (1976) On the Nonlinear Diffusion Equation of Kolmogorov-Petrovskii-Piskunov Type. Osaka Journal of Mathematics, 13, 11-66.
- 7. Rodrigo, M. and Mimura, M. (2002) Annihilation Dynamics in the KPP-Fisher Equation. European Journal of Applied Mathematics, 13, 195-204. https://doi.org/10.1017/S0956792501004764
- 8. Hamel, F. and Roques, L. (2010) Fast Propagation for KPP Equations with Slowly Decaying Initial Conditions. Journal of Differential Equations, 249, 1726-1745. https://doi.org/10.1016/j.jde.2010.06.025
- 9. Moet, H.J.K. (2006) A Note on the Asymptotic Behavior of Solu-tions of the KPP Equation. SIAM Journal on Mathematical Analysis, 10, 728-732. https://doi.org/10.1137/0510067
- 10. Temam, R. (1997) Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer, New York. https://doi.org/10.1007/978-1-4612-0645-3
- 11. 杨娟, 冯庆江, 曾春花. 一类非线性数学物理方程的精确解[J]. 数学的实践与认识, 2018, 48(17): 309-313.
- 12. 许瑞麟, 许晓革, 孟祥花. (1+1)维Benjiamin Ono方程的精确显式解[J]. 北京信息科技大学学报(自然科学版), 2011, 26(3): 58-61.
- 13. 陈立, 何姝琦, 董亚莹. Benny-Luke方程和Phi-4方程的精确行波解[J]. 纯粹数学与应用数学, 2015, 31(6): 604-610.
- 14. 李继彬. 非线性非齐次弹性材料模型的精确模态波解和动力学性质[J]. 中国科学:数学, 2017, 47(1): 147-154.
- 15. 李继彬. 两类Boussinesq方程的行波解分支[J]. 中国科学: 数学, 2008, 38(11): 1221-1234.