International Journal of Mechanics Research
Vol.07 No.02(2018), Article ID:25451,8
pages
10.12677/IJM.2018.72005
Layer-Model-Based Three-Dimensional Interface Crack Analysis
Shuo Wang, Zheng Zhang
Institute of Solid Mechanics, Beihang University, Beijing

Received: May 28th, 2018; accepted: Jun. 8th, 2018; published: Jun. 15th, 2018

ABSTRACT
In the field of engineering, interface problems exist extensively, and the special nature of the interface leads to the destruction of bonded materials that often begins at this location. Therefore, in order to ensure the safety of the entire material, the interface crack must be studied. Different from the homogeneous material cracks, the interface cracks show some special properties, such as the oscillation singularity of the field stress at the crack tip, and the dimension of the stress intensity factor. Numerous scholars also proposed a new theory to improve the existing deficiencies. Considering the special properties of interfacial cracks, according to the interface layer theory, the interface of bonded materials is regarded as a functionally graded material (FGM) layer with thickness, and a theoretical system of fracture mechanics for the elliptic cracks in the interfacial layer is established for analysis, which provides a theoretical method for the study of three-dimensional interface crack failure mechanism.
Keywords:Interface Cracks, Functionally Graded Materials, Three-Dimensional Fracture Theory
基于界面层模型的三维界面裂纹分析
王硕,张铮
北京航空航天大学,固体力学研究所,北京

收稿日期:2018年5月28日;录用日期:2018年6月8日;发布日期:2018年6月15日

摘 要
在工程领域中,界面问题广泛存在,界面的特殊性质导致结合材料的破坏往往始于该处,所以为了保证整个材料的使用安全必须对界面裂纹进行研究。与均质材料裂纹不同,界面裂纹表现出了一些特殊的性质,如裂纹尖端场应力的振荡奇异性、应力强度因子的量纲等问题,不少学者也提出了改进原有不足的新理论。考虑到界面裂纹具有的某些特殊性质,本文依据界面层理论,将结合材料的界面视为具有厚度的功能梯度材料(FGM)层,并建立针对界面层内椭圆裂纹的断裂力学理论体系进行分析,对三维界面裂纹破坏机理的研究提供了理论方法。
关键词 :界面裂纹,功能梯度材料,三维断裂理论

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着各种新型功能性材料的日益发展,工程领域中对于轻质、强度、刚度的要求也逐渐提高。在这些新型材料中,我们把两种不同的材料利用粘接、焊接等技术连接在一起所使用的结构称为结合材料。界面问题在结合材料中广泛存在,因此对于结合材料界面的力学性能研究也需要更加深入 [1] 。目前关于均质材料裂纹的研究已经趋于成熟 [2] ,但是如果将经典的裂纹模型引入界面问题中会出现两种特殊现象:界面的应力奇异性和界面裂纹尖端的应力振荡奇异性,因此许多学者从不同的角度出发提出了改进模型,顺利地解决经典模型存在的问题,比较经典的有Comninou的接触区理论、Erdoga的界面层理论以及Rice的小范围屈服理论 [3] ,已经被广泛接受。
界面层理论的最大优势就在于,符合物理常识并且能够消除界面裂纹的应力振荡奇异性,该理论认为,结合材料的界面是实际存在的非均匀各向同性材料,其厚度均匀并且很薄,弹性模量沿厚度连续变化,与功能梯度材料(FGM)的性质契合 [4] [5] 。虽然到目前为止关于界面的研究很多,但主要还是以平面应力和平面应变问题为研究对象 [6] [7] [8] ,对于一般性的三维问题,相关的研究还远远不足。本文将界面层理论扩展至三维问题,建立基于功能梯度材料的三维模型并建立相应的理论分析体系。
2. 界面层理论
Williams [2] 利用均质材料裂纹的理论解,对界面裂纹尖端场进行研究,由于界面两侧材料性质不同,发现直接应用断裂力学的理论模型存在振荡奇异性等不合理的情况,即在理论上裂纹尖端上下表面互相嵌入,如图1所示,这显然不符合物理常识。
据此,Erdogan认为界面应当是具有细观结构的界面层,无厚度的理想界面不能够体现出界面的性质。经过实验测量与分析,他提出界面层是厚度一致的非均匀各向同性材料,其弹性模量沿厚度连续变化,而泊松比则可以视为常数,模型如图2所示,结合材料中①区域和②区域的弹性模量为常数,而在两区域之间材料属性随着纵坐标的变化而变化,这里,E(y)表示界面层的弹性模量。这样的模型与均质材料裂纹模型相似,有效地消除了应力振荡的现象。
3. 三维界面裂纹模型
与均质材料裂纹不同的是,即使远场仅受单向应力作用,界面裂纹仍然处于I、II、III型复合的状态。至于一般三维界面裂纹,其应力状态可能会表现得更加复杂。因此,考虑到界面裂纹的多型耦合现象,

Figure 1. Oscillation singularity of interfacial crack stress field
图1. 界面裂纹应力场的振荡奇异性

Figure 2. Diagram of interface layer model [4]
图2. 界面层模型示意图 [4]
依据界面层理论的相关内容,本文将现有的界面层理论推广到三维界面层裂纹(如图3所示)。
实际中常见的三维裂纹可大致认为是椭圆形。设在无限大材料中有一椭圆形深埋片状裂纹(位于界面层内),基于该椭圆裂纹的中心建立坐标系(参看图3),其方程为
(1)
椭圆边界上的点可以用参数方程表示为(如图4所示)
(2)
为得到较简单的平衡方程并对裂纹及其邻域进行描述,过边界上一点P0 (参看图4左图)建立局部坐标系P0tny (参看图4右图),P0点为局部坐标原点,P0n为P0点在裂纹扩展平面内的法线,与Ox轴(即椭圆长轴)夹角为φ,P0t为P0点在裂纹扩展平面内的切线;在P0点的法平面nP0y (即垂直于切线P0t的平
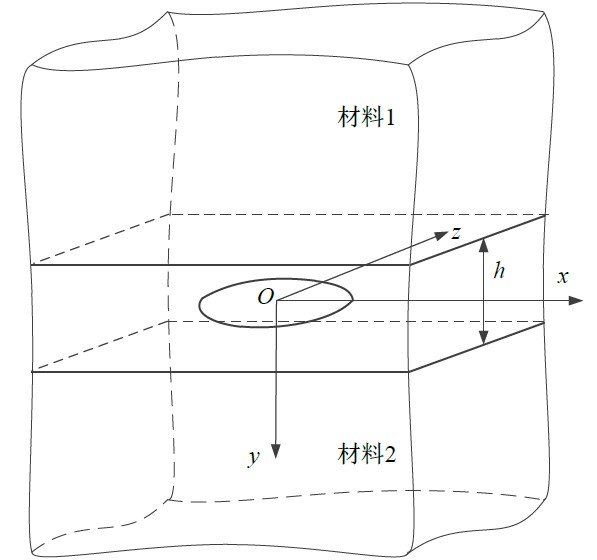
Figure 3. Diagram of three-dimensional interface layer model
图3. 三维界面层模型图
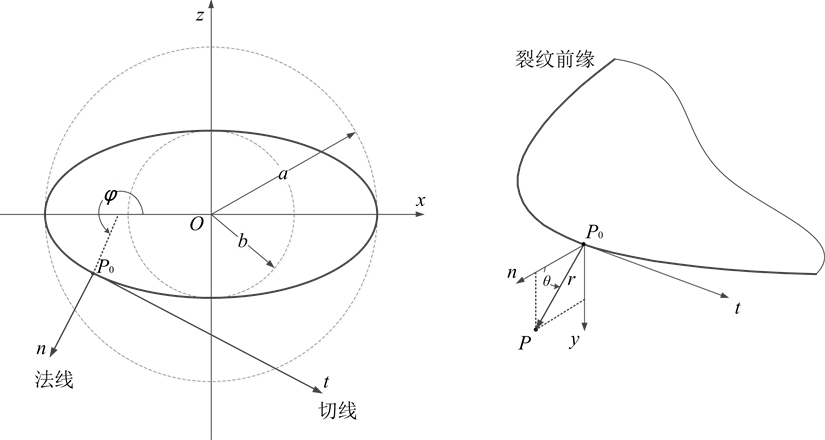
Figure 4. Coordinate system in three-dimensional model
图4. 三维模型的坐标系
面)内引入极坐标系(r, θ),即rP0θ为过P0点的法平面上的极坐标系(这里,y轴垂直于P0点的切线P0t和法线P0n)。
于是,可以利用上述平面坐标系与参数φ (即坐标系(φ, r, θ))来描述空间内任一点,其中,整体坐标系与局部坐标系的变换关系为
,其中 为椭圆离心率。 (3)
4. 求解三维界面裂纹问题
由于裂纹前缘常常呈现曲线扩展状态,因此断裂问题并不适合采用直角坐标系进行描述。本文以二维裂纹分析为基础,建立上述法平面内的极坐标加上切线坐标的局部坐标系,如图5所示,进一步按照三维弹性力学理论 [9] ,在前文中裂纹前缘处建立的全局坐标系中,推导建立三维裂纹分析的理论体系。
4.1. 三维界面裂纹的弹性理论方程
如上所述,在曲线裂纹前缘的每一点,本文建立相应的局部柱坐标系,用于描述裂纹前缘的力学分析体系,进而建立各种力学基本方程。
首先,结合柱坐标系下的平衡方程,可得到该局部坐标系下的平衡方程(无体力):
 (4)
(4)
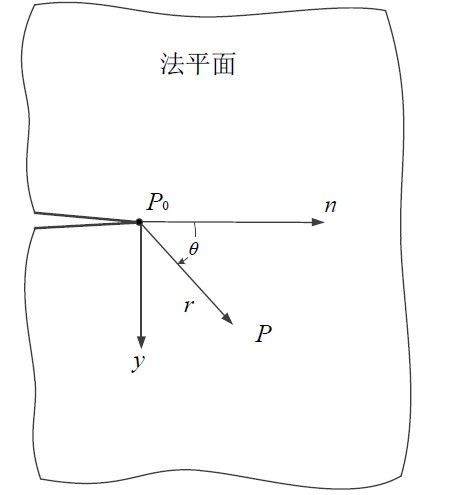
Figure 5. Local coordinate system in the front of crack
图5. 裂纹前缘局部坐标系
其中
同理,几何方程为
(5)
物理方程为
(6)
其中
体应变 ,
剪切模量 ,
拉梅参数 。
值得注意的是,界面层模型中的λ和G并非常数,而是与界面层厚度坐标y有关的函数:
(7)
最后,裂纹面的边界条件为
(8)
4.2. 平衡方程的简化
上述方程实际上的求解相当困难,考虑对其进行简化,考虑到实际情况下界面层厚度很薄,假设弹性模量沿界面层厚度方向呈线性变化,而泊松比为常数,则剪切模量的表达式可记为
(9)
由于弹性模量沿界面层厚度方向变化,所以当将其引入裂纹前缘的柱坐标系中会造成耦合现象,给求解带来不便。在求解时可采用无裂纹材料远场应力加上含裂纹体简化后裂尖场应力,即分别简化的方式处理。
4.2.1. 远场应力的简化计算
界面层模型如图3所示,进行远场应力分析时忽略裂纹前缘场的作用,假设界面层内位移场沿界面层厚度线性分布,直角坐标系下平衡方程进一步简化为
(10)
其中w为仅与x,z坐标相关的函数, 为xOz平面上各点的位移量。此时满足对于给定的(x, z)坐标则有:
(三者均与y坐标无关) (11)
将式(11)代入直角坐标系下的几何方程和物理方程,可将平衡方程进一步表示为
(12)
4.2.2. 裂尖应力场计算
在传统断裂力学中,裂纹前缘应力场(平面问题)具有 的奇异性 [9] 。在界面断裂问题中,问题的物理性质并没有改变,裂纹的界面特征是组成结合材料的两种介质不同造成的,因此本文仍假设裂纹前缘应力场形式为
(13)
其中a,b为椭圆裂纹的半轴长,其中n < 0代表应力具有奇异性。
此时原平衡方程(4)可被简化为:
(14)
上式中n的取值可根据平衡方程的推导计算结果确定,值得注意的是,若n = −1/2则可说明三维应力场的形式为
(15)
这将表明三维界面裂纹和平面问题中的应力场具有同阶的应力奇异性,也意味着平面问题中应力强度因子的定义同样适用于三维问题。
5. 总结
结合材料的界面断裂研究已经比较深入,但存在的问题仍然较多。界面断裂问题的复杂性,一是来自结合材料不同介质的材料性质不同,一是来自裂纹尖端场的奇异性,一是来自裂纹扩展的三维性,即裂纹前缘呈现曲线型扩展。传统断裂力学中裂纹问题主要是以平面问题为研究对象,在简单载荷作用下,裂纹扩展型式与载荷作用相一致,因此,裂纹前缘呈直线型平行推展。而对于结合材料的界面,由于界面两侧材质不同,即使在简单载荷下,裂纹尖端应力场也变得非常复杂,裂纹扩展呈现三种裂纹型式耦合的特征,这是造成裂纹前缘呈现曲线型扩展的重要驱动力。
因此,建立结合材料界面裂纹分析的三维理论方法,对分析界面裂纹扩展趋势,确定界面裂纹强度,为结构设计提供设计方法和强度校核标准,都具有重要意义。
本文力图建立三维界面裂纹分析的断裂力学方法:针对界面裂纹,建立适于理论描述的曲线坐标系,包括全局坐标系和局部坐标系;根据界面的构成特点,建立界面层模型,并假设其材料参数沿厚度方向线性分布;以三维弹性力学理论为基础,在裂纹前缘建立平衡方程,结合几何关系、物理关系以及边界条件,得到具有曲线前缘的界面裂纹的理论分析方法。
由此可见,上述方法不仅具有理论的严谨性,更兼具问题的适用性,对曲线前缘的界面裂纹分析,具有极强的针对性。本文还进一步引入了界面层位移场的线性简化和裂纹尖端应力场平方根奇异性,对理论分析体系进行了简化。本文模型满足界面裂纹的基本特征,对界面裂纹问题具备物理的适用性,可以作为理论分析的基础和方法,也是工程应用的理论工具。
文章引用
王 硕,张 铮. 基于界面层模型的三维界面裂纹分析
Layer-Model-Based Three-Dimensional Interface Crack Analysis[J]. 力学研究, 2018, 07(02): 36-43. https://doi.org/10.12677/IJM.2018.72005
参考文献
- 1. 于慧子. 二维界面端应力奇异性及界面裂纹分析[D]: [硕士学位论文]. 沈阳: 东北大学, 2014.
- 2. 嵇醒. 断裂力学判据的评述[J]. 力学学报, 2016, 48(4): 741-753.
- 3. 许金泉. 界面力学[M]. 北京: 科学出版社, 2006.
- 4. Gupta, A. and Talha, M. (2015) Recent Development in Modeling and Analysis of Functionally Graded Materials and Structures. Progress in Aerospace Sciences, 79, 1-14. https://doi.org/10.1016/j.paerosci.2015.07.001
- 5. Zhong, Z., Wu, L.Z. and Chen, W.Q. (2010) Progress in the Study on Mechanics Problems of Functionally Graded Materials and Structures. Advances in Mechanics, 40, 528-541.
- 6. 黄干云, 汪越胜, 余寿文. 功能梯度材料的平面断裂力学分析[J]. 力学学报, 2005, 37(1): 1-8.
- 7. Ji, X. (2016) SIF-Based Fracture Criterion for Interface Cracks. Acta Mechanica Sinica, 32, 491-496. https://doi.org/10.1007/s10409-015-0551-1
- 8. 邸克, 杨月诚. 功能梯度界面层模型断裂问题研究进展[J]. 兵器装备工程学报, 2012, 33(10): 116-119.
- 9. 匡震邦, 马法尚. 裂纹端部场[M]. 西安: 西安交通大学出版社, 2002.