International Journal of Mechanics Research
Vol.
08
No.
03
(
2019
), Article ID:
32084
,
10
pages
10.12677/IJM.2019.83021
The Stability and Soliton of the Optimal Velocity Model Considering Speed Limit
Guangzhu He, Cuncai Hua
School of Mathematics, Yunnan Normal University, Kunming Yunnan
Received: Aug. 19th, 2019; accepted: Sep. 2nd, 2019; published: Sep. 9th, 2019

ABSTRACT
Based on the optimal velocity model, this paper designs a traffic flow model which takes into account the driver’s advance time to know the speed limit information. By using the linear stability analysis method, the stability condition of the model is obtained. It shows that the influence of the speed limit makes the stable region of traffic flow expand obviously. The density wave equations such as Burgers equation, KdV equation and mKdV equation are derived respectively from the reduced perturbation method in the stable region, metastable region and unstable region. The phenomena of traffic congestion under the speed limit are described by the solitary wave solution of Burgers and KdV equation, and by the kink-antikink solution of mKdV equation.
Keywords:The Optimal Velocity Model, Speed Limit, Stability, Density Wave
考虑限速的最优速度模型的稳定性与孤波
和光珠,化存才
云南师范大学数学学院,云南 昆明
收稿日期:2019年8月19日;录用日期:2019年9月2日;发布日期:2019年9月9日

摘 要
本文基于最优速度模型,设计了考虑驾驶员提前时间获知限速信息的交通流模型。利用线性稳定性分析方法,得到了模型的稳定性条件。表明限速信息的影响使得交通流的稳定区域有明显扩大。利用约化摄动法对模型进行分析,分别在稳定区域、亚稳态区域和不稳定区域导出密度波方程——Burgers方程、KdV方程和mKdV方程。通过Burgers方程、KdV方程的孤波解以及mKdV方程的扭结–反扭结波解描述了提前获知限速信息下的交通流堵塞现象。
关键词 :最优速度模型,限速,稳定性,密度波

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
许多年来,随着社会经济的快速发展,城市化建设的进程加快,人们生活质量水平的显著提升,城市交通需求高速增长,道路车辆骤增,产生了交通拥堵、交通事故、交通污染和能源消耗等四大城市交通问题。其中,交通拥堵问题是基础,一直备受关注。交通拥堵是交通流复杂性的一个重要特征,被认为是由于车辆之间相互作用而引起的密度波传播的极限情形 [1] 。为研究交通流的复杂性问题,学者们相继提出了许多跟驰模型 [2] - [7] 来数学地描述和解释交通流中的复杂现象。
交通流模型按聚集水平可分为宏观模型、中观模型和微观模型。具有最优速度函数的车辆跟驰模型是微观交通流模型的重要代表,并通过仿真分析技术得到了广泛的研究。最早的跟驰模型是由Pipes [8] 于1953年提出。1995年,Bando [9] 等基于驾驶员根据车头时距调整车速的思想,首次提出了最优速度模型(OVM),该模型解决了无限加速问题。1998年,Helbing [10] 等利用经验数据对OVM进行验证,提出了一种广义力模型(GFM),它克服了OVM存在减速不现实、加速度过大的问题。2001年,Jiang [11] 等发现GFM在高密度下表现出较差的汽车运动延迟时间和运动波速,并提出了考虑正负速度差对跟驰模型的影响的全速度差模型(FVDM)。
当今,智能交通系统(Intelligent Transport System,简称ITS),是道路交通和运输科技发展的前沿。它的快速发展和应用正通过提供智能交通信息改变着我们的交通控制和管理方式,成为人们应对严重交通拥堵的解决方案。在此背景下,跟驰模型也得到了新的扩展。例如,文献 [12] [13] [14] 在考虑各种交通因素和信息的基础上,提出了许多新的OVM和FVDM跟驰模型。这些模型主要考虑协同控制驾驶的范畴,即:车辆在运行过程中,根据当前或历史时刻的其他车辆的位置信息或运动状态来调整自身的行驶状态,而每辆车的运动方程都由被考虑车辆本身和其他车辆的交通信息组成,从而通过协同驾驶控制达到抑制交通拥堵、提高交通流稳定性的目的。然而,由于存在众多因素,协同控制驾驶在实践中实施还存在一定的困难。首先,需要获取其他车辆的准确可靠的交通信息;其次,在车与车之间要互联通信,协同控制的实施效果在很大程度上取决于通讯网络的质量,在实时传输数据时,无线局域网也会存在传输的延迟,已有相关文献证明这对交通流的稳定性会产生负面影响 [15] [16] [17] [18] 。最后,在车道上,任何车辆可以在任何时候从道路的任何位置驶入或是离开,这可能会使得车辆之间会突然发生变化,这些传输的错误信息可能导致驾驶员做出错误的操作。
针对上述问题,有学者考虑不需要与其他车辆协同驾驶,仅通过每一辆车的自稳定控制来稳定交通流,2015年,Li [19] 等首次在OVM中加入当前与历史速度的速度差,考虑历史速度对稳定性的影响,提出了一种交通动态的微分差分方程,通过理论分析和数值模拟验证了自稳定效应。2017年,Chen [20] 等考虑到驾驶员对自身车速变化的连续记忆效应,改进了自稳定控制驾驶行为的跟驰模型,结果表明驾驶员的连续记忆效应能提高车流的稳定性,有效抑制交通流的堵塞。2018年,Sun [21] 等将车头时距自稳定控制因子加入到OVM中,给出了一种扩展的自稳定最优速度模型,该模型结果表明自稳定驾驶行为对交通流的稳定性和流量起着积极有效的作用。可见,根据车辆自身的速度或位置信息来调整当前时刻的运动状态,以达到稳定交通流的相关研究得到了进一步发展。然而,到目前为止,关于自稳定控制方面存在的研究工作还很少。毋庸置疑,车辆的协同控制会对驾驶行为产生影响,而限速信息也会对驾驶行为产生一定的影响。在行驶过程中,驾驶员必须注意前后车辆,也要提前预知前方的交通状况,以避免任何潜在的冲突。在行驶车道上,交通流会受到速度的影响,而驾驶员也会随不同交通状况控制速度。如果能提前获知限速信息,驾驶员可以提前做好相应速度的调整,以保证车辆的安全驾驶,从而更好地避免交通拥堵的发生。
本文将从经典的最优速度模型(OVM)出发,主要考虑驾驶员提前 时间获知限速信息带来的影响,例如:智能车载导航系统提前提示前方路况和限速信息;在高速公路上,路边的限速标示牌提示等,都属于提前时间提示限速信息。通过引入限速信息来更好地描述真实的交通环境,使得改进的OVM模型更加符合实际交通流,进而可以有效地解释一些复杂的交通现象。为此,本文给出了新的扩展的最优速度模型,通过线性稳定性分析方法导出模型的稳定性条件,通过约化摄动方法导出三个不同区域内的密度波方程,从而分析限速对驾驶行为的影响,为破解城市交通拥堵问题提供理论依据。
2. 模型的提出
跟驰模型是在微观交通模型的基础上对车辆的运动方程等微观交通动力学问题进行描述。
1995年,Bando等 [9] 提出的最优速度模型很好地描述了交通流的一些非线性现象,其运动方程如下:
(1)
其中,a表示驾驶员的敏感系数, (单位:m), (单位:m/s)分别表示第n辆车在t (单位:s)时刻的位置和速度, 表示第 辆车(即前向车辆)与第n辆车(即跟驰车辆)之间的车头间距,模型的基本思想是:第n辆车在t时刻的加速度 (单位:m/s2)由实际速度 与最优速度 (单位:m/s)之差决定,它依赖于前一辆车的车头时距,取如下形式的双曲正切函数:
(2)
其中,取 (单位:m)为安全距离, (单位:m/s)为最大速度。可知最优速度函数是一个
单调递增函数,因为 为 的一阶导数,并且无论 的
值如何,都是非负的。由 可知系式(2)具有上限。
2015年,Lie等 [19] 通过调整车辆自身的速度差(当前速度与历史速度)达到稳定交通流的目的,提出了如下自稳定控制驾驶的跟驰模型:
(3)
其中, 是当前时间t与历史时间 之差, 表示考虑当前速度与历史速度之差的敏感系数, 表示车辆n当前速度 与历史速度 的速度差。
2017年,Chen等 [20] 考虑驾驶员对自身车速变化的连续记忆效应,将模型(2)拓展为具有连续记忆效应的如下交通流跟驰模型:
(4)
其中, 表示考虑连续记忆效应的敏感系数。采用积分形式,该模型可描述驾驶员在 时间内
的连续记忆效应,并能真实地刻画车辆连续运动的过程。由积分中值定理可知, ,
其中 ,, 为记忆参数, 越大,驾驶员的记忆时间越长,则记忆效应越强。
2018年,Sun等 [21] 将车头时距自稳控制因子加入OVM中,提出如下扩展的自稳定最优速度模型:
(5)
其中,h表示稳态稳定车头时距, 表示自稳定控制效果, 是车头时距自稳定控制行为响应系数。
从交通管理的角度来看,最重要的问题是抑制交通堵塞。为提高城市交通稳定性,保障交通安全畅通,限制车速是一项重要的措施。关于限速信息,一方面,可以通过车辆GPS导航系统来获知;另一方面,又可以通过道路的限速标示来获知。为此,本文在经典最优速度模型的基础上,考虑驾驶员提前 时间获知限速信息,给出如下交通流模型:
(6)
其中,a表示驾驶员的敏感系数, 表示驾驶员提前 时间预知本车速度与当前速度之差,我们期望速度差项 可以通过抑制交通堵塞来影响交通流稳定性, 表示有提前获知限速信息下的敏感系数。由(6)式可知, 项与其他车辆的交通信息无关,它完全依赖于被考虑车辆的交通数据,而这可以通过车辆上的GPS导航系统获得。如果驾驶员提前 时间预知本车速度与当前速度之间的速度差能够稳定交通系统,则意味着我们可以通过自稳定来控制每辆车,进而改善交通的稳定性。
为方便后面的计算,将模型(6)改写为如下形式:
(7)
3. 模型(7)的稳定性分析
本节中,我们采用线性稳定性方法分析导出模型(7)的稳定性条件。
首先,假设初始状态为稳定态,车辆的车头间距均为h,对应的优化速度为 。此时,稳态交通流的车辆位置可表示为:
(8)
其中:N是车辆总数,L是道路长度(单位:m)。若在t时刻给稳态交通系统施加一个小扰动 ,使得车流运行产生偏离,则 表示为:
(9)
为扰动影响下车辆的实际位移。
其次,将(8)和(9)式代入方程(7),整理得到:
(10)
其中, ,将(9)式泰勒展开,有:
(11)
式中 为最优速度函数 在 处的导数。再将 代入(11),整理得到关于扰动 的如下式子:
(12)
最后,将参数z展开为 代入(12)。比较 的相同次幂,得到z表达式中一阶项和二阶项的系数如下:
, (13)
如果 为负,则初始均匀的稳定流将变得不稳定;如果 为正,则将保持原有的稳定流状态不变。由此得到(7)在考虑驾驶员提前 时间获取限速信息的临界条件为:
(14)
于是,当 时,交通流将处于稳定状态。即当驾驶员获取限速信息的提前时间 变小时,敏感系数 将增大,意味着驾驶员驾驶行为加强,交通流更加稳定。相反,当 变小时,a也变大,并且a的变化幅度大于 的变化幅度,这表明a是主敏感系数。当 时,稳定性条件变为OVM的稳定性条件,即: 。
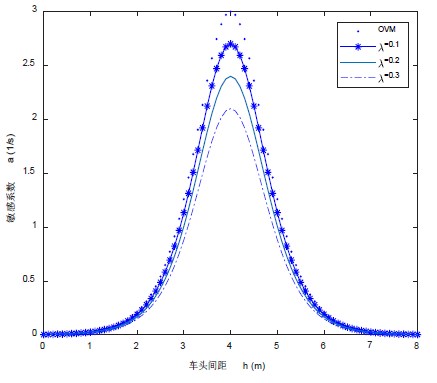
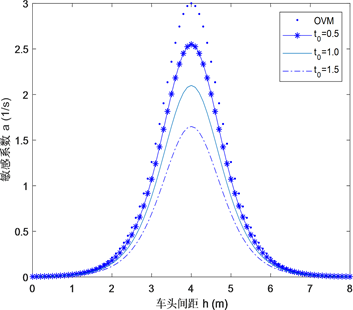
图1给出了(14)在不同 和 组合下的临界稳定曲线。图1(a)为 时,不同 下的中性稳定曲线。中性稳定曲线上方为稳定区域,表示无交通拥堵的自由相;中性曲线下方区域为不稳定区域,表示随着走走停停的密度波向后演化的交通堵塞相,每条曲线的峰值代表临界点。从图1(a)可看出,随着对限速产生的敏感参数 的增大,稳定区域也增大,表明驾驶员提前 时间获取限速信息能有效增强车流的稳定性。图1(b)为模型(7)在固定 ,不同时间 下的中性稳定曲线。从图1(b)可看出,随着提前获取限速信息时间 的增大,稳定区域也增大,表明驾驶员越早获取限速信息,就能越早调整车速,使车流稳定,避免交通拥堵的发生。
 (a)
(a)
 (b)
(b)
Figure 1. The neutral stability lines in the headway-sensitivity space for different parameter combinations. (a) , (b)
图1. 不同参数组合下的车头时距与敏感系数之间的临界稳定曲线。(a) , (b)
4. 模型(7)的约化摄动分析和孤立波
交通堵塞其实质就是交通流模型的孤立波现象。根据前面第3节的稳定性条件,交通流区域可以分为:稳定区域、不稳定区域和亚稳态区域。在三种不同的区域可以用约化摄动法导出各自的非线性波方程,从而给出相应的交通流密度波。
为后面的计算方便,我们将模型(7)改写为
(15)
4.1. 在稳定流区域导出Burgers方程
在稳定流区域,满足线性稳定性条件 。
对于空间变量n和时间变量t,我们定义慢变量X和T:
, (16)
这里 且b是一个待确定的常数。设车头时距为:
(17)
将式(16)和(17)代入(15),泰勒展开至 量级,得到如下非线性偏微分方程:
(18)
其中, ,,
,,。
令 ,消去 的二次项后,将(18)简化为:
(19)
因此,在稳定性条件下,在稳定区域可得到
(20)
此时,(19)是一个Burgers方程,它有一个解为:
(21)
其中, , 表示沿着x轴的斜率, 表示激波波前的坐标。
恰好为三角激波的传播速度。三角激波相对运动车辆向后传播,随着平均车间距的增加,传播速度减小。从 可看出,当 时, 的极限值为经典的OVM,即没有考虑驾驶员提前 时间获知限速信息,结果为OVM的极限状态。
4.2. 在不稳定区域导出mKdV方程
在不稳定区域内,研究(15)在临界点 ( 为临界敏感度, 为临界车头间距)附近空间变量n和时间变量t的慢变行为,我们定义慢变量X和T:
,, (22)
设车头时距为:
(23)
将式(22)和(23)代入(15),泰勒展开至 量级,得到如下非线性偏微分方程:
(24)
令 ,,和 。在临界点 附近,忽略 和 量级,方程(24)可简化为:
(25)
其中, ,,,
,
对(25)作如下变换:
, (26)
得到含有 校正项的mKdV方程:
(27)
其中,
(28)
忽略(27)中的校正项 ,(27)就是mKdV方程,它的扭结—反扭结波解为:
(29)
为了得到方程(27)的传播速度c, 必须满足可解性条件:
(30)
其中c为解的传播速度。通过求解下面的积分方程可得到扭结—反扭结波的传播速度c为:
(31)
用Zhang G [22] 等人的方法来求解方程(31),可得到c的表达式为
(32)
因此,车头间距的扭结—反扭结波的解为:
(33)
扭结–反扭结密度波的振幅A为:
,其中, (34)
扭结–反扭结解代表共存相,包括低密度的自由运动相和高密度的拥挤相,自由运动相和拥挤相的车头时距分别由 和 给出。从扭结波的振幅(34)中可看出,提前时间 越大,振幅A越小,即考虑驾驶员获取限速信息的提前时间越早,交通堵塞现象越弱。
4.3. 在亚稳态区域导出KdV方程
现在分析方程(15)在中性稳定线 附近亚稳定区域内的交通流性态。对于空间变量n和时间变量t,我们仍然定义慢变量X和T:
,, (35)
这里 且b是一个待确定的常数。设车头时距为:
(36)
将(35)和(36)代入(15),泰勒展开到 量级,并令 ,,和 ,我们有
(37)
其中, ,,,
,。
对(37)作如下变换:
,,, (38)
得到含有校正项 的KdV方程:
(39)
忽略(39)中的 项,得到标准的KdV方程,其孤立波解为:
(40)
其中,振幅A的取值将在下面给出。假设 ,考虑(39)中的 项,可以在孤立波解系中确定式(39)的唯一解。由文献 [23] 得振幅满足的可解性条件为:
(41)
积分后,得到孤立波的振幅A为:
(42)
故(39)的解变为:
(43)
替换回原有变量,从而求得由孤立波表示的车头间距为:
(44)
孤立波形式的密度波解刻画了交通流的拥堵。如果孤立波的振幅越小,那么交通堵塞就越严重。从(44)分析发现:当 变大时,车头间距 变大,交通就会越通畅,进而减少交通拥堵的发生。
5. 结论
本文考虑驾驶员提前 时间获知限速信息,在经典最优速度模型的基础上给出了一种扩展的最优速度模型(6)。
利用线性稳定性方法,得到模型(6)的线性稳定判据,表明驾驶员提前 时间获知限速信息的影响使得交通流的稳定区域明显扩大。
利用约化摄动法,分别导出了在稳定区域、亚稳态区域和不稳定区域中的交通密度波方程,即Burgers方程、KdV方程和mKdV方程。通过它们的孤波解和扭结波解分析得出,随着驾驶员提前获知限速信息的时间 越长,交通流稳定区域增大,表明拥堵现象会得到很大的缓解,从而更能确保交通安全畅通。
致谢
感谢审稿人和编辑部提供的有益建议。
基金项目
国家自然科学基金项目(批准号:11162020)资助的课题。
文章引用
和光珠,化存才. 考虑限速的最优速度模型的稳定性与孤波
The Stability and Soliton of the Optimal Velocity Model Considering Speed Limit[J]. 力学研究, 2019, 08(03): 187-196. https://doi.org/10.12677/IJM.2019.83021
参考文献
- 1. 袁娜, 化存才. 多前车速度差的车辆跟驰模型的稳定性与孤波[J]. 物理学报, 2012, 61(16): 108-114.
- 2. 杨龙海, 赵顺, 徐洪. 基于改进优化速度函数的跟驰模型研究[J]. 交通运输系统工程与信息, 2017, 17(2): 41-46.
- 3. Shi, Y.F. and Yang, L. (2017) Improved Coupled Map Car-Following Model Considering Partial Car-to-Car Communication and Its Jam Analysis. Canadian Journal of Physics, 95, 1096-1102. https://doi.org/10.1139/cjp-2016-0639
- 4. 王威, 吴中. 考虑多车间距的跟驰模型及混合交通流的数值模拟[J]. 华东交通大学学报, 2018(6): 72-80.
- 5. 秦严严, 王昊, 冉斌. 考虑多前车反馈的智能网联车辆跟驰模型[J]. 交通运输系统工程与信息, 2018, 18(3): 48-54.
- 6. Gopal, K.K., Krishna, J. and Gaurav, R. (2019) Stability, Convergence and Hopf Bifurcation Analyses of the Classical Car-Following Model. Nonlinear Dynamic, 96, 185-204. https://doi.org/10.1007/s11071-019-04783-3
- 7. 李宏刚, 高哈尔∙达吾力, 王帅, 等. 考虑临近车道行人对交通流影响的改进跟驰模型[J]. 北京航空航天大学学报, 2019, 45(2): 422-428.
- 8. Louis, A. Pipes. (1953) An Operational Analysis of Traffic Dynamics. Journal of Applied Physics, 274, 274-281. https://doi.org/10.1063/1.1721265
- 9. Bando, M. and Hasebe, K. (1995) Dynamical Model of Traffic Congestion and Numerical Simulation. Physical Review E, 51, 1035-1042. https://doi.org/10.1103/PhysRevE.51.1035
- 10. Helbing, D. and Tilch, B. (1998) Generalized Force Model of Traffic Dynamics. Physical Review E, 58, 133-138. https://doi.org/10.1103/PhysRevE.58.133
- 11. Jiang, R., Wu, Q.L. and Zhu, Z.J. (2001) Full Velocity Difference Model for a Car-Following Theory. Physical Review E, 64, Article ID: 017101. https://doi.org/10.1103/PhysRevE.64.017101
- 12. Zheng, L.J, Tian, C., Sun, D.H. and Liu, N.L. (2012) A New Car-Following Model with Consideration of Anticipation Driving Behavior. Nonlinear Dynamic, 70, 1205-1211. https://doi.org/10.1007/s11071-012-0524-x
- 13. Peng, G.H. and Cheng, R.J. (2013) A New Car-Following Model with the Consid-eration of Anticipation Optimal Velocity. Physica A, 392, 3563-3569.
- 14. Tang, T.Q., Huang, H.J. and Shang, H.Y. (2015) Influ-ences of the Driver’s Bounded Rationality on Micro Driving Behavior, Fuel Consumption and Emissions. Transportation Research Part D, 41, 423-432.
- 15. Zhu, H.B. and Dai, S.Q. (2008) Analysis of Car-Following Model Considering Driver’s Physical Delay in Sensing Headway. Physica A, 387, 3290-3298.
- 16. Kang, Y.R. and Sun, D.H. (2013) Lattice Hydrodynamic Traffic Flow Model with Explicit Drivers’ Physical Delay. Nonlinear Dynamic, 71, 531-537. https://doi.org/10.1007/s11071-012-0679-5
- 17. Tang, T.Q., Huang, H.J., Zhao, S.G. and Xu, G. (2009) An Extended OV Model with Consideration of Driver’s Memory. International Journal of Modern Physics B, 23, 743-752. https://doi.org/10.1142/S0217979209051966
- 18. Hu, Y.M., Ma, T.S., and Chen, J.Z. (2014) An Extended Multi-Anticipative Delay Model of Traffic Flow. Communications in Nonlinear Science and Numerical Simulation, 19, 3128-3135. https://doi.org/10.1016/j.cnsns.2014.02.006
- 19. Li, Z.P., Li, W.Z., Xu, S.Z. and Qian, Y.Q. (2015) Analyses of Vehicle’s Self-Stabilizing Effect in an Extended Optimal Velocity Model by Utilizing Historical Velocity in an Envi-ronment of Intelligent Transportation System. Nonlinear Dynamic, 80, 529-540. https://doi.org/10.1007/s11071-014-1886-z
- 20. 陈春燕, 许志鹏, 邝华. 连续记忆效应的交通流跟驰建模与稳定性分析[J]. 广西师范大学学报, 2017, 35(3): 14-21.
- 21. Wang, J.F., Sun, F.X., Cheng, R.J. and Ge, H.X. (2018) An Extended Car-Following Model Considering the Self-Stabilizing Driving Be-havior of Headway. Physica A, 507, 347-357. https://doi.org/10.1016/j.physa.2018.05.042
- 22. Zhang, G., Sun, D.H., Liu, W.N. and Liu, H. (2015) Traffic Stability of a Car-Following Model Considering Driver’s Desired Velocity. Modern Physics Letters B, 29, Article ID: 1550097. https://doi.org/10.1142/S0217984915500979
- 23. Ge, H.X., Cheng, R.J. and Li, Z.P. (2008) Two Velocity Difference Model for a Car Following Theory. Physica A, 387, 5239-5245. https://doi.org/10.1016/j.physa.2008.02.081