International Journal of Mechanics Research
Vol.
08
No.
04
(
2019
), Article ID:
33316
,
9
pages
10.12677/IJM.2019.84026
Simulation and Correction of Large Equivalent TNT Air Explosion Overpressure
Ya Wang, Hong Zhang, Xiang Chen
School of Science, Chang’an University, Xi’an Shaanxi
Received: Nov. 14th, 2019; accepted: Nov. 28th, 2019; published: Dec. 5th, 2019

ABSTRACT
In order to study the explosive characteristics of large equivalent explosives, the LS-DYNA software was used to establish a model for the explosion of large equivalent TNT explosives in air. The calculation result is lower than the empirical formula value and can be used as the lower limit of anti-explosion design. Through the simulation values of different working conditions, the general overpressure function is obtained by fitting, and the numerical simulation results can be directly calculated. The overpressure function is corrected in the form of exponential function, and the universal modified overpressure function is given, which avoids the calculation deviation caused by different empirical formulas. Through data verification, both functions have universal applicability, which can better guide the structural anti-explosion design of large equivalent explosives and facilitate engineering application.
Keywords:Explosion, Numerical Simulation, Large Equivalent, Overpressure Correction
大当量TNT空中爆炸超压的模拟与修正
王雅,张宏,陈翔
长安大学理学院,陕西 西安
收稿日期:2019年11月14日;录用日期:2019年11月28日;发布日期:2019年12月5日

摘 要
为了研究大当量炸药爆炸特性,运用LS-DYNA软件建立了大当量TNT炸药在空气中爆炸的模型,其计算结果低于经验公式值,可作为抗爆设计下限值。通过不同工况的模拟值,拟合得到通用超压函数,可以直接计算数值模拟结果;以指数函数形式对超压函数进行修正,给出通用修正超压函数,避免了不同经验公式计算引起的偏差。经数据验证,两函数均具有普遍适用性,能更好的指导结构针对大当量炸药的抗爆设计,方便工程应用。
关键词 :爆炸,数值模拟,大当量,超压修正

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,爆炸突发引起的灾害问题时有发生,在建筑结构上尤为常见。为了避免建筑物在突发爆炸事件中遭受重创,在结构设计时应当考虑爆炸冲击荷载,提出有效的抗爆设计方法 [1]。为此,有必要对炸药的爆炸特性进行研究。现阶段,对于爆炸冲击荷载在建筑物上的研究集中于小当量炸药,针对大当量炸药的研究较少。考虑到大当量炸药潜在的破坏威力,很有必要对其进行深入研究。目前对于爆炸冲击荷载的研究主要有实验和数值模拟两种方法。一般来说,TNT当量不小于1吨为大当量 [2]。大当量炸药下进行爆炸实验难度较大,所需设备以及实验条件复杂,实验数据难以获得。LS-DYNA软件可以模拟任何复杂结构计算问题,特别适合模拟碰撞、冲击、爆炸等各种非线性动力问题 [3]。本文利用LS-DYNA软件模拟大当量炸药在空气中自由爆炸现象,将数值模拟结果与多个经验公式进行对比,拟合成通用超压函数表达式,并对其合理修正。
2. 空气冲击波传播规律
炸药爆炸时,冲击波在空气中传播会形成双层球形的两个区域,外层为压缩区,内层为稀疏区 [4],如图1所示。压缩区的空气因受到压缩,压力远远超过正常大气压,也称为超压,超压是判断爆炸效应的重要参数之一。本文主要研究的就是超压峰值的变化。在空气冲击波向外传播的过程中,波阵面的压力迅速下降。原因如下:炸药爆炸过程中,产生的冲击波是球形的,随着传播距离的增大,波阵面的面积也在增加,这样就导致,即使在理想状态下,波阵面上单位面积分布的能量也会减小,再加上受空气环境因素的影响,会有不可逆的能量损失产生 [4],所以在波传播的过程中波阵面压力迅速减小,并且初始阶段衰减快,后期衰减速度变小,实验结果显示,衰减是按照指数规律衰减的,如图2所示。
3. 数值模拟和经验公式的对比
3.1. 建立爆炸模型和材料本构关系
本文采用ANSYS分别建立TNT当量为1,2,3,4,5 t时的空气爆炸模型,所有单元均采用solid164单元,炸药采用球体模型,尺寸如表1所示 [2],空气域采用立方体,尺寸为52 m × 52 m × 52 m,示意图如图3,网格尺寸都为0.4 m,采用kg-m-s单位制,为简化计算,考虑到对称性,可以采用部分建模的方式 [5],以1/8的模型进行计算,如图4,爆点设置在角点,在三个对称面设置对称约束,空气域所有边界面设置为无反射边界 [5]。
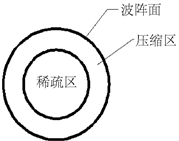
Figure 1. Spherical explosive shock wave propagation diagram
图1. 球形炸药冲击波传播图
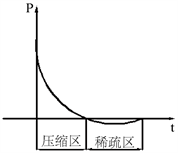
Figure 2. Overpressure decay law
图2. 超压衰减规律
Figure 3. Model plane sketch
图3. 模型平面简图
Figure 4. Entity model diagram
图4. 实体模型图
Table 1. Explosive size
表1. 炸药尺寸
空气采用NULL材料模型以及LINEAR_POLYNOMIAL状态方程 [6] [7],线性多项式状态方程为:
(1)
式中,P为爆轰压力;E为单位体积内能;V为相对体积。参数如表2所示 [2] :
炸药采用HIGH_EXPLOSIVE_BURN模型以及JWL状态方程 [8] [9] :
(2)
式中,P为爆轰压力,V为相对体积,E为单位体积内能,ω、A、B、R1、R2为材料常数。具体参数如表3 [2],其中E0为初始能量,V0为初始相对体积:
Table 2. Air material parameters and equation of state parameters
表2. 空气材料参数和状态方程参数
Table 3. Explosive material parameters and equation of state parameters
表3. 炸药材料参数和状态方程参数
图5为5 t炸药爆炸时,空气冲击波在不同时刻时波阵面的超压云图示例:
 (a) t = 0.005 s (b) t = 0.01 s (c) t = 0.015 s
(a) t = 0.005 s (b) t = 0.01 s (c) t = 0.015 s
Figure 5. Overpressure cloud example
图5. 超压云图示例
3.2. 经验公式
很多学者在理论指导的基础上,结合实验研究,对冲击波超压峰值提出了自己的见解,也总结出以下经验公式(单位:MPa):
1) M.A. Sadovskyi在1952年提出冲击波超压峰值计算公式 [10] :
(3)
2) Henrych公式在1979提出的计算超压峰值的表达式 [10] [11] :
(4)
3) Mills公式在1987年提出的计算TNT爆炸的超压峰值的方法 [11] [12] :
(5)
4) 我国国防工程设计规范(草案)中规定的空爆冲击波超压公式为 [4] :
(6)
5) 王儒策(1993)根据原子爆炸的经验装药提出在无限空气介质中爆炸的超压公式 [13] :
(7)
6) 人民防空地下室设计规范(GB50038-2005) [14] 中提到的公式为:
(8)
其中,Z为比例距离, ,R为测点与爆心的距离(m),W为炸药当量(kg)。
3.3. 结果误差对比
运用LS-DYNA软件计算数值模拟值,采用ALE算法,对经验公式值运用Matlab软件计算。考虑数值模拟的可行性,只针对1~5 t的TNT炸药进行模拟,研究 时各种工况下的超压峰值,结果如图6,图7所示。
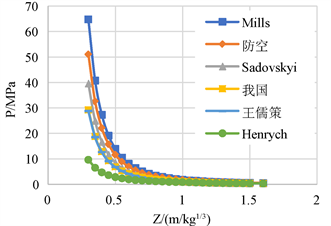
Figure 6. Six formula overpressure peak curve
图6. 六个公式超压峰值变化曲线图
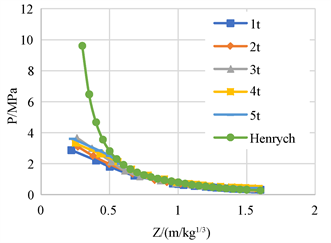
Figure 7. Overpressure peak curve of different equivalent TNT and Henrych formulas
图7. 不同当量TNT和Henrych公式超压峰值变化曲线图
由图6,图7可见:(1) Mills公式算值最大,Henrych公式算值最小,在 时,不同的经验公式之间及其与模拟值均相差较大。(2) 超压峰值随着炸药当量的增加有小幅度增加。(3) 无论是经验公式还是数值模拟结果,超压峰值变化均呈现先迅速下降再缓慢减小趋势,且在 时,他们之间结果基本吻合,说明计算模型和参数选取是合理的。
公式与数值模拟值之间出现差异有两个原因:(1) 经验公式是学者们通过实验研究得出来的,不同学者所处年代,实验设备以及环境条件不同,所得实验结果精确度不同,得出的经验公式有差异,尤其是在 时。(2) 数值模拟是基于理想环境条件建模分析的,而实际爆炸会受到周围环境的影响,比如反射波会对冲击波有加强作用,所以数值模拟值偏小。
3.4. 结果修正
综上可见:如果仅以数值模拟值预测实际爆炸状况,会低估爆炸的威力,存在安全风险。为了准确分析爆炸的威力,本文结合经验公式解,对数值模拟结果进行如下修正。
1) 根据最小二乘法,运用Matlab软件,取5种当量下的超压峰值平均值,拟合得到数值模拟通用超压函数表达式,如式(2.9):
(9)
由图8可得:拟合结果和各当量下的超压曲线吻合程度较大,拟合程度较高。
为了保证抗爆分析的可靠性,在数值模拟值基础上乘以一个修正系数,得到修正后的超压值 ,如式(2.10):
(10)
依据数值模拟解与经验公式值可见,随着比例距离的增大,两者的差距越来越小,且其分布曲线与幂函数和指数函数相似,因此可用二者分别拟合修正系数。取以上六个经验公式的平均值 ,将其作为参考值,使得 接近 ,运用Matlab拟合得到以下两个公式:
幂函数 (11)
指数函数 (12)
对两个函数的拟合结果做误差分析如表4,可得: 的拟合误差控制在6.5%以内,但是 的拟合误差全部控制在2.5%以内,说明两者的拟合程度均较高,但指数函数更为恰当。
其中用到的符号: 为数值模拟解; 为经验公式平均值; 为修正超压值; 为修正系数; 为相对误差的绝对值。
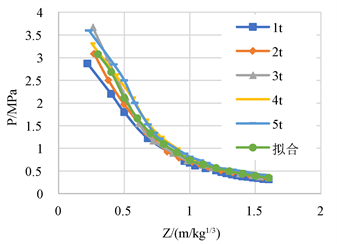
Figure 8. Comparison of simulation results and fitting results
图8. 模拟结果与拟合结果对比曲线
Table 4. Corrected result error
表4. 修正结果误差
2) 为了验证式(2.9)和(2.12)的可靠性,建立6 t的炸药模型,拟合得到图9的对比曲线,结果可见:(a) 公式(2.9)可以很好的反映模拟结果,说明该函数具有普遍适用性;(b) 利用公式(2.12)修正后的结果与经验公式平均值吻合程度较高,说明了该修正系数函数是可靠的。
3) 为了验证式(2.9)和(2.12)的可靠性,建立6 t的炸药模型,拟合得到图9的对比曲线,结果可见:(a) 公式(2.9)可以很好的反映模拟结果,说明该函数具有普遍适用性;(b) 利用公式(2.12)修正后的结果与经验公式平均值吻合程度较高,说明了该修正系数函数是可靠的。
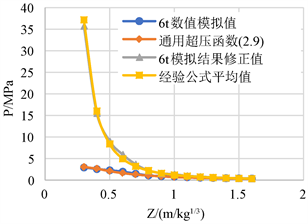
Figure 9. Contrast curve
图9. 对比曲线
4) 综上所述,修正后的冲击波通用超压函数表达式可归纳如式(2.13)。为了在实际中应用方便,直接采用式(2.9)计算数值模拟值,避免繁琐的分析过程及对人员素质要求过高等问题;以式(2.13)计算修正后的超压值,避免采用不同经验公式计算引起的偏差。
(13)
4. 结论
通过上述对大当量TNT爆炸冲击波的超压分析,可得以下结论:
1) 不同的经验公式因为提出的背景、环境有差别,数据之间的差距较大,其中Mills公式值最大,Henrych公式值最小。
2) 运用LS-DYNA软件建立大当量TNT炸药在空气中爆炸的模型,得出数值模拟值比经验公式值小,如果仅以模拟解进行结构抗爆设计,存在低估爆炸威力的风险,但是可作为抗爆设计的下限参考值。
3) 通过不同工况的模拟值,拟合得到通用超压函数表达式(2.9),可以直接计算数值模拟结果,避免工程应用中繁琐的建模分析过程及对人员素质要求过高等问题;通过修正模拟值,归纳出通用修正超压函数表达式(2.13),该公式避免了不同经验公式计算引起的偏差,更好的指导结构针对大当量炸药的抗爆设计。
基金项目
国家自然科学科学基金资助项目(No. 11572235)与(No. 11702034)。
文章引用
王 雅,张 宏,陈 翔. 大当量TNT空中爆炸超压的模拟与修正
Simulation and Correction of Large Equivalent TNT Air Explosion Overpressure[J]. 力学研究, 2019, 08(04): 229-237. https://doi.org/10.12677/IJM.2019.84026
参考文献
- 1. 李忠献, 任其武, 师燕超, 等. 重要建筑结构抗恐怖爆炸设计爆炸荷载取值探讨[J]. 建筑结构学报, 2016, 37(3): 51-58.
- 2. 李宝岩, 戴智涵. 大当量TNT自由空气爆炸数值模拟研究[C]//第26届全国结构工程学术会议论文集(第III册). 北京: 工程力学杂志社, 2017: 96-100.
- 3. 石少卿, 康建功, 汪敏, 等. ANSYS/LS-DYNA在爆炸与冲击领域内的工程应用[M]. 北京: 中国建筑工业出版社, 2011: 18-22.
- 4. 李翼祺, 马素贞. 爆炸力学[M]. 北京: 科学出版社, 1959: 259.
- 5. 李晓勇, 崔村燕, 陈景鹏. LS-DYNA软件开展爆炸冲击波计算时需考虑的问题[J]. 装备学院学报, 2014(4): 79-84.
- 6. (2006) LS-DYNA Keyword User’s Manual. Livermore California: Liver-more Software Technology, Corporation.
- 7. Larcher, M. (2007) Simulation of the Effects of an Air Blast Wave. JRC Technical Note, Institute for the Protection and Security of the Citizen.
- 8. Zhou, T., Yuan, B.-H. and Liang, Z.-F. (2006) Experimental Study of Jet Initiation of Shield PBX. Chinese Journal of Explosives & Propellants, 29, 10-13.
- 9. 吴媛媛, 宋振森. 挡墙后爆炸冲击波绕流现象研究[J]. 河北工程大学学报(自然科学版), 2014, 31(2): 9-14.
- 10. 亨利奇. 爆炸动力学及其应用[M]. 熊建国, 译. 北京: 科学出版社, 1987: 127.
- 11. 杨鑫, 石少鑫, 程鹏飞. 空气中TNT爆炸冲击波超压峰值的预测及其数值模拟[J]. 爆破, 2008, 25(1): 15-19.
- 12. Tolba, A.F.F. (2001) Response of FRP-Retrofitted Reinforced Concrete Panels to Blast Loading. Canada: Carleton University.
- 13. 王儒策, 赵国志. 弹丸终点效应[M]. 北京: 北京理工大学出版社, 1993: 45.
- 14. 中华人民共和国建设部. GB50038-2005. 人民防空地下室设计规范[S]. 北京: 中国计划出版社, 2004.
