ABSTRACT

Median filter technology is a non-linear technology that can preserve image edge while removing noise. It is used widely in many fields, e.g. image enhancing and restoration. In this paper, the principle of median filtering and its characteristic are expatiated. The medium value filter of image was realized with MATLAB software system. The results show that medium value filter is an optimum method in removing image noise.

Keywords:Medium Value Filter, Image Processing, MATLAB

利用中值滤波进行图像处理及其MATLAB实现

黄康强¹，贺宇路²，黄一睿³，黄  琳¹，熊建文^4*

¹中国移动通信集团广东有限公司汕头分公司，汕头

²西安交通大学生物医学信息工程教育部重点实验室，西安

³金山中学，汕头

⁴华南师范大学物理与电信工程学院，广州

Email: xiaoqiang1022@163.com

收稿日期：2014年5月5日；修回日期：2014年5月22日；录用日期：2014年6月4日

摘  要

中值滤波技术是一种在去除噪声的同时能较好保护图像边缘细节的非线性技术，在图像增强和恢复等领域中得到了广泛的应用。文章阐述了中值滤波的原理和特点，并使用软件工具MATLAB实现了图像的中值滤波。结果表明，利用中值滤波法消除图像中的随机噪声是图像噪声处理的最佳方法。

关键词

中值滤波，图像处理，MATLAB

1. 引言

数字图像是建立在人眼的感光特性和大量变换、处理、传输等应用技术基础之上的，在其形成、传输、接收和处理过程中，不可避免地存在着一定程度的噪声干扰，而图像的噪声是影响人眼观察的最直接、最有害和最关键的问题，如何使得图像在终端画面上即保持显示图像的各类要素信息、并得以加强，又适合人眼观察，还能合理地消除大量的噪声是图像处理研究领域进行的主要研究之一[1] [2] 。去噪即滤波，通常可分为线性滤波和非线性滤波两类。对受到噪声污染的退化图像的复原可以采用线性滤波方法来处理，在许多情况下是很有效的，但是多数线性滤波具有低通特性，在去除噪声的同时也使图像的边缘变模糊，不能获得较好的复原效果[3] 。而中值滤波是一种去除噪声的非线性处理方法，在某些条件下既可去除噪声又能保护图像边缘，加之，中值滤波对图像信号的衰减不影响人眼对图像的感觉，因此通过中值滤波能获得较好的图像复原效果。自Turky在1971年提出中值滤波技术以来，该技术就得到了广泛的应用，并被应用到语音处理、图像恢复等领域中[4] -[6] 。近年，江景涛教授课题组[7] 从人眼的结构和视觉特性出发深入研究了图像中噪声产生的机理和消除的方法，提出了利用中值滤波法消除图像噪声的实用方法，通过对影响图像信号的不同噪声采用了不同的滤波方法，并对信号的频谱和滤波的效果进行了研究和分析。

2. 中值滤波技术

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术。这种滤波器的优点是运算简单而且速度快，在滤除叠加白噪声和长尾叠加噪声方面显示了极好的性能。而且中值滤波器在滤除噪声的同时能很好地保护图像边缘，使图像较好地复原。另外，中值滤波器很容易自适应化，从而可以进一步提高其滤波性能。因此，它就非常适应于一些线性滤波器无法胜任的数字图像处理应用场合。

2.1. 中值滤波的基本原理[8] [9]

中值滤波其基本原理是把数字图像或数字序列中一点的值用该点的一个领域中各点值的中值代替。中值的定义如下：一数组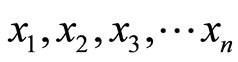，把n个数按值的大小顺序排列于下：，

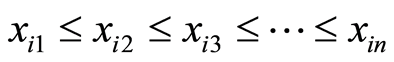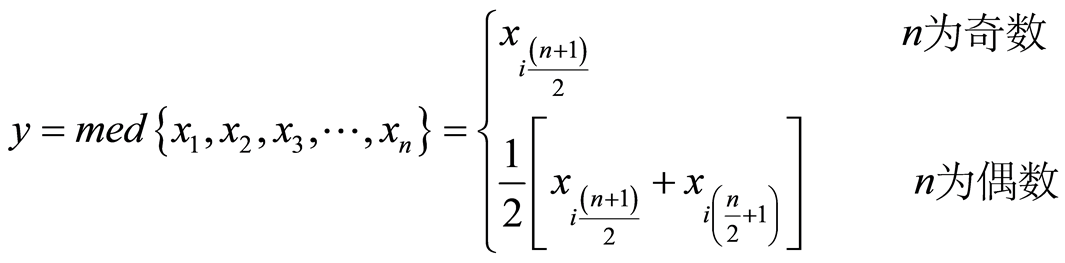
y称为序列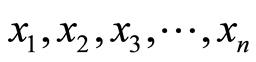的中值。把一个点的特定长度或形状的领域称为窗口。在一维情况下，中值滤波器是一个含有奇数个像素的滑动窗口，窗口正中间那个像素的值用窗口内各像素值的中值代替。

设输入序列为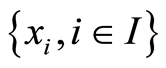，I为自然数集合或子集，窗口长度为n，则滤波器输出为

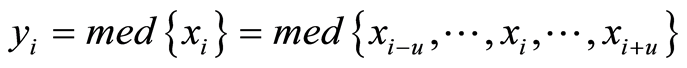
式中，；u = (n − 1)/2。

很容易将中值滤波的概念推广到二维，此时可以利用某种形式的二维窗口。设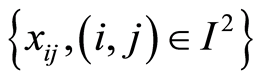表示数字图像各点的灰度值，滤波窗口为A的二维中值滤波可定义为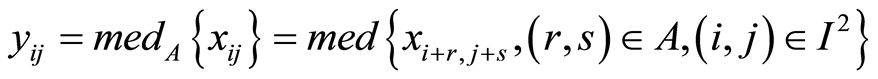二维中值滤波可以取方形，也可以取近似圆形或十字形。

简言之，中值滤波的主要原理是：首先确定一个以某个像素为中心点的领域，一般为方形领域；然后将领域中的各个像素的灰度值进行排序，取其中间值作为中心点像素灰度的新值，这里的领域通常被称为窗口；当窗口在图像中上下左右进行移动后，利用中值滤波算法可以很好地对图像进行平滑处理。具体步骤如下：

(1) 将模板在图像中漫游，并将模板中心与图像中心某个像素的位置重合；

(2) 读取模板下各对应像素的灰度值；

(3) 将这些灰度值从小到大排列成一列；

(4) 找出排在中间的一个值；

(5) 将这个中间值赋给对应模板中心位置的像素。

中值滤波的输出像素是由领域图像的中间值决定的，因而中值滤波对极限像素值(与周围像素灰度值差别较大的像素)远不如平均值那么感，从而可以消除孤立的噪声点，又可以使图像产生较少的模糊。

2.2. 中值滤波的主要特性[10]-[12]

2.2.1. 对某些输入信号中值滤波的不变性

对某些特定的输入信号，如在窗口2n + 1内单调增加或单调减少的序列，中值滤波输出信号仍保持输入信号不变，利用这个特点，可以使中值滤波既能去除图像中的噪声，又能保持图像中一些物体的边缘。

2.2.2. 中值滤波去噪声性能

中值滤波是非线性运算，因此对于随机性质的噪声输入，数学分析是相当复杂的。由大量实验可得，对于零均值正态分布的噪声输入，中值滤波输出与输入噪声的密度分布有关，输出噪声方差与输入噪声密度函数的平方成反比。

对随机噪声的抑制能力，中值滤波性能要比平均值滤波差些。但对于脉冲干扰来讲，特别是脉冲宽度小于m/2，相距较远的窄脉冲，中值滤波是很有效的。

2.2.3. 中值滤波的频谱特性

由于中值滤波是非线性运算，输入和输出之间在频率上不存在一一对应关系。故不能用一般线性滤波器频率特性的研究方法。为了能够直观地定性地看出中值滤波输入和输出频谱变化情况，我们采用总体试验观察方法。设G为输入信号频谱，F为输出信号频谱，定义：H = |G/F|实验表明，H是与G有关的，呈不规则波动不大的曲线。

因此，中值滤波频谱特性H起伏不大，其均值比较平坦，可以认为信号经中值滤波后，频谱基本不变，这点认识对从事设计和使用中植滤波器的工作是很有意义的。

2.3. 视觉与中值滤波的关系[13]

图像最终需要由人来观察、辨别、理解。图像与视角之间有着重要的关系。图像质量的好坏和人眼的感光特性是密切相关的。由于人眼对图像的感觉是以亮度感觉为主的，而亮度感觉主要是由人眼的杆状细胞来完成的，杆状细胞对显示图像的感光是人眼多个细胞的平均光。因此，人眼感受的是若干个杆状细胞，对平均光的刺激，而中值滤波所取的图像信号的中值正好适合于人眼杆状细胞的感光。对图像进行中值滤波后，可以很好地消除分布在图像上的各类随机噪声，且不影响图像给人的感觉。在图像传输过程中，外部干扰和系统内部干扰会给图像带来很多的随机噪声干扰，利用中值滤波就能很好地消除这些干扰，而中值滤波对图像信号的衰减又不影响人眼对图像的感觉。因此，利用中值滤波法来消除图像的随机干扰噪声是图像随机噪声消除的最佳方法。

3. MATLAB软件介绍

MATLAB是Maths Works公司的商业软件，是一种直译式语言，其最重要的功能就是进行矩阵的数值运算，它的数值分析、模拟与运算功能非常强大，而且程序结构完整，具有很强的平行移植性，不仅如此，MATLAB语言编程与C语言十分类似，语法简单、易学易用[14] -[16] 。因此，在图像处理、自动控制、语音处理、信号分析等工业领域，MATLAB是研究、开发和分析首选的计算工具。MATLAB提供了强大的矩阵运算和绘图功能，其中，图像处理工具箱(Image Processing Toolbox)提供了将近200种最基本的图像处理函数，利用这些图像处理工具箱， 结合其强大的数据处理能力，我们可不必关心图像文件的格式、读写、显示等细节，而把精力集中在算法研究上，大大提高了工作效率。同时，在测试这些算法时既可方便地得到统计数据，又可得到直观图示。

利用MATLAB语言及其所提供的函数进行图像处理，编程简单、操作方便、可靠性强，能够达到预期的效果。MATLAB工具箱功能非常强大，简化了繁琐的数学计算工作，有效的促进了数字图像处理相关的研究开发工作。

4. 中值滤波在图像处理中的MATLAB实现

源程序如下：

I=imread('D:\myimages\chost.jpg')；%从D盘名为myimages的文件夹中读取。格式为jpg的图像文件chost J=imnoise(I,'salt & pepper',0.02)；%给图像加入均值为0，方差为0.02的淑盐噪声

subplot(2,4,1);

imshow(I);

title('原始图像');

subplot(2,4,2);

imshow(J);

title('加入椒盐噪声之后的图像');

%h=ones(3,3)/9; %产生3 × 3的全1数组

%B=conv2(J,h); %卷积运算

%采用MATLAB中的函数对噪声干扰的图像进行滤波

Q=wiener2(J,[3 3]); %对加噪图像进行二维自适应维纳滤波

P=filter2(fspecial('average',3),J)/255; %均值滤波模板尺寸为3 K1=medfilt2(J,[3 3]); %进行3 × 3模板的中值滤波

K2= medfilt2(J,[5 5]); %进行5 × 5模板的中值滤波

K3= medfilt2(J,[7 7]); %进行7 × 7模板的中值滤波

K4= medfilt2(J,[9 9]); %进行9 × 9模板的中值滤波

%显示滤波后的图像及标题

subplot(2,4,3);

imshow(Q);

title('3 × 3模板维纳滤波后的图像');

subplot(2,4,4);

imshow(P);

title('3 × 3模板均值滤波后的图像');

subplot(2,4,5);

imshow(K1);

title('3 × 3模板的中值滤波的图像');

subplot(2,4,6);

imshow(K2);

title('5 × 5模板的中值滤波的图像');

subplot(2,4, 7);

imshow(K3);

title('7 × 7模板的中值滤波的图像');

subplot(2,4,8);

imshow(K4);

title('9 × 9模板的中值滤波的图像');

得到图像结果如图1所示。

图1. 滤波效果对比图

5. 结论

(1) 采用不同的滤波方法对图像进行滤波，通过进行比较，可以看到：均值滤波和维纳滤波在衰减噪声的同时也会使图像的边界等细节模糊；而采用中值滤波能较好保护图像边缘细节，消除图像的随机噪声效果很好，同时，滤波后的图像又能符合人眼的视觉感觉。这也是中值滤波器受欢迎的主要原因。

(2) 由上图可见，同一种滤波方法并不是窗口越大滤波效果越好。通过比较，3 × 3模板的中值滤波的效果是最好的，随着所使用的中值滤波器尺寸的增大，消除噪声的效果得到增强；但是，图像的细节锐化程度相应降低，图像变得模糊起来。从而造成图像细节信息的丢失，也破坏了图像的精度。因此选择适当大小的中值滤波窗口可以在最大限度的保持图像精度的基础上去除图像噪声。

综上所述，中值滤波在去除噪声的同时能较好保护图像边缘细节信息，解决了多数线性滤波在去噪的同时模糊图像这一缺点，获得了较好的图像复原效果。因此，利用中值滤波法消除图像中的随机噪声是图像噪声处理的最佳方法。

致  谢

文章得到了国家自然科学基金(61072029)、广东省自然科学基金(10151063101000025)和广州市科技计划项目(2010Y1-C111)的大力支持，在此表示感谢。

参考文献 (References)