Journal of Image and Signal Processing
Vol.
08
No.
04
(
2019
), Article ID:
32651
,
6
pages
10.12677/JISP.2019.84027
Abnormal Image Identification Method Used for Optical Proximity Correction
Shunkui Ke
Shanghai Huali Integrated Circuit Manufacturing Corporation, Shanghai

Received: Oct. 2nd, 2019; accepted: Oct. 17th, 2019; published: Oct. 24th, 2019

ABSTRACT
In order to solve the bad performance for the image in the optical proximity correction, in this paper, a solution can be applied in micro chip manufacturing process which was introduced. It can automatically identify abnormal image and filter bad performance data to save a lot of engineering intervene and prevent the data validation.
Keywords:OPC, Abnormal Image, Data, Chip Manufacturing
一种应用于光学临近修正过程中的异常图像识别方法
柯顺魁
上海华力集成电路制造有限公司,上海

收稿日期:2019年10月2日;录用日期:2019年10月17日;发布日期:2019年10月24日

摘 要
为有效解决光学临近修正中的异常图片处理效率低的问题,本文建立一种可应用于芯片制造光学临近修正过程中的异常图像识别方法,能实现自动化的异常图像识别和异常数据过滤,从而有效减少了工程师人工经验干预,既保障了数据采集的有效性。
关键词 :OPC,异常图像,数据,芯片制造

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 概述
集成电路的发展特征是逻辑尺寸不断减小,光刻机波长是制约核心技术发展的决定因素,由于光学临近效应带来的光罩版图图形畸变也是制约集成电路发展的主要障碍。这种由于光波衍射、干涉而使光刻图形与掩模图形产生偏差的现象称为光学临近效应(OPE: Optical Proximity Effect)。在光刻工艺中,现有方法是采用光学临近修正(OPC: Optical Proximity Correction)方法来尽可能地减小掩模版图形投射到硅片图形的变形与偏差,使得曝光后的图形符合设计要求 [1]。
归纳起来,OPC技术的发展经历了:基于规则的OPC修正方法、基于模型的OPC修正方法、曝光辅助图形的应用、光源优化与掩模板优化、反演光刻技术5个发展过程。基于规则的OPC方法,其实现修正的关键是制定规则库。规则库设计的要求是要能够包含原始版图上所要求的所有图形的修正方案,随着技术节点的进一步缩小,基于规则的OPC方法就显得适用性较差 [2] ;基于模型的光学邻近修正的关键是建立精确的光学模型和光刻胶模型,因为每一层掩模版都有上千万个图形,因此不仅要求模型精度高,而且要求计算速度快 [3] ;因原始版图中包含密集分布图形和稀疏图形,密集分布图形的光刻工艺窗口和稀疏图形的光刻工艺窗口是不一样的,这就会导致共同工艺窗口的变小。适用于密集图形的光照条件并不适合稀疏图形的曝光,因此当技术节点发展到90 nm时引入曝光辅助图形(sub-resolution assistant feature, SRAF)来解决这一难题,在实际光刻中,所加入的曝光辅助图形对光线只起到散射作用,不影响实际的晶圆表面光刻成像,因此,光学邻近修正发展成为SRAF + OPC修正的模式 [4]。光源优化与掩模板优化通过截取原始版图上的关键图形分别进行SMO优化,通过SMO优化的结果进行OPC修正,并用于光刻机的光照条件整理,而后将修正好的掩模版进行制造;反演光刻技术与前面所说的OPC技术的目的一样,但其实现方法完全不同。它主要是以晶圆曝光后得到的图形为目标,反演计算出修正掩模版上所需要的图形 [5]。
OPC一直是芯片制造的核心。制约OPC发展的关键是OPC模型的建立与模型的验证,而数据量测是OPC建模和模型验证的基础。目前普遍存在的问题是:量测机台有时不能准确对准、量测条件容易设置错误,目标量测图形未能准确曝光等,导致量测结果都需要工程师结合人工经验进行检查和校正,这不仅在很大程度上加重了工程师的工作负荷。
为有效解决光学临近修正中的异常数据带来的图片处理效率低的问题,本文建立了一种可应用于芯片制造光学临近修正过程中的异常图像识别方法,通过该方法能实现自动化的异常图像识别,从而有效减少了工程师人工经验干预,保障了数据采集的有效性。
2. 技术方法
OPC数据采集过程中的异常图像处理方法,包括:真彩色图形转换、灰度图生成和灰度图均衡化、图像的灰度直方图获取、相邻图像的图形相关系数计算等步骤 [6] [7] [8],能实现自动化的异常图像识别和异常数据过滤,功能模块图如图1所示。
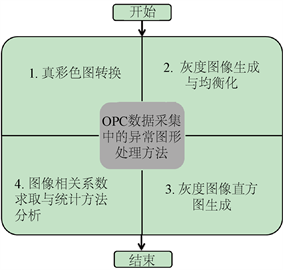
Figure 1. Functional block diagram
图1. 功能模块图
2.1. 真彩色图转换
机台上原始采集的量测图片为红色、绿色、蓝色为基色的真彩色图片,因此在对图片进行预处理转换时,首先要对其进行转换,将其转换级灰度图像,转换公式如下:
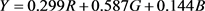 (1)
(1)
公式1中,R、G、B分别为每个像素点对应的RGB颜色分量值,Y为对应该点的灰度值。
2.2. 灰度图生成与均衡化
①、灰度图生成
经过原始图像->灰度图像转换以后,便可得到变化是连续的灰度图 [9]。
②、灰度图均衡化
灰度图均衡化的目的是筛选图片本征,便于计算像素点。通过像素点的灰度计算,便于后续的灰度相关性因素计算。根据之前所生成的灰度图,故可以用下面的公式对其进行均衡:
(2)
公式2中,x为灰度级, 为第i级灰度的像素个数,A0为图像的面积,DMax为最大灰度值。
2.3. 灰度直方图生成
在数字图像处理中,需用灰度直方图带表征灰度图中各灰度级出现的频率。所绘制的灰度直方图如图2,图3所示 [8]。
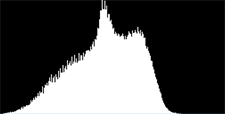
Figure 2. Abnormal image and gray histogram
图2. 异常图像和灰度直方图

Figure 3. Normal image and gray histogram
图3. 正常图像及灰度直方图
2.4. 图像相关系数求取与统计分析
异常图像筛选主要是通过公式(3)分别计算两幅图像的相关程度,来确定图像的相似程度,来达到筛除异常图像的方法。
异常图像的图像相关系数定义为R,用于表征2幅图片中的灰度相关属性,其计算公式如下:
(3)
其中,函数 和 分别是要比较的两幅图像的某种相同属性,R值越大,说明两幅图像的相似程度越高,如图4所示。

Figure 4. Comparison between normal image and abnormal image
图4. 灰度直方图对比
求取的R值结果:0.44,鉴定结果是两幅图片相关度较低。
2.5. 异常图像去除
采用上述方法,对所取得的10张量测图片进行两两比较,根据公式3可得到9个相关性系数R值,如表所示,根据统计学里的四分位数原理,将数列中的小于下四分位数(前三个点对应的图片)删除,即可实现异常图像的过滤,R值计算结果如表1所示,异常图像筛选如图5所示。
Table 1. R value result
表1. R值计算结果
 R = 0.2
R = 0.2
 R = 0.24
R = 0.24
 R = 0.22
R = 0.22
Figure 5. Filtered abnormal image
图5. 被过滤的异常图像
3. 结束语
异常图像处理效率低,且会对OPC相关工作产生重要影响,为有效解决该问题,在图像识别理论的基础上,本文建立一种可应用于芯片制造光学临近修正过程中的异常图像识别方法,该方法通过真彩色图形转换、灰度图生成和灰度图均衡化、图像的灰度直方图获取、相邻图像的图形相关系数计算等步骤,能实现自动化的异常图像识别和异常数据过滤,从而有效减少了工程师人工经验干预,保障了数据采集的有效性。
文章引用
柯顺魁. 一种应用于光学临近修正过程中的异常图像识别方法
Abnormal Image Identification Method Used for Optical Proximity Correction[J]. 图像与信号处理, 2019, 08(04): 215-220. https://doi.org/10.12677/JISP.2019.84027
参考文献
- 1. Shannon, C.E. (1949) Communication in the Presence of Noise. Proc. Institute of Radio Engineers, 37, 10-21.
https://doi.org/10.1109/JRPROC.1949.232969 - 2. Word, J. and Cobb, N.B. (2004) Enhanced Model-Based OPC for 65 nm and below. 24th Annual BACUS Symposium on Photomask Technology, Vol. 5567, 1305-1314.
https://doi.org/10.1117/12.568757 - 3. Cobb, N.B., Zakhor, A. and Miloslavsky, E.A. (1996) Mathematical and CAD Framework for Proximity Correction. SPIE’s 1996 International Symposium on Microlithography, Vol. 2726, 208-222.
https://doi.org/10.1117/12.240907 - 4. Hopkins, H.H. (1951) The Concept of Partial Coherence in Optics. Proceedings of the Royal Society of London, Series A, 208, 263-277.
https://doi.org/10.1098/rspa.1951.0158 - 5. Arthur, G. and Martin, B. (1995) Investigation of Photoresist-Specific Optical Proximity Effect. Micro- and Nano-Engineering ‘95, Aix-en-Provence, France.
- 6. Levenson, M.D., Goodman, D.S., Lindsey, S., Bayer, P.W. and Santini, H.A.E. (1987) The Phase-Shifting Mask II: Imaging Simulations and Submicrometer Resist Exposures. IEEE Transactions on Electron Devices, 31, 753-763.
https://doi.org/10.1109/T-ED.1984.21603 - 7. Nyquist, H. (1928) Certain Topics in Telegraph Transmission Theory. Transactions of the American Institute of Electrical Engineers, 47, 617-644.
https://doi.org/10.1109/T-AIEE.1928.5055024 - 8. Stirniman, J.P. and Cranford, M.D. (2015) Model of Sensitivity of a Simulated Layout to a Change in Original Layout, and Use of Model in Proximity Correction. US 7458059.
- 9. Randall, J., Tritchkov, A.V., Jonckheere, R.M., Jaenen, P. and Ronse, K.G. (1998) Reduction of Mask-Induced CD Errors by Optical Proximity Correction. 23rd Annual International Symposium on Microlithography, SPIE 3334, 124-130.
https://doi.org/10.1117/12.310737
