Software Engineering and Applications
Vol.06 No.05(2017), Article ID:22263,9
pages
10.12677/SEA.2017.65012
The Domination Number of Exchanged Folded Hypercube
Dan Jin, Hongmei Liu, Yanjuan Zhang
College of Science, China Three Gorges University, Yichang Hubei

Received: Sep. 18th, 2017; accepted: Oct. 2nd, 2017; published: Oct. 10th, 2017

ABSTRACT
The exchanged folded hypercube is an attractive variant of the hypercube and obtained by adding some complementary edges from an exchanged hypercube. It not only maintains most of desirable properties of the exchanged hypercube, but also has diameter about half of the exchanged hypercube, and has lower cost factors and constant node degree. In this paper, we will further focus on the properties of exchanged folded hypercube and provide some up bounds for the domination number of exchanged folded hypercube: 1) When , ; 2) When , ; 3) When , , where .
Keywords:Exchanged Hypercube, Exchanged Folded Hypercube, Domination Number, Hamming Code

交换折叠超立方体的控制数
金丹,刘红美,张艳娟
三峡大学理学院,湖北 宜昌

收稿日期:2017年9月18日;录用日期:2017年10月2日;发布日期:2017年10月10日

摘 要
交换折叠超立方体 作为超立方体的变体,是在交换超立方体的基础上增加补边形成的。它不仅保留了交换超立方体结构的大部分拓扑特征,而且直径几乎是交换超立方体的一半,有更低的成本因素和恒定的结点度。本文中,我们将进一步研究交换折叠超立方体的性质,并给出了交换折叠超立方体的控制数的一些上界:1) 当 ,有 ;2) 当 ,有 ;3) ,其中 , , 。
关键词 :交换超立方体,交换折叠超立方体,控制数,Hamming距离

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
超立方体( 维超立方体通常由 表示)是一种具有许多优良的性质的互连网络拓扑结构之一,在工业计算方面和应用开发方面有着广泛的应用,是高性能并行计算机的主要研究课题之一。然而,为了进一步改善超立方体的性能,人们在超立方体的基础上提出了许多变体结构,例如折叠超立方体 ( [1] - [7] )、加强超立方体 ( [8] - [13] )、交叉立方体 ( [14] [15] )、Gaussian cube [16] 、交换超立方体 ( [17] - [22] )等等。
事实上,超立方体有两种类型的变体,第一种是为了提高连通性、缩短传输延迟,可以通过增加一些边来实现,第二种是为了减少成本和复杂度,这种情况可以删除一些边来实现。Ahmed EL-Amawy [7] 提出了 维折叠超立方体 , 是通过在超立方结构中增加边而体形成的,并且被证明 维折叠超立方体的直径大约是 维超立方体的一半,折叠超立方体还具有很多其他优秀的性质。然而,由于折叠超立方体中大量增加的了边的数目,导致硬件成本增加。为了减少边的数量从而减少成本和复杂度,Loh et al. [18] 提出了交换超立方体 ,它是通过从超立方体中删除边形成的,它不仅保持了超立方体网络的许多优良性质,并且有效的将超立方体的边数减少将近一半。虽然 极大程度地减少了互连网络复杂度,但它仍然有一些不足。例如,交换超立方体的直径要远大于折叠超立方体的直径。为了提高交换超立方体和折叠超立方体的性能,一种新的互连拓扑结构交换折叠超立方体 被Heng Qi [23] 提出,是在交换折叠超立方体的基础上通过添加二进制位距离最远的结点组成的,形成的边叫做补边。交换折叠超立方体不仅保留了交换超立方体结构的大部分拓扑特征,同时也结合了折叠超立方体结构的许多优点。交换折叠超立方体的直径几乎是交换超立方体的一半;当网络结构的维度无限大时,交换折叠超立方体 的边数是 维折叠超立方体边数的一半;交换折叠超立方体拥有突出的成本因素,更短的延迟,更少的信息流量密度。关于交换超立方体,已经有了很多非常好的结果。例如 [17] 中对 提出一种时间复杂度为 的最短路由算法;文献 [18] 证明了 能够分解成两个 或者 ,给出了它的直径是 ,指出交换超立方体含有Hamilton圈,可嵌入线性阵列,网格和树等结构;文献 [19] 证明了 和 不是偶泛圈,但是 含有长度从8到 的所有偶圈; [20] 中讨论了交换超立方体的广义容错度量 和 ,证明当 时, ;文献 [22] 提出当 时, 的超连通度和边超连通度为 。然而关于交换折叠超立方体的研究还非常有限,本文中我们主要针对交换折叠超立方体的性质进行探讨。
关于控制数的研究,已经有了很多好的结果。 [24] 给出了一些维度比较小的超立方体的控制数,例如 , , ,并且对于 , ; [25] 中设 是 维Lucas cube,
并证明了 是 的上界,其中 是第 个Lucas数;在文献 [26] 中,令 是 的子图,两个
图的积
是一个图满足下列条件:
,
当且仅当
,或者
。图
的控制数定义为
,文章证明了如果
和 是阶数即顶点个数大于或等于4的任意两个连通图,那么
是他们控制数的一半;在文献 [27] 中证明了如果
是一个控制数为
的
图,则
; [28] 研究了交换超立方体
的控制数,证明了
控制数的上下界,并且证明了对
,
,这里
定义为子图
,
。本文中,我们研究了交换折叠超立方体的控制数,并且给出了交换折叠超立方体的控制数的一些上界:
是阶数即顶点个数大于或等于4的任意两个连通图,那么
是他们控制数的一半;在文献 [27] 中证明了如果
是一个控制数为
的
图,则
; [28] 研究了交换超立方体
的控制数,证明了
控制数的上下界,并且证明了对
,
,这里
定义为子图
,
。本文中,我们研究了交换折叠超立方体的控制数,并且给出了交换折叠超立方体的控制数的一些上界:
1) 当 ,有
2) 当 ,有
3) 当 ,有 ,其中 。
2. 基本概念
在本文中,使图和网络术语我们互换使用,文中所指的图均为简单、有限、无向图。对于文中没有定义的概念与符号请参考文献 [29] 。
设 是一个简单无向图,其中 和 代表点集和边集。集合 ,如果 使得 ,则称集合 为图 的控制集。图 中含顶点数最少的控制集中的元
素个数称为图 的控制数,即可以表示为 。用 来表
示 维超立方体,点集表示为 ,即 中两个每个顶点可以用长为n的二进制位串表示。 中两顶点 和 相邻当且仅当他们只有一位不同。由 表示的 和 之间的Hamming距离是点 和 的对应位串之间的不同位的数量。这里我们用 表示从 中删除两个点 和 后的剩余子图,即 , 和 满足 。
因为交换折叠超立方体 是在交换超立方体 的基础上增加Hamming距离最远两点之间的边的而得到的拓扑结构(这里增加的边定义为补边),因此,我们先介绍 ,再给出 的定义。
交换超立方体 ( , 为整数),其中 :
为了简便,设 ,令 , , 。
边集定义为 :
1)
其中 。
2)
其中 。
3)
其中 。
交换折叠超立方体 是在交换超立方体 的基础上增加补边形成的,补边可以用 来表示,则交换折叠超立方体 定义如下:
为了简便,设 ,令 , , ,即将点 的坐标分成三段 , 和 。
边集 :
1)
其中 。
2)
其中 。
3)
其中 。
4)
由上述定义可知, ,即 是 的生成子图。
通常 中每条边的两个端点互相称为对方的补点,即坐标位表示完全不同的一对点称为补点。比如,点 称为点 的补点。
3. 主要结论
首先介绍一些相关的引理,这些引理对我们的结论的证明非常有帮助。
引理3.1. [28] 如果 ,则 可以被划分为4对(成对不相交)控制集。
引理3.2. [30] 里面的顶点能够被分成等份的控制集,每个控制集的顶点数为 。
引理3.3. [31] 令 ,如果 ,则
定理3.4. 如果 ,则
证明: 的四种边子集如下:
令 为 的属于 中的边子集导出的诱导子图,即 中所有点坐标的表示中,其最左边的s位是一样的,并且最右边的一位固定为1,并且 包含 个与 同构的不交的子图,计为 ,注意每个 与 同构。在两个同构于 的诱导子图 之间是没有边相连的。
类似的,令 为 的属于在 中的边子集导出的诱导子图,即 中所有点坐标的表示中,其中间一段s个坐标位的是一样的,并且最右边的一位固定为0。事实上, 包含 个同构于 的不交子图,计为 。
首先考虑 中的 ,每个 里面有 个点,根据 的定义, 中的每个点都分别有一个邻点和补点在 中,但是同一个点的邻点和补点分布在不同的 中。每个 里面的 个点有 个邻点,这 个邻点恰好分布在 个不同的 中。同理,每个 中的 个点的补点也分布在 个不同的 中。
接下来讨论 的上界。 里面的点可以表示为 ,其中间的一节 是固定的,每固定一个 就有一个 ,因此 有 个同构于 的子图 。考虑这 个 ,由引理3.1,在每个 中选择一个控制集 使
,且每个 中的点全部由一对对最远的点组成,即里面每对点的Hamming
距离为 (这是因为最远点对的坐标只有 是不同的)。则 个 中,每个 里面的点的中间一节 都是不一样的,在同一个 里面的点, 是一样的,最右一位都为0,但是 是可变
的,即有 个不同的 。我们选取的 个 ,每个 之间的 不一样,但是每个 之间拥有相同的 个 。例如在 中。有 个 , 个 ,则我们选取 个 ,使
。 里面的点为00100000和11010000,11000000和00110000; 里面的点为00100010和11010010,11000010和00110010; 里面的点为00100100和11010100,11000100和00110100; 里面的点为00101000和11011000,11001000和00111000; 里面的点为00101100和1101110,11001100和00111100; 里面的点为00101010和11011010,11001010和00111010; 里面的点为00100110和11010110,11000110和00110110; 里面的点为00101110和11011110,11001110和00111110。
在 里面取一点为 ( 中的 是固定的)。在 中, 有一个邻点 ( 是固定的),在 中 有一个补点 ( 是固定的),显然 不在同一个 中。每一个 中与 的 相同, 不同的点的邻点全部在 ,补点在 中,参考图1。但是,在同一个 中, 有一个最远的点记为 , 的邻点在 中,补点在 中,每一个 中与 的 相同, 不同的点的邻点全部在 ,补点在 中。例如 ,每个 中 的点的邻点都在 的 中,补点在 的 中,因为在 中,每固定一个 就有一个 。每个 中 的点的邻点全部在 的 中,补点在 的 中。即 能控制 个 ,且控制 个 。
对剩下的 个 ,令 为剩下的 个 的最小控制集,则
证毕。
定理3.5. 如果 , ,则
证明:因为 ,由引理3.1可知,存在这样的分划使 ,其中每个 都是 的控制集。我们在 的导出子图 中的 个 中选择4个 , 是这4个
的控制集,并且 里面的点由 对最远的点组成,即一对最远的点的Hamming距离
为t,且 , 里面的点的最左边一节 是固定的,4个 即有4个不同的 ,并且4个 里面的点的中间一节 的交集是空集。 里面一对最远的点能控制 两对Hamming距离为s的最远的点,且这两对最远的点不在同一个 里面。参看图2。因为 ,则4个 能控制 个 里面的 对Hamming距离为s的最远的点,这 对点分别在 个不同的 里。
例如在 中,有 个同构于 (为方便,每个就记为 )和在 个同构于 的子图(为方便,每个就记为 ),在 个 中选取4个 , , , , 里面的点全部由一对最远的点构成,因为
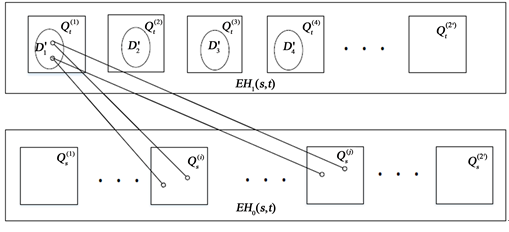
Figure 1. Subgraphs and of
图1. Subgraphs and of

Figure 2. Subgraphs and of
图2. Subgraphs and of
里面的点 是固定的, 是可变的,所以 中一对最远的点可选取为0000001和0001111, 中一对最远的点可选取为0010011和0011101, 中一对最远的点可选取为0110101和0111011, 中一对最远的点可选取为1111001和1110111,显然4个 里的 的交集为空集。 个 的 是固定的,每固定一个 就有一个 ,则令 的 , 的 , 的 , 的 , 的 , 的 , 的 , 的 。 里面的所有点都有一个邻点和补点在 中,例如 里面的点0000001的邻点0000000在 中,补点1111110在 中,0001111的邻点0001110在 中,补点1110000在 中,并且 中的点0000000与点1110000是一对Hamming距离为s的最远的点, 中点1111110和点0001110也是一对Hamming距离为s的最远的点,则 里面一对最远的点可以控制 中两对最远的点,且这两对点不在同一个 中,则 , , , 里面的所有点能控制 个 中8对最远的点,且这8对点分布在不同的 中。
对于 ,令 为 的最小控制集,对 ,令 为 的最小控制集,则
即
定理3.6. 令 ,如果 ,则
证明:由引理3.2可知 里面的顶点能够被分成等份的控制集 。由定理3.4的证明可知 是 的不交并。对 ,令 为 的控制集, 里面的点由 对Hamming距离为t的最远的点组成, ,且 个 里面的点的 交集为空集。证明过
程与定理3.5的证明是类似的,同样, 里面一对最远的点能控制 里面两对Hamming距离为s的最远的点,且这两对点不在同一个 里。因为 ,则 个 能控制 里面的 对Hamming距离为s的最远的点,这 对点分别在 个不同的 里。
对 ,令 为 的最小控制集, 为 的最小控制集。显然 为 的控制集,即
所以 。
4. 总结
网络传输速度,网络可靠性,网络结构复杂度等都是设计网络拓扑结构的关键因素,一个合适的拓扑结构能大大增加网络性能的性价比。交换折叠超立方体 这种互连的拓扑结构不仅保留了交换超立方体结构的大部分拓扑特征,同时也具有折叠超立方体结构的许多优良品质。前人对超立方体,折叠超立方体,加强超立方体,交换超立方体等的研究比较多,但是对交换折叠超立方体的研究不是太多,本文针对交换折叠超立方体进行探讨,主要关注了交换折叠超立方体的控制数问题,并且得到了交换折叠超立方体的控制数的几个上界 , , 。交换折叠超立方体的还有许多其他的性质,我们会进一步研究。
基金项目
本文受国家自然科学基金项目NSFC(11771172)的资助。
文章引用
金 丹,刘红美,张艳娟. 交换折叠超立方体的控制数
The Domination Number of Exchanged Folded Hypercube[J]. 软件工程与应用, 2017, 06(05): 111-119. http://dx.doi.org/10.12677/SEA.2017.65012
参考文献 (References)
- 1. Xu, J.M. and Ma, M.J. (2006) Edge-Fault-Tolerant Properties of Hypercubes and Folded Hypercubes. Australasian Journal of Combinatorics, 35, 7-16.
- 2. Xu, J.M. and Ma, M.J. (2006) Cycle in Folded Hypercubes. Applied Mathematics Letters, 19, 140-145. https://doi.org/10.1016/j.aml.2005.04.002
- 3. Hsieh, S.-Y., Kuo, C.-N. and Huang, H.-L. (2009) 1-Vertex-Fault-Tolerant Cycle Embedding on Folded Hypercubes. Discrete Applied Mathemmatics, 157, 3094-3098. https://doi.org/10.1016/j.dam.2009.06.012
- 4. Yuan, D., Liu, H.M. and Tang, M.Z. (2015) The Connectivity of Faulty Folded Hypercube Networks. 2015 International Conference on Power Electronics and Energy Engineering, 261-265.
- 5. Liu, H.M., Tang, M.Z. and Yuan, D. (2016) Some New Results on Fault-Tolerant Cycles Embedding in Folded Hypercubes. Journal of Combinatorial Mathematics and Combinatorial Computing, 97, 23-36.
- 6. Yuan, D., Liu, H.M. and Tang, M.Z. (2016) Cycles Embedding in Folded Hypercubes with Faulty Nodes. Annals of Applied Mathematics, 32, 69-78.
- 7. El-Amawy, A. and Latifi, S. (1991) Properties and Performance of Folded Hypercubes. IEEE Transactions on Parallel and Distributed Systems, 2, 31-42. https://doi.org/10.1109/71.80187
- 8. Tzeng NF, Wei S. (1991) Enhanced Hypercubes. IEEE Transactions on Computers, 40, 284-294. https://doi.org/10.1109/12.76405
- 9. Qin, R.L. and Liu, H.M. (2015) Cycles Embedding in Conditional Faulty Enhanced Hypercubes. 2015 International Conference on Artificial Intelligence and Industrial Engineering, 233-236. https://doi.org/10.2991/aiie-15.2015.65
- 10. Zhang, Y.J., Liu, H.M. and Liu, M. (2013) Vertex-Fault-Tolerant Cycles Embedding on Enhanced Hypercube Networks. Acta Mathematicae Applicatae Sinica, 33, 1579-1588. https://doi.org/10.1016/S0252-9602(13)60106-X
- 11. Liu, M. and Liu, H.M. (2012) Cycles in Conditional Faulty Enhanced Hypercube Networks. Journal of Communications and Networks, 14, 213-221. https://doi.org/10.1109/JCN.2012.6253071
- 12. Liu, M. and Liu, H.M. (2013) Paths and Cycles Embedding on Faulty En-hanced Hypercube Networks. Acta Mathematica Scientia, 33B, 227-246. https://doi.org/10.1016/S0252-9602(12)60207-0
- 13. Liu, M. and Liu, H.M. (2016) Vertex-Fault-Tolerant Cycle Embedding on Enhanced Hypercube Networks. Acta Mathematicae Applicatae Sinica, English Series, 32, 187-198. https://doi.org/10.1007/s10255-016-0547-z
- 14. Efe, K. (1992) The Crossed Cube Architecture for Parallel Computing. IEEE Transaction on Parallel and Distributed System, 3, 513-524. https://doi.org/10.1109/71.159036
- 15. Hsu, H.S., Fu, J.S. and Chen, G.H. (2007) Fault-Free Hamiltonian Cycle in Crossed Cubes with Conditional Link Faults. Information Sciences, 177, 5664-5674. https://doi.org/10.1016/j.ins.2007.05.032
- 16. Hsu, W.J., Chung, M.J. and Hu, Z. (1996) Gaussian Network for Scalable Distributed Systems. The Computer Journal, 39, 417-426. https://doi.org/10.1093/comjnl/39.5.417
- 17. Tsai, T.-H., Chen, Y.-C. and Tan, J.J.M. (2013) Optimal Edge Congestion of Exchanged Hypercubes. IEEE Transactions on Parallel and Distributed Systems, 27, 250-262. https://doi.org/10.1109/TPDS.2014.2387284
- 18. Loh, P.K.K., Hsu, W.J. and Pan, Y. (2005) The Exchanged Hypercube. IEEE Transactions on Parallel and Distributed Systems, 16, 866-874. https://doi.org/10.1109/TPDS.2005.113
- 19. Ma, M.J. and Liu, B.D. (2009) Cycles Embedding in Exchanged Hypercube. Information Processing Letters, 110, 71-76. https://doi.org/10.1016/j.ipl.2009.10.009
- 20. Li, X.J. and Xu, J.M. (2013) Generalized Measures of Fault Tolerance in Exchanged Hypercubes. Information Processing Letters, 113, 533-537. https://doi.org/10.1016/j.ipl.2013.04.007
- 21. Tsai, T., Chen, Y.C. and Tan, J.J.M. (2014) Topological Properties on the Wide and Fault Diameters of Exchanged Hypercubes. IEEE Transactions on Parallel and Distributed Systems, 25, 3317-3327. https://doi.org/10.1109/TPDS.2014.2307853
- 22. Ma, M. and Zhu, L. (2011) The Super Connectivity of Exchanged Hypercubes. Information Processing Letters, 111, 360-364. https://doi.org/10.1016/j.ipl.2011.01.006
- 23. Qi, H., Li, Y. and Stojmenovic, M. (2015) An Exchanged Folded Hypercube-Based Topology Structure for Interconnection Network. Concurrency and Computation: Practice and Experience, 27, 4194-4210. https://doi.org/10.1002/cpe.3506
- 24. Arumugam, S. and Kala, R. (1998) Domination Parameter of Hypercubes, Journal of the Indian Mathematical Society (N.S), 65, 31-38.
- 25. Castro, A., Klavzar, S., Mollard, M. and Rho, Y. (2011) On the Domination Number and the 2-Packing Number of Fibonacci Cubes and Lucas Cubes. Computers and Mathematics with Applications, 61, 2655-2660. https://doi.org/10.1002/cpe.3506
- 26. Fink, J.F., Jacobson, M.S., Kinch, L.F. and Roberts, J. (1985) On Graphs Having Domination Number Half Their Order. Periodica Mathematica Hungarica, 16, 287-298. https://doi.org/10.1007/BF01848079
- 27. Vizing, V.G. (1965) Abound on the External Stability Number of a Graph. Doklady A. N, 164, 729-731.
- 28. Klavazr, S. and Ma, M.J. (2014) The Domination Number of Exchanged Hypercube. Information Processing Letters, 114, 159-162. https://doi.org/10.1016/j.ipl.2013.12.005
- 29. Xu, J.M. (2001) Topological Structure and Analysis of Interconnection Network. Kluwer Academic Publishers, Dordrecht/Boston/London.
- 30. Jha, P.K. and Slutzki, G. (1995) A Scheme to Construct Distance-Three Codes Using Latin Squares, with Application to the N-Cube. Information Processing Letters, 55, 123-127. https://doi.org/10.1016/0020-0190(95)00066-L
- 31. Jha, P.K. (2015) A Comment on “The Domination Number of Exchanged Hypercubes”. Information Processing Letters, 115, 343-344. https://doi.org/10.1016/j.ipl.2014.09.016