Dynamical Systems and Control
Vol.05 No.04(2016), Article ID:18848,8
pages
10.12677/DSC.2016.54016
Dynamic Properties of Bistable System and Its Application in Forestry Engineering
Xiao Lin, Chunrui Zhang*
Department of Mathematics, Northeast Forestry University, Harbin Heilongjiang

Received: Sep. 30th, 2016; accepted: Oct. 28th, 2016; published: Oct. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The unstable point in the bistable system plays a decisive role and acts as a threshold in image enhancement. Under certain conditions, let the unstable point (that is, the threshold) tend to a stable point in order to achieve the image enhancement. In this paper, a class of bistable systems is studied and the linear stability of the system is analyzed. By using this property, the image histogram equalization is realized by traversing each pixel value at the special time point. Better results.
Keywords:Image Enhancement, Bistable System, Pixel Value, Histogram Equalization

一类双稳系统的动力学性质及其在林业工程上的应用
林啸,张春蕊*
东北林业大学理学院,黑龙江 哈尔滨

收稿日期:2016年9月30日;录用日期:2016年10月28日;发布日期:2016年10月31日

摘 要
双稳系统中的不稳定点对图像增强起到了决定性的作用,使其充当了一个阈值的角色,在一定条件下,使得不稳定的点(也就是阈值)趋于稳定的点,以实现图像增强。本文研究了一类双稳系统,分析了该系统的线性稳定性,利用该性质,在特殊的时间点下,通过初值遍历每一个像素值,实现了图像直方图均衡化,达到了图像增强较好的效果。
关键词 :图像增强,双稳系统,像素值,直方图均衡化

1. 引言
图像增强就是指按照特定的需要去突出一幅图像中的某些信息,同时去除某些不需要信息的处理方法。针对给定图像的应用场合,有目的地强调图像的整体或局部特征,将原来不清晰的图像变得清晰或强调某些感兴趣的特征,扩大图像中不同物体特征之间的差别,使之改善图像质量,丰富信息量,加强图像的识别效果,满足一些较为特殊分析的需要。图像增强有很多种方法,本文介绍基于一类简易双稳系统的图像加强,即将双稳系统看成一个机器,像素值作为输入值,经过机器后,就会有一个输出值,从而达到图像像素值的改变。进一步的说,上述过程只有在系统满足一些特定的条件下才可以实现。
近年来,关于双稳系统的研究有很多,大多是关于随机共振的研究,即在双稳系统与噪声及弱信号的共同作用下达到图像处理的目的。1981年,Benzi提出随机共振的概念时研究了具有双稳态的朗之万(Langevin)方程 [1] 。试想,若只有一个双稳系统图像又是否可以加强呢?在文献 [2] 中,作者提出了一种通过非线性振子实现的图像对比度增强的算法;2008年,Morfu通过雅可比椭圆函数分析了动力系统在不耦合下的解与时间的关系,也强调了阈值的概念,从而实现了图像对比度增强 [3] 。Morfu算法实现的图像处理主要针对低对比度的图片,通过非线性系统作用,可以达到使其对比度增强的目的,而对于像素缺失图片如木材缺陷,该算法是无能为力的。
本文首先引入一个简单的双稳模型,讨论其线性稳定性,得到该系统达到双稳的条件,并利用该系统双稳态下的性质对木材缺陷图片进行纹理增强的处理,使得木材图片纹理更清晰。
2. 双稳系统简介
双稳系统是一种非线性动力学模型,此系统的特点是系统有三个平衡态P,Q和R,其中,P和R是稳定的,而Q态是不稳定的,因此称为双稳系统 [4] 。1981年,Benzi提出随机共振的概念时研究了具有双稳态的朗之万(Langevin)方程,由(1)式描述:
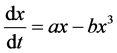 (1)
(1)
其中,系统中的系数a和b为正数,该系统描述了双稳态系统势阱的形状参数。此双稳系统描述了由两个势阱和一个势垒所组成的双稳态系统,系统存在两个对称的势阱,分别对应系统的两个稳定状态 [5] 。图1是非线性系统的分叉图,其稳定性可以用一个小球O在不同形式的势阱中的运动情况来表示,小球O从势垒会朝两个势阱的方向运动,如图2:
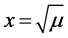

Figure 1. The bifurcation diagram
图1. 分叉图

Figure 2. Bistable potential function
图2. 双稳势函数
如图2,小球在0点易从势垒到两边的势阱。由图1知,系统在 处产生分叉,
处产生分叉,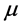 为系统的分叉值。若给定初值
为系统的分叉值。若给定初值 (或
(或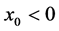 ),系统要趋于稳态解
),系统要趋于稳态解 ,当
,当 时,系统无穷逼近该定态,且再不会离开该定态 [5] 。
时,系统无穷逼近该定态,且再不会离开该定态 [5] 。
3. 一个双稳系统的线性稳定性分析
本文考虑如下双稳系统:
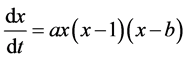 (2)
(2)
其中
求解方程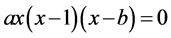 ,显然系统有3个平衡点
,显然系统有3个平衡点 ,
, ,
,
我们分别对系统在个平衡点处的稳定性情况进行讨论:
平衡点为 时,在此平衡点处线性化后得到系统(2)的特征方程为:
时,在此平衡点处线性化后得到系统(2)的特征方程为:


因为特征值小于0,此时系统稳定;
②当平衡点为 时线性化后得到系统(1)的特征方程为:
时线性化后得到系统(1)的特征方程为:

化简得

又 ,
,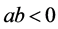 ,
,
特征值大于0,此时系统不稳定;
③当平衡点为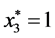 时,在此平衡点处线性化后得到系统(1)的特征方程为:
时,在此平衡点处线性化后得到系统(1)的特征方程为:

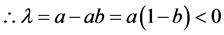
由于特征值小于0,此时系统稳定。
综上,双稳系统(2)在平衡点0与1时为稳定状态;在b时即为不稳定状态。
数值仿真
取系统(2)中的参数, ;在此系数条件下,方程变为
;在此系数条件下,方程变为
 (3)
(3)
分别取系统(3)的初值为:

由上述稳定性分析得知此系统在b = 0.65平衡点处是不稳定的,而在0与1两个平衡点处是稳定的,下面进行数值仿真来分析这四个不同的初值下的解曲线。
取系统(3)的初值分别为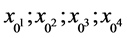 ,仿真的时间区间为[0,20],得到四条解曲线A,B,C,D分别对应四个初值
,仿真的时间区间为[0,20],得到四条解曲线A,B,C,D分别对应四个初值 下的解曲线,图3为仿真结果
下的解曲线,图3为仿真结果
在这四个初值下的解曲线,当初值 时,解曲线收敛到1;当初值
时,解曲线收敛到1;当初值 时,解曲线收敛到0。验证了双稳的定义,三个平衡点中不稳定的点附近的点会朝着两个稳定的点逐渐趋近。在t = 2时,解的变化的范围在[0.2,0.9]之间;在t = 4.5时,解的变化范围在[0,1]之间,且不同的初值下的解之间存在着差值;在t = 8时,解的范围在[0,1]之间,但几乎所有的解都会趋于0附近或者1附近,就会导致在中间值(0,1)的解过少。但当t = 8时也就是大多数灰度级是0或1,中间灰度值为(0,1)的值会偏少,进而不可以实现图像直方图均衡化,从理论上分析在t = 8时图像增强效果不好。
时,解曲线收敛到0。验证了双稳的定义,三个平衡点中不稳定的点附近的点会朝着两个稳定的点逐渐趋近。在t = 2时,解的变化的范围在[0.2,0.9]之间;在t = 4.5时,解的变化范围在[0,1]之间,且不同的初值下的解之间存在着差值;在t = 8时,解的范围在[0,1]之间,但几乎所有的解都会趋于0附近或者1附近,就会导致在中间值(0,1)的解过少。但当t = 8时也就是大多数灰度级是0或1,中间灰度值为(0,1)的值会偏少,进而不可以实现图像直方图均衡化,从理论上分析在t = 8时图像增强效果不好。
由此发现,若给系统一个初值,对应的就会有一个解,且在不同的时间下,解不同。由此可以把双稳系统的性质应用到图像增强上。从图像的灰度上考虑,一幅清晰的图像的灰度变化应是从[0,1]且均匀散开。若把原图像的像素值当做系统的一个初值,经过此双稳系统,在t = 2时灰度级就在[0.2,0.9]间,达不到图像直方图均衡化;当t = 8时也就是大多数灰度级是0或1,中间灰度值为(0,1)的值会偏少,进而不可以实现图像直方图均衡化;但是在t = 4.5时,灰度级为[0,1],且灰度级为均匀散开,可以达到直方图均衡化。若要实现图像增强也就是要把图像对应的直方图均衡化,则系统解的时间就会显得尤为重要,这个问题在下一部分会给出实验结果的分析。
算法具体步骤:
I. 数字图像m ´ n的每一个点(I,j)为一个像素值,把像素值作为初值,也就是输入值,原图像就是输入图像,像素值构成的矩阵为输入矩阵;
II. 通过双稳系统输出方程的解,遍历图像的每一个点,从第一行第一列到第m行第n列,使每一个点都经过双稳系统,每一个点都会有一个输出解,这样就会得到一个与原图像行与列相同的矩阵,作为输出矩阵;
III. 将输出矩阵生成新图像。

Figure 3. Solution curve: Four initial value
图3. 四个初值下的解曲线
4. 木材缺陷图像增强
取一副木材纹理不清图片作为输入图像并利用MATLAB仿真。其中,所选取的图像像素大小为128 ´ 128。
取系统(2)中的参数a = −1,b = 0.65;按照上述算法步骤,图像中的每一个像素值都会经过一次双稳的演化,通过稳定性分析选取tspan = 4.5,实验结果如下图4所示。
图4中的四幅图片从左至右,从上到下依次表示为原木材缺陷图像、经过双稳系统处理后的图像、原木材缺陷图像对应的直方图、经过双稳系统处理后的图像对应的直方图。观察图像,经过双稳系统处理后,原木材缺陷图像中的木结部分被突出出来,其余部分弱化掉,符合图像增强的思想;再观察直方图部分,经过双稳系统处理后,原木材缺陷图像的直方图的灰度级由[0.3,0.8]均衡到[0,1]且灰度级均匀散开。综上,双稳系统可以实现加强,并可以将直方图均衡化。
在上一部分提到的时间t影响图像处理后的效果与质量,下面我们观察在不同的时间t下图像的效果有何变化,从而验证我们的结论。
图5中的四幅图片从左至右、从上至下依次表示为tspan = 2时图像、tspan = 8时的图像、tspan = 2时的图像对应的直方图、tspan = 8时的图像对应的直方图。观察图像,tspan = 2时木结部分开始清晰,但周围的部分还未被弱化掉,从理论的稳定性分析的部分考虑,就是因为在tspan = 2时双稳系统的解还未收敛到1,所以灰度级就只会是[0.2,0.9],此时图像加强处于“未达标”的状态;tspan = 8时,图像部分周围需要被弱化掉的部分已被弱化掉,但是木结部分已经全部变黑,再看它所对应的直方图,灰度级为[0,1],但是在(0,1)上的灰度级过于分散,从稳定性分析的角度来说,就是在这个时间下大多数的解已经收敛到0或1,导致在(0,1)上的解过少,此时可以说图像被“过于”加强了。
从理论上的角度再分析一下“最佳时间”的产生,在第2部分中的稳定性分析中我们选取的最佳时间点的依据是解之间差值的大小,这样才会有图像对比度的产生。我们做第2部分中曲线A与D的差值曲线以及B与C的差值曲线P及Q,见图6,P曲线是初值为0.55以及0.8之间的差值曲线,Q曲线是




Figure 4. Before and after the image progress and its corresponding histogram
图4. 加强前后图像以及与之对应的直方图




Figure 5. tspan =2 and 8 output image and its histogram
图5. tspan = 2和8时的输出图像以及与之对应的直方图

Figure 6. The relationship between the time t and the difference between the solutions under the initial value
图6. 时间t与初值不同下解之间的差的关系
初值为0.6以及0.7之间的差值曲线,若想增强对比度,只需找到解之间相差最合适的点,通过前文的分析,P曲线解之间的差距最合适范围应在[0.5,0.6]之间,Q曲线解之间的差距小于0.5即可,所以当t = [4.5,5.5]时,即为图像增强的最佳时间了。所以不在最佳时间就会产生图5的效果。
5. 结论
本文介绍了一种简单的双稳型系统并对其做了稳定性分析。通过观察其解曲线,选取特定的时间点,达到直方图均衡化,从而实现图像增强。主要结论如下:1) 双稳系统可以实现图像增强;2) 在不同的时间下,图像增强的效果不同;3) 此种模型较简单且实现速率较快。
基金项目
黑龙江省自然科学基金(序号A2015016)。
文章引用
林 啸,张春蕊. 一类双稳系统的动力学性质及其在林业工程上的应用
Dynamic Properties of Bistable System and Its Application in Forestry Engineering[J]. 动力系统与控制, 2016, 05(04): 143-150. http://dx.doi.org/10.12677/DSC.2016.54016
参考文献 (References)
- 1. Benzi, R., Sutera, A. and Vulpiana, A. (1981) The Mechanism of Stochastic Resonance. Journal of Physics A, 14, L453-L457.
- 2. Morfu, S. and Comte, J.C. (2004) A Nonlinear Oscillators Network Devoted to Image Processing. International Journal of Bifurcation and Chaos, 14, 1385-1394.
- 3. Morfu, S., Marouie, P., Nofiele, B. and Ginhac, D. (2008) Nonlinear Systems for Image Processing. Advances in Imaging and Electron Physics, 152, 13-23.
- 4. 张锁春. 可激励系统分析的数学理论[M]. 北京: 科学出版社, 2010: 5-10.
- 5. 赵尔华. 图像二维随机共振研究[D]: [硕士学位论文]. 天津: 天津大学, 2016: 6-10.