Dynamical Systems and Control
Vol.07 No.01(2018), Article ID:23181,16
pages
10.12677/DSC.2018.71002
State Feedback Fault Diagnosis Technology Based on SVM
Zhiming Fang1, Fuzhong Wang2, Bo Yao1
1College of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning
2Department of Basic Education, Shenyang Institute of Engineering, Shenyang Liaoning

Received: Dec. 2nd, 2017; accepted: Dec. 20th, 2017; published: Dec. 27th, 2017

ABSTRACT
In this paper, SVM is used to classify the poles of the system, and the poles generated by the state feedback system without faults and faults are distinguished. And the grid search method is used to find the optimal parameters, and the pole classification method is modeled. In order to realize the real-time monitoring of system pole change, a new method to estimate the system poles by system status is presented. On the basis of the fault diagnosis model, a reliable controller is designed for the corresponding faults. Finally, an example is given to verify the correctness of the pole estimation method, the accuracy of the fault diagnosis and the effectiveness of the reliable controller.
Keywords:Pole Estimation Method, Pole Classification Model, SVM, Fault Diagnosis, State Feedback
基于SVM的状态反馈故障诊断技术
房志铭1,王福忠2,姚波1
1沈阳师范大学数学与系统科学学院,辽宁 沈阳
2沈阳工程学院基础教学部,辽宁 沈阳
收稿日期:2017年12月2日;录用日期:2017年12月20日;发布日期:2017年12月27日

摘 要
本文利用SVM对系统极点进行分类,区分出状态反馈系统无故障和发生故障时分别产生的极点。并利用网格搜寻法寻找最优参数,对极点分类方法进行建模。为了实现对系统极点变化的实时监测,本文给出了一种通过系统状态估算系统极点的新方法。在给出故障诊断模型的基础上,同时对相应的故障设计可靠控制器。最后通过算例验证极点估算方法的正确性和故障诊断的准确性以及可靠控制器的有效性。
关键词 :模板,极点估算方法,极点分类模型,SVM,故障诊断,状态反馈

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
SVM是近年来兴起的一种基于统计学习理论的机器学习算法,以结构风险最小化为原则来训练和建立模型,其算法本质上是一个凸二次优化问题,能够保证找到的极值解就是全局最优解 [1] [2] 。SVM善于解决小样本、非线性和高维数问题,具有结构简单、泛化能力优秀等特点。有些学者将统计学习理论应用到系统辨识和故障诊断领域 [3] [4] ,其中对于支持向量机应用的研究也有了一定的发展 [5] [6] [7] 。一些学者将支持向量机应用到了故障分类中,文献 [8] 和文献 [9] 分别给出了一种基于最小二乘支持向量机的故障分类方案。文献 [10] 和 [11] 将SVM应用到了模糊控制中,并且文献 [11] 对SVM的算法进行了改进,首次提出用一个新的回归来解决最小二乘支持向量机中的问题,使其学习速度得到了提升。
对于传统的可靠控制问题,国内一些学者已经做得比较完备 [12] [13] 。在本文的故障仿真中可以看到,对应部件不同的通道发生故障时,相应的闭环系统极点的变化区域是不同的。本文在此基础上,提出通过SVM对不同故障的极点进行分类,以实现对闭环系统故障的诊断。单通道故障控制器相对于多通道故障控制以及任意单一通道故障控制有着能耗小,保守性低的优势,在实际生产中应用性更强。本文针对这一情况,设计单一通道的故障控制器,针对不同的单一通道故障切换相应的控制器。而在此之前,首先要解决状态估计的问题,对此国内外学者已经做了大量的研究 [14] [15] [16] [17] 。
本文对于故障诊断和分类给出以下方法。首先给出了极点观测器的设计方法,通过对系统实时监测到的状态,实时估计系统极点的变化趋势。其次,通过系统极点的变化趋势,利用SVM对系统极点进行分类,根据不同通道发生故障,系统极点变化区域不同这一特性,实现对故障的实时诊断。最后,根据故障系统诊断的不同类型的故障,对系统实施相应故障的可靠控制。
2. 基于LIB-SVM的控制系统中极点配置问题的故障诊断方法
基于LIB-SVM的状态反馈系统故障诊断的系统原理示如图1。
通过本文提出的方法,可以很好的判断出系统执行器或者传感器出故障的通道,从而切换相应的单通道控制器,使得系统继续保持稳态,达到可靠控制的目的,有效的降低了传统多通道控制器带来的技术难题,并且有效的降低了控制系统的能耗和保守性。
故障诊断系统部件如图2所示,首先通过状态观测器采集到系统的状态信息,下一步将状态信息传入极点观测器,估算出此时的极点位置。最后再由极点分类器根据极点的位置,判断是否有故障,若极点全部在所要配置的区域内,则暂不对其进行控制;若至少有一个极点跳出所配置的区域,则对其进行故障诊断判断出现故障的通道,之后切换相应的单通道故障控制器,使得系统极点重新配置到所要求区域。
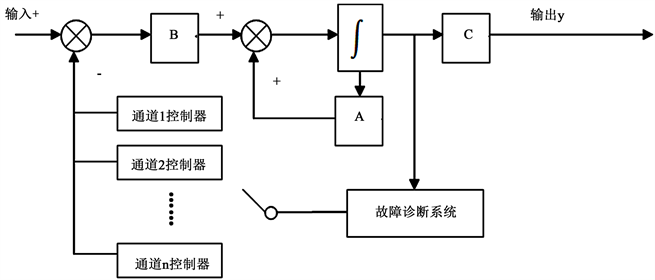
Figure 1. System principle of fault diagnosis for state feedback system based on LIB-SVM
图1. 基于LIB-SVM的状态反馈系统故障诊断的系统原理

Figure 2. Structure of fault diagnosis system
图2. 故障诊断系统结构图
2.1. 状态观测器设计
引理1 [18] :给定n维线性定常系统
(1)
式中,x为n维状态向量,u为p维输入向量,y为q维输出向量,矩阵A,B,C为具有相应维数的实常量矩阵。若此系统是状态完全能观测的,则状态向量 可有输入u和输出y的相应信息构造出来。
状态向量x的重构问题实质上就是根据可直接测量的u和y以及矩阵A,B,C来确定或者产生 的估计值 。将输入 和输出 都利用起来设计状态观测器,如图3。
因为
(2)
所以图3中的状态观测器的动态方程可写成
(3)
由式(3)所表述的动态系统(即状态观测器)所得到的 是与 的维数相同的,故称它为全维观测器。全维观测器是有两个输入 和输出 ,一个输入为状态的估计值 的动态系统。
2.2. 极点观测器设计
2.2.1. 问题描述
设给定自治系统:
(4)
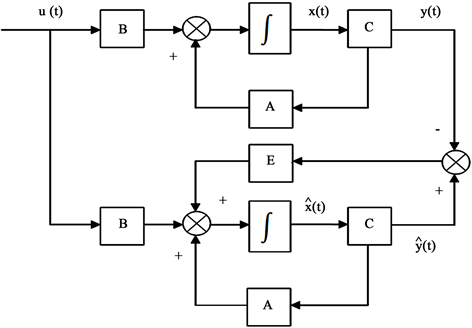
Figure 3. Structure diagram of full dimensional state observer
图3. 全维状态观测器结构图
在已知系统状态可测,通过系统的状态估算系统n阶矩阵A,其中, 为状态, 为采样时间间隔,采样初始时间为 ,采集n + 1个状态值,如下:
2.2.2主要结果
设 ,则 ,可以得到近似计算公式
(5)
其中 越小近似程度越高,通过n + 1个状态值,确定n个状态改变量,设
(6)
也就是,
根据(5)和(6)式,可以得到
根据(6)和上式可得,其中
(7)
以(7)作为矩阵的第 列,可有如下
设n阶矩阵
若 可逆,则得到系统矩阵的估算矩阵 ,
(8)
通过系统仿真发现,t的初值对系统矩阵A无影响, 取值越小,估算出来的A越准确。
2.3. 极点分类器设计
2.3.1. 极点分类器预测模型设计
LIBSVM是中国台湾大学林智仁教授等开发设计的软件对SVM所涉及的参数调节相对比较少,并且提供了很多的默认参数,利用这些默认参数可以解决很多问题。支持向量C-SVC基本原理如下:
给定训练向量集 ,其中 为样本数,将其分成两类 , ,来对下式进行计算:
上述问题的对偶问题是:
其中e为任意向量, ,Q为 的半正定矩阵, , 为核函数。这里的训练集向量 被函数 映射到高维空间中。
其决策函数为:
本文中基于支持向量机方法的极点分类预测仿真实验是利用Libsvm软件包,在matlab中实现的。在进行预测仿真时,首先要采集n个不同通道出现故障时的极点位置数据,把这些数据分成n类。然后对所有数据进行标准化处理,对于每个通道的故障数据,选取其中的一半作为训练集进行建模,另一半数据作为预测的测试集。具体的建模过程如图4所示。
极点数据分类步骤:
1) 收集数据:收集故障部件n条通道分别出现故障时的极点数据,对数据进行标准化处理;
2) 划分训练集与测试集:分别选取n条通道故障时极点数据的一半作为训练集,另一半作为测试集;
3) 将Accuracy作为评价标准,首先建立粗糙预测模型;
4) 参数寻优:采用网格搜寻法,选取最佳的参数c和g,建立模型;
5) 提取模型:提取使Accuracy达到最高的参数c和g,作为预测模型的最终参数建立极点分类模型。
其中参数c表示C-SVC的损失函数,参数g表示核函数中的gamma函数设置(本文中采用的是RBF核函数)。

Figure 4. Modeling process
图4. 建模流程
2.3.2. 极点分类处理
定义1:对复平面中的区域D,如果存在一个对称矩阵 和矩阵 ,使得
则称D是一个线性矩阵不等式区域(简记为LMI区域)。矩阵值函数
称为LMI区域D的特征函数。
定义2:对复平面中给定的LMI区域D和矩阵 ,如果矩阵A的所有特征值都位于区域D中,即 ,则称矩阵A是D-稳定的。
基于以上两个定义,设极点观测器观测到的极点集为 ,若 ,说明所配置的极点跳出了配置区域D,那么我们认为系统出现故障。此时,对观测到的极点进行故障分类,然后切换相应的单通道控制器。若极点仍在所配置区域D内,即使有出现故障的趋势,我们依然认为其稳定,暂不切换控制器,这样使得系统具有一定的鲁棒性。
2.4. 单通道控制器的设计
问题描述
考虑线性定常系统:
(9)
其中, 是状态标量, 是控制变量, 是输出变量,A,B是适维矩阵,C是适维行满秩矩阵。
执行器连续增益故障矩阵模型描述为:
(10)
其中, 为系统的控制输入变量, 为考虑执行器故障系统的输入变量。
引理2:给定的LMI区域 ,则实对称矩阵 是D稳定的充分必要条件是存在一个对称正定实矩阵 使得
其中:
引理3:根据引理1矩阵 的所有特征值均在半径为r,中心在 的圆盘中的充分必要条件是存在对称正定矩阵 ,使得
引理4:在考虑执行器故障时对单故障进行处理(凸组合法),设 ,
设集合
这样由(11)描述的执行器故障矩阵 。存在正整数 ,使得 。显然 是在 和 为顶点构成的凸集合中。因此,总可以找到 满足
使得
3. 主要结果
3.1. 线性系统圆形区域极点配置状态反馈控制器设计
对系统(9)引入状态反馈控制器:
(11)
由此构成闭环系统:
(12)
定理1:对于系统(9),存在状态反馈控制器(11)使得闭环系统(12)的极点配置在半径为r,中心在 的圆盘中的充分必要条件是存在对称正定矩阵X和矩阵Y使得:
存在可行解 和 ,其中 , 为状态反馈增益矩阵。
证明:根据引理1和引理3可知矩阵A的所有特征值均在半径为r,中心在 的圆盘中的充分必要条件是存在对称正定矩阵X,使得
(13)
将(13)中的矩阵 替换成 ,得到
(14)
又由 得到 ,带入(14)有
整理有
定理得证。
3.2. 线性系统执行器故障圆形区域极点配置状态反馈控制器设计
当系统发生执行器故障,由(10)可知系统可以描述为:
对系统(9)引入状态反馈控制器;
由此构成闭环系统:
(15)
定理2:对于系统(15),考虑执行器故障 ,对于系统存在状态反馈可靠控制器的充分必要条件为,对于正定矩阵 和矩阵 ,下列线性矩阵不等式组
存在可行解,若LMIs存在可行解 ,则系统的极点配置到半径为r,中心在 的圆盘区域中,相应的状态反馈可靠控制器增益矩阵为 。
证明:根据引理1和引理3可知矩阵 的所有特征值均在半径为r,中心在 的圆盘中的充分必要条件是存在对称正定矩阵 ,使得
(16)
将(16)中的 替换成 得到
(17)
又由 得到 ,带入(17)有
(18)
又由引理4代入执行器故障得到
定理得证。
4. 系统仿真
考虑如下系统:
希望的闭环系统极点配置在半径为2,中心在 的圆盘区域内
设计状态反馈控制器为
此时闭环系统渐进稳定,极点均配置在所要求的圆盘区域内。
针对此系统收集2条执行器通道分别出现故障时的极点数据,如图5和图6。
建立极点分类器模型的过程中,通过网格搜寻法找到最佳的c和g,建立极点分类模型。寻参如图7和图8。
通过图像可以看出,Accuracy的最佳准平是94.0299%,达到了非常理想的分类水准。
针对2个通道的故障分别切换到相应的单通道控制器,收集极点数据如图9和图10。
下面通过数例验证三个有效性:
第一:极点观测器的有效性。即通过闭环系统状态的信息,估计闭环系统的极点。
第二:极点分类器的有效性。验证极点分类器的分类结果和模拟的故障类型和位置一致。
第三:单通道可靠控制器的有效性。根据故障诊断信息,由相应的可靠控制器构成的闭环系统的极点保持在所配置的区域内。
仿真实验,如下:
第一步:考虑执行器故障 ,其 。此时极点跳出所配置的条形区域,极点位置如图11。
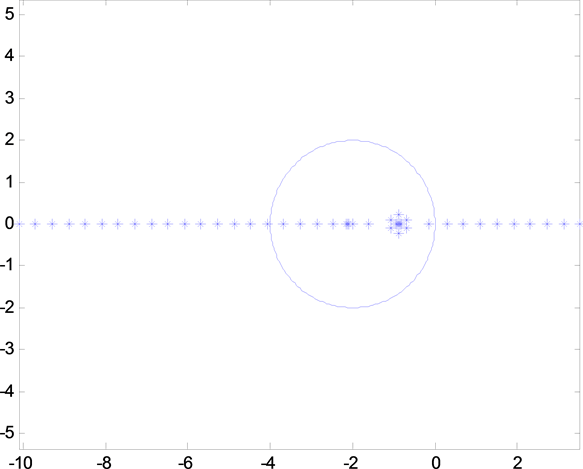
Figure 5. Pole position diagram when channel 1 fails
图5. 通道1出现故障时极点位置图
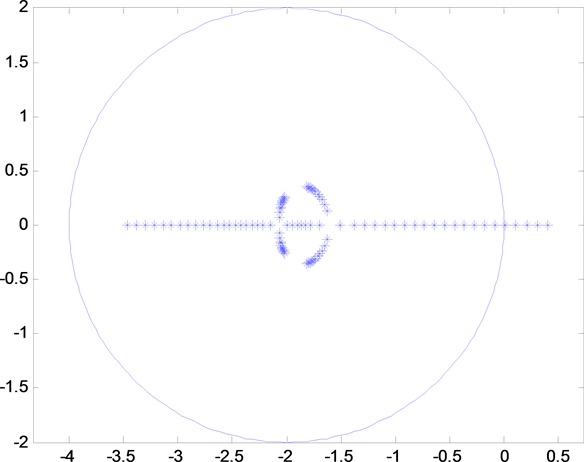
Figure 6. Pole position diagram when channel 2 fails
图6. 通道2出现故障时极点位置图

Figure 7. Parameter selection 3D view
图7. 参数选择3D视图

Figure 8. Parameter selection contour view
图8. 参数选择等高线视图
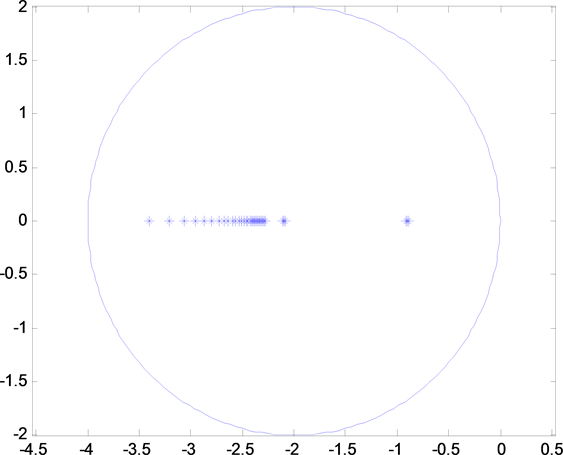
Figure 9. Pole assignment diagram for channel 1 Failure
图9. 针对通道1出现故障的极点配置图

Figure 10. Pole assignment diagram for channel 2 failure
图10. 针对通道2出现故障的极点配置图

Figure 11. Position diagram of fault pole
图11. 故障极点位置图
此时,这三个极点的位置数据为 ,而应用极点观测器的算法采集到的极点数据为 。我们可以看到应用本文中的极点观测器采集到的极点数据与真实数据极为相近。
下面采用本文中极点观测器的设计方法来求观测到的极点集,具体算法如下:
取采样时间为 , , , ;
计算公式为:
此时
根据式子(6)有
可逆,根据式子(8) ,求出:
此时极点集
;
综上,极点观测器的有效性得到了验证。
可以看出极点观测器所观测到的极点非常准确,并且相对误差随着 的缩小而缩小。
第二步:判断 中有一个极点跳出所配置的区域,下面将对极点数据进行分类,然后切换相应的单通道故障控制器。应用本文中的极点分类器建立的极点数据分类模型,模型的参数c = 32,g = 0.5,对这三个极点进行分类,将其预设为第二类故障极点,可以看到预测的故障类型和实际故障类型100%吻合,分类结果如图12。
通过图12,我们可以看到收集到的三个极点,可以准确的分类,此时可以看出发生故障的通道为通道1,与我们所模拟的故障一致,直接验证了极点分类器的有效性。
第三步:对产生故障的极点加上本文所设计的单一通道故障控制器进行极点配置
此时针对通道2的故障,即执行器故障 ,其 ,对其进行极点配置,结果如图13。
通过图13可以看到,极点均配置在了所要求的区域内,验证了单通道可靠控制器的有效性。
5. 结论
综上所述,本文提出的极点观测器,基于LIB-SVM的极点分类器和单通道故障控制器均有效,仿真结果表明,该方法效果良好,能够对系统的极点做出非常准确的观测,分类,以及控制,即极点配置。

Figure 12. Pole classification and prediction
图12. 极点分类与预测情况

Figure 13. Pole assignment diagram
图13. 极点配置图
并且相对于其他方法本文提出的故障诊断及控制方法具有一定的鲁棒性且故障诊断的精度较高,在闭环系统出现故障但不影响系统正常运行,也就是极点位置发生偏移,但均在所配置区域D的情况下,此时可以发出预警,但不切换相应的控制器。只有在极点跳出区域D时,切换相应的控制器。这样可以有效的节约能耗和降低保守性。仿真结果完美地证明了本文结论的有效性。
文章引用
房志铭,王福忠,姚 波. 基于SVM的状态反馈故障诊断技术
State Feedback Fault Diagnosis Technology Based on SVM[J]. 动力系统与控制, 2018, 07(01): 11-26. http://dx.doi.org/10.12677/DSC.2018.71002
参考文献 (References)
- 1. Vapnik, V.N. (1998) Statistical Learning Theory. John Wiley, New York.
- 2. Vapnik, V.N. (1995) The Nature of Statistical Learning Theory. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4757-2440-0 - 3. Yen, C.-W., Young, C.-N. and Nagurka, M.L. (2005) A Training Sample Sequence Planning Method for Pattern Recognition Problems. Automatica, 41, 575-581.
https://doi.org/10.1016/j.automatica.2004.10.012 - 4. 杨娟, 陆阳, 黄镇谨. 基于二进神经网络0/1分布系统可靠性分析[J]. 自动化学报, 2014, 40(7): 1472-1480.
- 5. Ong, C.J., Sui, D. and Gilbert, E.G. (2006) Enlarging the Terminal Region of Nonlinear Model Predictive Control Using the Support Vector Machine Method. Automatica, 42, 1011-1016.
https://doi.org/10.1016/j.automatica.2006.02.023 - 6. Laurain, V., Tóth, R., Piga, D. and Zheng, W.X. (2015) An Instrumental Least Squares Support Vector Machine for Nonlinear System Identification. Automatica, 54, 340-347.
https://doi.org/10.1016/j.automatica.2015.02.017 - 7. Ong, C.J., Keerthi, S.S., Gilbert, E.G. and Zhang, Z.H. (2004) Stability Regions for Constrained Nonlinear Systems and Their Functional Characterization via Support-Vector-Machine Learning. Automatica, 40, 1955-1964.
https://doi.org/10.1016/j.automatica.2004.06.005 - 8. Dubey, H.C., Tiwari, A.K., Nandita and Kishor, N. (2012) A Novel Fault Classification Scheme Based on Least Square SVM. 2012 Students Conference on Engineering and Systems (SCES), IEEE, 1-5.
- 9. Dash, P.K., Samantaray, S.R. and Panda, G. (2007) Fault Classification and Section Identification of an Advanced Series-Compensated Transmission Line Using Support Vector Machine. IEEE Transac-tions on Power Delivery, 22, 67-73.
- 10. Chiang, J.-H. and Hao, P.-Y. (2004) Support Vector Learning Mechanism for Fuzzy Rule-Based Modeling: A New Approach. IEEE Transactions on Fuzzy Systems, 12, 1-12.
https://doi.org/10.1109/TFUZZ.2003.817839 - 11. Zhao, W.Q., Zhang, J.J. and Li, K. (2015) An Efficient LS-SVM-Based Method for Fuzzy System Construction. IEEE Transactions on Fuzzy Systems, 23, 627-643.
https://doi.org/10.1109/TFUZZ.2014.2321594 - 12. 姚波, 王福中. 基于LMI可靠跟踪控制器设计[J]. 自动化学报, 2001(5): 615-619.
- 13. 王福中, 姚波. 基控制于LMI双故障动态输出反馈完整性[J]. 控制理论与应用, 2006(5): 976-980.
- 14. Basher, H.A. (2013) An LMI Approach for Observer Based Model Reference Control. 1-5.
- 15. Juloski, A.L., Heemels, W.P.M.H., Boers, Y., et al. (2003) Two Approaches to State Estimation for a Class of Piecewise Affine Systems. Proceedings of the IEEE Conference on Decision and Control, 1, 143-148.
- 16. 郭胜辉, 朱芳来. 基于区间观测器的执行器故障检测[J]. 控制与决策, 2016, 31(6): 1118-1122.
- 17. 朱芳来, 岑峰, 董学平. 一种基于全维和降维观测器的故障检测和重构方法[J]. 控制与决策, 2011, 26(2): 258-262.
- 18. 张嗣瀛, 高立群. 现代控制理论[M]. 北京: 清华大学出版社, 2006: 219-220.