Dynamical Systems and Control
Vol.
09
No.
01
(
2020
), Article ID:
33435
,
12
pages
10.12677/DSC.2020.91002
The Application of Cybernetics and Dissipative Structure Theory in Ship Maintenance Inventory Management
Guo’an Chen1, Fan Yang2, Qianchao Liang2
1Navy 92730, Sanya Hainan
2College of Power Engineering, Naval University of Engineering, Wuhan Hubei

Received: Nov. 23rd, 2019; accepted: Dec. 6th, 2019; published: Dec. 13th, 2019

ABSTRACT
This paper discusses the application of cybernetics and dissipative structure theory in maintenance management, especially the example of ship maintenance equipment inventory management. For general systems, control theory stresses “regulation” and dissipative structure theory stresses “evolution”, which have different emphases and perfect each other. Dynamic conventional control and dynamic unconventional control can more perfectly and accurately reflect the actual management problems. It is the first time for the analysis method proposed by the author to be applied in the ship maintenance management problem; other topics include discussion of entropy, fluctuations, branching points, and dissipative structures. Finally, a dissipative structure model and application example of inventory system are given.
Keywords:Cybernetics, Dissipative Structure Theory, Maintenance Management, Dynamic Control

控制论与耗散结构论在舰船维修库存管理环节中的应用研究
陈国安1,杨凡2,梁前超2
1海军92730部队,海南 三亚
2海军工程大学,动力工程学院,湖北 武汉

收稿日期:2019年11月23日;录用日期:2019年12月6日;发布日期:2019年12月13日

摘 要
本文探讨了当代科学发展的两个前沿科学控制论和耗散结构论在维修管理问题中的应用,特别例举了舰船维修器材库存管理的例子。对一般系统而言控制理论讲究“调节”、耗散结构理论讲究“演化”,各有不同侧重并相互完善;动态常规控制和动态非常规控制可以更完美更准确地反映实际的管理问题。作者提出的分析方法在船舶维修管理问题中实际应用还是首次,还包括熵、涨落、分支点和耗散结构的讨论,最后给出了一个库存系统的耗散结构模型和应用实例。
关键词 :控制论,耗散结构论,维修管理,动态控制

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现代控制理论和耗散结构理论是当代系统科学发展的前沿,它们展示了动态系统的两类基本调节方式:常规性调节和非常规性调节。在现代维修科学中,应用现代控制论解决管理中的许多问题,在一定条件下已取得了非常满意的效果。然而,在远离平衡条件下,管理问题可能会出现一种不确定状态,有时用控制论来描述这些偶发因素或新结构的产生,也往往会显得力不从心,即使是用随机控制理论也难以解决这种不确定性——不具备统计性质的,完全偶发的因素。对于这类具有真正的不确定性的系统就只能借助于普利高津在研究非平衡态热力学时提出来的耗散结构理论来把握它 [1] [2]。本文试图将这两种理论综合地应用于维修管理,作些有益的探讨,以引起维修界前辈们的兴趣并取得指教。
鉴于控制论 [3] [4] 和耗散结构论的研究范围十分广泛,本文只是以库存管理为例,来探讨这两种理论的应用问题。

Figure 1. Optimal order quantity of the model
图1. 模型最佳定购量
2. 库存问题的提出
库存是现代维修管理的一项重要内容,无论是油库、武器库或机械设备备品库都有一个库存控制问题,既要保证及时满足部队的供给和维修需要,又要注意订购策略,以免占用资金过多或贮备的失效,影响设备的可靠性。因此,存在一个最佳控制和调节问题,因部队一般属于使用部门,故属于“生产–库存”类型,我们称之为“订购–库存”模型。图1所示为这类模型最佳定购量的确定点。
通常“订购–库存”模型有常见的两种类型:
其一,仓库在没有大的战斗损伤或新型舰艇服役时如何根据在役舰艇情况,即机械、油料消耗制定一种策略,既最大限度地满足舰艇需要,又占用资金最少的原则,来订购备件并确定最佳存贮量。
其二,在以上问题的基础上考虑有偶发性海战损坏、风暴损坏和新型舰只加入现役,老设备更换和不断衰亡的情况下,使备件库存和组织结构跟着上其变化。
前者,常用稳态常规动态库存控制,后者则需用非常规动态库存控制。
3. 稳态库存量控制问题
稳态库存控制常用方法有:订购点控制法(定量订购制)和定期库存控制法(定期停购制),而在实施过程中,也可以结合使用ABC库存控制分析法。
一般,无安全库存定量订货存模型见图2所示,对于这种无安全库存模型,通常由费用来确定其数学关系。

Figure 2. Minimum order stock model without safety stock
图2. 无安全库存定最订货存模型
一个周期的总库存费用 = 备件购买费 + 订购费 + 保管费
即:
其中:P-备件单价;S-订购费(单批);D-年需求量;I-贮存保管费;Q-订购量(单批)。
现要求出最佳订购量Q*,使上式总体库存费用C为最小(见图1),可对上式求导得出Q*:
1) 最佳订货量为 (件)
2) 最佳订购次数
由于以上求出的最佳订购量订购次数都是常数,没有考虑到每年中每次订购最的差异,故在实用中有很大局限性,为了求解动态库存管理问题,就得用控制论的方法求解。
4. 动态库存常规控制问题——控制论的应用
现代控制论是从五十年代末、六十年代初发展起来,近来已开始应用于经济系统和管理科学。这是因为它是解决动态管理决策的一个有力工具,例如上述稳态库存问题中,若每次定购量和周期是“动态”的话,用自动控制理论中的动态规划法以及最大值原理都可以得到解决,甚至于70年代末才应用于管理的现代控制论中极点配置,观测器和线性多变量调节器原理也都可以用于解决这类库存控制问题,这里只是简单地介绍一下最大值原理法和动态规划法在库存管理问题中的应用 [5] [6]。
4.1. 动态管理决策过程的数学模型建立
动态管理决策是一个微分方程或差分方程,因应首先搞清楚状态变量,控制变量和外加变量。例如在订购–库存模型中,库存量是状态变量,订货量是决策变量,而需求量则是外部环境对订购库存系统的外加变量。订购量决定着系统状态的变化。之后,可用两种方法来描述系统,一种是黑箱法,其离散时间系统差分方程是:
(1)
另一种是现代控制理论中的状态变量法,即:输入–状态–输出的状态空间表示法,如图3。

Figure 3. Representation of the state space
图3. 状态空间的表示法
离散时间系统的标准式为:
(2)
如果给定向量初值 和输入变量值 ,则由(2)式可以唯一确定状态向量 和输出向量 的值了。例如:
在订购库存模型中,库存量的变化率 等于订购率P(t)减去需求率S(t),即:
(3)
其离散型形式就是差分方程(1)的特例:
(3)1
4.2. 求解订购–库存模型的方法
求解此模型最优控制论有三种方法,即可用动态规则划法,最大值原理变分法及线性多变量调节器来求解。下面介绍变分法和动态规划方法。
订购–库存模型公式:
(4)
决策目标可有两种,所以目标求解也有两种目标函数:
① 订购率P(t),使订购费用C(p,t)和储存费用H(I,t)总和为最小。
即总费用: 最小 (4)1
② 求订购率P(t),使它接近于理想的订购率Pd,即:使库存量I(t)尽量接近理想库存量Id。当系统处于理想稳定状态时,有:
成立
当外界条件变化,平衡将会破坏,则希望通过控制P(t)使系统尽量返回到理想平衡状态。
即:
最小 (5)
式中,h、C常数为加权系统。
从以上模型中可以看出,该管理系统的状态方程(4)是一个线性微分方程,而目标函数(4),或(5)则是一个二次型。所以这是一个线性二次型管理问题的求解,求最优管理决策P(t)使J(p)最小。
解出方程(4)、(5)的解为:
其中: 是方程 的解, (双曲正切函数)
所以最优订购率函数为:
由上式可见,最优订购率P(t)是由理想订购率Pd根据两个因素加以校正的,第一项依赖于原问题中给定的量,第二项依赖于现在的库存量。从直观上我们知道当库存量上升时,订购率下降,即与第二项上升时,第一项下降相一致。
以上求解线性二次型问题,解黎卡提方程较为困难。下面举一个实例,来说明最优控制理论中的动态规划法在解二次型问题较为方便。
例:设某单位每年定购备件A类第K季度为X(K)个,费用为ax2(K)元,某单位仓库每件备品库存费用为b元。设某单位使用计划如表1。
Table 1. Quarterly demand for a unit
表1. 某单位各季度的需求量
又设第K季度初的库存最为Z(k) (状态变量),需求量为S(K),且保证供应,则有状态方程:
要求边界条件
问题是:求解全年订购计划的最优决策X*(t),使之能正好满足要求,又使总费用最小,即目标函数为:
,a,b为加权系数
解:最优控制理论的动态规划原理是一个阶段决策问题。目标函数的最小值为:
(6)
因此,可由后向前推出
第一步,考虑第四季度的控制,令
由方程(6):
又由状态方程:
解出 代入
第二步,考虑3,4两个季度
又由状态方程解出 代入上式

取导数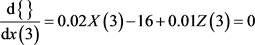

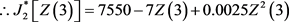
第三步,考虑2,3,4季度
同上,

第四步,考虑全过程



由此解出

结论:最优轨线和最优控制序列如表2。
Table 2. Cost comparison of different ordering methods
表2. 不同订购方式的费用比较
如果各季度按需求订购,则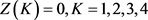 。但总费用为
。但总费用为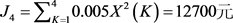 ,比最优决策多用900元。可见最优决策的经济效益是很明显的。
,比最优决策多用900元。可见最优决策的经济效益是很明显的。
关于订购–库存模型的第三种解法:极点配置法和多变量状态观测器设计法是属于现实订购率和理想订购率偏离时,如何调节系统最优化的问题 [7]。
4.3. 订购–库存系统稳定性分析
一个控制系统可分为开环和闭环系统。而实际系统中,为了达到稳定态,往往是通过输出反馈来调节输入大小的闭环系统(见图4),一般对实际库存系统都讨论的是可控、可观测的系统,下面来进行稳定性分析。
李普诺夫对系统的稳定性给出了三种定义:① 稳定;② 渐近稳定;③ 不稳定。
设X为系统平衡态,X0为扰动产生时系统的所处状态。

Figure 4. Closed-loop system with input size adjusted
图4. 调节输入大小的闭环系统
当t > t0时,系统将运动,从X0状态变为X状态有三种趋势,如图6所示。由此定义了系统的三种稳定性,那么,在观测一个系统时,就可以随时间的推移,看到这个系统是停留在所要求的响应附近,还是要发散出去?关于稳定性的判别,所给出的李普诺夫第一、第二法则 [3]。系统的稳定性问题是控制与调节的基本课题,一般情况下,如果该库存系统是不稳定的,那么就要采取反馈调节等外部措施来使系统恢复到稳定状态,因为在控制理论中,不稳定的系统是不可能工作的。对于图5中C的非稳定情况,系统在发散出去以后,会不会达到一个新的稳定组织?在什么条件下,才可能出现这种组织?回答这些问题已超出了现代控制理论的范围,需要引进新的理论和方法,这就是耗散结构理论。

Figure 5. Stability of the system
图5. 系统的稳定性
5. 动态库存非常规控制问题——耗散结构理论及其应用
前面讨论的态库存控制,其核心问题是如何对系统实现最优控制——将系统调节到原稳定状态,都是以下列三条为前提的:
1) 系统处于某种稳定态附近,控制的目的是使系统回到这种稳定态;
2) 对管理系统结构不变,调节之后,也没有出现新的结构,所以系统的数学模型不能改变;
3) 控制和调节的目标已经确定,并在整个过程中保持不变。
然而,实际系统一旦超出这三个方面的限制现代控制理论将无能为力 [8] [9]。库存系统中,新舰艇服役或偶发性海战时,需求将有某种不确定性;再比如老的动力正在被淘汰,与之对应的需求也正在“衰亡”,这些常见的管理问题,控制理论都难以完美解决。因此,我们不得不将系统的这种“演化”,用新的理论–耗散结构来描述。
我们知道,耗散结构理论是研究耗散结构的性质以及它的形成、稳定和演变规律的科学。它有两条可以推广到一般系统。
1) 非平衡是有序之源。
2) 通过涨落达到有序。
要把热力学中耗散结构推广到管理领域,首先要将一些重要的物理概念加以拓展,其中最重要的有“熵”、“涨落”以及“分支点”的确定等等。
5.1. 熵、有序度、涨落和分支点的讨论
热力学第二定律明确提出了孤立系统中的熵增原理或熵产(dis)非负原理。熵在热力学中具有独特的重要地位,且变化和过程的方向密切相关。对不可逆孤立系统的熵总是增加的,代表了系统的“无序度”的增加,或系统由较高的有序度演变为了较低的有序度,而对一个开放系统,总熵总可以表为系统内部的熵产与该系统与外部进行的交换物质和能量所引起的熵产的代数和,即:ds = dis + des (图6)。由上式,系统内部熵产dis ≥ 0,而与外界交换可以使des ≤ 0即有负熵流。这样,就可能使开放系统的总熵ds ≤ 0,这与弧立系统不同。这说明一开放系统在一定条件下,可以使系统的有序度增加。在这种情况下,就可能会出现一种稳定的自组织结构。这与通常我们想象的情形不同,但它揭示了系统宏观的演变规律,在自然界生物进化、相变学及社会、文化中都可以看到这种现象。

Figure 6. Entropy change of non-equilibrium open system
图6. 非平衡开放系统的熵变
从管理学角度来说,一个库存系统是开放的,随着外界环境复杂化,系统会不断地改变着自己的调节、控制方式和管理结构 [10]。这一点已由我军几十年以来后勤物资管理体制的变革所证实。但是,类似这样一种变革或“演化”,是怎么形成的呢?过去都是人为地改变管理形式或者几十年老体系一套不变。缺乏“演化”时机的科学依据,阻碍了我军后勤现代化建设。因此,需要探讨演化需要的条件和实现的机制。
有了熵的定义后,就可以把热力学系统的各种不同的有序状态拿来和管理系统作类比。同时把耗散结构理论的一般方法推广到管理系统中来,从则揭示了管理体系从无序向有序过程的稳定结构形成的机制。
首先,我们可以看到有序可以通过涨落来达到。将管理系统与热力学类比,共有三种不同的稳定方式(见图7)从 到
到 的分支过程。
的分支过程。

Figure 7. Stable way to manage the system
图7. 管理系统的稳定方式
(1)平衡态,系统处于一种稳定状态。对于某一管理系统,输出输入恒定,随时间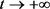 ,系统宏观状态,不发生任何变化
,系统宏观状态,不发生任何变化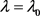 。
。
5.2. 近平衡态分支过程(a)
系统处于“线性非平衡态”,热力学中已证实,这时系统不会出现新的组织结构,对管理系统讲,某单位需求的波动对订购量波动不大,所以库存量波动也不大,即不大的“涨落”,不会引起新的管理结构出现,变革也就不会发生。
5.3. 远离平衡态分支过程(C)
这时由于系统内部强制力迫使系统远离平衡态,系统的新结构和新组织能自发地形成—自组织过程就是耗散结构的形成过程。对管理系统讲,各舰艇各时期需求明显不同,订购率、库存量在时空上分布极不均匀,并带有不好统计概率的某种不确定性。由于远离平衡态,这时系统的微小涨落可能会引起巨涨落,并继续演化而形成一个新的结构——更加有序的自组织结构(如图8),如果我们有目的地去预测这种组织产生的时间和条件,利用其规律性,就可以达到科学、合理地管理之目的。
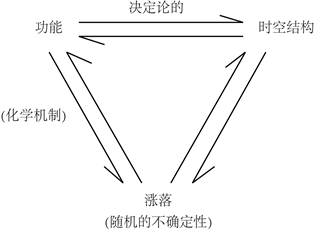
Figure 8. Evolution format of dissipative structure self determined sequence
图8. 耗散结构的演化格式——自决定序列
当离开平衡态 的距离增加时,态的分支过程
的距离增加时,态的分支过程
a)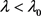 稳定态,近平衡区。
稳定态,近平衡区。
b) 不稳定态。
c)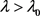 新的稳定态出现。
新的稳定态出现。
对于由涨落而引起的系统结构稳定性问题,我们可以对比图5,在控制理论中曾讨论过的,图5(C)所示的不稳定发散情况,由巨涨落使系统不稳定而发散出去,使得控制失效。那么在一定条件下,使得不稳定结构重新组织成一种新的结构,达到新的稳定态,如图9所示。生物的进化,正是这一过程的不断繁衍,旧组织的破坏和新组织的产生,使生物不断走向有序化,这一点达尔文的生物进化论已证实了,不过前者强调“突变”,而后者则强调“渐近”。管理系统中,管理体制的改革和演变也可以看成前面的类型。
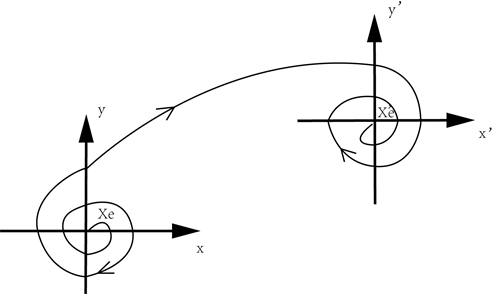
Figure 9. Instability of the original structure and stability of the new structure
图9. 原结构失稳和向新的结构稳定
② 管理系统中,耗散结构模型
我们举一个库存系统中,新的库存系统是如何发生的模型。
在图10所示的三种库存系统中,(5)中分析了它们的比较结果:从I到III的过程是系统负熵不断增加的过程,即向更有序方向进化的过程。那么,在图11中的三分支图中,就是从0 → A → B → C → D的不断进化过程:
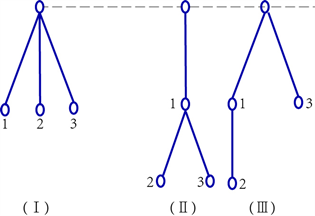
Figure 10. Three inventory systems
图10. 三种库存系统

Figure 11. Branch diagram
图11. 分支图
图11中,从0 → A0时 ,系统I从稳定的平衡态λe由于微涨落而进入到非稳定态,直到临界分支点A,当在点A时,由于我们选择管理策略不同,系统I的状态可能演变为不稳定态,即管理变革失败了。也可能到AF分支的过程或AB分支的过程,这两种稳定态,取决于我们所选择的管理策略,假设我们选择得当的话,系统进入AB分支,就可以到达II的稳定态,即到达B点,在图12中,就可以看到从系统I过渡到II的示意说明。这时结构的有序度提高了,负熵增大了,表示系统结构变革的成功。同理,如果选择得当,系统II会进入BC分支,从而达到又一个新的稳定态,即系统III的产生……库存系统的这种不断演化,就是我们前面所讲到的,一个管理系统中,由于不断地与外界交换信息、物质、能量,在远离平衡条件下,不断地改变着自己的控制方式从而适应了新的环境,新的需求,而达到“进化”之目的 [11]。
,系统I从稳定的平衡态λe由于微涨落而进入到非稳定态,直到临界分支点A,当在点A时,由于我们选择管理策略不同,系统I的状态可能演变为不稳定态,即管理变革失败了。也可能到AF分支的过程或AB分支的过程,这两种稳定态,取决于我们所选择的管理策略,假设我们选择得当的话,系统进入AB分支,就可以到达II的稳定态,即到达B点,在图12中,就可以看到从系统I过渡到II的示意说明。这时结构的有序度提高了,负熵增大了,表示系统结构变革的成功。同理,如果选择得当,系统II会进入BC分支,从而达到又一个新的稳定态,即系统III的产生……库存系统的这种不断演化,就是我们前面所讲到的,一个管理系统中,由于不断地与外界交换信息、物质、能量,在远离平衡条件下,不断地改变着自己的控制方式从而适应了新的环境,新的需求,而达到“进化”之目的 [11]。
图11中的分支点的确定,就是一个很有实用价值的问题,那么对于一个具体的系统来说,可以进一步做的工作就是确定出分支点λC的值,并探讨在何种策略下进入AB分支或AF分支。

Figure 12. Illustrates the evolution from system I to the new system II
图12. 从系统I向新的系统II演化说明
6. 结束语
1) 本文探讨了两种新兴科学——现代控制论和耗散结构理论在管理学中的应用。可以看到,它们相互补充、相互完善。现代控制论的方法是一种常规控制,而耗散结构论的自组织控制是一种非常规控制,对任何一个管理系统的控制,或多或少地同时存在,只是人们没有意识到这一点。例如讨论的仓库管理问题总是存在例行的管理,那么现代控制论正适得其所,大有用武之地。
2) 现代控制理论在管理中的应用比较成熟,因此容易做到常规调节的定量化,而耗散结构理论本身还处在探索之中,定性分析多,而定量工作还有待我们进一步开拓。
3) 现代舰船管理工作要求越来越高,本文提出的分析方法在船舶维修管理问题中实际应用还是首次。其他还包括熵、涨落、分支点和耗散结构的讨论,最后给出了一个库存系统的耗散结构模型和应用实例。对突发库存变化类系统来说,由于总有一些转折关头要用到非例行管理方法,这时系统往往面临一个或几个门坎,而自组织控制正好可以用来预测和制定我们的管理策略。
基金项目
科技创新特区项目(17-163-13-ZT-008-033-01)。
文章引用
陈国安,杨 凡,梁前超. 控制论与耗散结构论在舰船维修库存管理环节中的应用研究
The Application of Cybernetics and Dissipative Structure Theory in Ship Maintenance Inventory Management[J]. 动力系统与控制, 2020, 09(01): 10-21. https://doi.org/10.12677/DSC.2020.91002
参考文献
- 1. 浩峰. 普利高津和耗散结构理论[J]. 自然辩证法通讯, 1982(5): 6.
- 2. 方锦清. 非平衡态研究的最新进展[J]. 自然杂志, 1990(11): 743-751.
- 3. 王照林. 现代控制理论基础[M]. 北京: 国防工业出版社, 2001.
- 4. 孙晓静. 飞轮电池控制策略研究及其应用[D]: [博士学位论文]. 兰州: 兰州理工大学, 2013.
- 5. 付立军, 刘鲁锋, 王刚, 等. 我国舰船中压直流综合电力系统研究进展[J]. 中国舰船研究, 2016, 11(1): 72-79.
- 6. 刘学, 姜新建, 张超平, 等. 大容量飞轮储能系统优化控制策略[J]. 电工技术学报, 2014, 29(3): 75-82.
- 7. 陈泽涛, 金朝永. 线性干扰系统的最优解耦控制[J]. 动力系统与控制, 2019, 8(2): 106-113.
- 8. 贾兴, 孙海义. 复杂网络同步控制方法研究综述[J]. 动力系统与控制, 2018, 7(4): 318-327.
- 9. 张利, 高存臣, 刘云龙. 时滞广义变结构控制研究新进展[J]. 动力系统与控制, 2018, 7(4): 337-347.
- 10. 胡凡. 一部有关管理现代化的教材[J]. 自然辩证法通讯, 1981(6): 78.
- 11. 刘龙英. 动态性经济信息搜集途径刍议[J]. 图书馆论坛, 1999(4): 11-12.
