Open Journal of Transportation Technologies
Vol.06 No.04(2017), Article ID:21222,10
pages
10.12677/OJTT.2017.64017
A Comparative Analysis of Transport Problem with Various Algorithms
Yin Wang1, Jiangping Wang2
1Traffic Portage College, Shanghai Maritime University, Shanghai
2Highway College, Chang’an University, Xi’an Shaanxi

Received: Jun. 14th, 2017; accepted: Jun. 27th, 2017; published: Jun. 30th, 2017

ABSTRACT
As a special kind of linear programming problem, the traditional table on the operation method of the transport problem, its solution process is more complicated. With the development of computer technology, a variety of software plays an important role, such as MATLAB, Lingo and Excel and other software. Based on the Simplex method of linear programming in transportation research, the table operation method of transportation problem and the optimal decision making in decision theory, this paper makes a comparative analysis of several methods to solve the optimal solution of transportation problem.
Keywords:Transportation, MATLAB, Lingo, Excel, The Optimal Solution
多种算法求解运输问题的比较分析
王茵1,王江萍2
1上海海事大学交通运输学院,上海
2长安大学公路学院,陕西 西安
收稿日期:2017年6月14日;录用日期:2017年6月27日;发布日期:2017年6月30日

摘 要
运输问题作为一类特殊的线性规划问题,传统上的表上作业法,求解过程比较繁琐。随着计算机技术的发展,各种软件发挥了重要的作用,例如MATLAB、Lingo以及Excel等软件。本文根据运筹学中线性规划的单纯形法、运输问题的表上作业法,以及决策理论中的优化决策思想,通过实例对几种软件求解运输问题最优解的方法进行了对比分析。
关键词 :交通运输,MATLAB,Lingo,Excel,最优方案

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
货物运输问题一般有多个货源地和对应的多个需求地,如何调配运输线路,使得完成运输任务的同时,运输成本也达到最低,这便是运输寻优问题。
国内学者张晓峰 [1] 研究了用原运输问题的最优解求解新的运输问题;蒋宏锋提出了运输问题的直接算法,根据目标函数的梯度向量在可行域的低维界面上的投影,得出运输问题在可行域上的等值界面,从而直接得出最优解 [2] ;包丽君 [3] 分析了运输问题求解的工作量,利用MATLAB软件辅助,说明了其求解产销平衡的运输问题的主要思想和过程;叶向 [4] 利用电子表格建模,研究了EXCEL在运输问题中的应用;此外还有垂直循环法 [5] 、模糊数学算法 [6] 、遗传算法 [7] 等在运输问题中的应用。
显然,运输寻优问题对节约成本、提高效率、促进运输业发展具有很大的意义。然而传统的寻优方法冗杂、繁琐,因此,积极寻求用计算机技术解决运输寻优问题是一个值得研究的课题。
本文根据一个经典产销平衡运输问题,使用MATLAB、Lingo、Excel、管理运筹学2.0等软件分别求出该问题的最优解,同时对比了各方法实现的精确性和便捷程度。
2. 运输寻优问题的模型建立
在经济建设中,运输问题的最优方案要从各方面综合考虑,使得最终成本达到最小化。
模型的建立流程如图1所示。

Figure 1. Model build flow chart
图1. 模型建立流程图
运筹学 [8] 中关于运输问题数学模型的建立实际上是将系统的复杂问题尽量做到定量化,一般是寻找系统内各特征之间的关系,将其转化为数量指标,根据相应的约束条件确定一个目标函数。
现假设已知产销平衡表和单位运价表,将其综合于同一表内,见表1。
若用xij表示从Ai到Bj的运量,假设前提是产销平衡,要得出总运费最小的运输方案,可建立以下数学模型:
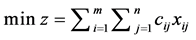
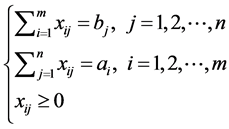
这就是运输问题的数学模型,它包含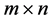 个变量,(
个变量,(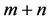 )个约束方程。对产销平衡的运输问题,总有下式存在:
)个约束方程。对产销平衡的运输问题,总有下式存在:
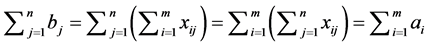
所以模型最多只有 个独立的约束方程,即系数矩阵的秩
个独立的约束方程,即系数矩阵的秩 。
。
3. 运输问题求解方法
3.1. 表上作业法
表上作业法要先得出初始基可行解,也就是初始调运方案,一般采用的是最小元素法,然后应用位势法判断目前的解是否最优,如果不是最优则应用闭回路法进行解的调整,直至最后得到最优方案 [9] 。其求解的流程如下图2所示。
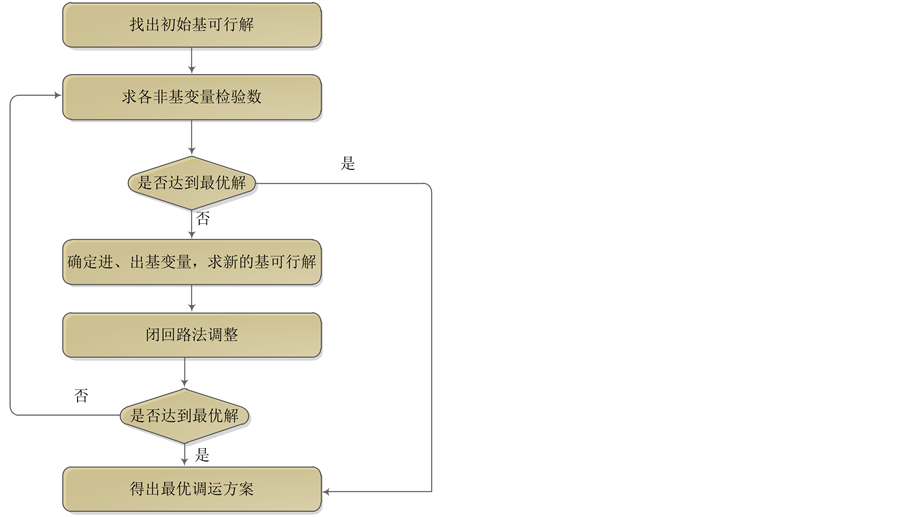
Figure 2. The flow chart of the table-manipulation method
图2. 表上作业法流程图
Table 1. Unit tariff table
表1. 单位运价表
一般而言,用表上作业法求出初始基可行解的方法,包括最小元素法、西北角法、伏格尔法;然后对所求出的解进行最优性检验,检验的方法包括闭回路法、位势法;接下来对得到的解进行改进,改进的方法为闭回路调整法,直到得到该问题的最优解。
3.2. MATLAB中的linprog函数工具箱
MATLAB中解决线性规划的基本函数是linprog函数,其基本调用格式如下:
x=linprog(c,A,b),[x,fval]=linprog(c,A,B,Aeq,Beq,LB,UB,X0,OPTIONS)
其中,x表示规划的解,fval返回目标函数的值,c对应于目标函数的系数,A和B满足Ax ≤ B;Aeq和Beq对应等式约束Aeq∙x=Beq;LB和UB分别是变量x的下界和上界;X0定义了x的初始值,OPTIONS定义了寻优的算法选项。linprog使用的算法一般是linear programming,这是凸优化里最常见的算法之一。
在MATLAB界面建立数学模型,输入格式为矩阵形式,如例子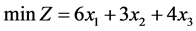 ,然后调用linprog函数,其会根据线性规划的寻优方法自动求解。
,然后调用linprog函数,其会根据线性规划的寻优方法自动求解。
3.3. Excel工具箱规划
在Excel中建立数学模型,如表2和表3,输入已知数据,在规划求解加载项里设置规划求解参数,设定目标单元格和可变单元格,依次添加约束条件,选择求解方法为“单纯线性规划”,并在选项中选择默认的约束精确度和迭代次数,求解后即可快速得到最优运输方案。
3.4. LINGO软件
在lingo中建立数学模型:
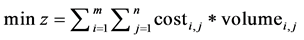 min=@sum(links:cost*volume);
min=@sum(links:cost*volume);
Table 2. Unit tariff table
表2. 单位运价表
Table 3. Shipping volume restrictions
表3. 运量及约束条件
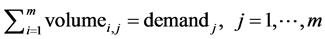 @需求约束;
@需求约束;
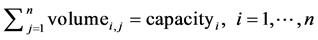 @产量约束;
@产量约束;
首先要定义集,其中,集部分以“sets:”开始,以“endsets”结束,借助于集,能够用一个简明的复合公式表示多个形式相似的约束,从而用较小的篇幅表达出规模较大的模型。
集循环函数@for,@sum,@min定义了目标函数和约束条件,接着根据实例输入已知数据即data部分,运行后可快速得到最优方案和最小运费。
3.5. 管理运筹学软件2.0
管理运筹学软件2.0的数学模型为线性规划下的运输问题,可以自行输入产地个数与销地个数,目标函数也可以根据需要选择最大或最小。
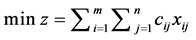
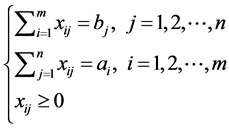
确定产销地数量后,界面会输出一个相应行列的空白表格,根据已知条件,在表格中输入对应产地到对应销地的运费单价,以及产量和销量的约束上限,求解后即可得出最优方案。
4. 实例分析
某百货公司去外地采购A、B、C、D四种规格的服装,数量分别为A-1500套、B-2000套、C-3000套、D-3500套。有三个城市可提供上述规格服装,各城市供应数量分别为:I-2500套,II-2500套,III-5000套 [10] 。
这些城市之间的运输费用不同,详见表4,试确定一个运价最小的采购方案。
4.1. 表上作业法求解
第一步:最小元素法确定初始基可行解;
从最小元素2开始,从Ⅱ城采购B服装2000套,划掉B列,再从余下的运价中找最小元素4,依次用最小元素法找出表中的6、7、8、9,分配给它们相应的采购量,即得到一个初始基可行解。
第二步:位势法判别最优解;
1. 在最小元素法的初始解对应位置填入最小运价,并加入ui列和vj行,令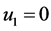 ,根据基变量的检验数等于零,由
,根据基变量的检验数等于零,由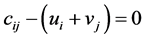 ,依次算出所有ui和vj值。
,依次算出所有ui和vj值。
2. 按 关系,计算所有空格的检验数,如
关系,计算所有空格的检验数,如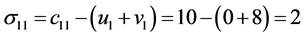 。
。
第三步:闭回路调整法;如果表中空格处的检验数出现了负的,说明未得到最优解,需要用闭回路法来进行改进。
1. 在初始基可行解表上检验数为负数的空格处(3,2)格找出一个闭回路;
2. 利用闭回路调整法进行计算,得到调整方案,见表5。
3. 再用位势法求各空格的检验数。经检验,所有空格处的检验数均非负,则可认为表5的解为最优解,此时得到最小运费为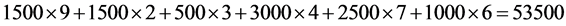 元。
元。
Table 4. Unit tariff table
表4. 单位运价表
Table 5. Optimal transport plan
表5. 最优运输方案
4.2. MATLAB求解
在MATLAB界面对c、a、b分别以矩阵形式赋值,调用linprog函数:
[x,y]=linprog(c,-a,-b,[],[],zeros(4,3))
求得x =1.0e+03 *
[0.0000,0.0000,0.0000,2.5000,0.5980,0.9020, 0.0000,1.0000,0.9020, 1.0980,3.0000, 0.0000]
y = 5.3500e + 04
以上结果显示最终运输方案的费用为53500,但其中的调运数量与表上作业法的解有些出入,我们猜测这是由于MATLAB直接根据代码执行,不能像表上作业法一样进行调整和检验导致。
4.3. Excel求解
在Excel中根据模型输入已知数据,利用规划求解,得出最优方案如图3中黄色区域所示,与表上作业法最小运输费用的结果一致,但运输方案不同。
4.4. Lingo求解
在Lingo中根据模型依次定义集、集循环函数、已知数据,运算后结果如图4所示。
分析图4可以看出,其结果53,500是所求的最低费用,运输方案与表上作业法相同,但与Excel运输方案不同。
4.5. 管理运筹学软件2.0求解
在界面中直接输入算例数据,求得运输问题的最优解,如图5所示。
分析管理运筹学软件输出的结果发现,对于相同的最低费用53500,有两种不同的运输方案,第一种与表上作业法和Lingo相同,第二种与Excel相同。说明“管理运筹学软件2.0”的计算结果优于MATLAB、Excel、lingo和表上作业法。
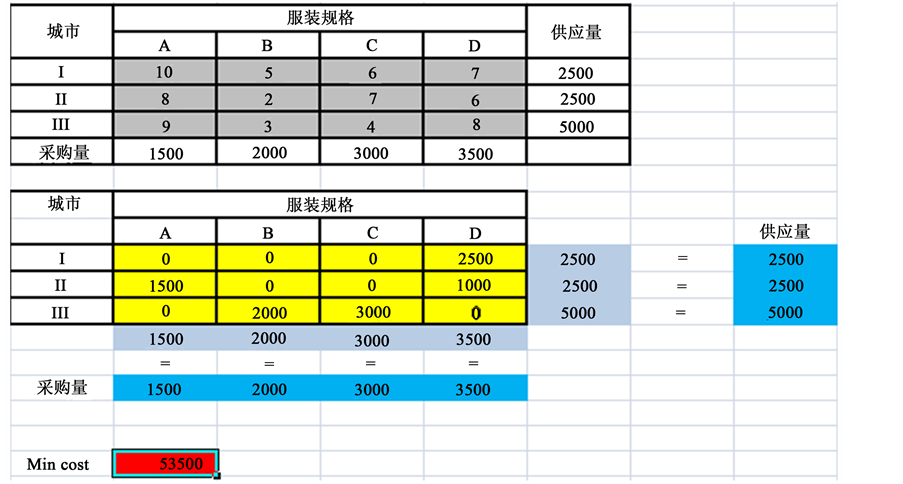
Figure 3. The optimal transport plan from Excel
图3. Excel最优运输方案图

Figure 4. The output graph from Lingo
图4. Lingo输出结果图
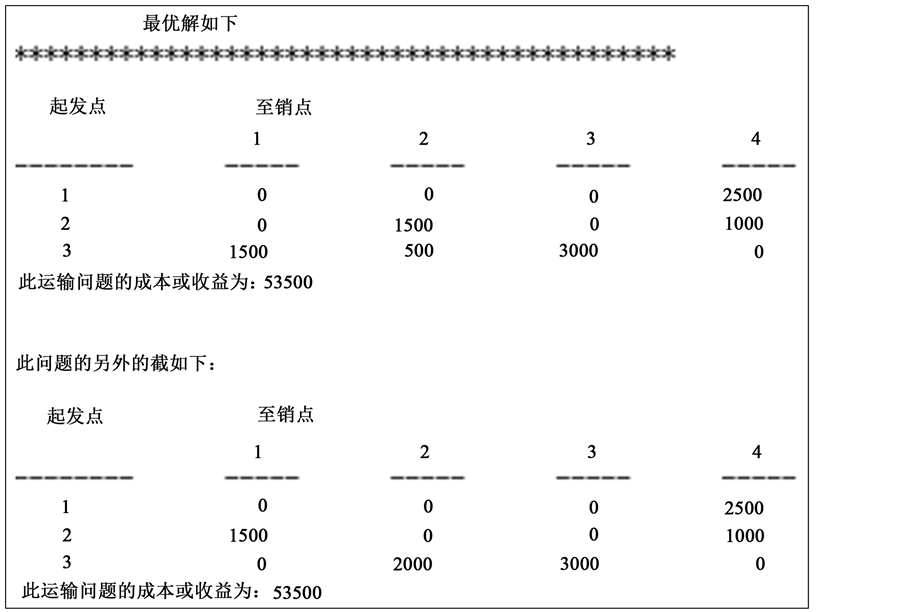
Figure 5. The output chart of manage operations research software 2.0
图5. 管理运筹学软件2.0输出结果图
4.6. 结果对比分析
1) 结果的详细对比分析
表上作业法、MATLAB、Excel、lingo、管理运筹学2.0五种方法的求解结果中最小运费都为53500,但其运输方案有所不同,表上作业法和lingo均求得第一种运输方案{0, 0, 0, 2500, 0, 1500, 0, 1000, 1500, 500, 3000, 0},Excel求得第二种运输方案{0, 0, 0, 2500, 1500, 0, 0, 1000, 0, 2000, 3000, 0},管理运筹学2.0将两种运输方案都得出,MATLAB则求出一种别的方法都未得出的方案{0, 0, 0, 2500, 598, 902, 0, 1000, 902, 1098, 3000, 0}。
2) 计算精度、计算时间的对比分析
虽然表上作业法、lingo均求得第一种运输方案,但表上作业法的的求解精度为1,且往往依赖于人工计算的细心程度,而lingo的输出精度为0.001,远高于表上作业法。MATLAB的默认求解精度为0.0001,且可以根据需要使用vpa函数控制并提高运算精度;Excel的求解精度也可以设置,但大于0.0001时会提示“规划求解找不到有用的解”;管理运筹学软件2.0的求解精度为1。可见MATLAB的精度最高。
另外,若对各方法的求解时间从1~5进行分级,1表示用时最短,5表示用时最长,则表上作业法的求解耗时为5,管理运筹学2.0为1,MATLAB、lingo、Excel的求解时间相当,但由于Excel模型建立迅速,MATLAB、lingo模型建立过程较冗长,所以,Excel用时为3,MATLAB和lingo用时为4。可见,管理运筹学2.0求解最为迅速。
3) 各方法的优劣评价
MATLAB和lingo:用户使用方便,扩充能力强;但编程语句不易快速上手。
Excel:模型易于理解,求解结果清晰直观;但数据量过大时,计算速度会明显下降。
管理运筹学2.0:全图形界面操作,功能强大,易于上手;但结果报表界面不够美观和直观,无法解决一些复杂的交叉综合类问题。
5. 结论与展望
运输问题中一个至关重要的问题便是运输成本的优化,计算最优运输方案,是降低供应链成本、提高效率的重要方法 [11] 。运输问题的算法研究可以使得各种实际中的运输问题得到快速有效的解决,对货物运输乃至物流配送系统的发展都有积极的意义。
本文用五种不同的方法对同一运输问题进行求解,对比分析了各方法的结果,计算精度和计算时间,并评价了各自的优劣,得出以下结论:表上作业法求解最为繁琐;MATLAB求解精度最高;管理运筹学2.0求解速度最快;Lingo求解便捷,但是要准确建立模型,不易快速上手;Excel求解简单明了,但往往会遗漏某些可能的其他最优方案。
当然,此处的结论有限,因为本文仅在这5种方法中做了对比和分析,且案例只涉及产销平衡的运输问题,但总体上求解运输问题的发展趋势还是以开发相应的程序算法为主要方向,这可以极大地简化我们的工作过程、减少工作量,因此,运输寻优问题值得我们更深入的研究,建议可在管理运筹学软件平台上进行开源式的二次开发,则其功能将得到全面提升和完善。
文章引用
王 茵,王江萍. 多种算法求解运输问题的比较分析
A Comparative Analysis of Transport Problem with Various Algorithms[J]. 交通技术, 2017, 06(04): 129-138. http://dx.doi.org/10.12677/OJTT.2017.64017
参考文献 (References)
- 1. 张晓峰. 利用原运输问题的最优解求解新的运输问题[J]. 宁夏大学学报(自然科学版), 1992(3): 41-45.
- 2. 蒋宏锋. 运输问题的直接算法[J]. 科学技术与工程, 2010(17): 4110-4112.
- 3. 包丽君. 基于线性规划法计算运输问题最优解的研究[J]. 宁波广播电视大学学报, 2012(1): 126-128.
- 4. 叶向, 宗骁. Excel在运输问题及其变体中的应用[J]. 中国信息经济学会2006年学术年会, 2006(7): 346-355.
- 5. 吴建平, 吴上民. 垂直循环算法在运输问题中的应用[J]. 吉首大学学报(自然科学版), 2010(4): 31-34.
- 6. 钟波, 张先君, 彭涛. 一类模糊运输问题及其混合智能算法[J]. 重庆大学学报(自然科学版), 2006(7): 95-97.
- 7. 戴庆, 申静波. 基于遗传算法的运输问题最优解研究[J]. 天津理工大学学报, 2008(3): 43-45.
- 8. 冯期. 浅谈运筹学在物流领域中的应用论文[J]. 中国校外教育, 2014(2): 28-29.
- 9. 赵彦艳, 吴桂萍. 运筹学在物流管理中的应用研究[J]. 劳动保障世界, 2013(5): 86-87.
- 10. 张银明. 运筹学的最大元素法及其应用[J]. 华侨大学学报(自然科学版), 2005(2): 55-57.
- 11. 宋玥. 运筹学在企业运输成本优化方面的应用[J]. 经营管理, 2016(10): 3.
