Open Journal of Transportation Technologies
Vol.07 No.03(2018), Article ID:24930,11
pages
10.12677/OJTT.2018.73016
Optimization of Structural Parameters of the Single-Line Tunnel Entrance Hood
Jun Yang, Renxian Li
School of Mechanical Engineering, Southwest Jiaotong University, Chengdu Sichuan

Received: Apr. 26th, 2018; accepted: May 10th, 2018; published: May 17th, 2018

ABSTRACT
The hood, built on high-speed railway tunnel entrance, can reduce pressure pulse effects produced by the train running into tunnels. In order to optimize structural parameters of a single-line tunnel entrance hood, the method of three-dimensional computational fluid dynamics was used to analyze the effects of the length, the sectional area and the opening ratio of an entrance hood on the maximum pressure and the maximum pressure gradient of the initial compression wave in the tunnel. The optimal structural parameters are obtained when the three factors are combined. The results show that the interaction between the length, the sectional area, and the opening area ratio of entrance hood is obvious. The maximum pressure gradient can be reduced effectively when the length is 80 m, the sectional area is 120 m2 and the opening ratio is 40%. Based on this study, the entrance hood with the length of 80 m, the sectional area of 140 m2 and the opening ratio of 20% can effectively reduce the maximum pressure.
Keywords:High-Speed Railway, Entrance Hood of Tunnel, Compression Wave, Numerical Calculation
单线隧道缓冲结构参数的优化
杨军,李人宪
西南交通大学机械工程学院,四川 成都

收稿日期:2018年4月26日;录用日期:2018年5月10日;发布日期:2018年5月17日

摘 要
在隧道入口处修建缓冲结构,可以减缓高速列车进入隧道时产生的入口效应。为了优化单线隧道缓冲结构参数,本文采用计算流体力学三维动态仿真计算的方法,分析了单线隧道缓冲结构的长度、截面积、开孔率对隧道内初始压缩波的最大压力值和最大压力梯度值的影响,得到三个因素综合影响时的最优结构参数。结果表明:缓冲结构的长度、截面积、开孔率对压缩波的交互影响十分明显,且长度为80 m,截面积为120 m2,开孔率为40%时,最大压力梯度值能得到有效降低;在本文研究范围内,缓冲结构长度为80 m,截面积为140 m2,开孔率为20%时,可以有效缓解最大正压值。
关键词 :高速铁路,隧道缓冲结构,压缩波,数值计算

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
高速铁路发展迅速,随着速度不断提高,对隧道空气动力学效应的研究也愈发地重要。高速列车突然进入隧道时,会在隧道入口处产生一个压缩波,压缩波以近似声速的速度沿着隧道方向传播,能量将在隧道出口释放,形成微气压波 [1] 。微气压波是一种脉冲波,会对周围环境产生噪声污染。微气压波与初始压缩波的压力峰值和最大压力梯度值有关,其强度正比于隧道出口处压缩波压力梯度最大值 [2] 。为了减缓列车在隧道内运行时的压力波动和隧道出口的微气压波现象,铁路工程师提出在隧道入口处修建缓冲结构,可以有效地减小初始压缩波的压力峰值和最大压力梯度值。
缓冲结构有多种形式,如直筒形,喇叭形、开孔的和不开孔的缓冲机构,其对隧道初始压缩波的减缓作用也存在较大差别,已有很多文献对上述缓冲结构进行了讨论分析 [3] - [11] 。文献4分析了三种缓冲结构,认为缓冲结构长度越长,截面积越大,则压力梯度值越小,但长度超过隧道等效直径时,影响就会变得很小。文献5分析了喇叭形缓冲结构对隧道内压力变化的影响,认为缓冲结构越长,减压效果越明显,最长达181 m,最优断面扩大率为2~2.5。文献7通过模型实验对缓冲结构进行了分析,认为相对最优的缓冲结构长度在3倍隧道水利直径附近。文献8就350 km/h速度等级的双线隧道分析计算了多种缓冲结构对压缩波的影响,认为长度为20 m、截面面积为150 m2、开2个孔的缓冲结构的减缓效果最佳。
目前各学者对缓冲结构的分析研究结果还没有统一的认识,且大多以双线隧道作为研究对象,研究单线隧道的较少。单线隧道因其较小的截面加上列车的高速运行,其出口处压缩波释放产生的微气压波较之于双线隧道更为明显,适用于双线隧道的缓冲结构不一定能够有效地适用于单线隧道。并且研究方法主要是单因素模型试验法,即只改变一个结构参数,其他参数保持不变。单因素模型试验可以很好地反映单个缓冲结构参数对压缩波的减缓效应。但是,缓冲结构对压缩波的减缓效果是由多个结构参数共同决定的。所以有必要采用多因素交互试验的方法综合分析缓冲结构各个参数对压缩波的影响。本文采用计算流体力学三维动态仿真计算的方法,就300 km/h速度等级单线隧道的缓冲结构进行研究分析,并设计多因素计算方案来研究缓冲结构参数对初始压缩波的影响,进行单线隧道缓冲结构参数的优化。
2. 计算方法与计算模型
高速列车通过隧道时引起的空气流动十分复杂,流动处于紊流状态,采用k-ε方程紊流模型来模拟流场,采用非稳态、黏性、可压缩流的雷诺时均方程来描述列车和隧道的三维流场,方程组的数值求解采用有限体积法 [12] 。
流场计算模型如图1所示,隧道模型为横截面积为我国高速铁路隧道断面形状标准的70 m2的单线隧道,隧道口两边建有长250 m、宽40 m、高20 m的隧道外流场计算区域,在外流场1内隧道入口处设有缓冲结构。缓冲结构为截面积大于隧道截面积的等截面开孔结构,为简化计算模型,在缓冲结构顶部开孔,单个孔洞尺寸为3 m × 2.3 m,通过改变开孔数量可改变开孔率。列车计算模型为CRH3型车,采用三节车编组,头车+中间车+尾车全长75 m。
高速列车通过隧道时,它们之间存在相对运动,为此采用滑移网格技术 [13] 。车体由于其外形复杂,采用四面体网格,如图2所示;隧道和地面采用六面体结构网格。相对运动的不同网格间设置公共滑移界面,从而实现彼此间的数据交换。计算网格经过试算,发现网格数大于300万时计算结果趋于稳定,因此,后续计算各种模型网格数量均控制在300万左右。
为验证计算模型的正确性,将数值分析计算得到的结果与Howe经验公式计算结果进行对比。Howe通过气动声学理论对高速列车进入无缓冲结构隧道时产生的初始压缩波进行了理论推导,适当简化后得到了最大压力值的计算公式 [14] :

式中:ρ为空气密度,v为列车速度,M为马赫数,R为阻塞比。高速列车以300 km/h的速度进入隧道,采用Howe经验公式计算得到的最大压力值为1639 Pa/s,与数值仿真计算结果1602 Pa/s相差2.3%。这表明本文所采用的计算方法与计算模型可以用来分析高速列车通过隧道时所引起的压力变化。
3. 单因素计算结果与分析
根据距隧道入口的距离的不同在无缓冲结构隧道内设多个测点,各个测点压力变化曲线如图3所示,在隧道内100 m~200 m测得的压力变化曲线能够较好地反映压缩波的波形,且峰值稳定。所以本文取隧道内距入口200 m测点处的压力变化情况,分析不同缓冲结构参数对初始压缩波的最大压力值和最大压力梯度值的减缓效果的影响。
带有缓冲结构的隧道内压力和压力梯度值的变化曲线如图4所示,曲线有两个波峰,第一波峰是列车进入缓冲结构入口的过程中由于气体受到压缩所产生的,第二波峰是列车从缓冲结构进入到隧道入口的过程中由于截面发生变化产生的。
为了研究缓冲结构长度对压缩波的最大压力值和最大压力梯度值的影响,分别计算了缓冲结构的长

Figure 1. Computational domain of flow field model
图1. 流场模型计算区域
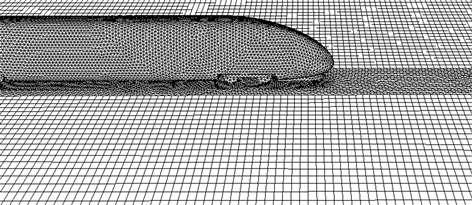
Figure 2. Grid model
图2. 网格模型

Figure 3. Variation of the pressure in the tunnel without hood
图3. 无缓冲结构隧道内压力变化
 (a)
(a)  (b)
(b)
Figure 4. Variation of the pressure and the pressure gradient in the tunnel with hood
图4. 带有缓冲结构时隧道内压力和压力梯度变化。(a) 压力值;(b) 压力梯度值
度分别为0 m(无缓冲结构)、5 m、10 m、20 m、40 m、60 m、80 m、100 m,缓冲结构截面积为100 m2时的模型,计算结果如图5所示。在缓冲结构长度L从0 m增大到10 m的区间内,最大压力梯度值大幅度减小,而最大压力值变化很小;随着L大于10 m之后压力梯度值基本保持在一个稳定的水平,没有明显的变化,但压力值在L从40 m增加到60 m时发生了明显的降低,随后也趋于稳定。
为了研究缓冲结构开孔率对压缩波的最大压力值和最大压力梯度值的影响,计算了缓冲结构长度为60 m,截面积为100 m2,开孔率分别为:0% (无开孔)、20%、30%、40%、60%时的模型,计算结果如图6所示。初始压缩波最大压力值随着开口率增大而不断增大,开口率大于40%后趋于稳定,即缓冲结构
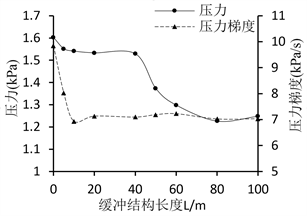
Figure 5. Effect of the length of entrance hood
图5. 缓冲结构长度的影响
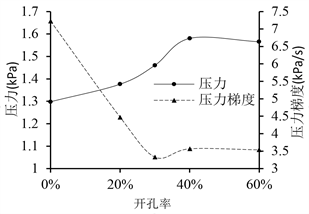
Figure 6. Effect of the opening ratio of entrance hood
图6. 缓冲结构开孔率的影响
开口对降低初始压缩波幅值没有效果,反而导致初始压缩波幅值增大;但最大压力梯度值随开口率的增大而不断减小,当开口率大于30%时,变化不显著。
为了研究缓冲结构截面积对压缩波的最大压力值和最大压力梯度值的影响,计算了缓冲结构长度为60 m,截面积分别为70 m2、100 m2、120 m2、150 m2时的模型,计算结果如图7所示。随着缓冲结构的截面积不断增大,最大压力值不断减小,由于隧道截面积大小(70 m2)的限制,随着S 继续增大,压力值会逐渐趋于稳定;截面积变化对压力梯度的两个峰值的影响十分显著,随着截面积不断增大,压力梯度第一峰值不断减小,第二峰值不断增大,当S = 140 m2时,两峰值相等,即当截面积S = 140 m2时,最大压力梯度值最小,缓冲结构对初始压缩波压力梯度值的减缓效果最明显。
综上,单因素计算结果表明:缓冲结构的长度为60 m,截面积为140 m2,开孔率为40%时,初始压缩波的最大压力值和最大压力梯度值都能得到最大降低。
4. 多因素计算结果与分析
单因素计算结果,很好地反映了单个结构参数对压缩波的最大压力值和最大压力梯度值的影响。但是,缓冲结构对隧道入口效应减缓作用是由缓冲结构综合参数所决定的。因此,需要设计多因素的计算模型来综合考察缓冲结构对隧道入口效应的影响。
4.1. 构建模型及检验
根据单因素计算结果选取了各因素的四个值,构建计算方案,分析缓冲结构参数对压力值和压力梯度值的影响,其计算结果如表1所示。
 (a)
(a) 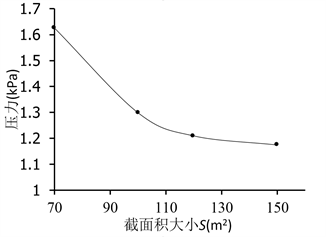 (b)
(b)
Figure 7. Effect of the sectional area of entrance hood
图7. 缓冲结构截面积的影响。(a) 压力值;(b) 压力梯度值
Table 1. Calculation plan and calculation results
表1. 计算方案与计算结果
根据计算结果,采用二次多项式进行拟合,得到回归方程R1和R2,R1为最大压力梯度值,R2为最大压力值。
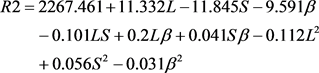
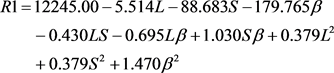
为了分析回归方程模型R、各个因素以及各因素间的交互作用项对目标值(压力值和压力梯度值)的显著性影响,本文通过方差分析计算了统计量F值,由于F值服从F分布,根据F分布函数可得到无显著影响的概率值(Pr > F),如表2所示,Pr > F值< 0.05视为有显著性影响 [15] 。回归方程模型R的Pr > F值 < 0.05表明回归方程拟合精度好,可以利用该近似模型进行后续的优化设计。
为了对回归方程进行误差统计分析 [16] ,对多元相关系数、可信度、精确度、精密度进行了计算,结果如表3和表4所示。多元相关系数R2越大,说明相关性越好;校正决定系数 与预测决定系数
与预测决定系数 这两个值较高且相差不大
这两个值较高且相差不大 ,说明回归方程能够充分模拟各因素对压力峰值和压力梯度值的影响;变异系数小于10%,表明仿真计算模型的可信度和精确度高;精密度是有效信号与噪声的比值,精密度大于4视为合理。从表3和表4可以看出,拟合的回归方程R1和R2符合以上检验原则,即适应性较好,可用来分析长度L、截面积S、开孔率β三因素对压力峰值和压力梯度值的相互影响。
,说明回归方程能够充分模拟各因素对压力峰值和压力梯度值的影响;变异系数小于10%,表明仿真计算模型的可信度和精确度高;精密度是有效信号与噪声的比值,精密度大于4视为合理。从表3和表4可以看出,拟合的回归方程R1和R2符合以上检验原则,即适应性较好,可用来分析长度L、截面积S、开孔率β三因素对压力峰值和压力梯度值的相互影响。
4.2. 各因素对压力梯度值的交互影响
基于前述多因素回归方程R1,分析单个因素固定不变时,其他两个因素的交互作用对最大压力梯度值的影响。各因素间交互作用的三维立体响应曲面如图8~图10所示,在被研究的区域内,当开孔率β固定不变时,缓冲结构长度L越长,截面积S较小(100 m2~120 m2)时,隧道内压缩波的压力梯度值较小;当截面积S固定不变时,缓冲结构长度L越长,开孔率β在35%~50%时,压力梯度值较小;当长度L固定不变时,截面积S较小(100 m2~120 m2),开孔率β在30%左右时,压力梯度值较小。
根据二次方程模型R1,可得到最优缓冲结构参数(压力梯度峰值最小时):L = 118 m,S = 120 m2,β = 47%,此时隧道内压缩波的压力梯度峰值最小,其值为2351 (Pa/s)。为验证方程计算结果,建立了最优缓
Table 2. Significant test of regression equations
表2. 回归方程的显著性检验

Figure 8. The interaction on pressure gradient of L and S
图8. L与S对压力梯度值的交互影响
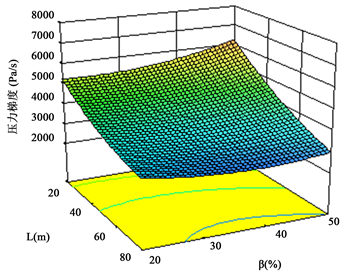
Figure 9. The interaction on pressure gradient of L and β
图9. L与β对压力梯度值的交互影响

Figure 10. The interaction on pressure gradient of S and β
图10. S与β对压力梯度值的交互影响
冲结构参数的隧道模型进行数值计算,得到压力梯度峰值为2131 (Pa/s),与方程模型预测值之间的误差率为9%。尽管最优结构参数确实使压力梯度值最小,但缓冲结构长度太长,考虑建造成本选取L = 80 m,S = 120 m2,β = 40%的参数也可以得到较小的压力梯度,而且只比最优参数下的压力梯度值大3%。
4.3. 各因素对最大正压值的交互影响
基于多因素回归方程R2,分析单个因素固定不变时,其他两个因素的交互作用对最大压力值的影响。从图11、12、13可以看出:在研究范围内(L = 20~80 m;S = 100~140 m2;β = 20%~50%),当缓冲结构越长,截面积越大,开孔率越小时,隧道内最大正压值也越小,说明增加缓冲结构长度和截面积可以有效缓解最大正压,而隧道开孔不利于降低隧道最大正压。所以在研究范围内最大正压最小时所对应的缓冲结构参数是L = 80 m,S = 140 m2,β = 20%。
Table 3. Statistical analysis of errors in the equation R1
表3. 回归方程R1误差统计分析
Table 4. Statistical analysis of errors in the equation R2
表4. 回归方程R2误差统计分析

Figure 11. The interaction on pressure of L and S
图11. L与S对压力值的交互影响

Figure 12. The interaction on pressure of L and β
图12. L与β对压力值的交互影响

Figure 13. The interaction on pressure of S and β
图13. S与β对压力值的交互影响
5. 结论
采用计算流体力学三维动态仿真的计算方法,基于粘性可压缩两方程紊流模型,研究了高速铁路单线隧道缓冲结构参数对初始压缩波的最大压力值和最大压力梯度的影响,得到结论如下:
1) 缓冲结构各参数对压缩波的最大压力梯度值的交互影响十分明显。通过缓冲结构的多参数综合优化得到:缓冲结构的长度为80 m,截面积为120 m2,开孔率为40%时,最大压力梯度值能得到最有效降低。
2) 增加缓冲结构长度和截面积可以有效缓解最大正压值,而隧道开孔不利于降低最大正压值。在本文研究范围内,最大正压最小时所对应的缓冲结构长度为80 m,截面积为140 m2,开孔率为20%。
3) 由于微气压波强度正比于隧道出口处压缩波压力梯度最大值,即微气压波强度主要受压力梯度大小的影响,所以优化缓冲结构参数时主要考虑压力梯度值的变化。综合考虑,本文计算模型所得到的单线隧道最优缓冲结构为:长度为80 m,截面积为120 m2,开孔率为40%。
基金项目
国家自然科学基金(51475387)。
文章引用
杨 军,李人宪. 单线隧道缓冲结构参数的优化
Optimization of Structural Parameters of the Single-Line Tunnel Entrance Hood[J]. 交通技术, 2018, 07(03): 129-139. https://doi.org/10.12677/OJTT.2018.73016
参考文献
- 1. Ozawa, S. (1979) Studies of Micro-Pressure Wave Radiated from a Tunnel Exit. RTRI Report, 1121, 1-92.
- 2. Yamamoto, A. (1977) Micro-Pressure Wave Radiated from Tunnel Exit. Preprint of Spring Meeting of Physical Society of Japan, Japan.
- 3. 骆建军, 姬海东. 高速列车进入有缓冲结构隧道的压力变化研究[J]. 铁道学报, 2011, 33(9): 114-118.
- 4. 骆建军, 王梦恕, 高波, 等. 高速列车进入带缓冲结构隧道的压力变化研究(I) [J]. 空气动力学学报, 2007, 25(4): 488-494.
- 5. 骆建军, 高波, 王英学. 高速列车突入隧道与缓冲结构时的数值模拟[J]. 空气动力学学报, 2003, 21(3): 376-381.
- 6. 骆建军, 马伟斌. 高速铁路长隧道内缓冲结构的气动效应分析[J]. 中国铁道科学, 2016, 37(2): 48-55.
- 7. 王英学, 高波, 赵文成, 等. 缓冲结构对列车突入隧道时的瞬变压力的影响[J]. 铁道工程学报, 2004, 21(1): 94-98.
- 8. 闫亚光, 杨庆山, 骆建军. 缓冲结构对隧道气动效应减缓效果[J]. 北京交通大学学报, 2013, 37(4): 7-12.
- 9. Ozawa, S. and Maeda, T. (1988) Tunnel Entrance Hoods for Reduction of Micro-Pressure Wave. Quarterly Report of Railway Technical Research Institutes, 29, 134-139.
- 10. Vardy, A.E. (1975) Ventilated Approach Regions for Railway Tunnels. Transportation Engineering Journal of the American Society of Civil Engineers, 101, 609-619.
- 11. 李人宪. 高速列车气动影响[M]. 北京: 中国铁道出版社, 2016.
- 12. 李人宪. 有限体积法基础(第2版) [M]. 北京: 国防工业出版社, 2008.
- 13. CD Adapoo Group. User Guide of Star-CD Version 3.22. CD Adapoo Group, London, 403-430.
- 14. Howe, M.S. (1999) On the Compression Wave Generated When a High-Speed Train Enters a Tunnel with a Flared Portal. Journal of Fluids & Structures, 13, 481-498. https://doi.org/10.1006/jfls.1999.0217
- 15. 葛宜元. 试验设计方法与Design-Expert软件应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
- 16. 李莉, 张赛, 何强, 等. 响应面法在试验设计与优化中的应用[J]. 实验室研究与探索, 2015, 34(8): 41-45.
