Open Journal of Circuits and Systems
Vol.05 No.01(2016), Article ID:17165,11
pages
10.12677/OJCS.2016.51002
A New Five Dimensional Hyper-Chaotic Circuit and Its Application in Secure Communication
Zhichao Long, Dazhu Ma
School of Science, Hubei University for Nationalities, Enshi Hubei

Received: Feb. 29th, 2016; accepted: Mar. 15th, 2016; published: Mar. 18th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The dynamic behavior of a hyper-chaotic system is much more difficult to be predicted than that of a normal chaos system. Therefore, it becomes very useful in the secure communication. This paper constructed a new five dimensional hyper-chaotic circuit based on Chen system when the two state variables and an inverse controller are introduced. First, the stability of the fixed points and dynamic behavior of the phase space of the new system are discussed, and three positive Lyapunov exponents are found. Modular circuit of the system is designed. The results of circuit simulation are in agreement with the numerical simulation. Then chaos synchronism of the system is achieved with drive-response synchronization method. Numerical simulation of the secure communication process for the square wave signal is given, and chaotic masking method is used to realize the secure communication circuit with square wave voltage signal of the system. Finally, two ways to deal with secure communication are discussed; one is the chaotic signal mixed with the image, and the other is chaotic signal added to the digital image. It is shown that the latter is better than the former in the effect on secure communication, and is more suitable for information reversion.
Keywords:Chaotic Circuit, Hyperchaos, Lyapunov Exponent, Secure Communication

一个新五维超混沌电路及其在保密通讯中应用
龙志超,马大柱
湖北民族学院理学院,湖北 恩施

收稿日期:2016年2月29日;录用日期:2016年3月15日;发布日期:2016年3月18日

摘 要
超混沌系统比普通混沌系统的动态行为更加难以预测,因此在保密通讯中具有更重要的应用价值。本文在Chen混沌系统中引入两个状态变量和一个反向控制器构造了一个新的五维超混沌系统。首先讨论了新系统的定点稳定性及其相空间动力学行为,发现新系统有3个正的Lyapunov指数。设计了该系统的模块化电路,示波器观测结果与数值模拟结果一致。其次采用驱动响应式同步方式实现了新系统的混沌同步,并数值模拟了方波信号的混沌保密通讯过程,利用混沌掩盖法完成了新系统方波信号的混沌保密通讯电路。最后,分别采用混沌信号加入到图片中和图片数字化加入到混沌信号中两种不同的方式实现图片的混沌保密通讯过程。对比研究表明后者的加密效果更好,具有更高的信息还原度。
关键词 :混沌电路,超混沌,Lyapunov指数,保密通讯

1. 引言
混沌是在确定性非线性系统中发生的不可预测后期演化的现象 [1] 。自《周期3意味着混沌》 [2] 一文给出混沌的数学定义之后,混沌理论得到极大发展。在牛顿天体力学和广义相对论等领域有许多讨论混沌的文章 [3] - [12] 。目前比较成熟的混沌识别方法有庞加莱截面、李雅普诺夫指数、快速李雅普诺夫指数、较小排列指数、频谱分析等方法 [3] - [14] 。庞加莱截面法可直观反映系统的动力学性质,但最适宜不超过四维的保守系统;李雅普诺夫指数是衡量两邻近轨道随时间平均分离比的指标,也能够区别混沌和超混沌现象,有变分法和两粒子法两种方式,有时候两者可以结合使用;相比李雅普诺夫指数,快速李雅普诺夫指数在给定的时间内不采用重整化,也不对时间平均,能迅速区分有序和混沌轨道,但不能区分混沌和超混沌现象;较小排列指标是利用积分运动方程和同时积分两次变分方程得到的,其和频谱分析等方法一样都是保守系统中常用的混沌识别方法。本文采用Benettin [14] 等人提出的计算李雅普诺夫指数方法。
混沌理论和各种识别方法也可以应用到实际工程领域,混沌控制与同步就是其中一个重要的研究方向 [15] - [18] ,研究人员一方面设计了多个混沌控制与同步的方法,另一方面关注混沌电路在保密通讯方面的应用。超混沌系统比普通混沌系统具有更为复杂的动力学行为,含有两个或两个以上正的Lyapunov指数 [19] 。加入复杂的超混沌信号可以提高混沌保密通信和混沌信息加密的安全性,并且超混沌电路系统一般具有强大的储容量和信息处理能力以及鲁棒性等优点,因此超混沌电路具有重要的研究价值 [20] [21] 。构造超混沌系统的方法也一直在逐步形成和发展。超混沌Rössler系统 [22] 和超混沌Chua系统 [23] 最早出现的高维超混沌系统。近年来通过在连续混沌系统中加入反馈控制器得到超混沌的方法得到关注 [24] - [29] 。加入反馈控制可以控制系统的定点个数、定点稳定性、耗散性等,从而确定一个系统处于超混沌状态时的参数范围。文献中已通过该方法可以分别将Lorenz系统 [30] 、改进的Chen系统 [31] 和Lu系统 [32] 控制为超混沌系统。本文在Chen混沌系统 [33] 中加入两个控制器,也可将其控制到超混沌状态,通过理论分析、Lyapunov指数、数值模拟和电路实验验证了其超混沌特性,并在此基础上实现了新系统的混沌同步与保密通讯。
2. 控制Chen系统到五维超混沌系统
2.1. 模型
Chen系统 [33] 的状态方程为:
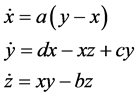 (1)
(1)
取参数a = 35,b = 3,c = 28时,Chen系统处于混沌状态。本文在Chen系统中加入第四个方程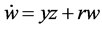 和第五个方程
和第五个方程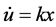 ,第三个方程加上反向控制器−ku。得到一个新五维非线性系统:
,第三个方程加上反向控制器−ku。得到一个新五维非线性系统:
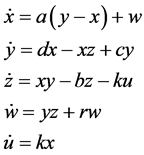 (2)
(2)
参数a,b,c,d,k为变量,令a = 35,b = 5,c = 12,d = 5,r =0.5,k = 1.5,采用四阶龙格库塔法对系统数值模拟,可得系统的相位图如图1所示,其中三个平面均含有双涡卷结构,u-z平面结构更为复杂。
2.2. 系统基本特性
2.2.1. 定点稳定性
这里采用李雅普诺夫第一法,在定点的领域把非线性方程线性化,利用线性化方程的解可得定点的稳定性。由方程(2),可得新系统只存在唯一定点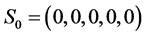 ,在平动点附近的线性化Jacobian矩阵为:
,在平动点附近的线性化Jacobian矩阵为:
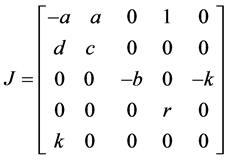 (3)
(3)
设特征值为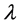 ,E为单位矩阵,则特征方程为
,E为单位矩阵,则特征方程为
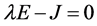 (4)
(4)
当参数a = 35,b = 5,c = 12,d = 5,r =0.5,k = 1.5时,代入可得
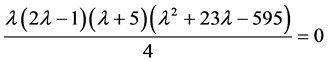 (5)
(5)
特征值为
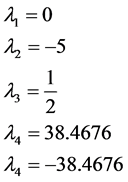 (6)
(6)
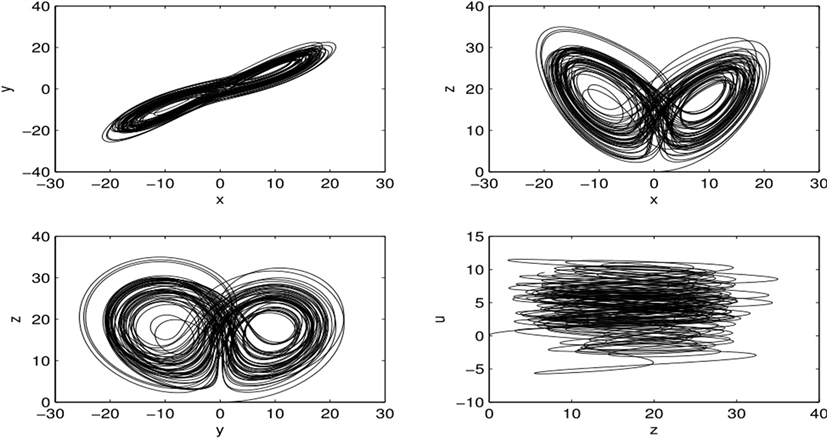
Figure 1. Phase space structure
图1. 相空间结构图
特征值有一个为零,两个为负,两个为正数,和文献 [27] 中超混沌模型定点处的稳定性情况一样。
2.2.2. 相体积
系统(2)的散度为
 (7)
(7)
当取参数a = 35,b = 5,c = 12,r =0.5时,有
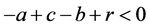 (8)
(8)
在上述参数条件下,系统散度小于0,说明此时系统处于耗散状态,该系统为耗散系统。
2.2.3. 李雅普诺夫指数
李雅普诺夫指数是衡量两邻近轨道随时间平均分离比的指标,是研究混沌行为的一个重要工具。本文采用Benettin 等人在1980年给出的计算李雅普诺夫指数的方法,每积分一次都进行一次Gram-Schmidt正交归一化。如果系统含有1个大于零的李雅普诺夫指数,则该系统为混沌系统;如果含有2个或者2个以上正的李雅普诺夫指数,则系统为超混沌系统。新系统含有3个非线性项和5个李雅普诺夫指数。以四阶龙格库塔为基本数值工具,给定参数a = 35,b = 5,c = 12,d = 5,r =0.5,k = 1.5,系统的李雅普诺夫指数如图2所示。5个李雅普诺夫指数中有3个为正,1个为零,1个为负,说明新系统在满足上述条件时处于超混沌状态。在系统相空间结构图1中出现的3个双涡卷结构,与系统含有3个正的李雅普诺夫指数是一致的。
3. 五维超混沌系统的电路实验
为了从物理上说明该系统的混沌特性,我们利用改进型模块化方法设计系统的模拟电路。电路部分一般由四个模块组成,即反向器模块、反相积分器模块、反相加法比例运算模块和函数发生器模块。本文设计过程只需其中的三个模块。
运算放大器的端电压最大为35 v,有必要对系统(2)作变量比例压缩变换。设压缩系数为n = 5,则
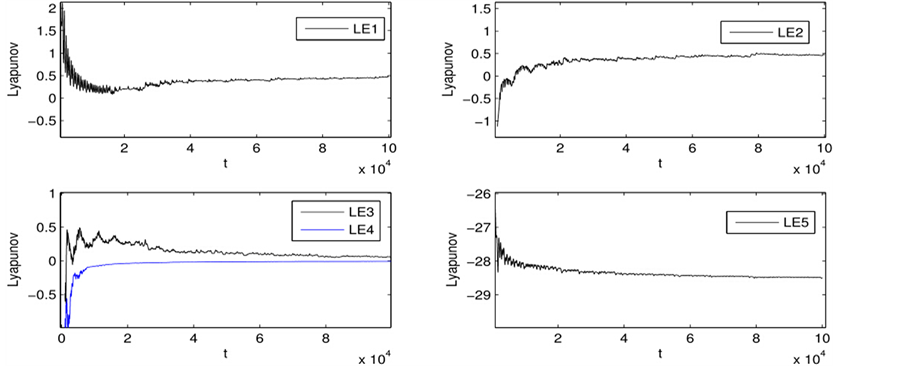
Figure 2. Lyapunov exponents of the system
图2. 系统Lyapunov指数
nx → x,ny → y,nz → z,nw → w,nu → u,压缩方程为:
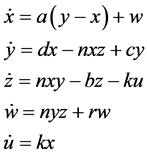 (9)
(9)
还需作时间上的尺度变换,设尺度因子为100,则对应的微积分转换为:
 (10)
(10)
模拟电路由反向比例积分器、反相器和电子器件乘法器构成,可以实现系统中的加、减、乘和积分运算。本文的运算放大器为TL085,乘法器选用AD633,电源电压为±35 v。系统(9)对应的改进型模块化设计电路如图3所示。
电路图中R5 = 28.75 kΩ、R4 = 28.75 kΩ,与之对应的系统中的参数为a = 35;R10 = 666.67 kΩ、R1 = 666.67 kΩ,其对应参数为k = 1.2;R7 = 200 kΩ、R8 = 83.333 kΩ、R11 = 200 kΩ、R14 = 2000 kΩ对应的参数分别为d = 5、c = 12、b = 5、r = 0.5。其它参数在图3中均有标注。采用Multism 12仿真电路,在示波器上得到相空间在各相平面上的投影图。图4和图5分别对应图1的上方和下方两图,在噪声干扰最少时,电路仿真和数值模拟的结果完全符合,从而在物理上说明新系统的超混沌特性。
4. 系统在保密通讯中的应用探究
4.1. 混沌同步
混沌同步是混沌保密通讯的应用基础。实现混沌同步方法有驱动响应式同步、耦合同步、自适应同步、脉冲同步等。其中驱动–相应式同步的特点是两个非线性动力系统存在着驱动与响应的关系,响应系统行为
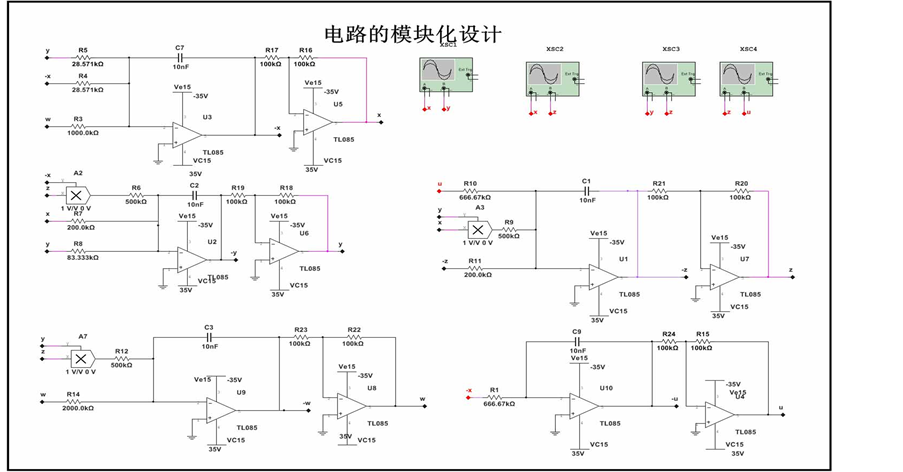
Figure 3. 5D hyperchaos circuit diagram
图3. 五维超混沌电路图

Figure 4. Circuit simulation results. The left refers x-y plane, the right refers x-z plane
图4. 电路仿真图。左边为x-y平面,右边是x-z平面

Figure 5. Circuit simulation results. The left is y-z plane, the right is the z-u plane
图5. 电路仿真图,左边对应y-z平面,右边为z-u平面
取决于驱动系统,驱动系统的行为与响应系统无关。该方法只需要通过信道传送一路加密信号,并且是自同步方式,当系统由于某种原因失步后能重新自动同步,与现有通讯传送方式兼容。本文采用驱动响应式同步。
用变量x(1)作为驱动变量,驱动系统的状态方程为
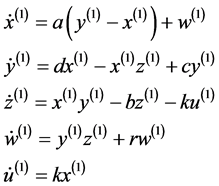 (11)
(11)
当变量x (1)为驱动信号,同步步系统的状态方程为
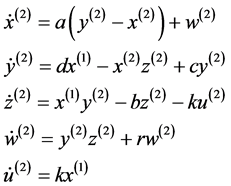 (12)
(12)
虽然响应系统和驱动系统具有相同的形式,但是(12)式中用驱动系统中的混沌信号x(1)取代原系统的部分混沌信号x(2)。驱动系统和同步系统误差为ex = x(1) − x(2),ey = y(1) − y(2),ez = z(1) − z(2),ew= w(1) − w(2),eu = u(1) − u(2)。令驱动系统的初始条件为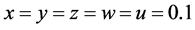 ,同步系统的初始条件为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,即驱动系统和同步系统处于不同步的状态。数值模拟得到误差ex,ey,ez,ew随时间的变化如图6所示。
,同步系统的初始条件为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,即驱动系统和同步系统处于不同步的状态。数值模拟得到误差ex,ey,ez,ew随时间的变化如图6所示。
虽然驱动系统和同步系统的初始状态相差较大,两系统处于完全不同步状态,但是通过同步的控制,误差很快变小,达到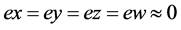 状态。说明系统快速达到稳定混沌同步,确实能够满足保密通讯的要求。
状态。说明系统快速达到稳定混沌同步,确实能够满足保密通讯的要求。
4.2. 保密通讯数值模拟
此处我们模拟了图片的加密传输和方波信号两种保密通讯方式,方波信号可以代表实际通讯中的数值信号。首先,Matlab模拟方波信号的混沌保密通讯,驱动系统的初值为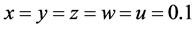 ,同步系统的初始值为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,其结果如图7所示:s,s1,s2分别是加密前、加密后、解密后的信号图像。当系统达到混沌同步后,解密后的信号和原信号相比,失真度不大,说明该保密通讯方案是合理的。
,同步系统的初始值为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,其结果如图7所示:s,s1,s2分别是加密前、加密后、解密后的信号图像。当系统达到混沌同步后,解密后的信号和原信号相比,失真度不大,说明该保密通讯方案是合理的。
其次模拟图片混沌保密通讯过程。驱动系统混沌信号对每个像素点的RGB颜色值分别进行位运算,形成加密图片,接受端接收到加密图片后,用同步系统对应的混沌信号对已加密图片位运算解密。仿真结果见图8,从左至右分别为发送前图片、混沌加密后传输途中图片和接收端解密后图片。虽然加密效果良好,但是图片解密后失真的情况比较严重。最右图的上半部分,解密后处于不清晰状态,这是由于系统还没有达到混沌同步。但是当混沌达到同步后,图片仍有较为严重的失真情况,噪点比较明显。因此,该方案不适合图片的混沌加密传输。其原因在于加密系统和解密系统存在误差,使得该加密方式失真度大。
由于混沌同步的误差是无法消除的,因此我们采用另外一种混沌加密方式。图7中输入信号和输出信号之间存在一定误差,但如果把方波波形看成数字信号,若方波电压为1代表1,为−1的时候代表0,那么输入信号和输出信号所代表的信息就完全一样了。基于此,我们首先把图片的每个像素点的三个值由十进制化为二进制,电路中将二进制数字信号转化为电信号。数值模拟时需将图片转换的二进制数据整理成适用于混沌加密和解密的数据,像素的最大值为255,转化为二进制后刚好为8位。按照每8个位值存放一个数据的方式建立数组,将图片存放在数组中。利用混沌掩盖方法将数组中的数据混合到混沌信号中,接收端得到混入图片信息的混沌信号,混沌同步后解密。由于存在误差,需要对信号处理,将数据重新变为0和1的形式,最后将二进制数据还原为十进值数据,确定好数据对应位置,就可以还原图片了。该加密方式可以减小混沌同步固有误差的影响,加密效果好,数据还原度高,该方法还可以推广到其它形式的数据传播中。传播图中为混沌模拟信号,该信号并不是图片信息,如果按照图片信息处理的话,将完全是黑色,此时解密出图片信息的难度较大。数值模拟见图9,从左到右分别为图片加密前、加密后图像信号和解密后的图片。当系统达到混沌同步后,该方式有很好的加密效果,而且解密后图片的失真度很小。由此可见,该方案具有实际工程应用价值。
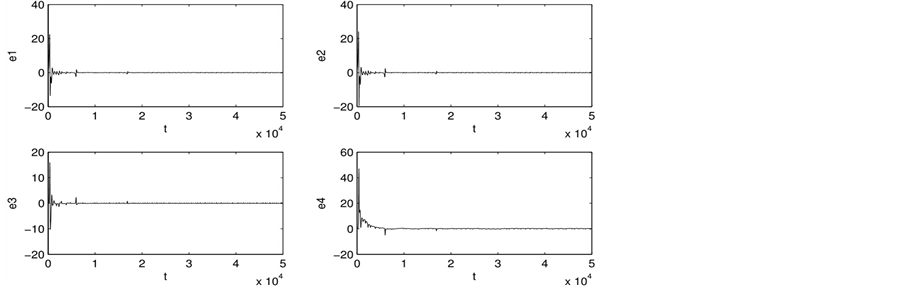
Figure 6. Errors over with time
图6. 误差随时间变化图
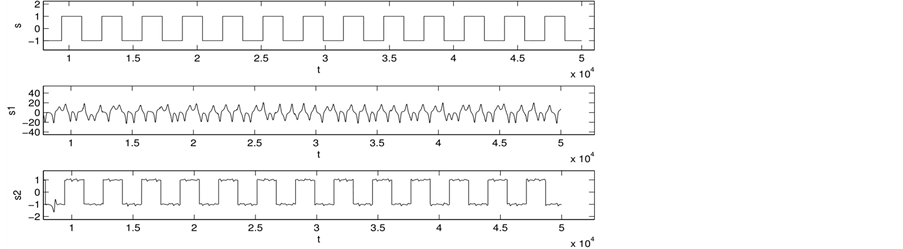
Figure 7. Numerical simulation results of square wave type signal
图7. 方波信号混沌保密通讯数值模拟结果图

Figure 8. Encryption and decryption of chaos signal mixed with image
图8. 混沌信号加入图片的加密和解密图

Figure 9. Encryption and decryption of chaos signal mixed with digital image
图9. 图片数字化后加入混沌信号的加密和解密图
4.3. 保密通讯电路实现
基于驱动–响应式同步,直接采用混沌掩盖法实现其混沌保密通讯。超混沌电路系统的驱动–响应式同步保密通信方案的完整电路图如图10所示。p=x(1)+s为加密信号,其中s为信号发生器。S2为解密信号,这里s2 = x(2) − p。数值模拟时设S0 = sin(0.01t),驱动系统的初值为 ,同步系统的初始值为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,结果如图11所示。图中当系统达到混沌同步后,
,同步系统的初始值为x = 3,y = 1,z = 0.2,w = 0.2,u = 0.3,结果如图11所示。图中当系统达到混沌同步后,
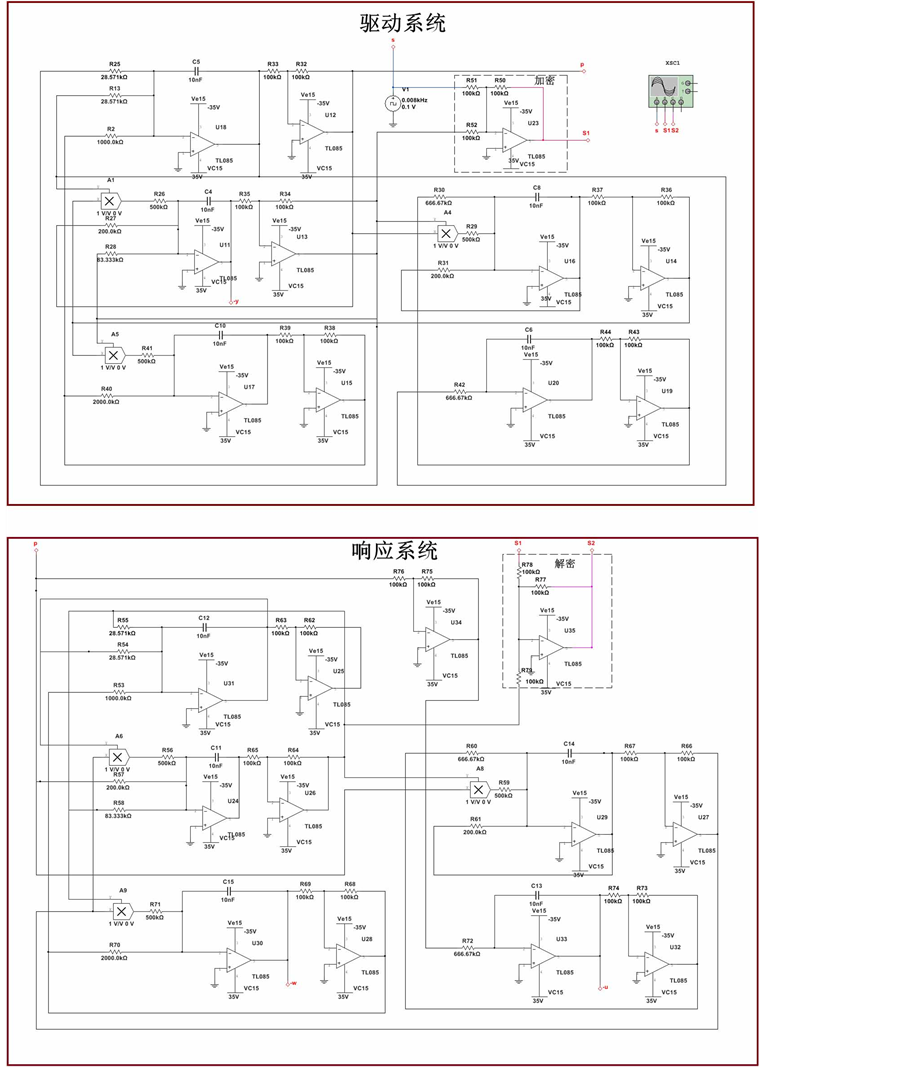
Figure 10. The principle diagram of the chaotic secret communication
图10. 混沌保密通讯电路原理图
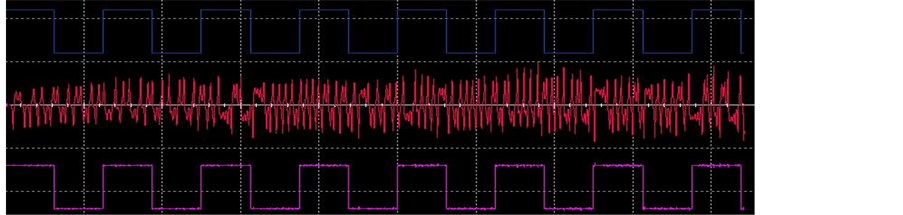
Figure 11. Circuit simulation results of square wave type signal
图11. 方波信号的混沌保密通讯电路结果图
解密后的信号和原信号相比,失真度不大。若输入信号S = 0.1 V,频率为8 Hz,电路仿真结果如图11所示。从上到下依次为示波器给出的加密前、加密后、和解密后的电压信号随时间变化图。电路仿真结果与数值模拟结果图7基本一致,说明新混沌电路系统成功完成了对一个方波电压信号的加密和解密过程。
5. 结论
在Chen系统引入反馈控制器方法构造了一个新五维超混沌系统,该系统存在唯一平动点,分析了定点稳定性和系统相体积,确定了系统处于耗散状态时的参数。在给定参数区域内系统具有3个正的Lyapunov指数, 说明系统处于超混沌状态。电路的仿真结果和数值模拟结果具有高度一致性,从物理上说明了系统的超混沌行为。数值模拟了系统的混沌同步过程,给出了误差随时间的变化情况,结果表明,驱动系统和响应系统可以快速达到混沌同步,达到了保密通讯的基本要求。数值模拟了系统对方波信号的保密通讯过程以及对图片信息的两种混沌加密方案,得出图片数字化后加入混沌信号的方式效果更好。最后基于混沌掩盖法设计了五维超混沌系统的驱动-响应式同步保密通信电路。
基金项目
本文受国家自然科学基金项目(11263003)和湖北民族学院教研项目(2014JY030)资助。
文章引用
龙志超,马大柱. 一个新五维超混沌电路及其在保密通讯中应用
A New Five Dimensional Hyper-Chaotic Circuit and Its Application in Secure Communication[J]. 电路与系统, 2016, 05(01): 10-20. http://dx.doi.org/10.12677/OJCS.2016.51002
参考文献 (References)
- 1. 刘崇新. 分数阶混沌电路及应用[M]. 西安: 西安交通大学出版社, 2011: 1-20.
- 2. Li, T.Y. and Yorke, J.A. (1975) Period Three Implies Chaos. American Mathematical Monthly, 82, 985-992. http://dx.doi.org/10.2307/2318254
- 3. Wu, X., Huang, T.Y and Zhang, H. (2006) Lyapunov Indices with Two Nearby Trajectories in a Curved Spacetime. Physical Review D, 74, Article ID: 083001. http://dx.doi.org/10.1103/PhysRevD.74.083001
- 4. Wu, X. and Xie, Y. (2007) Revisit on “Ruling Out Chaos in Compact Binary Systems”. Physical Review D, 76, Article ID: 124004. http://dx.doi.org/10.1103/PhysRevD.76.124004
- 5. Wu, X. and Xie, Y. (2008) Resurvey of Order and Chaos in Spinning Compact Binaries. Physical Review D, 77, Article ID: 103012. http://dx.doi.org/10.1103/PhysRevD.77.103012
- 6. Huang, G., Ni, X. and Wu, X. (2014) Chaos in Two Black Holes with Next-to-Leading Order Spin-Spin Interactions. The European Physical Journal C, 74, 1-8. http://dx.doi.org/10.1140/epjc/s10052-014-3012-2
- 7. Huang, G. and Wu, X. (2014) Dynamics of the Post-Newtonian Circular Restricted Three-Body Problem with Compact Objects. Physical Review D, 89, Article ID: 124034. http://dx.doi.org/10.1103/PhysRevD.89.124034
- 8. Wu, X., Mei, L. and Huang, G. (2015) Analytical and Numerical Studies on Differences between Lagrangian and Hamiltonian Approaches at the Same Post-Newtonian Order. Physical Review D, 91, Article ID: 024042. http://dx.doi.org/10.1103/physrevd.91.024042
- 9. Mei, L., Ju, M. and Wu, X. (2013) Dynamics of Spin Effects of Compact Binaries. Monthly Notices of the Royal Astronomical Society, 435, 2246-2255. http://dx.doi.org/10.1093/mnras/stt1441
- 10. Wu, X. and Huang, G. (2015) Ruling out Chaos in Comparable Mass Compact Binary Systems with One Body Spinning. Monthly Notices of the Royal Astronomical Society, 452, 3167-3178. http://dx.doi.org/10.1093/mnras/stv1485
- 11. Wu, X. and Huang, T. (2003) Computation of Lyapunov Exponents in General Relativity. Physics Letters A, 313, 77-81. http://dx.doi.org/10.1016/S0375-9601(03)00720-5
- 12. 伍歆, 黄天衣. 判定轨道混沌的几个指标[J]. 天文学进展, 2006, 23(4): 318-330.
- 13. Benettin, G., Galgani, L. and Giorgilli, A. (1980) Lyapunov Characteristic Exponents for Smooth Dynamical Systems and for Hamiltonian Systems; A Method for Computing All of Them. Part 1: Theory. Meccanica, 15, 9-20. http://dx.doi.org/10.1007/bf02128236
- 14. Froeschle, C., Lega, E. and Gonczi, R. (1997) Fast Lyapunov Indicators. Application to Asteroidal Motion. Celestial Mechanics and Dynamical Astronomy, 67, 41-62. http://dx.doi.org/10.1023/A:1008276418601
- 15. Ott, E., Grebogi, C. and Yorke, J.A. (1990) Controlling Chaos. Physical Review Letters, 64, 1196-1199. http://dx.doi.org/10.1103/PhysRevLett.64.1196
- 16. Hübler, A. (1998) Adaptive Control of Chaotic Systems with Uncertainties. International Journal of Bifurcation & Chaos, 8, 2041-2046. http://dx.doi.org/10.1142/S0218127498001698
- 17. 余思敏. 混沌系统与混沌电路原理设计及其在通讯中的应用[M]. 西安: 西安电子科技大学出版社, 2011: 4-50.
- 18. Huang, G.Q. and Wu, X. (2012) Analysis of New Four-Dimensional Chaotic Circuits with Experimental and Numerical Methods. International Journal of Bifurcation and Chaos, 22, 1250042-1250055. http://dx.doi.org/10.1142/S0218127412500423
- 19. Luo, X.S., Fang, J.Q. and Wang, L.H. (1999) A New Strategy of Chaos Control and a United Mechanism for Several Kinds of Chaos Control Methods. Acta Physica Sinica, 8, 895-901.
- 20. Boccaletti, S., Grebogi, C., Lai, Y., Mancini, H. and Maza, D. (2000) The Control of Chaos: Theory and Applications. Physics Reports, 329, 103-197. http://dx.doi.org/10.1016/S0370-1573(99)00096-4
- 21. Rössler, O.E. (1979) An Equation for Hyperchaos. Physics Letters A, 71, 155-157. http://dx.doi.org/10.1016/0375-9601(79)90150-6
- 22. Thamilmaran, K., Lakshmanan, M. and Venkatesan, A. (2004) A Hyperchaos in a Modified Canonical Chua’s Circuit. International Journal of Bifurcation and Chaos, 14, 221-243. http://dx.doi.org/10.1142/S0218127404009119
- 23. Yeh, K., Chen, C.W. and Hsiwng, T.K. (2005) Fuzzy Control for Seismically Excited Bridges with Sliding Bearing Isolation. Advanced Intelligent Computing Theories and Applications, 4681, 473-483.
- 24. Edward, O. (1993) Chaos in Dynamical Systems. Cambridge University Press, Cambridge.
- 25. 谌龙, 彭海军, 王德石. 一类多涡卷混沌系统构造方法研究[J]. 物理学报, 2008, 57(6): 3337-3341.
- 26. Chen, G., Moiola, J.L. and Wanf, H.O. ( 2000) Bifurcation Control: Theories, Methods, and Applica-tions. International Journal of Bifurcation and Chaos, 10, 511-548. http://dx.doi.org/10.1142/S0218127400000360
- 27. 王光义, 郑艳, 刘敬彪. 一个超混沌Lorenz吸引子及其电路实现[J]. 物理学报, 2007(6): 3113-08.
- 28. Chen, G. and Ueta, T. (1999) Yet Another Chaotic Attractor. Interna-tional Journal of Bifurcation and Chaos, 9, 1465- 1466. http://dx.doi.org/10.1142/S0218127499001024
- 29. Li, Y., Tang, W.K.S. and Chen, G. (2005) Hyperchaos Evolved from the Generalized Lorenz Equation. International Journal of Circuit Theory and Applications, 33, 234-251. http://dx.doi.org/10.1002/cta.318
- 30. Li, Y.X., Tang, W.K.S. and Chen, G.R. (2005) Generating Hyper-Chaos via State Feedback Control. International Journal of Bifurcation and Chaos, 15, 3367-3375. http://dx.doi.org/10.1142/S0218127405013988
- 31. Chen, A., Lu, J., Lü, J. and Yu, S. (2006) Generating hyperchaotic Lü attractor via state feedback control. Physica A, 364, 103-110. http://dx.doi.org/10.1016/j.physa.2005.09.039
- 32. Wang, G., Zhang, X., Zheng, Y. and Li, Y. (2006) A new modified hyperchaotic Lü system. Physica A, 371, 260-272. http://dx.doi.org/10.1016/j.physa.2006.03.048
- 33. Wang, B. and Guan, Z.H. (2010) Chaos Synchronization in General Complex Dynamical Networks with Coupling Delays. Nonlinear Analysis Real World Applications, 11, 1925-1932. http://dx.doi.org/10.1016/j.nonrwa.2009.04.020