Biophysics
Vol.06 No.03(2018), Article ID:26562,7
pages
10.12677/BIPHY.2018.63005
Spatio-Temporal Pattern in a Subnetwork of a Bi-Layer Neuronal Network
Yanhong Zheng
College of Mathematics and Informatics & FJKLMAA, Fujian Normal University, Fuzhou Fujian

Received: Jul. 31st, 2018; accepted: Aug. 15th, 2018; published: Aug. 23rd, 2018

ABSTRACT
The firing behaviour and spatio-temporal pattern of neurons in the ring subnetwork of a bi-layer neuronal network coupled by a ring network and a grid network are studied in this paper. For the ring subnetwork, the firing behaviour and the spatio-temporal pattern of neurons are mainly influenced by the interlayer coupling strength. The grid-layer network will influence the firing behaviour of the neurons in ring-layer network with the interlayer coupling strength increasing.
Keywords:Bi-Layer Neuronal Network, Firing Behaviour, Spatio-Temporal Pattern
双层神经元网络中子网络的时空斑图研究
郑艳红
福建师范大学,数学与信息学院&福建省分析数学及应用重点实验室,福建 福州

收稿日期:2018年7月31日;录用日期:2018年8月15日;发布日期:2018年8月23日

摘 要
本文研究环–格子耦合神经元网络中环式子网络的神经元放电行为和时空斑图演化,发现神经元的放电行为和时空斑图的演化主要受两个网络耦合强度的影响,随着层间耦合强度增大,格子网络会影响环式网络神经元的放电有序性。
关键词 :双层神经元网络,放电行为,时空斑图

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
人类大脑是一个大的系统,是数量巨大的神经元由突触连接,组成一个神经元网络,它在多重组织层次上运作的,每个层次都有其自身的时间和空间尺度 [1] 。脑皮层中不同层有神经元之间的连接,同一层内也有神经元之间的连接,所以实际的神经元系统非常复杂。为了理论研究的方便,可以将神经元系统看成一个由众多简单的神经元网络所组成庞大的复杂网络。因此,揭示神经元放电的机理,讨论集群神经网络与多层神经网络的动力学行为对理解和认识神经元系统的认知功能具有非常重要的理论意义,也对理解生物器官的功能及其运作机理有着不可忽视的参考价值。
许多学者对多层网络的同步问题进行研究。介观神经元网络的子神经元网络内与子神经元网络间的耦合强度都可以使其发生簇同步转迁 [2] ;对于介观的无标度神经元网络,可以通过对网络中某个hub节点的调控来调节介观神经元网络的簇放电同步性 [3] ;对于介观的小世界神经元网络,Batista等研究簇放电神经元的集群动力学,给出基于簇内和簇间连接概率的网络出现全局簇同步时耦合强度的临界值范围 [4] ;双层小世界神经元网络的同步斑图不仅与层间耦合强度有关,而且与各层网络的加边概率有关。此外,噪声会增强弱耦合双层神经元网络的斑图同步,但对强耦合双层神经元网络的同步并无显著影响 [5] 。由于神经元处在一个内外噪声共存的环境中,受到各种不同强度和不同形式的内部和外部的刺激,因而其输出具有一定的随机性 [6] 。对于噪声环境下两个格子耦合的神经元网络,当层间耦合强度增加时两层网络会达到同步,同步状态强依赖于层间耦合强度和该双层网络噪声强度的不同 [7] 。而对介观小世界神经元网络的随机共振现象研究发现噪声诱导的随机共振现象与子神经元网络内部的耦合强度、子神经元网络间的耦合强度、子神经元网络的小世界网络重连概率、子神经元网络的数目等密切相关 [8] 。此外,文献 [9] 借助对多层次神经元网络同步动力学特性的分析,阐述了大脑皮层的结构性网络与功能性网络之间的关联性。
本文主要研究噪声环境下由Morris-Lecar (ML)神经元 [10] 组成的环–格子耦合的双层网络中环式子网络的放电动力学行为,其中环式耦合神经元网络是N个具有类型I兴奋性的全同ML神经元通过环式耦合构成,格子耦合神经元网络是 个具有类型II兴奋性的全同ML神经元通过格子耦合构成。
2. 噪声环境下的环–格双层耦合网络模型
Morris-Lecar神经元模型是描述北极鹅肌肉纤维的电活动的一个神经元模型。这个模型能模拟现实神经元的激发和恢复的特性。模型包含了一个产生快的动作电位的一个Ca2+流和一个K+流。与此同时,为了维持休止态处的恒定电位,还考虑了一个漏电流。二维的ML神经元模型由下面的微分方程给出:
(1)
其中 和 满足
这里t是时间变量,V是神经元的膜电位,n是K+离子通道的活化概率。参数C, , , , , , , , , , , , , , ,I的意义参见文献 [10] ,这里取 , , , , , , , 。
此模型当调节外界电流强度时能够发现丰富的动力学行为。ML神经元是I型兴奋性还是II型兴奋性,取决于参数 和 的取值。当 , , , 时,神经元是I型兴奋性;当 , , , 时,神经元是II型兴奋性。
神经元有许多不同的连接方式,如链形,环形和全局连接,使它们能够执行不同的功能。此外,大多数的哺乳动物的神经元表现出的是类型I兴奋性,如锥体细胞在脑中被认为是类型I兴奋性的 [6] ,因此考察噪声对耦合的类型I兴奋性神经元和类型II兴奋性神经元的影响很重要。下面我们构造两个网络,一个是由N个全同的类型I兴奋性ML神经元电突触耦合构成的环式子网络A,即每个神经元只跟与它最邻近的两个神经元连接组成一个环;一个是由 个全同的类型II兴奋性ML神经元电突触耦合构成的格子子网络B,即每个神经元与它最邻近的神经元耗散耦合,形成一个格子网络。此外,网络A的第i个神经元与网络B的对角线上第ii个神经元电耦合,这种耦合意味着A和B的神经元之间电突触的相互作用。
噪声环境下与格子网络B耦合的环式网络A的动力学方程如下:
(2)
其中
这里下标i指第i个神经元,其中 。参数 , , , 这表明网络A中的神经元是类型I兴奋性,电流 表明无噪声环境下每个神经元未耦合前都处于周期1放电状态。 是加在第i个神经元上的高斯白噪声,它满足 , ,D表示噪声强度,g1是网络A的内部耦合强度,g3是网络间层与层的耦合强度。
噪声环境下与环式网络A耦合的格子网络B的时空演化由下面方程描述:
(3)
其中
这里下标(i,j)是指第i行第j列的神经元位置。网络B用到周期边界条件,即 , , , 。参数取 , , , 使得网络B中神经元是类型II兴奋性神经元。取 使得无噪声环境下每个神经元未耦合前都处于阈下受激发状态。D表示噪声强度,g2是网络B的内部耦合强度,g3是网络间层与层的耦合强度。
下面我们通过考察子网络A的时空斑图演化,来讨论在噪声环境下层间耦合强度对双层网络时空同步的影响。以下取N = 128,g1 = g2。
3. 环式子网络A的神经元放电行为和时空斑图
由环式网络A的构造可知,未耦合前网络A中单个神经元是周期1的神经元。当网络A与网络B耦合时,在噪声环境下神经元的放电行为会发生改变。下面以神经元1的放电行为为例来说明神经元放电行为的变化,且设 。
在无噪声环境中,当环式网络A未与格子网络B耦合,即g3 = 0时,神经元1是周期1放电,见图1(a);当两个网络耦合,耦合强度g3 = 2时,由于耦合神经元对网络的作用,网络A的神经元1呈现出周期2的放电行为,见图1(b);而在噪声环境中,当两个网络耦合时,受噪声和网络B神经元放电行为的影响,环式网络A的神经元1是混沌放电行为,见图1(c)。
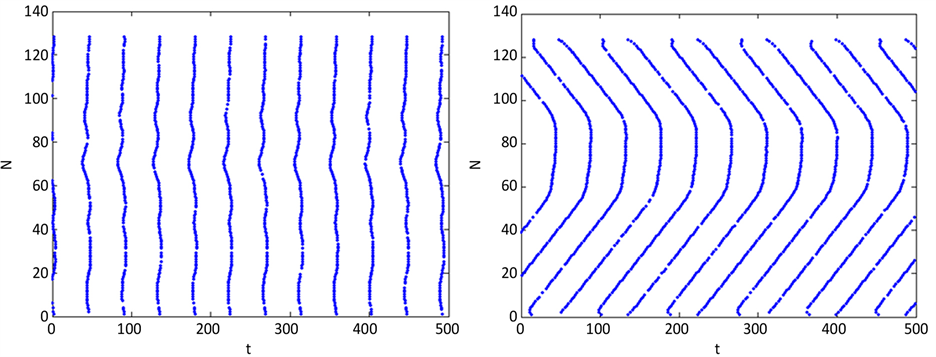
为了进一步看清环式网络A中神经元放电状况,我们画出其放电的时空斑图,见图2。由图2(a)可以看到,无噪声环境下,当网络A未与网络B耦合时,网络A是峰放电;当网络A与网络B强耦合时,放电脉冲随时间演化沿着某个空间方向传播,前部分神经元和后半部分神经元放电脉冲传播的方向相反,如图2(b)所示。这是因为两个最近邻的神经元以几乎固定的相位差放电,也就是神经元间相位锁定,相应地就导致神经元放电脉冲沿倾斜方向的行波传播。当有噪声刺激时,网络A神经元放电振幅受到扰动,产生小范围波动,见图2(c)和图2(d)。由图中可以看出噪声的引入并没有使网络A的时空斑图发生多大的改变。可见,两个网络的耦合会影响网络A的时空斑图的演化,而噪声对网络A的时空斑图的影响很小。
下面引入一个特征相关时间参数 来定量刻画神经元的时间有序行为。定义正则自相关函数如下
 (a) (b) (c)
(a) (b) (c)
Figure 1. Time series of the first neuron in ring-layer A: (a) D = 0, g3 = 0; (b) D = 0, g3 = 2; (c) D = 0.3, g3 = 0.5
图1. 网络A的神经元1的放电时序图:(a) D = 0,g3 = 0;(b) D = 0,g3 = 2;(c) D = 0.3,g3 = 0.5
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 2. Spatio-temporal firing patterns of subnetwork A in a raster plot: (a) D = 0, g3 = 0; (b) D = 0, g3 = 2; (c) D = 0.1, g3 = 0.08; (d) D = 0.1, g3 = 2
图2. 神经元网络A的时空斑图:(a) D = 0,g3 = 0;(b) D = 0,g3 = 2;(c) D = 0.1,g3 = 0.08;(d) D = 0.1,g3 = 2
这里 是第i个神经元在时间t的膜电位, 是时滞, 记为对时间t的平均。第i个神经元的特征相关时间由表达式 (见文献 [11] )来估计。对每个神经元有 个数据的极限和离散样本情况,可定义 ,这里 , 是样本时间, 是时间序列的长度。因此,特征相关时间参数可定义为 ,这里 是对所有神经元的平均。特征相关时间参数又称为有序参数,用来刻画神经元网络的时间有序程度。显然,神经元放电越有序,特征相关时间越长。
下面考察网络A里神经元放电的有序程度。图3给出无噪声环境和噪声环境(取噪声强度D = 0.1)下网络A的有序参数 随着网络间耦合强度g3变化而变化的趋势图。由图中可以看出两种情形下网络有序参数 的变化曲线都有一个凹槽,即曲线有低谷出现,这表明网络在某些特殊的耦合强度值出现最差的时空放电秩序。这是因为在两个网络的耦合过程中格子网络B一度占着主导地位,从而牵制环式网络A,使
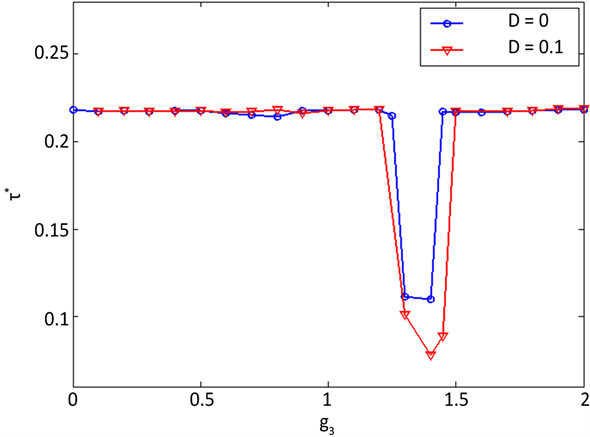
Figure 3. Variation of the order parameter with respect to the interlayer coupling strength g3 for D = 0 and D = 0.1, respectively
图3. 无噪声和噪声(D = 0.1)环境下有序参数 随网络间耦合强度g3的变化
其出现无序行为。两曲线均在g3 = 1.4时出现最小值,且在其它地方取值变化不大,这表明噪声的变化对神经元的放电活动影响很小,时空斑图对噪声具有鲁棒性。
4. 结论
本文研究噪声环境下的环–格子耦合神经元网络中环式子网络A的放电行为和时空斑图演化,发现神经元的放电行为和时空斑图的演化主要受两个网络耦合程度的影响。随着层间耦合强度增大,网络B会影响网络A神经元的放电有序性,在非噪声环境中网络间的耦合可以使环式网络中某些神经元的放电行为出现从周期1到周期2的转迁,而噪声会使耦合的周期1神经元出现混沌放电行为。对于格子网络B的动力学行为我们将在以后进一步研究。研究多层神经网络的动力学行为对理解和认识神经元系统的认知功能具有非常重要的理论意义。本文的结果对理解生物器官的功能及其运作机理具有一定的参考价值。
基金项目
国家自然科学基金(11672074),福建省教育厅JK项目(JK2015007)和福建省自然科学基金(2016J01003, 2018J01655)。
文章引用
郑艳红. 双层神经元网络中子网络的时空斑图研究
Spatio-Temporal Pattern in a Subnetwork of a Bi-Layer Neuronal Network[J]. 生物物理学, 2018, 06(03): 50-56. https://doi.org/10.12677/BIPHY.2018.63005
参考文献
- 1. Morris, C. and Lecar, H. (1981) Voltage Oscillations in the Bar-nacle Giant Muscle Fiber. Biophysical Journal, 35, 193-213. https://doi.org/10.1016/S0006-3495(81)84782-0
- 2. Pikovsky, A.S. and Kurths, J. (1997) Coherence Resonance in a Noise-Driven Excitable System. Physical Review Letters, 78, 775-778. https://doi.org/10.1103/PhysRevLett.78.775
- 3. 方小玲, 于洪洁. 复杂脑网络研究进展[J]. 力学进展, 2007, 37(4): 611-613.
- 4. Sun, X.J., Lei, J.Z., Kurths, J., Lv, S.J. and Lu, Q.S. (2011) Burst Synchronization Transition in a Neuronal Network of Subnetworks. Chaos, 21, Article ID: 016110. https://doi.org/10.1063/1.3559136
- 5. Lameu, E.L., Batista, C.A.S., Batista, A.M., Iarosz, K., Viana, R.L., Lopes, S.R. and Kurths, J. (2012) Suppression of Bursting Synchronization in Clustered Scale-Free (Rich-Club) Neuronal Networks. Chaos, 22, Article ID: 043149. https://doi.org/10.1063/1.4772998
- 6. Batista, C.A.S., Lameu, E.L., Batista, A.M., Lopes, S.R., Pereira, T., Za-mora-López, G., et al. (2012) Phase Synchronization of Bursting Neurons in Clustered Small-World Networks. Physical Review E, 86, Article ID: 016211. https://doi.org/10.1103/PhysRevE.86.016211
- 7. Zheng, Y.H. and Wang, H.X. (2015) Chaotic Burst Synchro-nization in a Two-Small-World-Layer Neuronal Network. International Journal of Modern Physics C, 26, Article ID: 1550051. https://doi.org/10.1142/S0129183115500515
- 8. Nicholls, J.G.., et al. 神经生物学——从神经元到脑[M]. 北京: 科学出版社, 2003.
- 9. Sun, X.J. and Lu, Q.S. (2009) Pattern Synchronization in a Two-Layer Neu-ronal Network. Chinese Physics Letters, 26, Article ID: 060507.
- 10. Yu, H.T, Wang, J., Liu, C., Deng, B. and Wei, X.L. (2011) Vibrational Resonance in Excitable Neuronal Systems. Chaos, 21, Article ID: 043101. https://doi.org/10.1063/1.3644390
- 11. Zhou, C.S., Zemanová, L., Zamora-López, G., et al. (2007) Struc-ture-Function Relationship in Complex Brain Networks Expressed by Hierarchical Synchronization. New Journal of Physics, 9, 178. https://doi.org/10.1088/1367-2630/9/6/178