三角形网格下对流扩散方程的无震荡格式 A Non-Oscillatory Scheme for Convection Diffusion Equations on Triangular Meshes

doi:10.12677/IJFD.2018.62004

International Journal of Fluid Dynamics
Vol.06 No.02(2018), Article ID:25406,10 pages
10.12677/IJFD.2018.62004

A Non-Oscillatory Scheme for Convection Diffusion Equations on Triangular Meshes

Juan Zhao, Wei Gao^*

●How to Cite this Article

School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia

Received: May 24^th, 2018; accepted: Jun. 6^th, 2018; published: Jun. 14^th, 2018

ABSTRACT

Construction of oscillation-free schemes on unstructured meshes plays a key role on numerical solutions to convection dominated problems. A new NVSF (Normalized Variable and Space Formulation) scheme is presented on triangular meshes. The typical test cases show that the present scheme can suppress unphysical oscillations and possess good accuracy.

Keywords:Convection Diffusion Equation, Triangular Meshes, Non-Oscillatory Scheme

三角形网格下对流扩散方程的无震荡格式

赵娟，高巍^*

内蒙古大学数学科学学院，内蒙古呼和浩特

收稿日期：2018年5月24日；录用日期：2018年6月6日；发布日期：2018年6月14日

摘要

当计算区域为不规则几何时，在非结构网格下构造一个无震荡的格式一直是对流扩散方程研究的重要内容。基于三角网格，本文构造一个新的NVSF (Normalized Variable and Space Formulation)格式。典型算例表明，此数值格式不仅可以有效抑制非物理震荡，而且具有良好的精度。

关键词 :对流扩散方程，三角形网格，无震荡格式

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

对流占优问题的计算在流体动力学中有着重要的意义。结构网格下，已有很多NVF (Normalized Variable Formulation) [1] 高分辨率格式，如SMART [2] ，CLAM [3] ，HOAB [4] ，CUBISTA [5] ，OSHER [6] ，这些高阶格式不仅具有很好的精度，而且满足对流有界性，并在间断解处不产生非物理震荡。

而当遇到的问题具有不规则几何时，结构网格的几何适应性很差。这样NVF高分辨率格式无法直接运用。因此将NVF格式推广到无结构网格下，对于数值计算十分重要。M. S. Darwish [7] 提出的非结构网格下NVSF (Normalized Variable and Space Formulation)格式是这方面的基础研究工作之一。在 [7] 中指出，在无结构网格下，如图1所示，计算界面f的值不仅与相邻的节点的值有关，也与这些节点所在的位置有关。

本文基于三角形网格下，在 [7] 的研究基础上，利用CBC (Convection Boundedness Criterion) [8] 对流有界性准则，构造一个新的NVSF格式,，此格式在间断处很好地抑制非物理震荡。本文的具体安排如下：第二节为非结构网格下格式的构造，第三节为三角网格下的变量关系，第四节为时间离散方法，第五节为具体的数值算例及结果讨论，第六节给出结论。

2. 非结构网格下格式的构造

2.1. 非一致网格下的NVSF的正则化

在结构网格下，数值格式在对对流项离散时，一般会用到该界面相邻的三个节点。而在非一致网格下界面f的值不仅与相邻的节点的值有关，也与这些节点所在的位置有关。在非一致网格下，我们选取的节点为界面f的相邻的三个节点。如图1所示，U，C，D分别为f的上游，中心和下游节点，分别位于 $x_{U}$ , $x_{C}$ , $x_{D}$ 处。这三个节点上的值为 $ϕ_{U}$ , $ϕ_{C}$ , $ϕ_{D}$ ，界面f的值为 $ϕ_{f}$ ，位于 $x_{f}$ 处。在非一致网格下， $ϕ_{f} = f (ϕ_{U}, ϕ_{C}, ϕ_{D}, x_{U}, x_{C}, x_{f}, x_{D})$ ，由正则化变量定义：

$\hat{ϕ} = \frac{ϕ - ϕ_{U}}{ϕ_{D} - ϕ_{U}}, \hat{x} = \frac{x - x_{U}}{x_{D} - x_{U}}$

得到 ${\hat{ϕ}}_{f} = f ({\hat{ϕ}}_{C}, {\hat{x}}_{C}, {\hat{x}}_{f})$ 图2,图3分别为正则化前后的变量关系。通过正则化后我们看到 ${\hat{ϕ}}_{f}$ 的值是依赖于 ${\hat{ϕ}}_{C}$ , ${\hat{x}}_{C}$ 和 ${\hat{x}}_{f}$ 的值。

2.2. 对流项有界性准则

M. S. Darwish指出由Gaskell和Lau [8] 提出的对流有界性准则CBC是适用于非结构网格的。这个准则在正则变化的基础上指出，对于一个具有有界性的格式，满足以下条件：

${\begin{array}{l} {\hat{ϕ}}_{C} < {\hat{ϕ}}_{f} = f ({\hat{ϕ}}_{C}) < 1, 0 < {\hat{ϕ}}_{C} < 1 \\ {\hat{ϕ}}_{f} = {\hat{ϕ}}_{C}, {\hat{ϕ}}_{C} \leq 0 \\ {\hat{ϕ}}_{f} = {\hat{ϕ}}_{C}, {\hat{ϕ}}_{C} \geq 1 \end{array}$ (1)

关于精度问题，Leonard [9] 提出在结构网格上利用NVF得出的格式是满足二阶或三阶精度。在[9]

Figure 1. Three neighboring mesh points and the mesh face on unstructured meshes

图1. 非一致网格下三个相邻的节点及单元边界

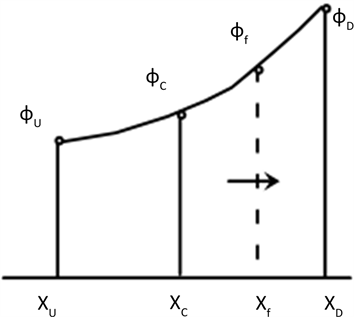
Figure 2. The relationship between variables before the regularization

图2. 正则化前的变量关系

Figure 3. The relationship between variables after the regularization

图3. 正则化后的变量关系

中，一个格式为二阶精度的充分必要条件是其表达式过点 $Q (0.5, 0.75)$ ；而对于非一致网格(NVSF)的情况，所构造的格式是二阶精度的充分必要条件是其表达式过点 $Q ({\hat{x}}_{C}, {\hat{x}}_{f})$ 。图4为几种格式在结构网格下与非一致网格下的正则变量图。

2.3. 新格式的构造

由上面可知构造一个有界性的新格式首先要满足CBC准则，即式(1)。并且为保证构造的新格式具有二阶精度，必须通过点 $({\hat{x}}_{C}, {\hat{x}}_{f})$ 。我们令

${\hat{φ}}_{f} = a {\hat{φ}}_{C}^{3} + b {\hat{φ}}_{C}^{2} + c {\hat{φ}}_{C} + d$ (2)

由上面可知此格式需满足：

Figure 4. Normalized Variable Diagram (NVD) for several linear schemes formulated using NVSF

图4. 利用NVSF构造的几种线性格式的正则变量图(NVD)

${\begin{cases} {\hat{φ}}_{f} (0) = 0 \\ {\hat{φ}}_{f} ({\hat{x}}_{c}) = {\hat{x}}_{f} \\ {\hat{φ}}_{f} (1) = 1 \end{cases}$ (3)

我们要构造的新格式与非一致网格下的Quick [7] 格式在处 $({\hat{x}}_{C}, {\hat{x}}_{f})$ 的导数相同，即

${\hat{φ}}^{'}_{f} ({\hat{x}}_{c}) = \frac{{\hat{x}}_{f} ({\hat{x}}_{f} - 1)}{{\hat{x}}_{c} ({\hat{x}}_{c} - 1)}$ (4)

将(3) (4)带入(2)式中解得

${\begin{cases} a = \frac{{({\hat{x}}_{c} - {\hat{x}}_{f})}^{2}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} \\ b = \frac{3 {\hat{x}}_{c}^{2} {\hat{x}}_{f} + {\hat{x}}_{c} {\hat{x}}_{f} - 2 {\hat{x}}_{c}^{3} - {\hat{x}}_{c} {\hat{x}}_{f}^{2} - {\hat{x}}_{f}^{2}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} \\ c = \frac{{\hat{x}}_{c}^{4} + {\hat{x}}_{c} {\hat{x}}_{f}^{2} + {\hat{x}}_{c} {\hat{x}}_{f} - 3 {\hat{x}}_{c}^{2} {\hat{x}}_{f}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} \\ d = 0 \end{cases}$

最后得到一个一致网格下的新格式，如图5新格式是满足CBC准则的。

$\begin{matrix} {\hat{φ}}_{f} = \frac{{({\hat{x}}_{c} - {\hat{x}}_{f})}^{2}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} {\hat{φ}}_{C}^{3} + \frac{3 {\hat{x}}_{c}^{2} {\hat{x}}_{f} + {\hat{x}}_{c} {\hat{x}}_{f} - 2 {\hat{x}}_{c}^{3} - {\hat{x}}_{c} {\hat{x}}_{f}^{2} - {\hat{x}}_{f}^{2}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} {\hat{φ}}_{C}^{2} \\ + \frac{{\hat{x}}_{c}^{4} + {\hat{x}}_{c} {\hat{x}}_{f}^{2} + {\hat{x}}_{c} {\hat{x}}_{f} - 3 {\hat{x}}_{c}^{2} {\hat{x}}_{f}}{{\hat{x}}_{c}^{2} {({\hat{x}}_{c} - 1)}^{2}} {\hat{φ}}_{C} \end{matrix}$

非一致网格在退化为结构网格时，点 $({\hat{x}}_{C}, {\hat{x}}_{f})$ 退化为点 $(0.5, 0.75)$ ，则得到结构网格下的新格式为

${\hat{ϕ}}_{f} = {\hat{ϕ}}_{C}^{3} - \frac{5}{2} {\hat{ϕ}}_{C}^{2} + \frac{5}{2} {\hat{ϕ}}_{C}$ (5)

3. 三角形剖分的变量关系

现将计算区域利用EasyMesh进行三角形剖分，而这种剖分得到的是非结构网格。在这种三角形网格下，变量的关系如图6所示。其中f为相邻两个三角形界面的中点，U为相邻两个三角形其中的一个顶点，C，D分别为这两个相邻三角形的重心。利用EasyMesh进行三角形剖分时，生成每个三角形的顶点坐标，同时每一个三角形的重心坐标也可以计算得到，各个点之间的距离也可以得到。将构造的非一致网格下的新格式应用到这种非结构网格下时，首先可利用单元三角形面积积分来求 $φ_{C}, φ_{D}$ 的值，还需知道上游 $φ_{U}$ 的值。现利用围绕顶点U的三角形重心处的值来估计 $φ_{U}$ 的值，记 $φ_{i}$ 为围绕U点各个三角形重心的值， $d_{i}$ 为U点到各个相邻三角形重心的距离，n为围绕U点的三角形个数，估计值式子如下：

Figure 5. New Format Curve and CBC Guidelines Area (area of dotted line)

图5. 新格式曲线与CBC准则区域(虚线区域)

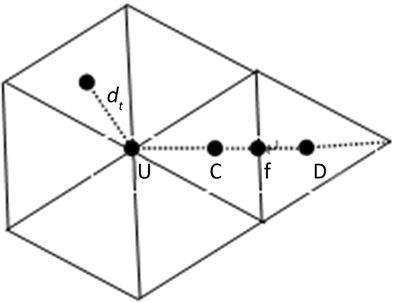
Figure 6. The relationship between variables of the triangle mesh

图6. 三角形网格下的变量关系

$φ_{U} = \frac{\sum_{i = 1}^{n} \frac{φ_{i}}{d_{i}}}{\sum_{i = 1}^{n} \frac{1}{d_{i}}}$

4. 时间的离散

完成了关于空间导数的离散后，得到了关于时间t的一个常微分方程，即 $\frac{d \bar{ϕ}}{d t} = L (ϕ)$ 。为了抑制非物理震荡，采用的是三阶TVD Runge-Kutta [10] 格式：

${\begin{array}{l} ϕ^{(1)} = ϕ^{n} + L (ϕ^{(1)}) \\ ϕ^{(2)} = \frac{3}{4} ϕ^{n} + \frac{1}{4} [ϕ^{(1)} + L (ϕ^{(1)})] \\ ϕ^{n + 1} = \frac{1}{3} ϕ^{n} + \frac{2}{3} [ϕ^{n} + L (ϕ^{n})] \end{array}$

5. 数值算例

5.1. 线性对流方程

一维线性对流方程

$\frac{\partial ϕ}{\partial t} + α \frac{\partial ϕ}{\partial x} = 0$ , $x \in [a, b]$ , $t > 0$ (6)

给定初值 $ϕ (x, 0) = ϕ_{0} (x)$ , $α = 1$ 。

5.1.1. 情形1

首先给定以下的初值 $ϕ (x, 0) = ϕ_{0} (x) = \sin (2 π x)$ ，在区间 $[0, 1]$ 上求解方程(6)， $C F L = 0.1$ ，利用结构网格下的新格式(5)、SMART [2] 格式、MUSCL [11] 格式计算方程数值解， $Δ x$ 分别取20、40、80、160、320。计算格式的 $L_{1}$ 误差、 $L_{2}$ 误差，同时算出数值精度阶(如表1)，计算公式如下：

$order = \frac{\ln E_{N} / E_{2 N}}{\ln 2}$

由表1可知，对于光滑解问题，结构网格下的新格式可以达到理论上二阶精度。

5.1.2. 情形2

对于上述的方程(6)，选取间断初值

$ϕ (x, 0) = {\begin{matrix} 1, \\ 0, \end{matrix} \begin{matrix} x \leq 0 \\ x \geq 0 \end{matrix}$

计算区间为 $[- 1, 1]$ ，等分为800等份，计算时间T为0.1，图7表明，结构网格下的新格式对间断解

的计算有很好的逼近效果。

5.2. 二维线性对流方程

下面将利用非结构网格下的新格式对二维对流方程进行求解，选取Doswell [12] 模型，

Table 1. Errors and orders for several selected schemes

表1. 格式误差与数值精度阶对比

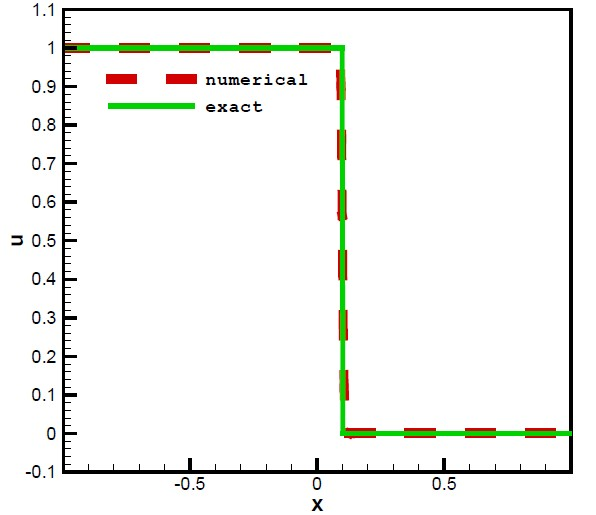
Figure 7. Comparison of numerical and exact results for the new condition

图7. 新格式的数值解与真实解

$\frac{\partial ϕ}{\partial t} + \frac{\partial (a ϕ)}{\partial x} + \frac{\partial (b ϕ)}{\partial y} = 0$

此数学模型在速度场中有稳定的切向速度

$ν_{t} (r) = \frac{1}{ν_{\max}} \frac{\tanh (r)}{\cosh^{2} (r)}$

在计算的过程中，令，并在该场中有

$a (x, y) = - \frac{y - x_{0}}{r} ν_{t} (r)$ , $b (x, y) = \frac{x - y_{0}}{r} ν_{t} (r)$

其中 $(x_{0}, y_{0})$ 为旋转中心， $r = \sqrt{{(x - x_{0})}^{2} + {(y - y_{0})}^{2}}$ 表示区域内任意一点到中心的距离，角速度定义为 $ω = \frac{ν_{t} (r)}{r}$ 。选取计算区域为 $[0, 8] \times [0, 8]$ ，利用EasyMesh对计算区域进行三角形网格剖分，图8为剖分图。在这种剖分下得到14,818个单元三角形，7570个顶点，22,384条边。此模型的精确解为

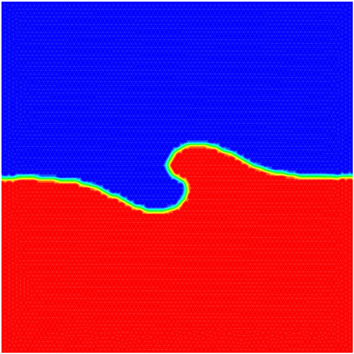
$ϕ (x, y, t) = \tanh [\frac{y - x_{0}}{δ} \cos (ω t) - \frac{x - y_{0}}{δ} \sin (ω t)]$

参数 $δ$ 表示的是锋面的梯度，取 $δ = 10^{- 6}$ ，得到的数值结果如图9。(a)显示了数值解的2D图，反应了锋面生成的漩涡形状，(b)显示了数值解的3D图像。

6. 结论

本文基于三角形网格和CBC准则构造一个新的NVSF格式，数值算例表明此格式可适用于非结构网格，并且在间断解处很好地抑制了非物理震荡。退化后的结构网格下的格式也有很好的精度。本文为无

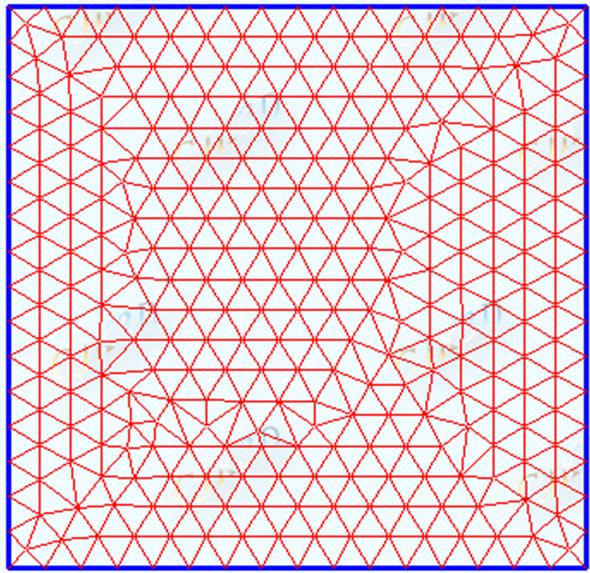
Figure 8. Triangulation diagram of EasyMesh

图8. EasyMesh的三角形剖分图

(a) (b)

Figure 9. Exact and numerical solutions of Doswell

图9. Doswell的数值解的2D、3D图像

结构网格下的问题提供了一个很好的解决方法。下一步的工作计划利用本文中的格式计算不同的对流扩散方程，比如二维浅水方程等。

基金项目

本文由内蒙古自然科学基金项目(2015MS0101)和内蒙古自治区人才开发基金项目(12000-1300020240)支持。

文章引用

赵娟,高巍. 三角形网格下对流扩散方程的无震荡格式
A Non-Oscillatory Scheme for Convection Diffusion Equations on Triangular Meshes[J]. 流体动力学, 2018, 06(02): 23-32. https://doi.org/10.12677/IJFD.2018.62004

参考文献

1. Gottlieb, S. and Shu, C.-W. (1998) Total Variational Diminishing Runge-Kutta Schemes. Mathematics of Computation, 67, 73-85. https://doi.org/10.1090/S0025-5718-98-00913-2

2. Van Leer, B. (1977) Towards the Ultimate Conservative Difference Scheme. V. A Second-Order Sequel to Godunov’s Method. Journal of Computational Physics, 23, 101-136.

3. Lenard, B.P. (1988) Simple High-Accuracy Resolution Program for Convective Modeling of Discontinuities. International Journal for Numerical Methods in Fluids, 8, 1291-1318. https://doi.org/10.1002/fld.1650081013

4. Doswell, C.A. (1998) A Kinematic Analysis of Frontogenesis Associated with a Non-Divergent Vortex. Journal of the Atmospheric Sciences, 41, 1242-1248. 2.0.CO;2>https://doi.org/10.1175/1520-0469(1984)041<1242:AKAOFA>2.0.CO;2

5. Gaskell, P.H. and Lau, A.K.C. (1988) Curvature-Compensated Convective Transport: SMART, A New Boundedness-Preserving Transport Algorithm. Interna-tional Journal for Numerical Methods in Fluids, 8, 617-641. https://doi.org/10.1002/fld.1650080602

6. Van Leer, B. (1974) Towards the Ultimate Conservative Difference Scheme: II. Monotonicity and Conservation Combined in a Second-Order Scheme. Journal of Computation Physics, 14, 361-370. https://doi.org/10.1016/0021-9991(74)90019-9

7. Wei, J.J., Yu, B., Tao, W.Q., Kawaguchi, Y. and Wang, H.S. (2003) A New High-Order-Accurate and Bounded Scheme for Incompressible Flow. Numerical Heat Transfer, Part B: Fundamentals, 43, 19-41. https://doi.org/10.1080/713836153

8. Alves, M.A., Oliveire, P.J. and Pinho, F.T. (2003) A Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection. International Journal for Numerical Methods in Fluids, 41, 47-75. https://doi.org/10.1002/fld.428

9. Chakravarthy, S.R. and Osher, S. (1983) High Resolution Applications of the OSHER Upwind Scheme for the Euler Equations. AIAA Paper 83-1943. https://doi.org/10.2514/6.1983-1943

10. Darwish, M.S. and Moukallod, F.H. (1994) Normalized Variable and Space Formulation Methodology for High-Resolution Schemes. Numerical Heat Transfer, Part B, 26, 79-96. https://doi.org/10.1080/10407799408914918

11. Spalding, D.B. (1972) A Novel Finite Dif-ference Formulation for Differential Expressions Involving Both First and Second Derivatives. International Journal for Nu-merical Methods in Engineering, 4, 551-559. https://doi.org/10.1002/nme.1620040409

12. Leonard, B.P. (1987) SHARP Simulation of Discontinuities in Highly Con-vective Steady Flow. NASA Technical Memorandum 100240, ICOMP-87-9.

期刊菜单