International Journal of Fluid Dynamics
Vol.
07
No.
03
(
2019
), Article ID:
32327
,
10
pages
10.12677/IJFD.2019.73010
Numerical Simulation of Flood Confluence Flow Field Based on Finite Volume Method
Bo Yu, Xiyuan Li
School of Mathematics and Statistics, Wuhan University, Wuhan Hubei
Email: boy_kyzy@163.com
Received: Sep. 2nd, 2019; accepted: Sep. 18th, 2019; published: Sep. 25th, 2019

ABSTRACT
In this study, the finite volume method was used to simulate and analyze the complex flow field distribution of flood discharge and flood discharge project, and the confluence flow field near the flood gate was analyzed. After the flow field changes, the flow field distribution characteristics and flow velocity parameters are proposed. The influence of confluent flow field on the flood storage project buildings and nearby levees is analyzed. The hydraulic indexes near the flood control area and the flood diversion area are proposed, which are the flood gate layout and dam. Protection provides a scientific basis.
Keywords:Finite Volume Method, Shallow Water Wave Equation, Numerical Calculation, Merging Flow
基于有限体积法对洪水汇合流流场的数值模拟
于博,李喜园
武汉大学数学与统计学院, 湖北 武汉
Email: boy_kyzy@163.com
收稿日期:2019年9月2日;录用日期:2019年9月18日;发布日期:2019年9月25日
摘 要
本研究采用有限体积法,通过数值计算,模拟分析了行洪、蓄洪工程退洪、和分流洪水汇合的复杂流场分布,分析了洪闸附近的汇合流场结构,对比洪闸工程修建前、后的流场变化,提出流场分布特征和流速参数,重点分析汇合流场对蓄洪工程建筑物和附近大堤的影响,提出退洪区、分洪区附近的水力学指标,为洪闸布置、堤坝防护提供科学依据。
关键词 :有限体积法,浅水波方程,数值计算,汇合流
Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
天然河道中的水流多属缓流,流量也比较均匀。在发生洪水时,行洪的流量以及流速增大且分布不均匀。尤其在河道中修建了洪闸等蓄洪工程建筑物后,加大了上下游洪水的势能落差,在通过洪闸后洪水的比能也相较于下游河道中水流大得多,这样巨大的能量,若不采取消能措施,会对下游河床以及堤坝具有更强的冲击力,这样反复的作用使得坝口及分叉河道汇流处流场十分复杂。
多股洪水汇合流问题最终简化为求解控制水流运动的非恒定流的拟线性双曲型偏微分方程组。在洪水传播过程中,垂直尺度变化较小,对Navier-Stokes方程沿垂直水深作积分平均,即可得到洪水汇合流的二维浅水波模型,也称为圣维南方程组。
对于浅水波的研究,主要有有限差分法 [1] 、有限元法 [2] [3] [4] 、有限体积法 [5] [6] [7] [8] 、混合分析法 [9] 。空气动力学高精度高分辨率格式也被引入到计算水动力学的研究中,例如Godunov型有限体积格式 [10] ,高分辨率的ENO格式 [11] 。本文借助格林公式对地形源项进行处理,建立了一种和谐的WAF型有限体积格式,模拟了洪水传播过程中带激波和干湿边界的浅水波方程,以几个工况为例进行模拟,对比实际数据,研究了洪水波演进、汇合流复杂流场分布以及不规则河床地形河道形状对洪水波计算的影响。
2. 数学模型
2.1. 控制方程
通过建立蓄洪区退洪、长江河道行洪和分洪区分洪的数学物理方程,采用二维浅水波方程组研究多股洪水汇合流问题。浅水波方程组采用以水位和单宽流量为变量的守恒形式,即:
(1)
式中t代表时间,x和y分别表示空间变量。U表示物理守恒变量, 、 分别为x和y方向的通量,S表示源项:
其中
,
表示x,y方向的单宽流量,u,v分别表示x,y两个方向上的流速,
为自由流表面高程,h为水深,
为河道地形函数。源项S由两部分构成: 则表示地形底坡;
表示摩阻底坡,根据经验公式给出:
,
。其中,
为谢才系数,
为曼宁系数。为简化模型,本文不考虑与地球自转相关的科氏力。
则表示地形底坡;
表示摩阻底坡,根据经验公式给出:
,
。其中,
为谢才系数,
为曼宁系数。为简化模型,本文不考虑与地球自转相关的科氏力。
2.2. 计算方法
本研究采用三角形网格处理计算区域,计算方法采用有限体积法模拟区域水位、水流、流量和流态。考虑到问题物理区域的复杂性,采用三角网格离散计算区域,三角形网格和物理量布置如图1a所示。数值计算方法采用目前比较成熟的方法,可满足计算精度和稳定性要求。计算方法构造如下:
引入算子 将浅水波方程改写成向量形式:
(2)
其中 ,对上式在控制区域上积分得:
利用格林公式得:
其中, 为单元边界的单位外法向量。半离散有限体积法:
(3)
模拟的是守恒量的单元积分平均值:
其中 为计算单元 的面积, 为源项为单元平均。这样,问题等价于给出单
元法向通量和源项的近似,进而求解一个关于时间的常微分方程。根据二维浅水波方程组法向通量的旋转不变性,可以将转化成一个一维的Riemann问题近似解 [12] (图1b):
 (a)
(a)
 (b)
(b)
Figure 1. The structure of approximate solution of Riemann problem
图1. Riemann问题近似解的结构
旋转矩阵 定义为:
(4)
其中, 为U旋转后的量,通量函数 满足 。进一步,采用时间向前差分离散得:
(5)
上式中源项采用中心差分进行离散,基于局部Riemann问题自相似解波系结构分析,采用TVD-WAF格式给出数值通量为:
(6)
其中 为第k个波处的数值通量的跳量, 为波 的Courant数:
 (7)
(7)
通量限制器 ,其中变量 为:
(8)
上式中变量p为
, ,
。式(7)中波系间的数值通量可以有HLLC近似里面求解器给出:
,
。式(7)中波系间的数值通量可以有HLLC近似里面求解器给出:
(9)
下标 表示通量向量的第k个分量,其中HLL求解器定义为:
(10)
其中,左右波速度 和 分别为 [13] :
(11)
其中 , 。接触间断波波速 的估计:
(12)
数值计算需要处理动边界问题,及计算单位处理干湿单元的问题。当计算单元边界为干湿边界时,左干河床 , ;右干河床: , 。 会自动和估计的干河床重合。
为了保证数值格式的稳定性,需要在进行计算时调整时间,采用:
(13)
其中 是Courant数。
为保证数值算法的结构的和谐性,首先用Green公式转化地形源项 ,然后利用中矩形公式进行离散。因此, 第二、三个分量为:
可以证明该格式是和谐的 [14] 。
2.3. 计算条件
1) 计算区域:计算模型要求计算研究区域上下游需要由足够的计算长度,避免进出口条件设置的影响。结合现有河道地形资料,选取洪闸上游约4 km、下游约10 km,共计约14 km为计算区域。河道地形采用工程区附近2011年地形资料。
2) 网格剖分:考虑计算区域边界不规则形,边界条件复杂性,计算方法采用三角形剖分算法将物理区域划分为规则性三角形组成的计算区域,计算网格数为37,082个,为兼顾整个计算区域,同时为提高计算精度,在洪闸、分洪区、蓄洪区出口附近,采用了网格加密处理(如图2)。
 (a)
(a) (b)
(b)
Figure 2. Computational area mesh Generation and Local encryption Generation Diagram
图2. 计算区域网格剖分与局部加密剖分图
2.4. 模型率定
模型利用洪闸附近水位~流量关系对计算河道的糙率进行了率定(表1)。通过分析糙率取值范围在0.023~0027。本研究采用河床糙率取值0.025。
Table 1. Model rate table
表1. 模型率定表

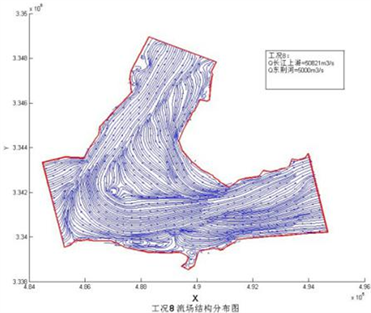


Figure 3. Distribution of flow field
图3. 流场分布
3. 数值计算
3.1. 长江与分洪汇合流计算
根据不同的计算需要设置了工况1~11。为了解蓄滞洪区工程建设前洪闸附近长江河道流场分布,考虑分洪任务要求,设置了计算工况8~11。通过该工况计算一方面掌握工程修建前,长江与分洪汇合流场分布。分流洪水在入江口处受长江主流顶托,流场向左岸偏离,混合长江洪水后进入下游河道,未直接影响长江上游河道(图3)。分洪流量大小对汇合流场结构影响不大,在较大洪水情况下,工况8和工况10流场相似,在较小洪水情况下,工况9和工况11流场分布相似。
3.2. 洪闸、长江和分流汇合洪水计算
在以上计算基础上,为研究蓄洪区退洪,长江行洪和分流复杂汇合流问题,加入东荆河分流洪水影响,设置了工况1~7。通过计算观测,三股洪水形成混合流如图4,首先上游长江洪水退洪洪水接触混合,偏向主槽,然后于内荆河排水混合,上游混合流在河道内进行调整。在东荆河入江口处,长江洪水与东荆河分流洪水汇合,最后向右转弯,进入下游河道。长江洪水量越大,对下游挤压作用越大,长江洪水大时,东荆河洪水偏向左侧较明显,洪水相对小,向左偏向减弱;蓄洪区泄洪流量越大,对上游长江洪水阻挡作用越强,洪闸左侧回流淘刷强度越大。各工况不同位置监测点流速如表2。


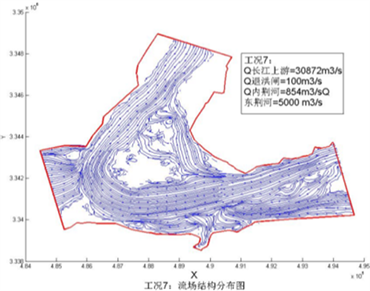

Figure 4. Distribution of flow field
图4. 流场分布
Table 2. Characteristic value of flow velocity at monitoring points of embankment
表2. 堤坝部分监测点流速特征值
4. 成果分析结论
1) 三股洪水同时汇合时,工程区域流场复杂,上游长江洪水同补元闸退洪洪水接触混合,受挤压偏向主槽,然后与内荆河排水混合,上游混合流在河道内进行短距离调整。在东荆河入口处,长江洪水再与东荆河分流洪水汇合,最后向右转弯,进入下游河道。
2) 通过流场分析,蓄洪区退洪过程一定程度上影响工程区长江洪水流场分布。通过不同工况数值计算,各监测点计算流速如图5。各工况测点流速大部分为0.05~0.3 m/s之间,在洪水相对较小时,堤防沿程各测点流速变化不大,长江洪水大于45,900 m3/s的工况时,在洪闸左侧长江下游堤段范围流速增加,最大值为0.31 m/s,结合流场分析,主要由于该区域为内荆河入江口处,同时叠加河道回流影响。

Figure 5. Flow velocity distribution of embankment toe in lower reaches of Yangtze River
图5. 长江下游堤脚流速分布
4. 结论
1) 蓄洪区退洪、长江行洪、东荆河分洪三股洪水汇合处流场结构非常复杂,在洪闸左侧长江下游河道出现两处较大范围的回流现象,但整体回流过程比较平稳,未出现主流偏离或主流折冲现象,整体布置比较安全。
2) 东荆河分流洪水同长江上游洪水汇合,主流偏左岸,然后流向下游,未直接影响长江上游区域,对补元闸工程、长江上游堤防影响不大。
3) 蓄洪区退洪与长江汇合流场复杂,工程附近流速较小,闸左、右两侧流速v < 0.4 m/s。蓄洪区退洪对工程附近长江下游流态有一定影响,增强了闸后长江下游堤防附近的回流强度。
文章引用
于 博,李喜园. 基于有限体积法对洪水汇合流流场的数值模拟
Numerical Simulation of Flood Confluence Flow Field Based on Finite Volume Method[J]. 流体动力学, 2019, 07(03): 83-92. https://doi.org/10.12677/IJFD.2019.73010
参考文献
- 1. Garcia, R. and Kahawita, R.A. (1989) Numerical Solution of the St. Venant Equations with MacCormack Finite Difference Scheme. International Journal for Numerical Methods in Fluids, 6, 507-527.
- 2. Akanbi, A.A. and Katopodes, N.D. (1988) Model for Flood Propagation on Initially Dry Land. Journal of Hydraulic Engineering, 114, 689-706. https://doi.org/10.1061/(ASCE)0733-9429(1988)114:7(689)
- 3. Cockburn, B. and Shu, C.W. (1989) TVB Runge-Kutta Local Projection Discontinuous Galerkin Finite Element Method for Scalar Conversation Laws II: General Framework. Mathematics of Computation, 52, 411-435. https://doi.org/10.2307/2008474
- 4. Cockburn, B., Lin, S.Y. and Shu, C.W. (1989) TVB Runge-Kutta Local Projection Dis-continuous Galerkin Finite Element Method for Scalar Conversation Laws III: One Dimensional Systems. Journal of Computational Physics, 84, 90-113. https://doi.org/10.1016/0021-9991(89)90183-6
- 5. Chen, G. and Noelle, S. (2017) A New Hydrostatic Reconstruction Scheme Based on Subcell Reconstructions. SIAM Journal on Numerical Analysis, 55, 758-784. https://doi.org/10.1137/15M1053074
- 6. Noelle, S., Pankratz, N., Puppo, G., et al. (2006) Well-Balanced Finite Volume Schemes of Arbitrary Order of Accuracy for Shallow Water Flows. Journal of Computational Physics, 213, 474-499. https://doi.org/10.1016/j.jcp.2005.08.019
- 7. 胡四一, 谭维炎. 用TVD格式预测溃坝洪水波的演进[J]. 水利学报, 1989(7): 1-11.
- 8. Bollermann, A., Chen, G., Kurganov, A., et al. (2013) A Well-Balanced Reconstruction of Wet/Dry Fronts for the Shallow Water Equations. Journal of Scientific Computing, 56, 267-290. https://doi.org/10.1007/s10915-012-9677-5
- 9. 梁爱国, 槐文信, 赵明登. 用混合有限分析法求解二维溃坝洪水波的演进[J]. 水利水电技术, 2005, 36(10): 34-37.
- 10. Alcrudo, F. and Garcia, N.P. (1993) A High-Resolution Godunov-Type Scheme in Finite Volumes for the 2D Shallow Water Equation. International Journal for Numerical Methods in Fluids, 16, 489-505. https://doi.org/10.1002/fld.1650160604
- 11. Harten, A., Engquist, B., Osherand, S., et al. (1987) A Uniformly High Order Ac-curacy Essentially Non-Oscillatory Schemes III. Journal of Computational and Applied Mathematics, 71, 231-303. https://doi.org/10.1016/0021-9991(87)90031-3
- 12. 杨金波, 李订芳, 陈华. 和谐WAF格式在带干河床浅水波方程中的应用[J]. 华中科技大学学报(自然科学版), 2012, 40(2): 54-57+61.
- 13. Toro, E.F. (1992) Riemann Problems and the WAF Method for Solving the Two-Dimensional Shallow Water Equations. Philosophical Transactions of the Royal Society of London. Series A, 338, 43-38. https://doi.org/10.1098/rsta.1992.0002
- 14. 杨金波. WAF和MUSCL-HLLC有限体积格式及其在溃坝问题中的应用[D]: [博士学位论文]. 武汉: 武汉大学, 2011: 45-59.
