Open Journal of Acoustics and Vibration
Vol.06 No.02(2018), Article ID:25162,7
pages
10.12677/OJAV.2018.62004
Global Bifurcation and Chaos of Liquid Sloshing in Liquid-Filled System
Junling Cao1,2, Shun Zhong1
1Department of Mechanics, Tianjin University, Tianjin
2Tianjin Lianda Comunication Development Co., LTD., Tianjin

Received: May 9th, 2018; accepted: May 22nd, 2018; published: May 29th, 2018

ABSTRACT
The nonlinear governing equations of the liquid sloshing modals in cylindrical storage tank are established. Through integration, the analytical expressions of the homoclinic orbits of this kind of system are got. Using the Melnikov method, the global dynamical behaviors are analyzed. The threshold of the chaotic motion is calculated, which shows that there exists global bifurcation and chaos when the system is subjected to greater disturbance. Meanwhile, numerical simulations are also given, which confirm the analytical results.
Keywords:Liquid-Filled System, Homoclinic Orbits, Chaotic Threshold
充液系统中液体晃动的全局分岔和混沌
曹俊灵1,2,钟顺2
1天津大学力学系,天津
2天津市联大通讯发展有限公司,天津

收稿日期:2018年5月9日;录用日期:2018年5月22日;发布日期:2018年5月29日

摘 要
本文以在各类工程中广泛应用的充液系统为研究对象,建立了柱形储液箱中液体晃动模态的非线性动力学方程组。通过积分,得到了该类系统的同宿轨道的解析表达式,并利用Melnikov方法对此系统的全局动力学行为进行分析,计算出系统在扰动条件下进入混沌的阈值,表明此类系统在受到较大扰动时,将发生全局分岔和混沌现象。同时,文中给出的算例证明了理论分析结果的正确性。
关键词 :充液系统,同宿轨道,混沌阈值

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
充液系统的非线性晃动动力学作为动力学与控制学科及其交叉学科的重要研究领域之一,广泛应用于工业、土木工程、汽车工程、船舶动力学、以及航空航天工业中 [1] [2] [3] 。以航空航天工程为例,液体晃动及其最优控制始终是航空航天飞行器总体设计的核心问题之一,迄今为止国内外航天力学工作者对充液系统的耦合晃动问题进行了广泛的研究 [4] [5] [6] [7] 。由于液体晃动问题可造成灾难性的破坏事故,使得液体晃动动力学的深入研究更加必要,同时,由于此问题存在大量的非线性因素,也使得此问题的理论研究更加复杂。
为建立有效的数学模型以研究充液系统的晃动动力学行为,尹立中 [8] ,马兴瑞等 [9] 将液体的速度势函数在自由液面处展开,利用Lagrange函数,导出了广义模态坐标下的非线性方程组,对系统的局部动力学行为进行理论分析。随着动力学理论的发展,全局动力学和混沌理论被广泛的应用于各种工程系统中 [10] [11] 。因此,将混沌行为的研究应用于充液系统是有必要和有意义的。
本文利用Melnikov方法对液体晃动方程的全局动力学行为 [12] 进行分析。Melnikov方法在解析分析非线性系统的混沌运动方面有着广泛的应用,主要分为单一扰动的情形 [13] ,或同频多扰动 [14] [15] 的情况。本文主要就单一扰动的情况进行分析,同频或非同频多扰动情况应用本文方法同样可以进行类似的分析。
2. 模型的建立
系统模型如图1所示,圆柱形储液箱半径为a,内部液体深度为h,定义OXYZ为绝对坐标系,局部坐标系 为柱坐标系。设液体燃料无旋,且与储液箱体接触角不变,根据速度势理论可得到液体晃动方程 [8] [9]
(1)
其中, 为无旋流体的速度势函数, 为储液箱平动速度矢量, 为储液箱转动角速度, 为转动半径, 为势函数, 为黏滞系数, 为液体密度, 为液面平均主曲率采用接触角不变假设时的常数,t为时间, 为散度算子。
不考虑储液箱体的转动,对液体的速度势函数进行模态展开 [9] ,其模态示意图如图2所示,得到描述液体晃动规律的方程组
(2)
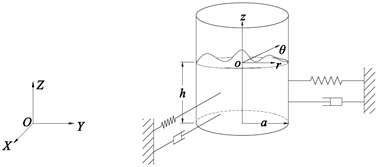
Figure 1. System model
图1. 系统模型

Figure 2. Modal of sloshing liquid
图2. 液体晃动模态示意图
其中, ( )为各阶广义模态位移, ( )为各阶模态阻尼, ( )为各阶模态频率, 、 、 、 ,( )为模态耦合系数。 和 分别为X和Y方向上的扰动,上标一点为相应变量的一阶导数,二点为二阶导数。
设系统的扰动形式为 , ,取液体晃动方程组中的第一阶主模态作为简化,得到
(3)
其中, 为液体晃动的第一阶主模态, 为一阶模态频率, 为X方向扰动的振幅, 为X方向扰动的频率, , , 和 为简化后的方程系数。
3. 全局分岔
为了便于讨论,将(3)改写为
(4)
其中, , , , , , , 。研究表明,在部分充液条件下,当充液深度相对较小时,上述各参数均为大于零的量 [16] 。
在方程(4)中 为一小量,其对应的无扰动力系统为
(5)
其对时间的一次积分为
(6)
对于不同的H值,它代表相平面上不同的轨道。
系统(5)有3个不动点,它们分别为: , 和 ,不难判定O、A点是中心,B点是鞍点 [17] 。
现在来讨论无扰动动力系统的同宿运动,当 ,由(6)式,得到
(7)
积分即得同宿轨道为:
(8)
或
(9)
其中 和 为积分常量。
当 时,得绕O、A两点的两族闭轨道,代表在稳定平衡位置附近的振动,当H增大时,振动的周期增大,当 时,代表另一类型的周期性振动。
对动力系统(4),定义Melnikov函数为:
(10)
其中, 。
故
(11)
式(11)中的第一个积分为
(12)
考虑式(11)中的第二个积分
(13)
其中,
(14)
(15)
将(12)和(13)代入式(11)中,得到Melnikov函数
(16)
Melnikov函数如果有限,则稳定流形和不稳定流形相交,Poincare映射有马蹄,从而存在着奇怪的不变集合,对我们研究的耗散系统,就有可能出现混沌,由 得到
(17)
为使方程(17)有根,必须有 ,故此,发生混沌的临界条件为
(18)
4. 算例
对非线性动力方程(4)进行数值计算,取
, ,
,
,
,得到关于扰动幅值g的分岔图(图3)和
时,系统的时程曲线,相图和Poincare截面,如图4所示,表明系统在给定参数条件下,扰动幅值增加,系统将发生同宿分岔并进入混沌。
,
,
,
,得到关于扰动幅值g的分岔图(图3)和
时,系统的时程曲线,相图和Poincare截面,如图4所示,表明系统在给定参数条件下,扰动幅值增加,系统将发生同宿分岔并进入混沌。
5. 结论
本文通过对液体晃动模态方程进行解析求解,得到了系统的同宿轨道的解析表达式,并利用Melnikov函数,确定了系统在受扰情况下发生混沌运动的阈值,表明系统在受到一定程度的扰动后,会发生同宿分岔和混沌运动。通过本文的结果,可以看到,全局动力学行为在液体晃动动力学分析中的重要性,局部分析结果往往只能对液体小幅晃动的情况进行预测和控制,当充液系统工作在较恶劣工况下,液体非小幅晃动时,系统的动力学行为更值得关注,本文的研究结果表明,当扰动较大时,系统发生混沌运动
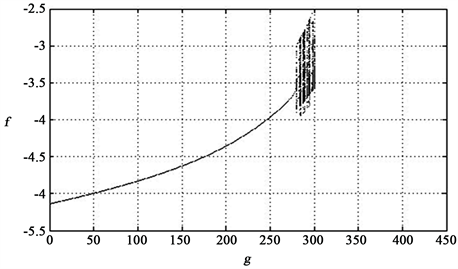
Figure 3. Bifurcation diagram
图3. 分岔图

 (a) (b)
(a) (b) (c)
(c)
Figure 4. Curves of the responses at g = 280 (a) Time history; (b) Phase plane; (c) Poincare mapping
图4. g = 280时的各种曲线 (a) 时程曲线;(b) 相图;(c) Poincare 映射
的机理是同宿分岔,液体晃动虽非小幅,但为有限幅,在工程应用中,这一情况更容易得到控制,而不会对系统造成破坏性的影响,因此,此结果可为工程优化设计和控制提供理论依据。
基金项目
国家自然科学基金青年项目(批准号:11502161)、天津市自然科学基金青年项目(合同号:13JCQNJC04300)。
文章引用
曹俊灵,钟 顺. 充液系统中液体晃动的全局分岔和混沌
Global Bifurcation and Chaos of Liquid Sloshing in Liquid-Filled System[J]. 声学与振动, 2018, 06(02): 29-35. https://doi.org/10.12677/OJAV.2018.62004
参考文献
- 1. Abramson, H.N. (2003) Dynamics of Contained Liquids: A Personal Odyssey. Applied Mechanics Review, 56, 1-7. https://doi.org/10.1115/1.1511517
- 2. Ibrahim, R.A. and Pilipchuk, V.N. (2001) Recent Advances in Liquid Sloshing Dynamics. Applied Mechanics Review, 54, 133-199. https://doi.org/10.1115/1.3097293
- 3. Pan, X. and Jin, W. (2005) Effect of Axial Vibration on Free Surface Flows in Cylindrical Liquid. Chinese Physics B, 14, 422-426. https://doi.org/10.1088/1009-1963/14/2/035
- 4. 王照林, 刘延柱. 充液系统动力学[M]. 北京: 科学出版社, 2002: 83-98.
- 5. Zhou, L., Chen, Y. and Chen, F. (2009) Stability and Chaos of a Damped Satellite Partially Filled with Liquid. Acta Astronautica, 65, 1628-1638. https://doi.org/10.1016/j.actaastro.2009.04.009
- 6. Askari, E. and Daneshmand, F. (2009) Coupled Vibration of a Partially Fluid-Filled Cylindrical Container with a Cylindrical Internal Body. Journal of Fluids and Structures, 25, 389-405. https://doi.org/10.1016/j.jfluidstructs.2008.07.003
- 7. Liu, Y., Zhu, J. and Luo, X. (2009) Bifurcation and Stabil-ity of an Improved Time-Delayed Fluid Flow Model in Internet Congestion Control. Chinese Physics B, 18, 3772-3776. https://doi.org/10.1088/1674-1056/18/9/026
- 8. 尹立中, 马兴瑞, 王本利, 邹经湘. 圆柱贮箱类液固耦合系统转动响应分析[J]. 振动工程学报, 2001, 14(1): 68-71.
- 9. 马兴瑞, 王本利, 苟兴宇. 航天器动力学-若干问题进展及应用[M]. 北京: 科学出版社, 2001: 329-335.
- 10. Shi, P., Han, D. and Liu, B. (2010) Chaos and Chaotic Con-trol in a Relative Rotation Nonlinear Dynamical System under Parametric Excitation. Chinese Physics B, 19, Article ID: 090306.
- 11. Lv, L., Li, G., Guo, L., Meng, L., Zou, J. and Yang, M. (2010) Generalized Chaos Synchronization of a Weighted Complex Network with Different Nodes. Chinese Physics B, 19, Article ID: 080507.
- 12. Kovaleva, A. (2010) The Melnikov Criterion of Instability for Random Rocking Dynamics of a Rigid Block with an Attached Secondary Structure. Nonlinear Analysis: Real World Applications, 11, 472-479. https://doi.org/10.1016/j.nonrwa.2008.12.001
- 13. Rasoul, A. and Hamid, R.Z.Z. (2010) Bifurcations of Limit Cy-cles for a Quintic Hamiltonian System with a Double Cuspidal Loop. Computers & Mathematics with Applications, 59, 1409-1418. https://doi.org/10.1016/j.camwa.2009.12.024
- 14. Zhou, L., Chen, Y. and Chen, F. (2010) Global Bifurcation Analysis and Chaos of an Arch Structure with Parametricand Forced Excitation. Mechanics Research Communications, 37, 67-71. https://doi.org/10.1016/j.mechrescom.2009.08.007
- 15. Zhang, W., Zhang, J.H., Yao, M.H. and Yao, Z.G. (2010) Multi-Pulse Chaotic Dynamics of Non-Autonomous Nonlinear System for a Laminated Composite Piezoelectric Rectan-gular Plate. Acta Mechanica, 211, 23-47. https://doi.org/10.1007/s00707-009-0210-3
- 16. Zhong, S. and Chen, Y. (2011) Bifurcation of Elastic Tank-Liquid Coupled Sloshing System. Applied Mathematics and Mechanics, 32, 1169-1176. https://doi.org/10.1007/s10483-011-1490-x
- 17. Chen, Y., Audrew, Y. and Leung, T. (1998) Bifurcation and Chaos in Engineering. Springe-Vereag, London, 66-76. https://doi.org/10.1007/978-1-4471-1575-5