Creative Education Studies
Vol.
08
No.
02
(
2020
), Article ID:
34901
,
5
pages
10.12677/CES.2020.82017
A Brief Discussion on Applications of Advanced Algebra in Modern Algebra Teaching
Qiufan Chen
College of Arts and Sciences, Shanghai Maritime University, Shanghai

Received: Mar. 12th, 2020; accepted: Mar. 27th, 2020; published: Apr. 3rd, 2020

ABSTRACT
In this paper, associated with actual experience in the teaching of modern algebra, several concrete examples are given to demonstrate how to apply advanced algebra in modern algebra, such as group, ring and field. Using the advanced algebra can not only change abstraction to concrete, but also flexibly develop the ways to solve problems, which would be useful for students to get an in-depth understanding of modern algebra.
Keywords:Modern Algebra, Advanced Algebra, Group, Ring, Field

浅谈高等代数在近世代数教学中的应用
陈秋帆
上海海事大学文理学院,上海

收稿日期:2020年3月12日;录用日期:2020年3月27日;发布日期:2020年4月3日

摘 要
本文结合近世代数的教学实践经验,通过具体的例子介绍了高等代数在群、环和域等近世代数问题中的应用。应用高等代数,不但能化抽象为具体,而且能开拓解题思路,对学生深入理解近世代数有积极作用。
关键词 :近世代数,高等代数,群,环,域

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近世代数是本科数学系的专业基础课,它是现代数学的重要基础,主要研究群、环、域等代数结构。近世代数着重培养学生的抽象思维方式,即如何从具体的数学研究对象中提炼出它们的本质(群、环、域的定义),并且从这些本质的共性中推导出其它共性,如何对研究对象进行分类,以及学会不同研究对象之间的比较方式等 [1] [2] [3] [4]。这些思考方式的训练不仅对整个数学领域是重要的,对于其他学科也是基本的,而且随着数字计算与通信的发展,近世代数已成为通信与计算机科学的重要工具 [5] [6] [7]。近世代数作为一门基础课程,一方面课时少并且没有后续课程,不少学生只是听到一些莫名其妙的定义和定理,做一点形式逻辑的推导,没有领会到这门课程的真谛;另一方面,该课程概念众多,理论知识多以证明为主,主要是符号的运算,具有高度的抽象性。因此,学生学习和掌握的效果并不让人十分满意。近年来,如何提高近世代数的教学效果成为了教育工作者的研究内容 [8] [9]。然而笔者在教学中发现,将近世代数与高等代数 [10] [11] 的知识联系起来进行教学的效果还不错,例如向量空间与交换群,向量空间的同态与群同态,向量子空间的直和与群的直和,不可约多项式与不可约元等。这种类比与呼应,有利于学生对抽象理论的理解,使学生认为近世代数是有用、有趣且不是那么困难的。本文结合实例介绍高等代数在近世代数教学中的应用,希望能起到抛砖引玉之用。
2. 在群论中的应用
群的公理化定义对于刚接触近世代数的学生来说较抽象,而高等代数中的多项式、矩阵、向量空间及有限维向量空间上的线性变换等为群提供了丰富的例子。例如,复数域C上全体n阶可逆矩阵关于矩阵的乘法构成群 (称为一般线性群),C上行列式为1的n阶矩阵全体关于矩阵的乘法构成群(称为特殊线性群),和C上n维向量空间的可逆变换关于线性变换的合成构成群等。以下通过具体的例子说明高等代数在群论中的应用。
例1:在 中,
试计算 的阶。
分析:矩阵 的阶直接计算可得。注意到矩阵AB的阶通过直接计算行不通,可运用高等代数的知识解决。
解:首先,直接计算可得
其中E为单位矩阵,故矩阵A的阶为3,矩阵B的阶为4。下面讨论矩阵AB的阶。有
容易算出,AB的特征多项式
显然, 也是AB的极小多项式。如果AB是有限阶的,则存在正整数n,使 。从而 是AB的零化多项式,于是应有
(1)
另一方面, 有重根 ,而 至多是 的单根,所以 不能整除 ,与(1)式矛盾,这说明AB不可能是有限阶的,即AB的阶为无限。
例2:试证一般线性群 不含有指数有限的真子群。
证明:反证法。假设H是 的指数有限的真子群,且 ,其中 为H在G中的指数。考虑G在H的左陪集集合上的左诱导作用,则有群同态
其中 为m次对称群,则有 , 为群同态 的核, 为商群 中元素个数。设 。一方面,对于任一 ,有 。另一方面,由高等代数知,对于任一 和任意正整数t,存在 使得 。因此,对于任一 ,有 。于是 ,即 ,矛盾!证毕。
3. 在环论中的应用
环是一类具有两种运算的代数系统。高等代数中复数域C上的全体多项式的集合 ,C上全体n阶方阵的集合以及C上向量空间的全体线性变换的集合关于通常的加法和乘法都构成环。此外,环论中唯一分解整环推广了算术基本定理,欧几里得整环推广了带余除法定理,主理想整环推广了最大公因子的表示定理。以下通过具体的例子说明高等代数在环论中的应用。
例3: 为 的极大理想。
证明:在 中,设I为任一真包含 的理想。在I中任取一个不属于 的多项式 ,由高等代数带余除法知存在 ,,使
从而
因 ,从而 不全为零。若 ,则 ,且
则

由此得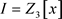 。若
。若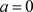 ,则
,则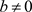 且
且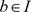 ,于是
,于是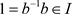 ,从而
,从而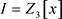 。证毕。
。证毕。
例4:如果 是整环D的中两两相异的
是整环D的中两两相异的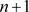 个元,
个元, 是D中任意
是D中任意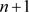 个元,则在
个元,则在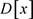 中至多存在一个次数小于等于n的多项式
中至多存在一个次数小于等于n的多项式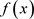 ,使得
,使得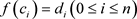 。
。
证明:只需证明:若有一个次数小于等于n的多项式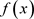 ,使得
,使得 ,则
,则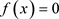 。
。
设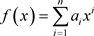 具有这种性质,则
具有这种性质,则
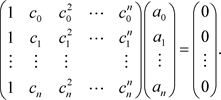
用A代表这个系数矩阵,则A是Vandermonde矩阵,因 两两相异,故
两两相异,故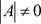 。从而,
。从而,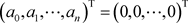 ,即
,即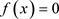 ,证毕。
,证毕。
注:当D为域时,上述多项式是存在的且能唯一表示出来。
4. 在域论中的应用
域是许多数学分支研究的基础,研究域最基本的方法是对域进行扩张。设E为F的扩域,则域E可以看作其子域F上的向量空间,则高等代数中向量空间的概念、理论与方法都可以移植到域上。下面通过具体的例子说明高等代数在域论中的应用。
例5:设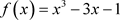 。
。
1) 证明: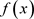 在有理数域Q上不可约。
在有理数域Q上不可约。
2) 若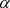 为
为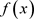 的一根,试求单扩域
的一根,试求单扩域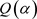 中元素
中元素 用
用 表示的线性表达式;再求
表示的线性表达式;再求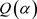 中元素
中元素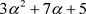 在
在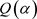 中的逆元。
中的逆元。
证明:1) 若 在Q上可约,则由高等代数知必在整数环Z上可约,从而有整数根,且此整数根是1的因数,即只能是
在Q上可约,则由高等代数知必在整数环Z上可约,从而有整数根,且此整数根是1的因数,即只能是 。但显然
。但显然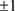 都不是
都不是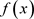 的根,因此
的根,因此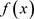 在有理数域Q上不可约。
在有理数域Q上不可约。
2) 由于 为
为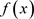 的一根,故
的一根,故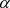 是Q上的3次代数元,且
是Q上的3次代数元,且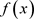 是
是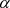 在Q上的最小多项式。因此,
在Q上的最小多项式。因此,
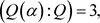
且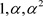 为
为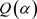 在Q上一组基。令
在Q上一组基。令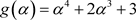 ,并用
,并用 去除
去除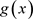 ,得
,得
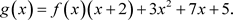
由于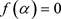 ,故由上式得
,故由上式得
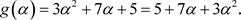
这就是 用
用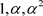 表示的线性表示式。
表示的线性表示式。
再令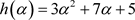 ,由于
,由于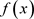 在Q上不可约,故显然
在Q上不可约,故显然
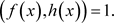
于是存在Q上多项式 使
使
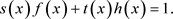 (2)
(2)
根据高等代数中的辗转相除法,易知

将 代入(2)式,由于
代入(2)式,由于 ,故可知
,故可知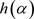 在
在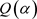 中的逆元是
中的逆元是
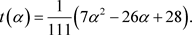
5. 总结
综上,高等代数不仅为近世代数提供了直观的例子,而且更能对其中的问题进行实质刻画,很多问题都可以利用高等代数的知识解决。本文只是给出高等代数在近世代数中的几点应用,更多的应用仍值得进一步研究。在近世代数教学中,将这种学科之间的紧密联系展现给学生,会极大地激发学生的学习兴趣和积极性,从而提高教学质量和教学效果。
基金项目
本文工作得到国家自然科学基金项目(11801363)和上海海事大学文理学院重点课程建设项目(2018) 资助。
文章引用
陈秋帆. 浅谈高等代数在近世代数教学中的应用
A Brief Discussion on Applications of Advanced Algebra in Modern Algebra Teaching[J]. 创新教育研究, 2020, 08(02): 104-108. https://doi.org/10.12677/CES.2020.82017
参考文献
- 1. 张禾瑞. 近世代数基础[M]. 北京: 高等教育出版社, 1978.
- 2. 韩士安, 林磊. 近世代数[M]. 第2版. 北京: 科学出版社, 2009.
- 3. 刘绍学. 近世代数基础[M]. 第2版. 北京: 高等教育出版社, 2012.
- 4. 冯克勤, 章璞. 近世代数三百题[M]. 北京: 高等教育出版社, 2010.
- 5. 万哲先. 代数和编码[M]. 北京: 科学出版社, 1980.
- 6. 阮传概, 孙伟. 近世代数及其应用[M]. 第2版. 北京: 北京邮电大学出版社, 2005.
- 7. 罗守山, 陈萍. 近世代数及其应用[M]. 北京: 北京邮电大学出版社, 2016.
- 8. 吕恒, 徐海静. 关于近世代数中群论学习的探讨[J]. 西南师范大学学报, 2012, 37(2): 131-133.
- 9. 武利猛, 张娟, 郑国萍, 等. 关于近世代数的几点教学体会[J]. 教育教学论坛, 2017(16): 205-206.
- 10. 北京大学数学系. 高等代数[M]. 北京: 高等教育出版社, 1988.
- 11. 丘维声. 高等代数[M]. 北京: 高等教育出版社, 2002.