Pure Mathematics
Vol.
08
No.
06
(
2018
), Article ID:
27839
,
7
pages
10.12677/PM.2018.86098
On the Minor Minimal Super 5-Connected Graphs
Chengfu Qin, Fenmei Mo*
Department of Mathematics and Statistics, Guangxi Teachers Education University, Nanning Guangxi

Received: Nov. 10th, 2018; accepted: Nov. 23rd, 2018; published: Nov. 30th, 2018

ABSTRACT
A graph H is called a minor of a graph G if H can be formed from G by deleting edges and vertices and by contracting edges. Let G be a k-connected graph such that G contains no other k-connected graph as its minor, then we call G a minor minimal k-connected graph. M. Kriesell showed that every minor hyper-5 connected graph has at most 12 vertices. In this paper, we show that every minor super-5 connected graph has at most 12 vertices.
Keywords:Super 5-Connected, Minor, Minimal, Characterization
子式极小的Super-5连通图
覃城阜,莫芬梅*
广西师范学院,数学与统计科学学院,广西 南宁

收稿日期:2018年11月10日;录用日期:2018年11月23日;发布日期:2018年11月30日

摘 要
如果图G可以经过去边,或者去点,或者收缩子图得到子图H,则称H是G的子式。若G是k-连通图且G中不包含另外一个k-连通图作为子式,则称G是子式极小的k-连通图。M. Krisesell证明了子式极小的hyper-5连通图的顶点数至多是12。本文将这个结论推广到Super-5连通图。
关键词 :Super-5连通图,子式,极小,刻画

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中我们考虑的都是有限阶,无向的简单图,未经说明的术语和记号我们参考 [1] 。设
,其中
是G的顶点集,
是G的边集。记
。若图G的任意顶点x与y都有连接x与y的路,则称G是连通图,否则G是不连通图,用
表示G的连通度。对于连通图G,
且
至少有两个分支,则称T是G的一个点割。若T是G的点割并且
,则称T是G的最小点割。设G是连通图,
是G的最小点割。若A是
若干个分支的并且
,则称T是A的断片。
在图G中与顶点x相邻的顶点称为x的邻点,x的所有邻点组成的集合称为x邻域,记为
。设
,记
。我们用
表示点x的度数,用
表示图G中所有度
数为k的顶点的集合。用
表示图G中的最大度,
表示图G中的最小度。
,我们用
表示集合S的诱导子图。
设
是图G的一条边,引进一个新的顶点
使其与x和y的所有邻点都相邻,最后将x和y的去掉所得到的图称为是由图G收缩边e所得到的图,记为G/xy。设G是k-连通图,
是图G的一条边。若G/xy还是k-连通图,则称e是G的k-可收缩边。若G是k-连通图且G的任意一条边e都有G/e不是k-连通图则称G是收缩临界k-连通图。若A是一个断片使得
中包含
,则称A是相对于F的断片。特别地,当
则称A是相对于e的断片.
由定义我们可知G是收缩临界k-连通图当且仅当对于任意
都有e包含在一个最小点割内。
T是连通图G的最小点割,我们称T是一个shredder如果
至少有3个分支。用
表示所有图G中的集shredder合。设
,设
有k个分支
。不失一般性,
。记
。
一个k-连通图G如果满足:对于任意的最小点割T,
有一个分支是孤立点,则称G是Super-k连通图,简称G是Super的。若G是Super的且G中没有shredder,则称G是的hyper-k连通图。
我们可以将收缩边的概念作如下推广:对于k-连通图G的子图H,收缩H使指将H的每一个连通分支的边逐一收缩成一点,所得到的图记为G/H。若G/H仍是k-连通图,我们称H是G的k-可收缩子图。
对于图G和H,如果G可以经过如下一系列运算得到H:1) 去边;2) 去点;3)收缩子图,则称H是的子式G。若G是k-连通图且G不能通过上述的三种运算得到另一个k-连通图,则称G是子式极小的k-连通图。由定义可知,G是子式极小的k-连通图,则G一定是极小的k-连通图且也是收缩临界k-连通图。M. Kriesell证明了如下结论。
定理1.1 [2] :设G是子式极小的5-连通图,若G是hyper5-连通图,则G最多有个12个顶点。
本文我们对收缩临界5-连通图的最小点割结构进行了研究,推广了M. Kriesell的结论,证明了如下结论。
定理1.2:设G是子式极小的5-连通图,若G是Super 5-连通图,则G最多有个12个顶点。
2. 定义与引理
我们知道子式极小的3-连通图是
,子式极小的4-连通图是
和
,而子式极小的5-连通图有哪些目前还尚不清楚,而且要确定这些图也是比较困难。
引理2.1 [3] :设G是收缩临界5-连通图,
,。若
且
,则
。
引理2.2 [3] :设G是收缩临界5-连通图,
,A是G中的断片且
。
若
, 并且
,则有
存在一个5度点z与x相邻,而且满足
且
。特别地,当
时,则有
。
引理2.3:设G是收缩临界5-连通图,
是G的一个断片。令B是相对于xz断片,这里
。如果
,则有
。
引理2.4 [4] :设G是收缩临界5-连通图,A是G的一个断片,使得
且有一个6度点,则
至少有三个5度点。
引理2.5 [4] :设G是收缩临界5-连通图,
,令
。若A为
-原子,则
。
引理2.6 [4] :设G是收缩临界5-连通图且
, 是G的断片,
。若
,,则
。
引理2.7 [4] :设G是收缩临界5-连通图,
,若
有一个元素的阶至少为2,则
的每个元的阶至少为4。
引理2.8 [5]:设G是收缩临界5-连通图,
表示G中的5度顶点的集合。设T是G的最小点割,A是T-断片且
。如果T中存在
,使得
,则T中存在一点
,使得
或者
与t相邻且
。
引理2.9 [4] :设G是子式极小5-连通图且
,则
无边导出子图。
引理2.10 [4]:设G是收缩临界5-连通图,设A为G的断片,
且
。若
,则
中包含x的一个5度点邻域。
引理2.11 [4] :设G是收缩临界k-连通图,R是shredder,令
,使得
。设
,,则
仍是收缩临界k-连通图。
在本文的证明中,我们会反复用到下面断片的结论:
引理2.12 [6] :若A,B为G的两个不同的断片,
,,那么:
1) 若
,则
, ;
2) 若
,则
和
都是G的断片,且
;
;
3) 若 ,且
不是断片,则有
,且
,。
,且
不是断片,则有
,且
,。
引理2.13 [4] :设A为G的断片,
。若
, 则A = N(S)。
3. 主要结果证明
引理3.1:设G是收缩临界5-连通图,
, 是G的断片,
,。令
,则
1)
;
2)
, ;
3) H中没有长为3的路;
若
,则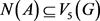 ,
。
,
。
证明:1) 由引理2.4,知
中至少有三个5度点。不妨设
。若
,我们将导出矛盾。
断言1:
,。
我们只证明
。对于
也可以类似证明。
如若不然,设
不与
中的5度点相邻。设
是相对于
的断片。由引理2.3,我们有
。又由假设,我们有
。不失一般性,设
。于是
在
中不与5度点相邻。令
是相对于
的断片,同样由引理2.3,知
。类似地,我们有
。不失一般性,设
。
若
,考察
,我们有
,, 且
,。由引理2.12可知
和
都是G的断片。所以
,由引理2.3,
。于是
,矛盾。
若
,不失一般性设
。此时考察
,我们同样可得
,矛盾。所以断言1成立。
不妨设
。若
,则
且
。注意到
,由引理2.2,
或
,矛盾。所以
,不妨设
。
断言2: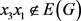 且
。
且
。
不妨设
,则
,。由引理2.2,知
, 且
。令
是相对于
的断片,显然有
。注意到
,,我们有
。于是
。这与
是长为2的路,矛盾。所以
,类似地
。
由引理2.10,有
。于是
, 且
,,由引理2.2可以导出矛盾。于是1)成立。
类似于引理2.6的证明,我们有2)的成立。由1)不妨设
。
下面我们来证明3)。反证法,不妨设
是H中长为3的路,则
,。此时我们主要到
,。由引理2.2,我们知
,。此时显然
在
中没有邻点。
令
是相对于
的断片,易见
。由于
在
中没有邻点,有
。这与
是H中长为3的路,矛盾。所以3)成立。
由2),我们设
和
是H的两条边。由3),
与
之间没有边。即
。所以当
时我们有
且
,故4)成立。于是引理3.1成立。
故对G收缩临界5-连通图,
, 是G的断片,
,,则由引理3.1,不妨设
且
,。此时易见
与
之间没有边。
若
是连通图,则由引理3.1,我们有
, 是路且易见
是
的中心。
若
有两个分支,不妨设
是其中一个分支,则另一个分支也是一条路。
由上面的结论,我们取H中的一条边,不妨设为
,使得
与
之间的边尽可能的少。于是若
与
之间有边,则其与
之间也有边。
引理3.2:令
,则
是5-连通图。
证明:令
是G分别收缩
后得到的新顶点。
断言1
。
若
与
之间没有边,则易见
。
若
与
之间有边,则由
的选择,我们不妨设
,。此时
,这里
是一条路。同样可得
。
断言2:
且
时,
包含在
的每一个最小点割内。
若
,令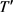 是阶为3的最小断片。由
,我们有
。令
是
的
-断片。由
,我们有
,。令T是将
恢复后所得到的集合。显然,
,。另外易见
是G中的
-断片。所以
。于是由
可知
或
。不妨设
。此时由
,我们有
,。则由引理2.1,
,矛盾。所以
。
是阶为3的最小断片。由
,我们有
。令
是
的
-断片。由
,我们有
,。令T是将
恢复后所得到的集合。显然,
,。另外易见
是G中的
-断片。所以
。于是由
可知
或
。不妨设
。此时由
,我们有
,。则由引理2.1,
,矛盾。所以
。
若
,令
是
的最小点割,
是
的
-断片。由于
,,。令T是将
恢复后所对应的集合。显然由
我们有
。若
,不妨设
。
令B是将
恢复后所对应的集合。显然可得,
,,。由
,我们有
,矛盾。所以断言2成立。
下面我们来证
。如若不然,令
是
的最小点割,
是
的
-断片。则由
,我们有
,。令T是将
恢复后所对应的集合。由断言2,
。于是
,。记
是
的一部分。这里为方便讨论,我们仍然记
。由
,我们有
,。由对称性,设
。下面分两种情况讨论。
情况1:
不连通。由
,则
,。此时有
以及
,,或者
。不妨设
,则
。于是
是G阶为4的点割,矛盾。
情况2:
不连通。
则由
的选择,
在
中没有邻点。
若
,则
。由
与
之间没有边,有
。于是
。
由
在
中没有邻点,有
,显然
且
。令
,则
,,。又由于
,我们有
,,。若
,由引理2.2可得到矛盾。
所以设
。注意到
,则
,。
与
之间没有边。若
,由引理2.2得,
,矛盾。
若
,则由引理2.8得,
与
之间没有边,矛盾。
所以设
。若
,令
。由
,以及
在
中没有邻点,我们有
。令
,显然易见
,。
令C是G的相对于
的断片,显然
。又由
在
中没有邻点,
。不妨设
,。由G是5-连通图我们有,
,。故
, 都是G的断片。所以
。此时易见
。我们不妨设
,。由
,。于是
。由引理2.1,
,。故
,。因此是
是G的4-点割,矛盾。
所以我们设
,。
注意到
。当
,则
是G的4-点割,矛盾。所以
,类似的有
。于是
,。若
,则B是G的断片,
。则有
,。此时对
和B应用引理2.2可导矛盾。所以
,类似地有
。于是
,。令
,则
,,。由
以及引理2.1,我们有
。若
,则由引理2.8,
中存在一个点与
或
相邻,矛盾。若
,对
和
应用引理2.2可导出矛盾。
引理3.3 设G是子式极小5-连通图,且
是5-shredder,则
,这里
。
证明:显然,G收缩临界极小5-连通图。令
是
的三个分支。若A,B或C中有一个阶为1,则结论成立。于是设
,,。由推论2.7,
的每一个分的阶至少为4。记
。令
,我们将证明
是5-连通图。这与G是子式极小,矛盾。
断言1:
。
否则
。由于
有至少三个断片,于是
至少有一个断片只含
的一个邻点。不妨设
,则由引理2.2,
中存在一个5度点,设为
,使得
且
。由
,我们有
,,。同样由引理2.2,
,。于是
,矛盾。所以断言1成立。
由引理2.9以及断言1,我们有
。
断言2:
在 的每个分支内至少有两个邻点。
的每个分支内至少有两个邻点。
否则不妨设
,则由引理2.2可知
中存在一个5度点,矛盾。
由断言1以及断言2,我们有
且
。令a将A收缩后得到的点。
下面我们来证明
。否则,设
是
中阶为4的点割,D是
的
-断片。由
,我们有
。
显然
。我们设
。于是有
, (否则,不妨设
,则
是
的一个断片且
,此时易见
是G的4点割,矛盾)。不妨设
,。由
是
的连通分支,我们有
和
都有路连接
和
且
。故
。
于是我们有
或
。不妨设
且
。此时由断言2,我们有
可以分成两子图
和
,使得
,。于是我们有
是G的一个4点割,矛盾。
推论3.1:设G是子式极小的5-连通图且有
。则对任意最小点割T,则
恰好有两个分支。特别的,若G还是Super5-连通,则G一定是hyper5-连通。
证明:由定义,G是收缩临界的极小5-连通图。若
有至少3个分支。令A,B和C是
的3个分支。由引理2.7和引理3.3我们有
恰好有3个分支且有两个分支只有一个点。不妨设
,,。由引理2.10,
仍然是收缩临界5-连通图。于是在
中,
是
的一个断片,且x和y在
中的度为6。设
,我们如引理3.2选取
。则由引理3.2,
是5-连通图。又
,我们有
,这与G是子式极小,矛盾。于是
恰好有两个分支,当G还是Super5-连通,显然可知,G是hyper5-连通。
由定理1.1以及推论3.1,我们可知定理1.2成立。
基金项目
国家自然科学基金资助项目:11401119。
文章引用
覃城阜,莫芬梅. 子式极小的Super-5连通图
On the Minor Minimal Super 5-Connected Graphs[J]. 理论数学, 2018, 08(06): 730-736. https://doi.org/10.12677/PM.2018.86098
参考文献
- 1. Bondy, J.A. and Murty, S.R. (1976) Graph Theory with Alications. MacMillan.
- 2. Kriesell, M. (2007) How to Contract an Essen-tially 6-Connected Graph to a 5-Connected Graph. Discrete Mathematics, 307, 494-510.
https://doi.org/10.1016/j.disc.2005.09.040
- 3. 覃城阜. 收缩临界5-连通图的性质[D]: [硕士学位论文]. 桂林: 广西师范大学, 2004.
- 4. 覃城阜. 5-连通图的可收缩子图及minors [D]: [博士学位论文]. 厦门: 厦门大学, 2010.
- 5. Kriesell, M. (2005) Triangle Density and Contractibility. Combinatorics, Probability and Computiny, 14, 133-146.
- 6. Kriesell, M. (2001) A Degree Sum Contio for the Existence of Contraciable Edge in k Connected Graph. Journal of Combinatorial Theory, Series B, 82, 81-101.







 ,且
不是断片,则有
,且
,。
,且
不是断片,则有
,且
,。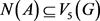 ,
。
,
。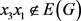 且
。
且
。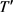 是阶为3的最小断片。由
,我们有
。令
是
的
-断片。由
,我们有
,。令T是将
恢复后所得到的集合。显然,
,。另外易见
是G中的
-断片。所以
。于是由
可知
或
。不妨设
。此时由
,我们有
,。则由引理2.1,
,矛盾。所以
。
是阶为3的最小断片。由
,我们有
。令
是
的
-断片。由
,我们有
,。令T是将
恢复后所得到的集合。显然,
,。另外易见
是G中的
-断片。所以
。于是由
可知
或
。不妨设
。此时由
,我们有
,。则由引理2.1,
,矛盾。所以
。 的每个分支内至少有两个邻点。
的每个分支内至少有两个邻点。