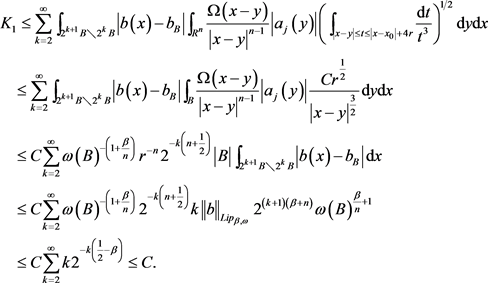Pure Mathematics
Vol.
10
No.
05
(
2020
), Article ID:
35794
,
10
pages
10.12677/PM.2020.105068
Double Weighted Estimates for the Commutator of Marcinkiewicz Integral with Some
Kernel
Yingting Ji, Xiaoli Chen
College of Mathematics & Information Science, Jiangxi Normal University, Nanchang Jiangxi

Received: Apr. 27th, 2020; accepted: May 20th, 2020; published: May 27th, 2020

ABSTRACT
In this paper, we obtain that the commutator
generated by Marcinkiewicz integral
with
kernel and weighted Lipschitz function b, has
and
boundedness.
Keywords:Commutator, Marcinkiewicz Integral, Weighted Lipschitz Function,
Condition

具有某类
核函数的Marcinkiewicz积分交换子的双权估计
季颖婷,陈晓莉*
江西师范大学数学与信息科学学院,江西 南昌

收稿日期:2020年4月27日;录用日期:2020年5月20日;发布日期:2020年5月27日

摘 要
本文证明核函数满足
条件的Marcinkiewicz积分
与加权Lipschitz函数b生成的交换子
具有
和
有界性。
关键词 :交换子,Marcinkiewicz积分,加权Lipschitz函数,
条件

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设
是
上的单位球面且具有标准的Lebesgue测度,
是
上的零次齐次函数且满
足:对任意的
,
(1.1)
定义Marcinkiewicz积分算子为
由Marcinkiewicz积分
和适当的函数b生成的交换子定义为
如果存在常数
和
,使得对任意的
,有
(1.2)
则称
满足log型Lipschitz条件。
Marcinkiewicz首先在文 [1] 中给出了一维Marcinkiwicz算子
的定义,此时
。1958年,Stein在 [2] 中定义了高维的Marcinkiewicz积分,并证明当
时,
是强
型和弱
型的。2004年,Lee和Rim在 [3] 中引入log型Lipschitz条件(1.2),并证明当
满足(1.2)时Marcinkiewicz积分
的
和
有界性。显然条件(1.2)比Stein定理中的Lipschitz条件更弱。关于Marcinkiewicz积分算子有界性的结果很多,范大山、陈杰诚、丁勇、陆善镇和Yabuta等人在这一领域做出了巨大贡献,文献较多就不一一枚举。
对于Marcinkiewicz积分交换子,Torchinsky和Wang在 [4] 中证明当核函数满足Lipschitz条件时Marcinkiewicz积分和它的交换子在加权
上有界,Ding、Lu和Yabuta在 [5] 中讨论带粗糙核的Marcinkiewicz积分与BMO函数生成的高阶交换子的加权有界性。Ding、Lu和Zhang [6] 建立了Marcinkiewicz积分交换子的
有界性。2008年,王、张和刘 [7] 给出核函数满足条件(1.2)时,Marcinkiewicz积分交换子在Hardy空间上的端点估计。Lin、Liu和Wang [8] 将 [7] 的结果推广到加权情形。另一方面,陆、吴和杨 [9] 研究了奇异积分算子和Lipschitz函数生成的交换子在Hardy空间上的端点估计。
如果存在常数
和
,使得对任意的
,有
(1.3)
则称
满足
条件。条件(1.3)比log型Lipschitz条件(1.2)弱。当
时,
条件即为log型Lipschitz条件。Wang在文 [10] 中讨论变量核的参数型Marcinkiewicz积分算子
,得到核函数满足消失性条件和
条件时,
在Hardy空间
和弱Hardy空间
上的有界性。
受文献 [7] [8] 和 [9] 的启发,我们将研究核函数满足
条件(1.3)时,Marcinkiewicz积分算子和加权Lipschitz函数生成的交换子在加权Hardy空间上的有界性。具体地,即建立Marcinkiewicz积分
交换子
的
和
有界性。为此,首先给出本文的一些基本定义。
定义1.1 设
为一个权函数,
。若一个局部可积函数
满足
其中上确界取遍所有的球
。则称b属于加权Lipschitz空间,记为
。上式中C的最小下确界称为b的
范数,记为
。对不同的
和
,函数b的
和
等价,因此通常可以记b的加权Lipschitz范数为
,见文献 [11]。
本文结果如下。
定理1.1 设
以及
满足光滑性条件(1.3)。若
且
。
则
是
到
上的有界算子。
定理1.2 设
以及
满足光滑性条件(1.3)且
。则交换子
是
到
有界的。即对任意的
,存在常数
,使得
2. 预备知识和相关引理
这节介绍一些我们所需的概念和引理。先给出
权的定义。
定义2.1 设
。如果对任意
,存在常数
使得
则称权函数
。如果存在常数
,使得
,则称权函数
。
下面介绍加权Hardy空间的概念及原子分解。
定义2.2 记S为Schwartz函数类,
是它的对偶。设
, 为权函数。定义 的极
的极
大函数
。加权Hardy空间定义为
且记
。
定义2.3 设
是一个权函数,
。a是一个有界的可测函数,如果它满足下面的条件
(i) 存在一个球B使得 ;
;
(ii)
;
(iii)
,
则称a为加权的p-原子,球B为原子a的支集球。设f为缓增广义函数。如果在分布意义下f可以写成
,这里
是p-原子,N为任意的整数,
且
,则称f属于原子加权Hardy
空间
,并定义
中的半范为
其中下确界“inf”是对f的一切分解取的。
引理2.1 [12] 设
,则对于球B的任意可测子集E,存在常数
和
,使得
成立。如果
是常值函数,则
;如果
不是常值函数,则
。
引理2.2 [5] 设
是一个零次齐次函数且满足条件(1.1)。若
和
满足下列条件之一:
(i)
和
;
(ii)
和
;
(iii)
和
,
则
在
上有界。
引理2.3 [13] 设
,则
引理2.4 设
,则
证明 利用Hölder不等式,引理2.3和引理2.1可得
引理2.5 [14] 设
。设
且
,则
是 到
上的有界算子。
到
上的有界算子。
3. Marcinkiewicz积分交换子在加权Hardy空间上的有界性
下面给出Marcinkiewicz积分交换子的
和
有界性证明。
定理1.1的证明 由于
是次线性算子,所以只需要证明对每一个加权p-原子
,有不等式
(3.1)
若(3.1)成立,由于
,则对f的任意分解
,利用定义2.3 (ii)
可得
下面证明(3.1)。设
,则
取
且
。利用Hölder不等式,引理2.5和定义2.3 (ii)可得
对于
,有
而对于
,有
接下来首先估计
。当
时有
,因此有
(3.2)
且
(3.3)
因此有
(3.4)
利用Minkowski不等式,(3.2)式,零次其次函数
和引理2.3可得
接着估计
。利用原子
的消失性,Minkowski不等式,(3.4)和引理2.3可得
这里最后一个不等式用到
和
,从而级数收敛。最后估计
。利用引理2.2 (i),定义1.2,定义
2.3 (ii)以及
可得
结合
的估计可得(3.1)。定理证毕。
定理1.3的证明 记
,其中aj是
原子且满足
。则
利用Hölder不等式,引理2.2 (i),定义1.1,
是
原子和引理2.3可得
对于
,有
接下来我们分别估计
和
。首先对于
,我们利用Minkowski不等式,(3.2)式,定义2.3 (ii)和引理2.4可得
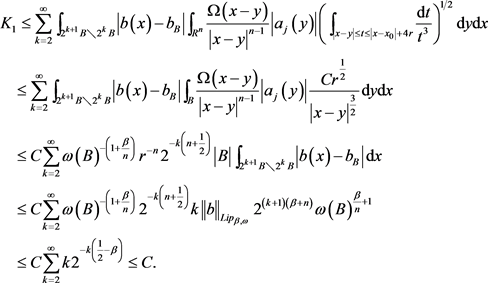
接着估计
,利用原子
的消失性,Minkowski不等式,(3.4)和引理2.3可得
其中最后一个不等式利用了
从而级数收敛。因此
最后,利用引理2.7,定义2.1和定义2.3 (ii),有
综上,由
和
的估计可得
再对f的所有原子分解取下确界,即可完成定理的证明。
基金项目
江西省自然科学基金(项目编号: 20192BAB201003)。
文章引用
季颖婷,陈晓莉. 具有某类Lδ-(logL)ρ核函数的Marcinkiewicz积分交换子的双权估计
Double Weighted Estimates for the Commutator of Marcinkiewicz Integral with Some Lδ-(logL)ρ Kernel[J]. 理论数学, 2020, 10(05): 556-565. https://doi.org/10.12677/PM.2020.105068
参考文献
- 1. Marcinkiewicze, J. (1938) Sur quelques intégrals de type de Dini. Annales Polonici Mathematici, 17, 42-50.
- 2. Stein, E.M. (1958) On the Function of Littlewood-Paley, Lusin and Marcinkiewicze. Transactions of the American Mathematical Society, 88, 430-466.
- 3. Lee, J. and Rim, K.S. (2004) Estimates of Marcinkiewicze Integral with Bounded Homogeneous Kernel of Degree Zero. Integral Equations and Operator Theory, 48, 213-223. https://doi.org/10.1007/s00020-001-1193-1
- 4. Torchinsky, A. and Wang, S. (1990) A Note on the Marcinkiewicze Integral. Colloquium Mathematicum, 60/61, 235-243.
- 5. Ding, Y., Lu, S.Z. and Yabuta, K. (2002) On Commutator of Marcinkiewicze Integral with Rough Kernel. Journal of Mathematical Analysis and Applications, 275, 60-68.
- 6. Ding, Y., Lu, S.Z. and Zhang, P. (2004) Weighted Weak Type Estimates for Commutators of Marcinkiewicz Integrals. Science in China, 47, 83-95. https://doi.org/10.1360/03ys0084
- 7. 王洪彬, 张小瑾, 刘宗光. 一类Marcinkiewicz积分交换子的端点估计[J]. 数学学报A辑, 2008, 51(2): 265-274.
- 8. Lin, Y., Liu, Z.G. and Wang, D. (2012) Weighted Endpoint Estimate for Commutator of Marcinkiewicze Integral. Pan-American Mathematical Journal, 22, 105-116.
- 9. 陆善镇, 吴强, 杨大春. 交换子在Hardy空间上的有界性[J]. 中国科学A辑, 2002, 32(2): 232-244.
- 10. Wang, H. (2016) Estimates of Some Integral Operators with Bounded Variable Kernels on the Hardy and Weak Hardy Spaces over Rn. Acta Mathematica Sinica, English Series, 32, 411-438. https://doi.org/10.1007/s10114-016-4617-1
- 11. Carcia-Cuerva, J. and Rudio De Francia, J.L. (1958) Weighted Norm Inequalities and Related Topics. North-Holland Math, Amsterdam. https://doi.org/10.1016/s0304-0208(08)73086-x
- 12. Garca-Cuerva, J. (1979) Weighted Hp Space. Dissertation Summaries in Mathematics, 162, 1-63.
- 13. 黄菲. Marcinkiewicz~积分交换子和多线性平方算子交换子的有界性[D]: [硕士学位论文]. 南昌: 江西师范大学, 2017.
- 14. 李爽. Marcinkiewicz积分及其交换子的加权范数不等式[D]: [硕士学位论文]. 南昌: 江西师范大学, 2018.
NOTES
*通讯作者。








 的极
的极 ;
; 到
上的有界算子。
到
上的有界算子。