Operations Research and Fuzziology
Vol.
14
No.
02
(
2024
), Article ID:
84298
,
9
pages
10.12677/orf.2024.142125
星图相关矩阵的Moore-Penrose广义逆
王玉浩
长安大学理学院,陕西 西安
收稿日期:2024年1月14日;录用日期:2024年2月4日;发布日期:2024年4月11日

摘要
本文利用矩阵的低秩性、分块性等性质给出了星图的邻接矩阵、关联矩阵、距离矩阵、拉普拉斯矩阵和无符号拉普拉斯矩阵的Moore-Penrose广义逆。以上结论对进一步研究星图的代数性质提供了理论支撑,同时对研究其他图类的相关矩阵的广义逆提供了理论参考。
关键词
星图,分块矩阵,Moore-Penrose广义逆

Moore-Penrose Inverses of the Related Matrices of Star Graphs
Yuhao Wang
School of Science, Chang’an University, Xi’an Shaanxi
Received: Jan. 14th, 2024; accepted: Feb. 4th, 2024; published: Apr. 11th, 2024

ABSTRACT
Based on the properties of the low rank, partitioned matrix structure, we give the explicit form for the Moore-Penrose inverse of the adjacency matrix, incidence matrix, distance matrix, Laplacian matrix and signless-Laplacian matrix of star graphs, which provides theoretical support for further study of the algebraic properties of star graphs and theoretical aid for the study of the generalized inverse for matrices of other graphs.
Keywords:Star Graph, Block Matrix, Moore-Penrose Inverse

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设图G是一个无向简单图,其顶点集为 ,边集为 。图G的邻接矩阵 ,其中:当顶点 与 相邻时, ;反之 。图G的点边关联矩阵 ,当顶点 与 关联时, ;反之 。图G的距离矩阵 ,其中 表示顶点 与 之间的最短距离。图G的度矩阵 ,其中 表示顶点 的邻点数。图G的拉普拉斯矩阵 。图G的无符号拉普拉斯矩阵 。
设图 是一个有向简单图,其顶点集为 ,边集为 。定义图 的点边关联矩阵 ,当顶点 是有向边 的起点时, ;当顶点 是有向边 的终点时, ;反之 与 不关联时, 。
对任意的 ,如果存在 ,满足下面4个条件:
则称X是A的Moore-Penrose广义逆矩阵 [1] ,记为 。当矩阵A可逆时,容易证得 ;当A为行满秩矩阵时,有右逆 ,为列满秩矩阵时,有左逆 ,容易证明此时A的左逆或右逆就是A的Moore-Penrose广义逆。反之当A既不行满秩又不列满秩时可以使用满秩分解和奇异值分解去求解 ,但事实上,使用上述两种方法得到的广义逆的表示形式可能非常复杂,图的相关矩阵对于研究图的性质有关键作用,因此给出图矩阵广义逆的简洁表示形式是非常有意义的。
近几十年来,图相关矩阵的广义逆的研究受到了广泛关注,Bapat等人给出了距离正则图和完全多部图的关联矩阵的Moore-Penrose广义逆,接着又给出了偶数个顶点的轮图的距离矩阵的求逆公式,详见文献 [2] [3] [4] 。Hessert和Mallik给出了图的无符号拉普拉斯矩阵和边拉普拉斯矩阵的Moore-Penrose广义逆 [5] ,接着又给出了单圈图关联矩阵的逆 [6] 。Alazemi等人考虑对对称矩阵A进行公平划分,得到了
的充分条件,从而利用 重构出 ,极大地简化了Moore-Penrose广义逆的求解 [7] 。本文依据星图相关矩阵的结构特点,利用分块矩阵给出了星图邻接矩阵、关联矩阵、距离矩阵、拉普拉斯矩阵以及无符号拉普拉斯的Moore-Penrose广义逆的具体表示形式,对进一步研究星图的代数性质提供了理论支撑,同时对研究其他图类的相关矩阵的广义逆提供了理论参考。
2. 预备知识
设A为实数域上的n阶分块矩阵,分块划分为 ,其中每一个 均为非空不交集合,且有 ,矩阵A的每一块 ,即:
令 为划分 对应的商矩阵, 中的元素 等于分块矩阵 的平均行和。如果矩阵A的每一个分块 每一行的和都等于这个分块矩阵的平均行和,则称划分 是矩阵A的一个公平划分。
定理2.1指出对于对称矩阵A,如果 是矩阵A的一个公平划分,则 也是A的Moore-Penrose广义逆矩阵 的一个公平划分。
定理2.1 [7] 设 且 , 是矩阵A的一个公平划分,对应的商矩阵为 ,且 。则 也是 的一个公平划分,对应的商矩阵
引理2.1给出了一个 和 等价的充分条件。
引理2.1 [7] 设A是一个对称矩阵, 是矩阵A的一个公平划分,对应的商矩阵为 。如果 可逆,则 也可逆且 。
引理2.2~2.4给出了Moore-Penrose广义逆的相关性质和计算公式。
引理2.2 [8] 设 , 为矩阵A的Moore-Penrose广义逆,则有 。
引理2.3 [8] 设A是一个对称矩阵,则 或 也是对称矩阵。
引理2.4 [8] 设 ,且有满秩分解 ,其中 , 。则有 。
引理2.5给出了图的拉普拉斯矩阵、无符号拉普拉斯矩阵和关联矩阵之间的关系。
引理2.5 [9] 对于无向简单图G,给其每条边赋方向,记为图 ,则有
引理2.6给出了一种特殊的矩阵满秩分解方法。
引理2.6 [10] 设 , ,则矩阵A存在一个满秩分解 ,其中, , ,矩阵G为对A施行初等行变换后得到的行最简形矩阵的前r行,令 代表G每一行第一个1所在的列数,矩阵F为A的第 个列向量所构成的矩阵。
在下文的描述中, 代表长度为n的全1列向量, 代表n阶单位矩阵, 代表 阶全1矩阵, 代表 阶全0矩阵。
3. 主要结果
命题3.1 设A是实数域上的n阶对称矩阵,如果矩阵A的某些行(列)完全相同,即: ,其中 则 的那些行(列)对应也完全相同。
证明:由引理2.6,实数域上的n阶对称矩阵A存在一个满秩分解 ,其中矩阵G为对A施行初等行变换后得到的行最简形矩阵的前r行。假设矩阵A的第i行和第j行相等,对任意的 由于 且 ,有 。又因G为对A施行初等行变换后得到,故有 。由引理2.4,对任意的 , 的第i行和第j行元素
于是A的广义逆矩阵 的第i行和第j行元素对应相等,命题得证。
星图由一个顶点连上若干个孤立顶点得到,如下图G所示。给图G的每条边加上方向变为有向图,如下图 所示。
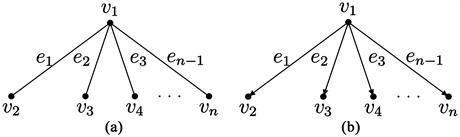
Figure 1. (a) Undirected star graph and (b) directed star graph
图1. (a) 无向星图 和(b) 有向星图
定理3.1给出了星图的邻接矩阵的Moore-Penrose广义逆的分块表示。
定理3.1 设 是一个有n个顶点的无向星图,则其邻接矩阵A的Moore-Penrose广义逆为
.
证明:根据图1中G的顶点标号,星图 的邻接矩阵有以下形式:
显然,矩阵A的后 行(列)相同。考虑对A进行分块划分,划分 。容易验证划分 是一个公平划分,对应的商矩阵
易得商矩阵 可逆且有
由定理2.1和引理2.1,划分 也是 的一个公平划分且有
由命题3.1, 的后 行(列)也相同,因此利用 重构出 如下:
定理得证。
定理3.2给出了星图的关联矩阵的Moore-Penrose广义逆的分块表示。
定理3.2 设 是一个有n个顶点的无向星图,则其关联矩阵M的Moore-Penrose广义逆为
.
证明:由图1中G的顶点及边的标号,其关联矩阵可记为
.
易证M为列满秩矩阵,故其有左逆,且 ,又 ,得
定理得证。
定理3.3给出了星图的距离矩阵的Moore-Penrose广义逆的分块表示。
定理3.3 设 是一个有n个顶点的无向星图,则其距离矩阵D的Moore-Penrose广义逆为
.
证明:根据图1中G的顶点标号,星图 的距离矩阵有以下形式:
,
通过计算其行列式易证距离矩阵D为可逆矩阵,因而 。令
,
则有
因而
将(1)代入(3)中,得 ,解得 ,代入(1)中有
,
得 , 。又因距离矩阵D为对称矩阵,由引理2.3, 也是对称矩阵,得 ,代入(4)中有
,
得 。因而
,
定理得证。
定理3.4给出了星图的无符号拉普拉斯矩阵矩阵的Moore-Penrose广义逆的分块表示。
定理3.4 设 是一个有n个顶点的无向星图,则其无符号拉普拉斯矩阵Q的Moore-Penrose广义逆为
.
证明:由引理2.2和引理2.5,得 , 。又由定理3.2得
,
故有
定理得证。
定理3.5给出了星图的拉普拉斯矩阵矩阵的Moore-Penrose广义逆的分块表示。
定理3.5 设 是一个有n个顶点的无向星图, 是对G的每条边赋方向的有向星图,则G的拉普拉斯矩阵L的Moore-Penrose广义逆为
.
证明:根据图1中 的顶点及有向边标号,得图 的关联矩阵H为
.
易证H为列满秩矩阵,故其有左逆,且 。又 ,得
由引理2.2和引理2.5,得 , ,故有
定理得证。
例3.1 如图2所示, 为8个顶点的无向星图, 是将 每条边赋方向后的有向星图。

Figure 2. (a) Undirected star graph ; (b) directed star graph
图2. (a) 无向星图 ;(b) 有向星图
由定理3.1~3.5,可以得到下表1结果:
Table 1. The related matrices and their Moore-Penrose inverses of star graph K 1 , 7
表1. 星图 的相关矩阵及其Moore-Penrose广义逆
4. 结语
图的相关矩阵对于研究图的代数性质有关键作用,本文借助分块矩阵给出了星图的邻接矩阵、关联矩阵、距离矩阵、拉普拉斯矩阵和无符号拉普拉斯矩阵的Moore-Penrose广义逆的具体结果,并给出了计算例子。后续将深入推广此方法,研究其他图类相关矩阵的Moore-Penrose广义逆。
文章引用
王玉浩. 星图相关矩阵的Moore-Penrose广义逆
Moore-Penrose Inverses of the Related Matrices of Star Graphs[J]. 运筹与模糊学, 2024, 14(02): 191-199. https://doi.org/10.12677/orf.2024.142125
参考文献
- 1. Ben-Israel, A. and Greville, T.N.E. (2003) Generalized Inverses: Theory and Applications. 2nd Edition, Springer, New York, 40-51.
- 2. Azimi, A. and Bapat, R.B. (2018) Moore-Penrose Inverse of the Incidence Matrix of a Distance Regular Graph. Linear Algebra and Its Applications, 551, 92-103. https://doi.org/10.1016/j.laa.2018.04.003
- 3. Azimi, A. and Bapat, R.B. (2019) The Moore-Penrose Inverse of the Incidence Matrix of Complete Multipartite and Bi-Block Graphs. Discrete Mathematics, 342, 2393-2401. https://doi.org/10.1016/j.disc.2019.05.007
- 4. Balaji, R., Bapat, R.B. and Goel, S. (2021) An Inverse Formula for the Distance Matrix of a Wheel Graph with an Even Number of Vertices. Linear Algebra and Its Applications, 610, 274-292. https://doi.org/10.1016/j.laa.2020.10.003
- 5. Hessert, R. and Mallik, S. (2021) Moore-Penrose Inverses of the Signless Laplacian and edge-Laplacian of Graphs. Discrete Mathematics, 344, Article ID: 112451. https://doi.org/10.1016/j.disc.2021.112451
- 6. Hessert, R. and Mallik, S. (2023) The Inverse of the Incidence Matrix of a Unicyclic Graph. Linear and Multilinear Algebra, 71, 513-527. https://doi.org/10.1080/03081087.2022.2035307
- 7. Alazemi, A., Anđelić, M. and Cvetković-Ilić, D. (2021) The Moore-Penrose Inverse of Symmetric Matrices with Nontrivial Equitable Partitions. Applied Mathematics and Computation, 400, Article ID: 126036. https://doi.org/10.1016/j.amc.2021.126036
- 8. 王松桂, 杨振海. 广义逆矩阵及其应用[M]. 北京: 北京工业大学出版社, 1996.
- 9. Cvetković, D., Rowlinson, P. and Simić, S. (2010) An Introduction to the Theory of Graph Spectra. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511801518
- 10. 程云鹏, 张凯院, 徐仲. 矩阵论[M]. 西安: 西北工业大学出版社, 2006: 220-225.
