Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18458,7
pages
10.12677/AAM.2016.53059
Bifurcation of Periodic Solution of a Hematopological System and Feedback Control
Suqi Ma
Mathematical Department, Chinese Agricultural University, Beijing

Received: Aug. 11th, 2016; accepted: Aug. 25th, 2016; published: Aug. 31st, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The oscillating phenomenon of a hematological cell model is investigated. Based on effective G-SCF administration, the mathematical blood cell model is described as DDEs with multi-delays. Commonly, in blood cell models, the intrinsic mechanism is composed of triggering differentiating mechanism and maturation mechanism, and hematoplogical cell model differentiating into three types of necessary blood cells in the body. By applying numerical software DDE-Biftool, the bifurcation of periodic solutions with long period are derived, and the period doubling bifurcation of periodic solutions is found at critical values. Chaotic solutions also appear afterwards period- doubling bifurcation, and the stabilization of dynamical chaos to the expected periodic solution is finished successfully by applying Pyragas feedback control method.
Keywords:Hematological Cell Model, Periodic Solution, Periodic Doubling Bifurcation, Delay

造血系统中的周期解分岔及反馈控制
马苏奇
中国农业大学数学系,北京

收稿日期:2016年8月11日;录用日期:2016年8月25日;发布日期:2016年8月31日

摘 要
本文研究了一类基于粒子集落刺激因子管理嗜中性粒子的血液病振荡数学模型。通常造血系统内部过程由激发分化机制和成熟机制两部分组成。造血干细胞分化得到了动物和人类必须的三类血液细胞:白细胞、红细胞和血小板。文中应用DDE-Biftool软件,数值模拟了造血系统中的长周期解的周期解分叉,得到了周期解的倍周期分叉。倍周期分叉后系统出现混沌解,应用反馈控制可以消除混沌或把系统稳定在期望的轨道上。
关键词 :造血系统,周期解,倍周期分叉,时滞

1. 引言
理解和研究造血系统对人类健康是非常必要的。造血干细胞分化能够得到动物和人类必须的三类血液细胞:白细胞、红细胞和血小板。而造血作用的失调会导致很多的血液学方面的疾病,如典型的例子有慢性的嗜中性白血球减少症。在病人中,一个或多个类型的血液循环细胞中出现明显的振荡。因而非线性动力学是研究血液病动力学的一个很好的工具。
通常造血系统由激发分化和增殖的机制以及成熟机制组成。从建模起,人们习惯于用Holling函数表达造血干细胞分化成为嗜中性粒子和自我更新的干细胞的数量。和组织细胞的相互作用中,细胞需要经历的成熟期一般为几天(2到6天),增殖放大的系数用指数形式表示。作为造血系统的一个极为明显的特征就是系统中引入了滞量,由于细胞的分化和成熟都需要一定的天数,所以系统是一多时滞模型,人们大都发展了包括造血干细胞房和嗜中性粒子细胞房在内的两房非线性反馈调控系统 [1] [2] 。
实验里,在人类血液病——周期性嗜中性粒子(CN)中,以振荡周期为19~21天几乎不能检测到嗜中性粒子为特征。在癌症治疗中,医学上一般使用集粒落刺激因子(G-CSF)来管理CN,其一般原理是降低嗜中性粒子前体细胞的程序性凋亡率 [3] [4] 。而动物实验中,在灰色利犬身上已发现了CN疾病,发现除振荡周期为11~15天外,其余与人类CN疾病几乎没有区别。在数学建模过程中,一些学者们基于G-CSF管理CN建立了周期性血液病的两房模型 [5] [6] 。应用非线性动力学工具,他们发现了造血系统中具有丰富的动力学现象,比如双稳态和周期解共存现象。
本文应用DDE-Biftool数学软件,研究了两房血液病模型的周期解分叉。模型中发现三类典型的长周期解,利用DDE-Biftool软件,分别追踪得到周期从46天左右演化为186天的倍周期解分叉,和周期为79天和周期为159天的吸引子的连续延拓。倍周期解是通往混沌的路径之一。利用Pyragas方法研究了混沌的反馈控制,发现负反馈增益可以使系统稳定在不同的周期轨道上,并且增益的连续改变带来了混沌系统的倍周期分叉现象。正反馈增益使得系统稳定在期望的吸引态。
2. 造血系统的两房数学模型
造血过程由激发分化机制和成熟机制两部分组成,具体地,造血干细胞经由细胞分裂分化成为全部血液细胞包括白细胞、红细胞和血小板,并能自我更新,形成了外周血液细胞的反馈调控环。基于G-CSF管理CN,考虑如下造血系统的两房模型
 (1)
(1)
其中Holling函数
 ,
,
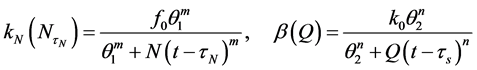
其生物学意义如下:干细胞以速率 进入其增殖相,并以速率
进入其增殖相,并以速率 进入嗜中性粒子房,以速率
进入嗜中性粒子房,以速率 分化成为其它血液细胞;嗜中性粒细胞耦合时滞为
分化成为其它血液细胞;嗜中性粒细胞耦合时滞为 ,由两部分的和构成,分别是其前驱细胞的增殖相需要的天数
,由两部分的和构成,分别是其前驱细胞的增殖相需要的天数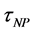 和成熟相需要的天数
和成熟相需要的天数 。
。 是增殖速率,
是增殖速率,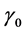 是成熟相中的死亡率。速率
是成熟相中的死亡率。速率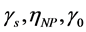 和成熟时间
和成熟时间 依赖于粒细胞集落刺激因子的管理。系统(1)有丰富的动力学现象 [5] 。
依赖于粒细胞集落刺激因子的管理。系统(1)有丰富的动力学现象 [5] 。
选取 为分叉参数。在模型(1)中,其估计的参数值列出如下
为分叉参数。在模型(1)中,其估计的参数值列出如下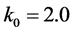 ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,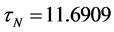 。
。
3. 数值模拟
3.1. 造血系统的吸引子及混沌
应用DDE-Biftool工具和DDE23,可以高效跟踪周期解随参数 的演化。在Hopf分叉发生后,发现多个周期解分支。选取
的演化。在Hopf分叉发生后,发现多个周期解分支。选取 图1给出了三类周期解,分别见图1中的(a),(b),(c),它们的周期为
图1给出了三类周期解,分别见图1中的(a),(b),(c),它们的周期为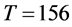 ,
,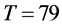 和
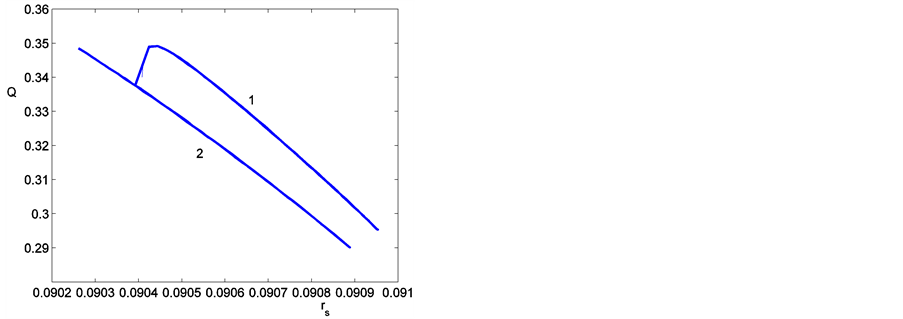
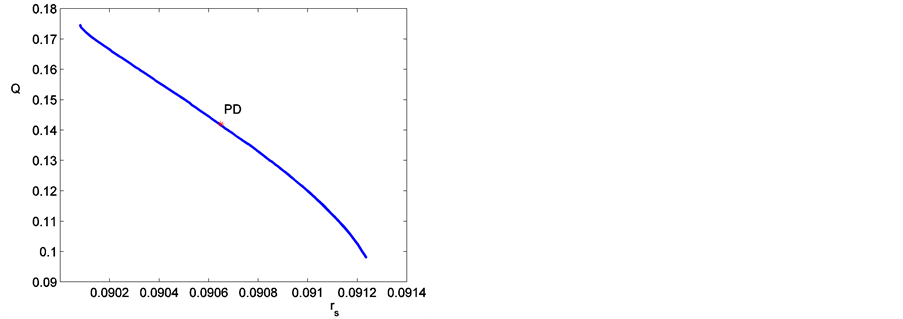
和 。这一点和Haurie实验中所证实的CN振荡的周期在很广泛的一个范围内相吻合。顺着图1所示的三种类型的周期解进行连续延拓,得到了图2中的周期解的连续分支。其中图2(a)的1分支是对应于图1(a)的连续延拓,图2(a)中的2分支是对应于图1(b)的连续延拓,以及图2(b)是对应于图1(c)的连续延拓。
。这一点和Haurie实验中所证实的CN振荡的周期在很广泛的一个范围内相吻合。顺着图1所示的三种类型的周期解进行连续延拓,得到了图2中的周期解的连续分支。其中图2(a)的1分支是对应于图1(a)的连续延拓,图2(a)中的2分支是对应于图1(b)的连续延拓,以及图2(b)是对应于图1(c)的连续延拓。
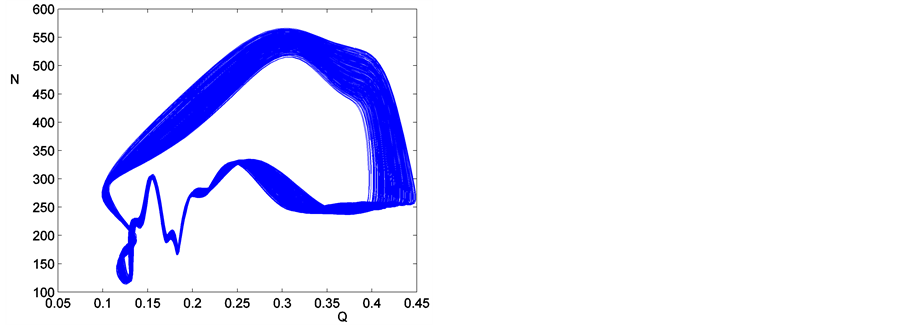
图2(a)中1分支参数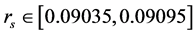 ,将解在Q-N相空间内表示,得到分支1的全部周期吸引子如图3(a)所示,图2(a)中2分支参数
,将解在Q-N相空间内表示,得到分支1的全部周期吸引子如图3(a)所示,图2(a)中2分支参数 ,其在相空间内的全部周期吸引子如图3(b)所示。对于某一
,其在相空间内的全部周期吸引子如图3(b)所示。对于某一 ,周期吸引子要实现从分支2到分支1的转迁,必须遍历多个吸引态。采用相空间压缩法,并施以适当的反馈控制,可以将解限制在分支2的吸引态上。
,周期吸引子要实现从分支2到分支1的转迁,必须遍历多个吸引态。采用相空间压缩法,并施以适当的反馈控制,可以将解限制在分支2的吸引态上。
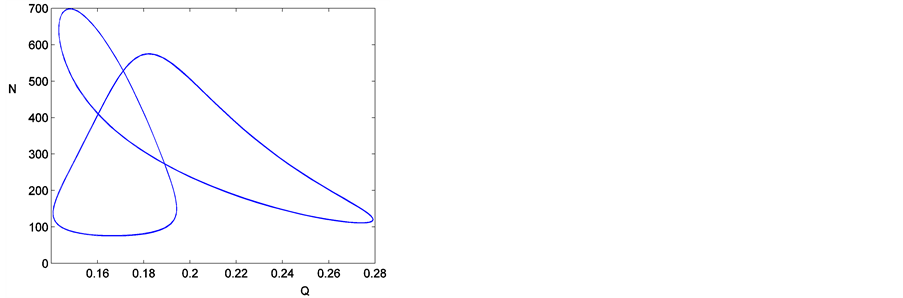
让参数 连续变化,图2(b)中PD表示周期解的倍周期分叉点。周期解分支上稳定周期解的演化可以在相空间表示。具体地,选取
连续变化,图2(b)中PD表示周期解的倍周期分叉点。周期解分支上稳定周期解的演化可以在相空间表示。具体地,选取 得到周期-2解,周期
得到周期-2解,周期 见图4(a),让参数
见图4(a),让参数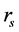 减小到
减小到 ,周期-2解的相图见图4(b),周期
,周期-2解的相图见图4(b),周期 ,进一步减小参数
,进一步减小参数 ,取参数
,取参数 和
和 ,分别得到倍周期解,见图4(c)的周期-4解,周期
,分别得到倍周期解,见图4(c)的周期-4解,周期 ,和(d)的周期-8解
,和(d)的周期-8解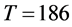 。倍周期分叉是通往混沌的一种路径。进一步减小参数
。倍周期分叉是通往混沌的一种路径。进一步减小参数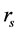 ,在
,在 附近,发现了混沌。
附近,发现了混沌。
3.2. 反馈控制系统
混沌控制问题的研究已经被广泛关注,设计Pyragas延时控制回路,得到如下的反馈控制系统
 (2)
(2)


 (a) Periodic solutions of type I(b) periodic solutions of tyoe II (c) periodic solutions of type III(a) I型周期解 (b) II型周期解 (c) III型周期解
(a) Periodic solutions of type I(b) periodic solutions of tyoe II (c) periodic solutions of type III(a) I型周期解 (b) II型周期解 (c) III型周期解
Figure 1. Three types of different periodic solutions of system (1), 
图1. 系统(1)的三类长周期解,
 (a) (b)
(a) (b)
Figure 2. Continuation extending of periodic solutions with varying parameter . (a) Two branches of continuation periodic solutions respectively obtained by extending periodic solution of type I and type II; (b) One branch of periodic solutions obtained by continuation extending of type III solution
. (a) Two branches of continuation periodic solutions respectively obtained by extending periodic solution of type I and type II; (b) One branch of periodic solutions obtained by continuation extending of type III solution
图2. 周期解随参数 的连续延拓。(a) I型周期解连续延拓得到周期解分支1;II型周期解连续延拓得到周期解分支2;(b) III型周期解分支连续延拓所得周期解分支
的连续延拓。(a) I型周期解连续延拓得到周期解分支1;II型周期解连续延拓得到周期解分支2;(b) III型周期解分支连续延拓所得周期解分支

 (a) (b)
(a) (b)
Figure 3. The whole solutions of continuation of two types of periodic solution, respectively, manifested by (a) periodic solution branch 1; (b) periodic solution 2
图3. 两种类型的吸引子。(a) 周期解分支1的全部吸引子;(b) 周期解分支2的全部吸引子

 (a) (b)
(a) (b)
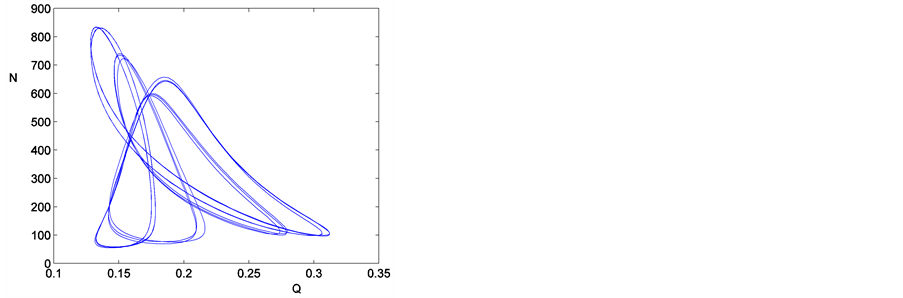 (c) (d)
(c) (d)
Figure 4. Phase portraits of stable periodic solutions of continuation branch of system (1) by varying parameter . (a)
. (a) ; (b)
; (b) ; (c)
; (c) ; (d)
; (d) 
图4. 变化参数 得到稳定解的连续分支上系统(1)周期解的相图。(a)
得到稳定解的连续分支上系统(1)周期解的相图。(a) ;(b)
;(b) ;(c)
;(c)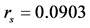 ;(d)
;(d) 
选取不同的 ,可以把混沌控制在不同的周期轨道上。由Poincare截面知,选取不同负反馈增益,将混沌控制在稳定的周期解,周期-2解,周期-4解等,其相图如图5中的(a)和(b)所示。因此实现了将系统稳定嵌入到期望的周期吸引轨上的目的。
,可以把混沌控制在不同的周期轨道上。由Poincare截面知,选取不同负反馈增益,将混沌控制在稳定的周期解,周期-2解,周期-4解等,其相图如图5中的(a)和(b)所示。因此实现了将系统稳定嵌入到期望的周期吸引轨上的目的。
在Pyragas的延时反馈控制方法中增加相控制器,采用相空间压缩法,
 (3)
(3)
 ,选取
,选取 ,从同一初始函数开始,得到解支2上的周期吸引子,其控制效果见图6,但在
,从同一初始函数开始,得到解支2上的周期吸引子,其控制效果见图6,但在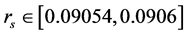 这一小范围内产生了如图6(a)所示的混沌解。图6(b)为
这一小范围内产生了如图6(a)所示的混沌解。图6(b)为 时的吸引子解。进一步采用相空间压缩法,让
时的吸引子解。进一步采用相空间压缩法,让
 (4)
(4)
则可以将系统完全稳定到期望的轨道上,见图6(c),选取 ,得到图6(d)所示的吸引子解。
,得到图6(d)所示的吸引子解。

 (a) (b)
(a) (b)
Figure 5. Chaotic control to stable periodic orbits due to negative feedback control. (a) Chaos with ; (b) Poincare section of chaotic control
; (b) Poincare section of chaotic control
图5. 负反馈增益将混沌控制在稳定的周期轨道。(a)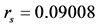 时得到的混沌解;(b) 混沌控制后得到的Poincare截面
时得到的混沌解;(b) 混沌控制后得到的Poincare截面

 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
Figure 6. Phase space contraction to expected stable periodic orbits. (a) Poincare section obtained by controlling method which formulated by (3); (b) Phase portrait onto Poincare section (a) by choosing ; (c) Poincare section obtained by controlling method which formulated by (3) and (4); (b) Phase portrait onto Poincare section (b) by choosing
; (c) Poincare section obtained by controlling method which formulated by (3) and (4); (b) Phase portrait onto Poincare section (b) by choosing 
图6. 相空间压缩法将系统稳定在期望的周期轨道上。(a) 由(3)得到的Poincare截面上的控制效果;(b) 相应于截面(a), 时的相图;(c) 由(3) (4)得到的Poincare截面上的控制效果;(d) 相应于截面(c)
时的相图;(c) 由(3) (4)得到的Poincare截面上的控制效果;(d) 相应于截面(c) 时的相图
时的相图
4. 结论
造血系统中存在很丰富的周期动力学现象。在实验中,Harrie等人发现了嗜中性粒子的振荡周期可以分布在一个很广泛的范围内。本文研究了三类共存的长周期的周期解的连续分支,发现倍周期分叉是通往混沌的路径之一。利用Pyragas的延时反馈控制方法,负反馈增益可将系统稳定嵌入到倍周期分叉的不同周期轨道上。在Pyragas的延时反馈控制方法中增加相控制器,正反馈增益可将系统稳定到期望的吸引态。
文章引用
马苏奇. 造血系统中的周期解分岔及反馈控制
Bifurcation of Periodic Solution of a Hematopological System and Feedback Control[J]. 应用数学进展, 2016, 05(03): 487-493. http://dx.doi.org/10.12677/AAM.2016.53059
参考文献 (References)
- 1. Apostu, R. and Mackey, M.C. (2008) Understanding Cyclical Thrombocytopenia: A Mathematical Modeling Approach. Journal of Theoretical Biology, 251, 297-316. http://dx.doi.org/10.1016/j.jtbi.2007.11.029
- 2. Bernard, S., Bélair, J. and Mackey, M.C. (2003) Oscillations in Cyclical Neutropenia: New Evidence Based on Mathematical Modeling. Journal of Theoretical Biology, 223, 283-298. http://dx.doi.org/10.1016/S0022-5193(03)00090-0
- 3. Haurie, C., Dale, D.C. and Mackey, M.C. (1999) Occurrence of Periodic Oscillations in the Differential Blood Counts of Congenital, Idiopathic, and Cyclical Neutropenic Patient before and during Treatment with G-CSF. Experimental Hematology, 27, 401-409. http://dx.doi.org/10.1016/S0301-472X(98)00061-7
- 4. Haurie, C., Person, R., Dale, D.C. and Mackey, M.C. (1999) Hematopoietic Dynamics in Grey Collies. Experimental Hematology, 27, 1139-1148. http://dx.doi.org/10.1016/S0301-472X(99)00051-X
- 5. Zhuge, C.J., Lei, J. and Mackey, M.C. (2012) Neutrophil Dynamics in Response to Chemotherapy and G-CSF. Journal of Theoretical Biology, 293, 111-120. http://dx.doi.org/10.1016/j.jtbi.2011.10.017
- 6. Lei, J. and Mackey, M.C. (2011) Multistability in an Age-Structured Model of He-matopoiesis: Cyclical Neutropenia. Journal of Theoretical Biology, 270, 143-153. http://dx.doi.org/10.1016/j.jtbi.2010.11.024