Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19096,9
pages
10.12677/AAM.2016.54085
Capacity Study of Urban Road Based on Birth and Death Processes
Yirong Wang, Chengdong Wei*
School of Mathematics and Statistics, Guangxi Teachers Education University, Nanning Guangxi

Received: Nov. 8th, 2016; accepted: Nov. 24th, 2016; published: Nov. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Firstly, the changing process of the road traffic capacity is studied by using the Line Graph and the Fitting analysis. Then, the Q-V-K model is used to quantitatively analyze the difference of the capacity of the road when different lanes are occupied. In addition, the vehicle arrival rate was tested by K-S test, and the results show that it obeys the Poisson distribution. At last, the model of the relationship among vehicle queue length, queuing time and road traffic capacity is established by using the Birth and Death process.
Keywords:Line Graph, Fitting Analysis, Q-V-K Model, K-S Test, Birth and Death Processes

基于生灭过程的城市道路通行能力研究
王一茸,韦程东*
广西师范学院数学与统计科学学院,广西 南宁

收稿日期:2016年11月8日;录用日期:2016年11月24日;发布日期:2016年11月29日

摘 要
首先利用折线图和拟合分析,研究了车道被占用时道路通行能力的变化过程,接着利用交通流模型定量地分析了不同车道被占用道路通行能力的差异,然后对车辆到达率进行了K-S检验,结果显示符合泊松分布,最后利用生灭过程建立车辆排队长度、排队时间和道路通行能力的关系模型。
关键词 :折线图,拟合分析,交通流模型,K-S检验,生灭过程模型

1. 问题背景
如今,交通越来越发达,车辆数量激增,导致交通事故频繁发生,车道被占用的情况随之增加。特别是城市道路,其交通流密度大、连续性强,一条车道被占用,即使时间短,也可能降低道路的通行能力、引起车辆排队、出现交通拥堵。所以有必要对车道被交通事故占用后的道路通行能力和车辆排队长度进行研究。
2. 国内外研究现状
道路通行能力的研究起始于美国。美国出版的《道路通行能力手册》(简称HCM)问世以来,不断更新换代,对美国道路通行能力的计算方法不断完善。继美国之后,英、法、德、日等许多国家也相继出版了符合各自国情的HCM,对道路通行能力的研究不断深入。90年代,国外许多国家对信号交叉口、非信号交叉口、环形交叉口、自行车道等的通行能力从理论上进行研究与改进,并召开了多次通行能力的国际研讨会,对道路通行能力的计算方法不断改进与提高。虽然国外已经将通行能力运用于某些交通理论中,但由于问题所涉及的的交通现象复杂、分析方法不同和尚未建立起一套公认的理论体系等原因,导致鲜有较为突出、具有普遍意义的理论成果 [1] 。
在国内,随着改革开放,汽车和公路的数量都在急剧增长,我国开始逐渐学习引进国外的研究方法,并结合国情开展了大量关于通行能力的课题研究。其中东南大学曾就环形交叉口的通行能力、信号交叉口的通行能力、混合交通路段及无信号交叉口通行能力的影响等进行了较深入的研究,并分析了交通特性等,取得了一定的研究成果。随着经济的增长,迫切需要增加道路的数量,提高道路的质量,这对通行能力的研究提出了更高的要求,有必要建立适合我国道路和交通条件的理论模型 [2] 。
在实际交通系统中,道路的通行能力受到许多不确定因素的影响,如交通事故、恶劣天气、道路维护等。正是由于这些不确定性因素的存在,导致道路经常发生不可预测的交通拥堵,为了更好地对交通行为进行定量化的描述,完善道路通行能力的研究,有必要针对性地研究诸多随机因素影响下的道路实际通行能力。本文主要基于发生交通事故时车道被占用对城市道路通行能力影响的研究。
3. 数据获取及数据采集
数据来源于2013年全国大学生数学建模竞赛A题 [3] 。根据所给的两个视频,我们采集数据的方法为:1) 按车道采集:分为车道一、车道二和车道三。2) 按车辆大小采集:分为大型车和中小型车。3)按周期采集:分为事故发生前、事故发生时、事故解除后,其中每一分钟进行一次车辆计数。在解答问题之前我们把各车型都转换为标准车型,不同车辆类型的折算系数如表1所示,并对所采集来的数据进行了包括筛选、统计、调整和计算等一系列的数据处理过程。
4. 模型的假设
1) 假设在视野范围内所数的车辆数是实际的车辆数;2) 假设除肇事司机外都遵守交通法规;3) 假
Table 1. Conversion coefficients of various vehicle types [4]
表1. 各种车型的折算系数 [4]
设采集到的数据所存在的误差在合理范围之内,且能真实反应该路况信息;4) 假设所有的数据都是可靠的,不包括人为造成的不合理因素;5) 假设视频中的穿过道路的行人对该车道的通行能力无影响;6) 假设只考虑四轮及以上机动车、电瓶车的交通流量,且换算成标准车当量数。
5. 实际通行能力
5.1. 数据处理
道路通行能力 [5] 是指道路上某一点某一车道或某一断面处,单位时间内可能通过的最大交通实体(车辆或行人)数,单位用辆/秒表示。当有其它车辆混入时,均采用等效通行能力的当量标准车辆为单位(pcu)。为了方便数据统计处理,这里的实际通行能力近似于该路段在饱和情况下的单位时间内的交通量,且是按照1分钟的标准车当量数计量的。图1为视频1和视频2中交通事故简易图,表2和表3分别为视频1和视频2的数据统计及处理。
5.2. 实际通行能力变化过程分析
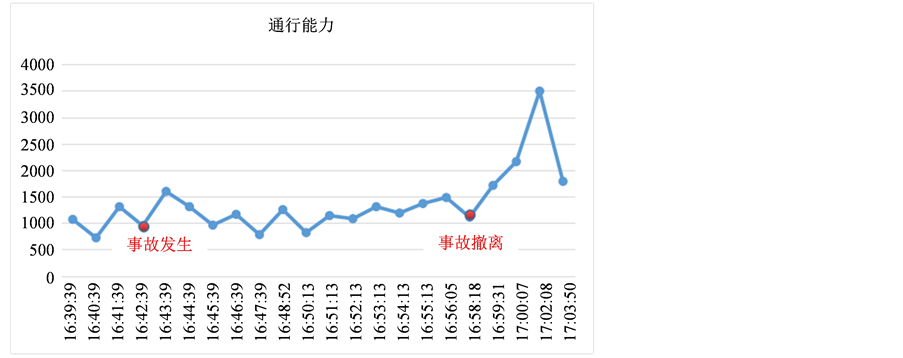
我们在事故发生前至事故结束后这段时间内,利用Excel对每分钟的道路通行能力的变化做了统计,并用图像将它们的变化关系表示出来,如图2所示。
从图2(a)中可以看出,事故发生时至事故撤离期间,道路通行能力都处于低下而上下波动、但波动不大的状态。在事故撤离之后通行能力急剧上升,道路恢复正常通车。从图2(b)中可以看出,事故刚发生时,道路的通行能力处于较平稳的状态,事故发生了十分钟左右,通行能力开始突然回升,这是由于上游路口转为绿灯使车辆增多导致的,但好景不长,两分钟左右之后,又回到初始的较稳定的低下通行能力状态,直至事故撤离,道路通行能力才开始急剧上升,恢复正常通车。
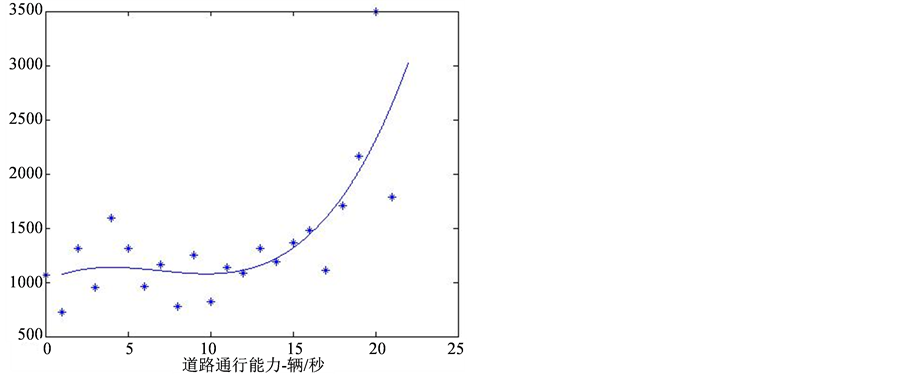
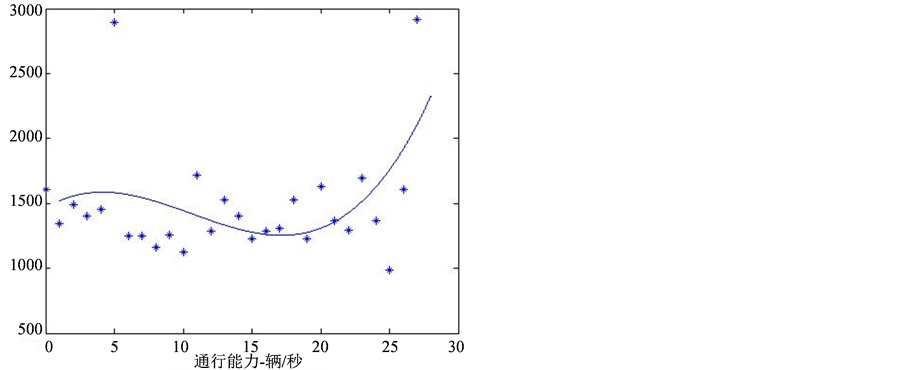
由于视频中有多处出现片段的中断,影响计数,因此需要剔除数据异常点,或者对数据进行平滑性处理。所以接下来我们剔除了异常数据,利用MATLAB软件对数据进行拟合,经过对比发现3次拟合相似度比较高。最后得到视频1的拟合方程为: ,拟合图像为图3(a);视频2的拟合方程为:
,拟合图像为图3(a);视频2的拟合方程为: ,拟合图像为图3(b)。
,拟合图像为图3(b)。
由图3可以观测到事故发生后视频1的车流量缓慢降低,约12分钟后通行能力又逐步上升,视频2的车流量迅速降低,约20分钟后通行能力逐步回升,事故解除后通行能力均达到最大值。
5.3. 不同车道被占用道路通行能力的差异分析
由图1可知,视频1交通事故发生在车道1和车道2,而视频2发生在车道2和车道3,我们可以看到交通事故所占车道不同对道路通行能力影响是有差异的,这可能是由于事故发生的时间点不一样造成的,一个是临近下班高峰期,一个刚好是下班高峰期,还可能是因为每条车道的车流量不一样而造成的。那么哪个车道被占用对道路通行能力的影响更大呢?这需要我们进行定量分析来说明。
Table 2. Statistics and processing of data in the first video
表2. 视频1数据的统计及处理
Table 3. Statistics and processing of data in the second video
表3. 视频2数据的统计及处理
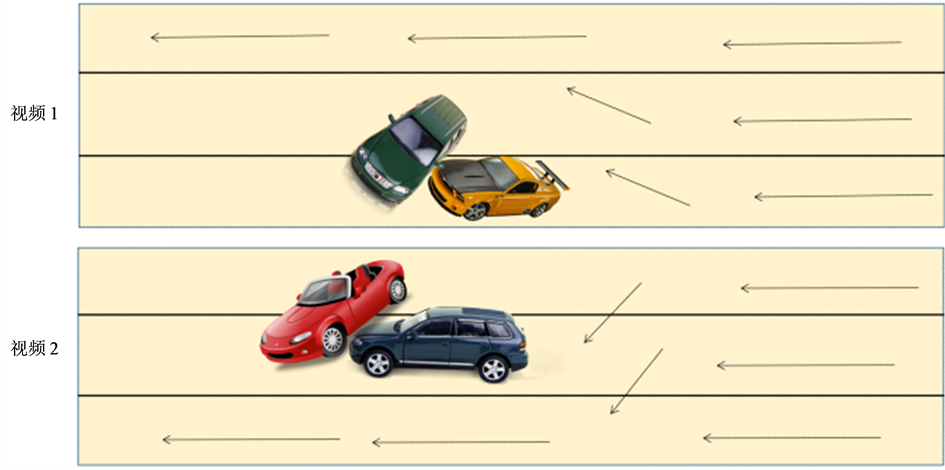
Figure 1. Simple figure about the traffic accident in the first and second video
图1. 视频1和视频2中交通事故发生简易图
 (a)
(a) (b)
(b)
Figure 2. The changing process of the first and second video traffic capacity
图2. 视频1和视频2中事故所处横截面的道路实际通行能力变化过程
 (a) (b)
(a) (b)
Figure 3. The fitting of changing of the road traffic capacity in the first and second video
图3. 视频1和视频2的道路通行能力变化拟合图
由交通流理论 [6] 可知,交通流不是恒定不变的,而是随时间、空间而变化,交通流量、车速、和交通密度三变量之间的相互关系的描述,可表示为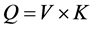 。其中,
。其中,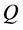 表示交通流量(pcu/h),
表示交通流量(pcu/h), 表示路段行车速度(km/h),
表示路段行车速度(km/h), 表示平均车流密度(pcu/km)。
表示平均车流密度(pcu/km)。
针对视频1,从16:42至16:55这13分钟中,连续地随机测算出车辆的平均车速为 ,交通流量
,交通流量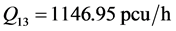 ,平均车流密度
,平均车流密度 。
。
针对视频2,从17:34至18:02这28分钟里,连续随机测算出车辆的平均车速为 ,交通流量
,交通流量 ,平均车流密度
,平均车流密度 。
。
通过定量分析可以发现,视频1的事故发生点到事故撤离时间段内的平均通行能力为1146.95 pcu/h,视频2的事故发生点到事故撤离时间段内的平均通行能力为1443 pcu/h。因此,视频2的单位时间内通过的车较多,即视频2的平均通行能力大于视频1的平均通行能力。可见,车道一二被占用比车道二三被占用的对道路通行能力的影响更大。
6. 基于生灭过程的车辆排队模型
6.1. Kolmogorov-Smirnov检验
Kolmogorov-Smirnov检验(柯尔莫哥洛夫-斯摩洛夫)被称作拟合优度检验法,简称K-S检验。它是一个用来检验模拟所得数据的分布是否符合一个理论的已知分布的方法,它的基本原理是以样本数据的累计频率分布与特定理论分布进行比较,若两者的差距很小,则推断该样本取自某特定分布族。本节基于MATLAB软件实现来检验样本数据的总体分布是否服从泊松分布,其检验步骤及过程如下:
1) 条件设定。H0:样本数据的总体分布不服从泊松分布;H1:样本数据的总体分布服从泊松分布。
2) 检验准备。对于H1,已经假定样本数据服从泊松分布,但其强度未知,利用poissfit(x,alpha)函数估算出模拟泊松过程的强度,再利用poisscdf(x,lamda)函数得到泊松分布的累积分布函数。
3) K-S检验。直接调用K-S检验函数kstest(x,[x,p],alpha),其中,x为输入的样本数据,P为累积分布函数,1- alpha为置信区间,当结果 时,则输入数据满足泊松分布,否则,不满足泊松分布。
时,则输入数据满足泊松分布,否则,不满足泊松分布。
根据MATLAB输出结果可知,视频1和视频2的样本数据均服从泊松分布(见程序3和4)。
6.2. 基于生灭过程道路通行能力的研究
生灭过程是描述生物系统中生灭现象的一种随机过程,主要研究的是系统内部状态的变化过程,处理的是到达率为泊松分布,时间服从负指数分布的一种数学方法。其定义如下:
设齐次马尔可夫过程 的状态空间为
的状态空间为 ,转移概率为
,转移概率为 ,如果
,如果

则称 为生灭过程,
为生灭过程,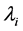 为出生率,
为出生率,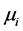 为死亡率 [7] 。
为死亡率 [7] 。
在车辆堵塞排队中,由K-S检验可知车辆的到达率符合泊松分布,所以车辆堵塞排队过程可以利用生灭过程进行处理。根据生灭过程的定义可设该堵车系统有 个状态(车辆数),记系统在时刻
个状态(车辆数),记系统在时刻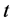 的状态为
的状态为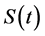 ,则在很短的时间
,则在很短的时间 内,车辆数的变化有三种可能:系统状态由
内,车辆数的变化有三种可能:系统状态由 变到
变到 ,即增加一辆车,其概率为
,即增加一辆车,其概率为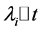 ;系统状态由
;系统状态由 变道
变道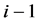 ,即减少一辆车,其概率为
,即减少一辆车,其概率为 ;系统大小不增不减,其概率为
;系统大小不增不减,其概率为 。设系统在时刻
。设系统在时刻 处于状态
处于状态 的概率为
的概率为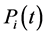 ,即
,即 ,具体转移的概率如下:
,具体转移的概率如下:
1) 由状态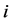 转移到
转移到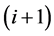 的概率:
的概率:
2) 由状态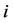 转移到
转移到 的概率:
的概率:
3) 状态保持不变的概率:
上述各式中, 为到达率,
为到达率,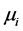 为离开率,
为离开率, ,
,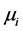 均为正常数,且只与状态
均为正常数,且只与状态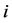 有关。
有关。
设图4为生灭过程的状态转移强度图,可利用柯尔莫哥洛夫方程建立生灭过程的微分方程组。根据该图4可知,系统中每个状态都能够转移到其余任何一个转态,且系统的转态数是有限的,因而有极限概率存在 [8] 。由于极限概率 是常数,常数的微分等于零,所以令柯尔莫哥洛夫方程的等号左边为零,则可把微分方程变成代数方程求解。根据系统平衡的原理列出图4中的状态代数方程,其一般方法如下:方程等号左边为给定的状态概率
是常数,常数的微分等于零,所以令柯尔莫哥洛夫方程的等号左边为零,则可把微分方程变成代数方程求解。根据系统平衡的原理列出图4中的状态代数方程,其一般方法如下:方程等号左边为给定的状态概率 乘上从给定状态发出的流的强度
乘上从给定状态发出的流的强度 之和;方程等号右边为所有进入给定状态的概率
之和;方程等号右边为所有进入给定状态的概率 乘上进入给定状态的流的强度
乘上进入给定状态的流的强度 之和 [6] 。为了方便,
之和 [6] 。为了方便, 写成
写成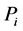 。
。
对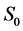 有:
有:
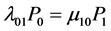 (5.1)
(5.1)
对 有:
有:
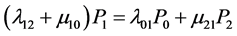 (5.2)
(5.2)
把(5.1)代入(5.2)得:
 ,即
,即 (5.3)
(5.3)
同理,对 有:
有:
 (5.4)
(5.4)
对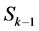 有:
有:
 (5.5)
(5.5)
则极限概率满足下列方程组:
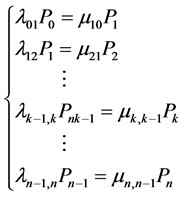 (5.6)
(5.6)

Figure 4. State transition intensity of birth and death processes
图4. 生灭过程的状态转移强度图
且有正则条件
 。 (5.7)
。 (5.7)
解方程组(5.6)的第一个方程得:
 (5.8)
(5.8)
把(5.8)带入方程组(5.6)的第二个方程得:
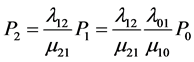 (5.9)
(5.9)
依此类推,求得通式为:

由此可见,所有的状态下的概率都可以通过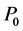 求得,通过正则条件可得:
求得,通过正则条件可得:

则

于是得到任意塞车时刻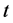 时,在排队的车辆的数量为
时,在排队的车辆的数量为 的概率为:
的概率为:
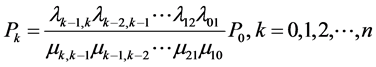
所以车辆排队的平均队长(辆)为:

由此可知,事故发生时,若下游路口车辆的离去是均匀的,当上游路口的车流量增加时,车辆排队的长度也势必增加,排队时间增大,排队长度也会增大;事故解除后,若上游路口车流量趋于稳定,则下游路口车辆的离去率增大,车辆的排队长度随之减少,随着时间的增大,排队长度趋于零,道路恢复正常通车。
7. 总结
文章通过综合使用折线图、拟合分析、交通流、K-S检验和生灭过程等方法,分析了道路通行能力的变化过程,建立了车辆排队长度预测模型,为测量道路通行能力和判断是否出现排队现象提供理论依据。
基金项目
国家自然科学基金项目(11561010);数据科学广西高等学校重点实验室资助项目;大学生创新项目(201410603029)。
文章引用
王一茸,韦程东. 基于生灭过程的城市道路通行能力研究
Capacity Study of Urban Road Based on Birth and Death Processes[J]. 应用数学进展, 2016, 05(04): 738-746. http://dx.doi.org/10.12677/AAM.2016.54085
参考文献 (References)
- 1. 倪艳明. 城市道路交通通行能力影响因素分析及研究[D]: [硕士学位论文]. 广州: 华南理工大学, 2012.
- 2. 贾晓敏. 城市道路通行能力影响因素研究[D]: [硕士学位论文]. 西安: 长安大学, 2009.
- 3. 中国工业与应用数学学会. 2013年高教社杯全国大学生数学建模竞赛A题[Z]. 2013.
- 4. 景鹏, 孟祥海. 城市道路车辆分类及折算系数研究[J]. 城市交通, 2006, 4(2): 61-63.
- 5. 李冬梅, 李文权. 道路通行能力的计算方法[J]. 河南大学学报(自然科学版), 2002, 32(2): 24-27.
- 6. 茹红蕾. 城市道路通行能力的影响因素研究[D]: [硕士学位论文]. 上海: 同济大学, 2008.
- 7. 刘次华. 随机过程[M]. 武汉: 华中科技大学出版社, 2011.
- 8. 陆凤山. 排队论及其应用[M]. 长沙: 湖南科学技术出版社, 1984.
NOTES
*通讯作者。
