Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23172,14
pages
10.12677/AAM.2017.69144
Numerical Simulations on Ground States for Rotating Two-Component Bose-Einstein Condensates
Ronghua Liu, Yundan Deng, Chunping Pang, Hanquan Wang
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Dec. 2nd, 2017; accepted: Dec. 19th, 2017; published: Dec. 26th, 2017

ABSTRACT
The ground states of rotating two-component Bose-Einstein condensates (BEC) at extremely low temperature are solutions of time-independent coupled Gross-Pitaevskii equations. To compute the ground states, we propose an efficient numerical method—gradient flows with discrete normalization. In linear cases and under properly chosen initial data, we can prove that the gradient flows converge into the ground state which has the lowest energy. We show that the method is quite efficient and apply the method to study complicated vortex structure in the ground state solutions of rotating two-component BEC at extremely low temperature.
Keywords:Coupled Gross-Pitaevskii Equations, Rotating Two-Component Bose-Einstein Condensates, Gradient Flows
旋转的双原子–玻色爱因斯坦凝聚体基态 数值模拟
刘荣华,邓云丹,庞春平,王汉权
云南财经大学统计与数学学院,云南 昆明
收稿日期:2017年12月2日;录用日期:2017年12月19日;发布日期:2017年12月26日

摘 要
静态相耦合的Gross-Pitaevskii方程组的解描述了双原子的玻色爱因斯坦凝聚体在极低温度下的基态现象。我们提出一种十分有效的数值方法——梯度法来求解此基态解。我们提出的梯度法在数值上既保持总模量守恒又能使总能量递减;我们严格地证明我们提出的梯度法是一种获得能量函数在给定限制性条件下的最小值(也即基态解)的十分有效的方法。我们通过大量的例子来显示该方法的优点并且应用该方法去研究处于旋转状态下的双原子–玻色爱因斯坦凝聚体在极低温度下所呈现的复杂涡旋现象。
关键词 :耦合的Gross-Pitaevskii方程组,旋转状态下的双原子–玻色爱因斯坦凝聚体,梯度法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自从在双原子–玻色爱因斯坦凝聚体的实验中发现涡旋现象后 [1] - [6] ,人们就对旋转状态下的双原子–玻色爱因斯坦凝聚体所具有的一种新的现象——涡旋现象产生了浓厚的兴趣。根据平均场近似理论,静态且相耦合的Gross-Pitaevskii (GP)方程组被用来描述旋转中的双原子–玻色爱因斯坦凝聚体的基态现象 [7] [8] [9] [10] [11] 。事实上,许多关于无旋转的双原子–玻色爱因斯坦凝聚体的基态现象 [12] [13] [14] [15] ,如自然对称现象的破裂 [16] 、中心对称的涡旋 [17] [18] [19] [20] 以及稳定的skyrmions [21] 等揭示了许多实验现象,并解释了许多实验难以解决的问题。
最近我们在文 [22] 中研究了旋转中的双原子–玻色爱因斯坦凝聚体的基态现象,但是我们并没有考虑由外部力场引起的Josephson耦合力。在Josephson耦合力作用下的双原子–玻色爱因斯坦凝聚体的基态现象会不同于没有Josephson耦合力作用的双原子–玻色爱因斯坦凝聚体的基态现象。对于这一问题,就我们所知,只有较少人研究过。我们撰写本文的主要目的是研究在Josephson耦合力作用下的双原子–玻色爱因斯坦凝聚体的基态现象。该基态现象可以用静态且相耦合的GP方程组来描述。为此,我们首先提出一种十分有效的数值方法——梯度法来求解耦合的静态GP方程组。我们提出的梯度法在数值上既保持总模量守恒又能使总能量递减,从而保证用该方法求得能量函数在给定限制性条件下的最小值。我们严格地证明我们提出的梯度法是一种获得能量函数在给定限制性条件下的最小值的十分有效的方法。
本篇论文是按照如下方式组织的。在第二节中我们将介绍用来描述双原子–玻色爱因斯坦凝聚体的相耦合的GP方程组、如何把它们化为无量纲形式的方程组以及如何把三维方程组简化为二维方程组。在第三节中我们详细地讨论如何用梯度法求得相耦合的GP方程组的数值解,我们给出详细的算法并在数学上严格地证明我们提出的方法的有效性。在第四节中我们利用提出的数值方法研究旋转中的双原子–玻色爱因斯坦凝聚体在极低温度下所呈现的涡旋现象。在最后一节,也就是第五节,我们将探讨得到我们的结论以及我们提出的新方法可能用到的领域。
2. 动态相耦合的GP方程组
我们考虑处于旋转状态下的双原子–玻色爱因斯坦凝聚体(比如铷87原子及其同位素)。用来描述该双原子–玻色爱因斯坦凝聚体的数学模型便是以下相耦合的GP方程组 [23]
(2.1)
(2.2)
这里 是描述双原子–玻色爱因斯坦凝聚体的两个玻动函数。 是87Rb原子的质量,调和磁势井函数 用
来表示。 是 轴在上磁势井的中心。角动量转动项为 。双原子内部以及双原子之间的键力分别用 和 来表示。方程组(2.1) (2.2)中的最后一项表示由外部力场引起的Josephson耦合力,并且这里的 是Rabi频率。该相耦合的GP方程组(2.1)~(2.2)保持系统的全部粒子数
(2.3)
不变。这里 是双原子之一的粒子数, 是玻色爱因斯坦双原子总粒子数。该相耦合的GP方程组(2.1)~(2.2)也保持系统的能量
不变。
2.1. 无量纲形式的GP方程组
GP方程组(2.1)~(2.2)不大方便直接用于数值模拟。如果我们引入:
, , , , ,
和 ( )。 (2.4)
事实上这里我们取 和 分别作为时间及长度的无量纲单位。把参数(2.4)代入方程组(2.1)~(2.2)中,并且在方程组(2.1)~(2.2)的两边都乘以 。如果我们再去掉所有的~,则我们可以得到以下的三维的无量纲形式的GP方程组:
(2.5)
并且
,当 ; 当 ,
,
, , (2.6)
。
系统每个粒子的能量成为
(2.7)
这里
2.2. 二维的方程组
方程组(2.5)也可近似地变为二维形式的方程组。在磁势井是圆盘形式时,我们可假设 ,这里的 。将之代入方程组(2.5),我们可把偶合的GP方程组(2.5)转化成一个二维的无量纲形式的GP方程组。
这里 ,当 ; ,当 。 。
总之,我们将讨论以下无量纲形式且相耦合的GP方程组,
(2.9)
这里 或者3, , 。
2.3. GP方程组(2.9)的一些性质
为方便起见,本节我们将讨论GP方程组(2.9)的一些解析性质。
当 时,(2.9)式中两个重要的守恒量。一个是总模量
(2.10)
守恒;另一个是总能量
(2.11)
守恒,这里
,
。
3. 静态相耦合的GP方程组
为了寻求(2.9)式的一种静态解(它们通常被用来描述旋转中的双原子–玻色爱因斯坦凝聚体的平衡态现象),为此,我们引入
(3.1)
这里 是这两种粒子之间的化学势能, 是与时间无关的函数。函数 被用来描述旋转中的双原子–玻色爱因斯坦凝聚体的平衡态现象。
将(3.1)带入(2.9)式得到以下只与 有关且与时间无关的GP方程组
(3.2)
(3.3)
当对这两部分进行标准化时,我们需要总模量
(3.4)
我们知道化学势能
(3.5)
并且,双原子–玻色爱因斯坦凝聚体的能量可以表示为:
(3.6)
函数 所满足的静态相耦合的GP方程组(3.2)~(3.4)实际是一个带有约束条件的非线性特征函数与特征值问题。静态相耦合的GP方程组(3.2)~(3.4)有许多解,
人们最关心的是下面的基态解。
3.1. 基态解的定义
旋转中的双原子玻色爱因斯坦凝聚体的基态解 实际上是能量函数 在限制条件(3.4)下的取得最小值时对应的函数,也就是
(A)找到 使得
,
,
这里的 定义为:
。
我们可以证明 满足:
且 。
很明显,静态相耦合的GP方程组(3.2)~(3.4)有许多解,基态解只是其中一类我们最关心的解。在物理学上,通常把GP方程组(3.2)~(3.4)除基态解以外的其它解称为激发态解,这是因为这些解所对应的能量比基态解所对应的能量 高。
3.2. 求基态解的数值方法
我们首先构建连续的梯度流
(3.7)
(3.8)
(3.9)
(3.10)
这里
(3.11)
并且 是 中的一个有界区域。 。
对于连续的梯度流(3.7)~(3.10),我们有下面的定理,
定理3.1:在临界条件(3.9)和初始条件(3.10)下,连续的梯度流(3.7)~(3.8)满足
(1) (3.12)
(2) (3.13)
这个定理的证明虽然很长但证法很简单,这里我们将省略,不再陈述。
从定理3.1我们可以知道连续的梯度流(3.7)~(3.10)可保持总模量守恒和能量递减的性质。并且,当 时,我们可得到 和 接近于稳定状态时的解,这时的能量函数 在U空间上处于能量最低的状态。如果我们能为方程(3.9)引入一个合适的初始条件 ,就可以找到方程组(3.7)~(3.10)的稳态解,也就找到了问题(A)的基态解:
。
其次,从时间 到 ,我们希望求得方程组(3.7)~(3.10)的数值解,为了避免每步计算化学势能,我们取而代之考虑下面的离散梯度流:
(3.14)
(3.15)
(3.16)
(3.17)
(3.18)
从离散梯度流(3.14)~(3.16),我们发现他们在能量减少时的某种条件下的性质。
我们令
(3.19)
代入到梯度流(3.14)~(3.16),很容易建立以下基本事实:
引理3.1:假设 ,且 ,那么
(i) 对于所有的 和 有 ,我们有:
。
(ii) 如果 ,那么
(3.20)
证明:
(i)
这就证明了(i)中的结果。
(ii) 这个证明可以仿照 [24] 中的相关证明。这里,具体证明省略
从引理3.1,我们可直接得到:
定理3.2:设 ,如果 ,梯度流(3.14)~(3.16)满足
(1) ;
(2)
(3.21)
事实上,方程中的标准化步骤(3.16)等同于准确地求解下面普通的常微分方程组
。 (3.22)
(3.23)
这里 并且
(3.24)
因此,梯度流(3.14)~(3.16)可以看作作为下面离散带有间断系数的梯度流的一种一阶分裂法
(3.25)
(3.26)
对于上面的梯度流(3.25),让 并且注意到 (方程(3.23)的右边)在 时是方程(3.23)的求解,我们得到
(3.27)
这里
(3.28)
在下一小节里,我们给出离散梯度流(3.14)~(3.16)的一种差分格式。
离散梯度流(3.14)~(3.16)的一种差分格式
我们这里仅仅只考虑二维情形,三维情形的差分格式是类似的。假设我们计算的区域为 。我们选择时间步长 以及空间步长 和 。并且 和 (这里M和N均是偶的正整数)。空间上以及时间上的网格点分别为 以及 :
设 表示函数 在点 处的近似值( )。利用有限差分法,我们可得到下面的一种离散梯度流(3.14)~(3.16)的差分格式:
(3.29)
(3.30)
上述方程组(3.29)~(3.30)对所有的 ,都成立。
并且
,
,
,
这里的 的定义为 。
4. 数值实验结果
在本节的数值计算中,我们应用差分格式(3.29)~(3.30)来计算二维情形的基态解。因为当前成功的双原子–玻色爱因斯坦凝聚体实验主要考虑87Rb及它的同位素 [25] 和23Na及它的同位素 [3] ,所以在我们的数值计算中,我们仅仅考虑
。
关于相互作用的参数,我们也仅仅主要考虑下面三种情形
情形I: ,
情形II: ,
情形III: 。
其中情形II与情形III分别对应相应实验中的参数。在情形I中,两种原子内部以及两种原子之间均有相同的相互作用力;在情形II中,两种原子之间有相同的相互作用力,但是两种原子内部没有相同的相互作用力;在情形III中,两种原子之间有相同的相互作用力,但是两种原子内部没有相同的相互作用力。
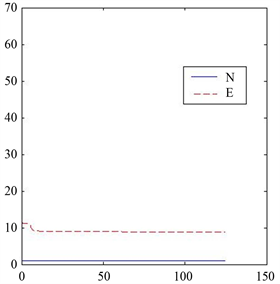
Figure 1. Case I, , , ,
图1. 情形I, , , ,
在图1中,N与E分别代表总模量与能量,它们是总模量(2.10)与能量(2.11)的数值近似。从图1中的结果,我们可以看出:我们的数值方法差分格式(3.29)~(3.30)在数值上能保证总模量守恒,且能量递减。
从图2中的结果,我们可以看出:(1) 在双原子–玻色爱因斯坦凝聚体的基态中,当两原子都含有数量较多的涡旋时且 ,它们分别形成涡旋网格;(2) 在双原子–玻色爱因斯坦凝聚体的基态中,一种原子的涡旋与另一种原子的涡旋镶嵌在一起;(3) 在双原子–玻色爱因斯坦凝聚体的基态中,随着 的增大,两种原子所含的涡旋数量也增大。
从图3中的结果,我们可以看出:(1) 在双原子–玻色爱因斯坦凝聚体的基态中,当两原子都含有数量较多的涡旋时且 ,它们分别形成带状的涡旋;(2) 在双原子–玻色爱因斯坦凝聚体的基态中,一种原子的涡旋与另一种原子的涡旋镶嵌在一起;(3) 在双原子–玻色爱因斯坦凝聚体的基态中,随着 的增大,两种原子所含的涡旋数量也增大。
从图4中的结果,我们可以看出:(1) 在双原子–玻色爱因斯坦凝聚体的基态中,两原子都含有数量较多的涡旋,一种原子的涡旋与另一种原子的涡旋镶嵌在一起;(2) 在双原子–玻色爱因斯坦凝聚体的基态中,随着 的增大,两种原子所含的涡旋数量也增大。
从图5中的结果,我们可以也看出:(1) 在双原子–玻色爱因斯坦凝聚体的基态中,两原子都含有数量较多的涡旋,一种原子的涡旋与另一种原子的涡旋镶嵌在一起。
在图6中,我们有较大的Josephson耦合力作用。从图6中的结果,我们可以也看出:(1) 在双原子–玻色爱因斯坦凝聚体的基态中,两原子都含有数量较多的涡旋;(2) 在双原子–玻色爱因斯坦凝聚体的基态中,一种原子的涡旋不是另一种原子的涡旋镶嵌在一起,而是它们都含有相同数量及同样形态的涡旋;(3) 在双原子–玻色爱因斯坦凝聚体的基态中,随着 的增大,两种原子所含的涡旋数量也增大。

Figure 2. Case I, , ,
图2. 情形I, , ,

Figure 3. Case I, , ,
图3. 情形I, , ,

Figure 4. Case II, ,
图4. 情形II, ,

Figure 5. Case III, ,
图5. 情形III, ,

Figure 6. Case III, ,
图6. 情形III, ,
5. 结论
我们提出了一种梯度法来求解静态相耦合的GP方程组,并且应用该方法去研究旋转中的双原子–玻色爱因斯坦凝聚体在极低温度下所呈现的基态现象。我们提出的梯度法在数值上既保持总模量守恒又能使总能量递减。我们在数学上我们严格地证明我们提出的梯度法是一种获得能量函数在给定限制性条件下的最小值的十分有效的方法。在基态现象中,如果在双原子–玻色爱因斯坦凝聚体添加了Josephson耦合力后,我们发现复杂的涡旋结构。将来我们要做的工作是将我们新提出的梯度法应用到三维情形,因为它更有利于模拟双原子–玻色爱因斯坦凝聚体在极低温度下所呈现的基态现象,特别是涡旋现象的结构。
基金项目
国家自然科学基金项目(91430103)的资助。
文章引用
刘荣华,邓云丹,庞春平,王汉权. 旋转的双原子–玻色爱因斯坦凝聚体基态数值模拟
Numerical Simulations on Ground States for Rotating Two-Component Bose-Einstein Condensates[J]. 应用数学进展, 2017, 06(09): 1187-1200. http://dx.doi.org/10.12677/AAM.2017.69144
参考文献 (References)
- 1. Bao, W. and Du, Q. (2004) Computing the Ground State Solution of Bose-Einstein Condensates by a Normalized Gra-dient Flow. SIAM Journal on Scientific Computing, 25, 1674-1697.
https://doi.org/10.1137/S1064827503422956 - 2. Kasamatsu, K., Tsubota, M. and Ueda, M. (2003) Structure of Vortex Lattices in Rotating Two-Component Bose-Einstein Condensates. Physica B: Condensed Matter, 329-333, 23-24.
https://doi.org/10.1016/S0921-4526(02)01877-X - 3. Miesner, H.J., Stamper-Kurn, D.M., Stenger, J., Inouye, S., Chikkatur, A.P. and Ketterle, W. (1999) Observation of Metastable States in Spinor Bose-Einstein Condensates. Physical Review Letters, 82, 2228
https://doi.org/10.1103/PhysRevLett.82.2228 - 4. Seiringer, R. (2002) Gross-Pitaevskii Theory of the Rotating Bose Gas. Communications in Mathematical Physics, 229, 491-509.
https://doi.org/10.1007/s00220-002-0695-2 - 5. Trippenbach, M., Góral, K., Rzazewski, K., Malomed, B. and Band, Y.B. (2000) Structure of Binary Bose-Einstein Condensates. Journal of Physics B: Atomic, Molecular and Optical Physics, 33, 4017-4031
https://doi.org/10.1088/0953-4075/33/19/314 - 6. Wang, H. (2007) A Time-Splitting Spectral Method for Cou-pled Gross-Pitaevskii Equations with Applications to the Dynamics of Rotating Bose-Einstein Condensates. Journal of Computational and Applied Mathematics, 205, 88-104.
https://doi.org/10.1016/j.cam.2006.04.042 - 7. Castin, Y. and Dum, R. (1999) Bose-Einstein Condensates with Vortices in Rotating Traps. The European Physical Journal D, 7, 399-412.
https://doi.org/10.1007/s100530050584 - 8. García-Ripoll, J.J. and Pérez-García, V.M. (2002) Split Vortices in Optically Coupled Bose-Einstein Condensates. Physical Review A, 66, 021602.
https://doi.org/10.1103/PhysRevA.66.021602 - 9. Kasamatsu, K., Tsubota, M. and Ueda, M. (2003) Vortex Phase Diagram in Rotating Two-Component Bose-Einstein Condensates. Physical Review Letters, 91, 150406.
https://doi.org/10.1103/PhysRevLett.91.150406 - 10. Mueller, E.J. and Ho, T.-L. (2002) Two-Component Bose-Einstein Condensates with a Large Number of Vortices. Physical Review Letters, 88, 180403.
https://doi.org/10.1103/PhysRevLett.88.180403 - 11. Schweikhard, V., Coddington, I., Engels, P., Tung, S. and Cornell, E.A. (2004) Vortex-Lattice Dynamics in Rotating Spinor Bose-Einstein Condensates. Physical Review Letters, 93, 210403.
https://doi.org/10.1103/PhysRevLett.93.210403 - 12. Bao, W. (2004) Ground States and Dynamics of Mul-ti-Component Bose-Einstein Condensates. SIAM Multiscale Modeling & Simulation, 2, 210-236.
https://doi.org/10.1137/030600209 - 13. Chang, S.M., Lin, W.W. and Shieh, S.F. (2005) Gauss-Seidel-Type Methods for Energy States of Multi-Component Bose-Einstein Condensates. Journal of Computational Physics, 202, 367-390.
https://doi.org/10.1016/j.jcp.2004.07.012 - 14. Pu, H. and Bigelow, N.P. (1998) Properties of Two-Species Bose Condensates. Physical Review Letters, 80, 1130.
https://doi.org/10.1103/PhysRevLett.80.1130 - 15. Riboli, F. and Modugno, M. (2002) Topology of the Ground State of Two Interacting Bose-Einstein Condensates. Physical Review A, 65, 063614.
https://doi.org/10.1103/PhysRevA.65.063614 - 16. Esry, B.D. and Greene, C.H. (1999) Spontaneous Spatial Symmetry Breaking in Two-Component Bose-Einstein Condensates. Physical Review A, 59, 1457-1460.
https://doi.org/10.1103/PhysRevA.59.1457 - 17. Chui, S.T., Ryzhov, V.N. and Tareyeva, E.E. (2001) Vortex States in Binary Mixture of Bose-Einstein Condensates. Physical Review A, 63, 023605.
https://doi.org/10.1103/PhysRevA.63.023605 - 18. García-Ripoll, J.J. and Pérez-García, V.M. (2000) Stable and Unstable Vortices in Multicomponent Bose-Einstein Condensates. Physical Review Letters, 81, 4264.
https://doi.org/10.1103/PhysRevLett.84.4264 - 19. Ho, T.L. and Shenoy, V.B. (1996) Binary Mixtures of Bose Condensates of Alkali Atoms. Physical Review Letters, 77, 3276.
https://doi.org/10.1103/PhysRevLett.77.3276 - 20. Vekslerchik, V. and Pérez-García, V.M. (2003) Exact Solution of the Two-Mode Model of Multicomponent Bose- Einstein Condensates. Discrete & Continuous Dynamical Sys-tems—B, 3, 179-192.
https://doi.org/10.3934/dcdsb.2003.3.179 - 21. Battye, R.A., Cooper, N.R. and Sutcliffe, P.M. (2002) Stable Skyrmions in Two-Component Bose-Einstein Condensates. Physical Review Letters, 88, 080401.
https://doi.org/10.1103/PhysRevLett.88.080401 - 22. Wang, H. (2009) Numerical Simulations on Stationary States for Rotating Two-Component Bose-Einstein Condensates. Journal of Scientific Computing, 38, 149-163.
https://doi.org/10.1007/s10915-008-9225-5 - 23. Zhang, Y., Bao, W. and Li, H. (2007) Dynamics of Rotating Two-Component Bose-Einstein Condensates and Its Efficient Computation. Physica D, 234, 49-69.
https://doi.org/10.1016/j.physd.2007.06.026 - 24. Bao, W., Wang, H.Q. and Markowich, P.A. (2005) Ground State, Symmetric and Central Vortex State in Rotating Bose-Einstein Condensate. Communications in Mathematical Sciences, 3, 57-88.
https://doi.org/10.4310/CMS.2005.v3.n1.a5 - 25. Hall, D.S., Matthews, M.R., Ensher, J.R., Wieman, C.E. and Cornell, E.A. (1998) Dynamics of Component Separation in a Binary Mixture of Bose-Einstein Condensates. Physical Review Letters, 81, 1539-1542.
https://doi.org/10.1103/PhysRevLett.81.1539