Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24710,10
pages
10.12677/AAM.2018.74055
Single-Machine Scheduling with Due-Window Assignment and Convex Resource Allocation
Shi Li, Chengxin Luo
School of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning

Received: Apr. 12th, 2018; accepted: Apr. 21st, 2018; published: Apr. 28th, 2018

ABSTRACT
We consider a single machine scheduling problem with learning effect and deterioration effect. The actual processing time of a job is a convex function of the resource amount allocated to it. All jobs have a common due-window. The actual processing time of each job is a convex function dependent on the workload of the job, its starting time and its allocation of non-renewable resource. We consider three models. For the first we aim to minimize the weighted costs of earliness, tardiness, the starting time of the common due-window, the size of the due-window, the makespan and the total completion time. For the second, we constrain the total resource amount to minimize the weighted costs of earliness, tardiness, the starting time of the common due-window, the size of the due-window, the makespan and the total completion time. For the third, we are subject to the constraint that the total cost with early and tardy cost is less than or equal to a fixed amount to minimize the total resource. We show that the problems are polynomial solvable by transforming them into matching problems. Three optimal algorithms are given.
Keywords:Scheduling, Resource Allocation, Deterioration Effect, Learning Effect, Matching Problem, Due-Window
带有工期窗口和凸资源分配的 单机排序问题
李 石,罗成新
沈阳师范大学数学与系统科学学院,辽宁 沈阳

收稿日期:2018年4月12日;录用日期:2018年4月21日;发布日期:2018年4月28日

摘 要
讨论具有学习效应和退化效应且工件的加工时间依赖于资源分配的单机排序问题。在凸资源消费函数条件下研究目标函数,所有工件有一个公共工期窗口,工件的实际加工时间依赖于分配给工件的任务量以及不可再生资源数量,同时依赖于工件的开始加工时间,分别考虑了三种情况,第一种是使带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和最小的问题;第二种是资源费用受限的情况下,极小化带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和问题。第三种是在带有提前,延误等总费用受限的情况下,极小化总资源量。将上述三种问题转化为匹配问题,并证明其是多项式时间可解的,分别给出三个最优算法。
关键词 :排序,资源分配,退化效应,学习效应,匹配问题,工期窗口

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在经典排序问题中一个公认的假设是工件的加工时间不受其他因素影响,即为一个恒定的常值,但在实际生产过程中,会经常遇到工件的实际加工时间可变的情况。影响工件的实际加工时间因素多种多样,如因机器老化而造成的退化效应或因工人反复操作提高技术而产生的学习效应,或资源分配等情况。Biskup [1] ,Gawiejnowicz [2] ,Shabtay [3] 分别研究了工件加工时间变化的问题。Wang and Wang [4] [5] 研究了工件的加工时间依赖于退化效应和资源分配的情况。Wang,Wang and Ji [6] 研究了单机排序问
题,且工件 的实际加工时间的表达式为
的实际加工时间的表达式为 其中
其中 表示工件
表示工件 的正常加工时间,t为工件
的正常加工时间,t为工件 的开始加工时间,
的开始加工时间, 为学习指数,r为工件
为学习指数,r为工件 所在的序列位置,
所在的序列位置, 为所有工件的退化率,
为所有工件的退化率, 为分配给工件
为分配给工件 的不可再生资源数量,
的不可再生资源数量, 为正参数。文献 [7] [8] [9] 相继研究了带有三种交货期的单机排序问题,其中Sun [10] 中工件
为正参数。文献 [7] [8] [9] 相继研究了带有三种交货期的单机排序问题,其中Sun [10] 中工件 的实际加工时间为
的实际加工时间为 ,目标是极小化带有提前、延误、交货期和资源总费用的和。
,目标是极小化带有提前、延误、交货期和资源总费用的和。
近年来带有工期窗口和资源分配的单机排序问题逐步进入了人们的视野。文献 [11] [12] [13] [14] [15] 所研究问题中,如果一个工件在工期窗口开始之前完工,则相应受到提前惩罚。如果一个工件在工期窗口结束之后完工,则相应接受延误惩罚,如果一个工件在工期窗口之内完工,则无需接受惩罚。本文研究的是工件的加工时间受学习效应、退化效应以及资源分配的影响。所有工件有一个公共工期窗口,我们需要确定最优工期窗口位置以及大小,最优资源分配方案及最优排序。分别考虑了三种情况,第一种是使带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和最小的问题;第二种是资源费用受限的情况下,极小化带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和问题。第三种是在带有提前,延误等总费用受限的情况下,极小化总资源量。证明所研究的三种问题是多项式时间可解的并给出三个最优算法。
2. 问题描述
考虑如下的问题:n个独立且在零时刻到达的工件 需要在一台机器上加工,在同一时刻机器最多只能加工一个工件,所有工件必须连续加工不能中断。本文中凸资源消耗模型中工件
需要在一台机器上加工,在同一时刻机器最多只能加工一个工件,所有工件必须连续加工不能中断。本文中凸资源消耗模型中工件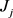 的实际加工时间表达式为
的实际加工时间表达式为

其中 是一个表示分配给工件
是一个表示分配给工件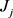 工作量的正参数,m表示一个恒定的正值,
工作量的正参数,m表示一个恒定的正值, 表示学习指数,
表示学习指数, 为分配给工件
为分配给工件 的不可再生的资源数量,r为工件
的不可再生的资源数量,r为工件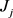 所在位置,工件
所在位置,工件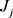 的开始加工时间为
的开始加工时间为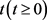 ,
, 为公共退化率。
为公共退化率。
对于给定排序 ,令
,令 表示工件
表示工件 在排序π下的完工时间,
在排序π下的完工时间, ,
, 分别表示最大完工时间和总完工时间。所有的工件有一个公共工期窗口
分别表示最大完工时间和总完工时间。所有的工件有一个公共工期窗口 ,
, 和
和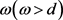 分别表示工期窗口开始时间和结束时间,
分别表示工期窗口开始时间和结束时间,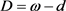 表示工期窗口的大小。如果一个工件在工期窗口开始时间d之前完成,则会导致提前惩罚,另一方面,如果一个工件在工期窗口结束时间ω之后完工,则会造成延误惩罚。对于给定排序
表示工期窗口的大小。如果一个工件在工期窗口开始时间d之前完成,则会导致提前惩罚,另一方面,如果一个工件在工期窗口结束时间ω之后完工,则会造成延误惩罚。对于给定排序 ,我们用
,我们用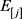 和
和 分别表示提前量和延误量,即
分别表示提前量和延误量,即 ,
,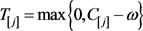 ,其中
,其中 表示工件在排序π下的第j个位置。决策变量为π,d,u,ω。
表示工件在排序π下的第j个位置。决策变量为π,d,u,ω。
问题1:目标是求出最优资源分配 和最优工件排序,最优交货期窗口位置d,ω,使带有提前、延误、工期窗口位置、工期窗口大小、资源总费用,最大完工时间以及总完工时间的总和最小,即目标函数为
和最优工件排序,最优交货期窗口位置d,ω,使带有提前、延误、工期窗口位置、工期窗口大小、资源总费用,最大完工时间以及总完工时间的总和最小,即目标函数为
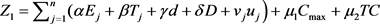
其中 为给定常数。
为给定常数。
问题2:目标是在资源消耗总费用不大于常数 的前提下,求出最优资源分配方案和最优工件排序,最优交货期窗口位置d,ω,使带有提前、延误、工期窗口位置、工期窗口大小、总完工时间、完工时间绝对差的总和最小,即目标函数为
的前提下,求出最优资源分配方案和最优工件排序,最优交货期窗口位置d,ω,使带有提前、延误、工期窗口位置、工期窗口大小、总完工时间、完工时间绝对差的总和最小,即目标函数为
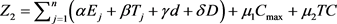
问题3:目标是在 不大于常数
不大于常数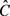 的前提下,决定最优工期窗口
的前提下,决定最优工期窗口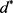 和
和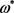 的位置,最优资源分配
的位置,最优资源分配 及最优排序
及最优排序 使总资源消耗量最小,所以目标函数为
使总资源消耗量最小,所以目标函数为

使用文献 [16] 的三参数表示法,可将上述问题分别表示为:
 (1)
(1)
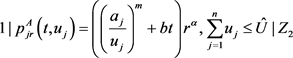 (2)
(2)
 (3)
(3)
3. 最优算法
3.1. 最优解性质
首先在最优排序下,首个工件在0时刻开始加工,工件之间无空闲时间。
引理1:对于排序 ,工件
,工件 的完工时间和实际加工时间分别为
的完工时间和实际加工时间分别为
 (4)
(4)
 (5)
(5)
引理2:对于任何给定排序 ,存在一个最优公共工期窗口,其中工期窗口的开始时间d和结束时间ω与某些工件的完工时间一致。
,存在一个最优公共工期窗口,其中工期窗口的开始时间d和结束时间ω与某些工件的完工时间一致。
证明 存在一个排序π,从0时刻开始加工,
存在一个排序π,从0时刻开始加工,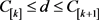 ,
, ,其中
,其中 ,令
,令 ,
, ,则
,则 ,
, 。
。 和
和 分别表示
分别表示 和
和 的实际加工时间。
的实际加工时间。
工件 提前的总费用为
提前的总费用为

工件 延误的总费用为
延误的总费用为
工期窗口开始时间费用为

工期窗口大小费用为

最大完工时间费用为

完工总时间费用为

因此,总费用可以表示为 ,
,
其中, ,
,
 ,
, 为恒定常数,与
为恒定常数,与 无关。为了最小化总成本,下列条件之一成立:
无关。为了最小化总成本,下列条件之一成立:
1) 如果 且
且 ,则
,则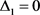 ,
, ;
;
2) 如果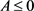 且
且 ,则
,则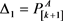 ,
, ;
;
3) 如果 且
且 ,则
,则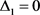 ,
, ;
;
4) 如果 且
且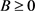 ,则
,则 ,
, 。
。
故我们得到结论:存在一个最优排序,工期窗口的开始时间d和结束时间ω与某些工件的完工时间一致。引理2证毕。
引理3:存在一个最优排序,工期窗口的开始时间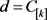 ,其中
,其中 ,工期窗口结束时间
,工期窗口结束时间 ,其中
,其中 。
。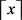 表示不超过x的最大整数。
表示不超过x的最大整数。
证明:详细证明见文献 [17] ,略。
3.2. 最优算法
问题1对于公共工期排序问题,显然,k是独立于排序π与实际加工时间 的,因此,对于问题1我们有
的,因此,对于问题1我们有
 ,
,
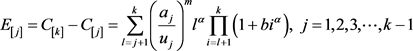
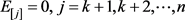 ,
, 

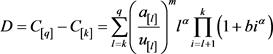




 (6)
(6)
其中
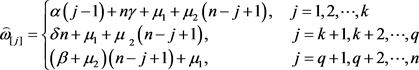 (7)
(7)
且
 (8)
(8)
引理4:问题(1)中对于给定的工件排序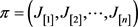 ,最优资源分配为
,最优资源分配为 (9)
(9)
引理5:参考文献 [17] 给定两个数列 和
和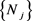 ,
, 。其中一个数列按递增顺序排列,另一个数列按递减顺序排列,则对应元素乘积和
。其中一个数列按递增顺序排列,另一个数列按递减顺序排列,则对应元素乘积和 最小。
最小。
将等式(9)代入到等式(6)中,得到
 (10)
(10)
其中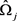 由等式(8)中结果,显然,若使等式(10)中所给的
由等式(8)中结果,显然,若使等式(10)中所给的 极小化等价于极小化
极小化等价于极小化 的值。根据分析以及引理2-5,得到问题(1)的一个算法。
的值。根据分析以及引理2-5,得到问题(1)的一个算法。
算法1
第一步 根据引理2,计算出k与q的值;
第二步 对于 ,计算出
,计算出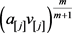 和
和 的值,
的值,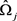 由等式
由等式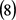 确定;
确定;
第三步 根据引理5得到,最优排序 ;
;
第四步 根据等式(9)计算出最优资源分配 ;
;
第五步 应用等式(5)计算出最优排序中每个工件的加工时间;
第六步 令 ,
, ;
;
第七步 通过等式(10)计算 最优值。
最优值。
定理1:对于问题1):可以通过求解匹配问题在 时间内求得最优解。
时间内求得最优解。
证明:定理结论的正确性由上述分析保证。第一、二、四、五、六步可以在线性时间内完成,
第三步需要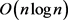 时间内完成,所以算法的时间复杂性为
时间内完成,所以算法的时间复杂性为 。证毕。
。证毕。
问题2):在本部分中,求出问题(2)的最优解
引理6:问题2)对于给定排序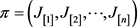 最优资源分配如下:
最优资源分配如下:
 (11)
(11)
证明:对于给定排序,拉格朗日函数为

其中λ为拉格朗日乘子。分别对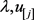 求偏导,令其为零,得
求偏导,令其为零,得
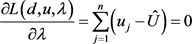 (12)
(12)
 (13)
(13)
利用(12)和(13)得到
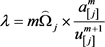 ,
, 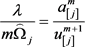 ,
, (14)
(14)
 (15)
(15)
由(14)和(15)我们得到(11)。证毕。
将等式(11)带入到目标函数中,得到
 (16)
(16)
根据上述分析以及引理2-5,得到问题(2)的一个算法。
算法2
第一步 根据引理2,计算出k与q的值;
第二步 对于 。计算出
。计算出 和
和 的值,
的值,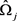 由等式(8)计算得到;
由等式(8)计算得到;
第三步 由引理5得,最优排序 ;
;
第四步 根据等式(9)计算出最优资源分配 ;
;
第五步 应用等式(5)计算出最优排序中每个工件的加工时间;
第六步 令 ,
, ;
;
第七步 通过等式(16)计算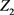 最优值。
最优值。
定理2:对于问题(2)可以通过求解匹配问题在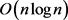 时间内求得最优解。
时间内求得最优解。
证明:类似于定理1证明,从略。
问题(3) 在这个部分里,求出问题(3)的最优解。首先,与引理6类似,有
引理7:问题(3)对于给定排序 可以得到最优资源分配如下:
可以得到最优资源分配如下:
 (17)
(17)
将式(17)代入 中,得
中,得
 (18)
(18)
根据上述分析以及引理2-5,得到问题(3)的一个算法。
算法3
第一步 根据引理2,计算出k与q的值;
第二步 对于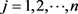 。计算出
。计算出 和
和 的值,
的值,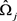 由等式(8)计算得到;
由等式(8)计算得到;
第三步 根据引理5得,最优排序 ;
;
第四步 根据等式(17)计算出最优资源分配 ;
;
第五步 应用等式(5)计算出最优排序中每个工件的加工时间;
第六步 令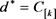 ,
, ;
;
第七步 通过等式(18)计算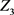 最优值。
最优值。
定理3:对于问题(3)可以通过求解匹配问题在 时间内求得最优解。
时间内求得最优解。
证明:类似于定理1证明,从略。
4. 结论
本文研究的是具有学习效应和退化效应且加工时间是关于资源的凸函数并且带有公共工期窗口的问题。本文列举了三种问题,第一种是使带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和最小的问题;第二种是资源费用受限的情况下,极小化带有提前,延误,公共工期开始时间,工期窗口大小,资源成本费用,最大完工时间以及总完工时间和问题。第三种是在带有提前,延误等总费用受限的情况下,极小化总资源量。我们分别给出了目标函数求得最小值的最优算法,并证明问题是多项式时间可解的,并确定最优排序及最优资源分配,将问题转化为匹配问题证明问题在多项式时间內可解,并给出了相应的多项式时间算法。
基金项目
国家自然科学基金资助项目(11171050)。
文章引用
李 石,罗成新. 带有工期窗口和凸资源分配的单机排序问题
Single-Machine Scheduling with Due-Window Assignment and Convex Resource Allocation[J]. 应用数学进展, 2018, 07(04): 446-455. https://doi.org/10.12677/AAM.2018.74055
参考文献
- 1. Biskup, D. (2008) A State-of-the-Art Review on Scheduling with Learning Effect. European Journal of Operational Research, 188, 315-329. https://doi.org/10.1016/j.ejor.2007.05.040
- 2. Gawiejnowicz, S. (2008) Time-Dependent Scheduling. Springer, Berlin.
- 3. Shabtay, D. and Steiner, G. (2007) A Survey of Scheduling with Controllable Processing Times. Discrete Applied Mathematics, 155, 1643-1666. https://doi.org/10.1016/j.dam.2007.02.003
- 4. Wang, X.-R. and Wang, J.-J. (2013) Single-Machine Scheduling with Convex Resource Dependent Processing Times and Deteriorating Jobs. Applied Mathematical Modelling, 37, 2388-2393. https://doi.org/10.1016/j.apm.2012.05.025
- 5. Wang, X.-Y. and Wang, J.-J. (2013) Single-Machine Due Date Assignment Problem with Deteriorating Jobs and Resource-dependent Processing Times. International Journal of Advanced Manufacturing Technology, 67, 255-260. https://doi.org/10.1007/s00170-013-4771-x
- 6. Wang, J.B., Wang, M.Z. and Ji, P. (2012) Scheduling Jobs with Processing Times Dependent on Position, Staring Time and Allotted Resource. Asia-Pacific Journal of Operational Research, 29, 1250030.
- 7. Lu, Y.-Y., Li, G., Wu, Y.-B. and Ji, P. (2014) Optimal Due-Date Assignment Problem with Learning Effect and Resource-Dependent Processing Times. Optimization Letters, 8, 113-127. https://doi.org/10.1007/s11590-012-0467-7
- 8. Cheng, T.C.E., Kang, L.Y. and Ng, C.T. (2004) Due-Date Assignment and Single Machine Scheduling with Deteriorating Jobs. Journal of the Operational Research Society, 55, 198-203. https://doi.org/10.1057/palgrave.jors.2601681
- 9. Gordon, V.S. and Tarasevich, A.A. (2009) A Note: Common Due Date Assignment for a Single Machine Scheduling with the Rate-Modifying Activity. Computers & Operations Research, 36, 325-328. https://doi.org/10.1016/j.cor.2007.10.008
- 10. Sun, L.-H., Cui, K., Chen, J.-H. and Wang, J. (2016) Due Date Assignment and Convex Resource Allocation Scheduling with Variable Job Processing Times. International of Production Research, 54, 3551-3560. https://doi.org/10.1080/00207543.2015.1083628
- 11. Li, G., Luo, M.L., Zhang, W.J. and Wang, X.Y. (2015) Single-Machine Due-Window Assignment Scheduling Based on Flow Allowance, Learning Effect and Resource Allocation. International Journal of Production Research, 53, 1228-1241. https://doi.org/10.1080/00207543.2014.954057
- 12. Wu, Y.-B., Wan, L. and Wang, X.-Y. (2015) Study on Due-Window Assignment Scheduling Based on Common Flow Allowance. International Journal of Production Economics, 165, 155-157. https://doi.org/10.1016/j.ijpe.2015.04.005
- 13. Wang, J.B. and Wang, J.J. (2015) Research on Scheduling with Job-Dependent Learning Effect and Convex Resource-Dependent Processing Times. International Journal of Production Research, 53, 5826-5836. https://doi.org/10.1080/00207543.2015.1010746
- 14. Wang, J.-B., Liu, M.-Q., Yin, N. and Ji, P. (2017) Scheduling Jobs with Controllable Processing Time, Truncated Job-Dependent Learning and Deteriortion Effects. Journal of Industrial and Management Optimization, 13, 1025-1039.
- 15. Mor, B. and Mosheiov, G. (2012) Scheduling a Maintenance Activity and Due Window Assignment Based on Common Flow Allowance. International Journal of Production Economics, 135, 222-230. https://doi.org/10.1016/j.ijpe.2011.07.013
- 16. Graham, R.L., Lawler, E.L., Lenstra, J.K. and Rinnooy Kan, A.H.G. (1979) Optimization and Approximation Indeterministic Sequencing and Scheduling. A Survey. Annals of Discrete Mathematics, 5, 287-326. https://doi.org/10.1016/S0167-5060(08)70356-X
- 17. Hardy, G.H., Littlewood, J.E. and Polya, G. (1967) Inequalities. Cambridge University Press, Cambridge.