Advances in Applied Mathematics
Vol.07 No.07(2018), Article ID:26142,15
pages
10.12677/AAM.2018.77108
CT System Parameter Calibration and Imaging
Hong Yang, Zhengtai Ma, Wenwen Ju
Minzu University of China, Beijing

Received: Jul. 6th, 2018; accepted: Jul. 23rd, 2018; published: Jul. 30th, 2018

ABSTRACT
Aiming at the parameter calibration and imaging problem of CT system, this paper realizes the calibration of CT system parameters and the information of unknown medium through geometric analysis and graph reconstruction algorithm, and uses the accuracy and stability of parameter calibration to determine the better CT calibration template. We first analyze the relationship of the data and find the distance between the detector units, then establish a reasonable Cartesian coordinate system and use the geometric knowledge of the ellipse to calibrate the parameters of the CT system. In order to reconstruct the unknown image, we chose the filtered back projection algorithm (FBP) and the algebraic reconstruction algorithm (ART) to get information about the unknown medium and the absorption rate of 10 points. We use the original pattern and the reconstructed image of the calibration template to calculate the relative error of the distance between two points and the standard error of the CT value, so as to analyze the accuracy and stability of the calibration template. In order to improve it, based on the Caphan phantom, a new calibration template was established. After verification, the accuracy and stability of the calibration of the new template parameters have been improved.
Keywords:CT System, Parameter Calibration, Image Reconstruction, Filtered Back Projection Algorithm, Algebraic Reconstruction Algorithm
CT系统的参数标定及成像
杨宏,马正泰,巨雯雯
中央民族大学,北京

收稿日期:2018年7月6日;录用日期:2018年7月23日;发布日期:2018年7月30日

摘 要
针对CT系统的参数标定和成像问题,本文通过几何分析、图形重建算法实现了CT系统的参数标定和未知介质相关信息的确定,并利用参数标定的精度和稳定性确定更优的CT标定模板。我们首先分析了数据的关系,求得探测器单元之间的距离。然后建立合理的直角坐标系,利用椭圆的几何知识标定CT系统的参数。为了对未知图形进行重建,我们选择了滤波反投影算法(FBP)和代数重建算法(ART)。得到未知介质的相关信息以及10个点的吸收率。我们利用标定模板的原图形和重建图形,计算某两点间距离的相对误差和CT值的标准误差,从而分析标定模板的精度和稳定性。为了对其进行改进,在Caphan体模的基础上,确定了一个新的标定模板。经验证,新模板参数标定的精度和稳定性都有所提高。
关键词 :CT系统,参数标定,图像重建,滤波反投影算法,代数重建算法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 问题的提出与分析
1.1. 问题的提出
CT (Computed Tomography)可以在不破坏样品的情况下,利用样品对射线能量的吸收特性获取样品内部的结构信息。本题中,我们考虑一种典型的二维CT:
1) 平行入射的X射线垂直于探测器平面,每个探测器单元看成一个接收点且等距排列。2) X射线的发射器和探测器相对位置保持不变,整个系统绕某固定的旋转中心逆时针旋转180次。3) 对每一个X射线方向,在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到180组接收信息。
CT系统安装时往往存在误差,为了保证成像质量,因此需要对安装好的CT系统进行参数标定,即借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像。
1) 在正方形托盘上放置两个均匀固体介质组成的标定模板,利用该模板的几何信息和接受信息确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。
2) 基于(1)中得到的标定参数,利用上述CT系统得到的某未知介质的接收信息,确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息以及题中表3所给的10个位置处的吸收率。
3) 利用上述CT系统得到的另一未知介质的接收信息,确定该未知介质的相关信息10个位置处的吸收率。
4) 分析(1)中参数标定的精度和稳定性。在此基础上自行设计新模板、建立对应的标定模型,以改进标定精度和稳定性,并说明理由。
1.2. 问题的分析
1.2.1. 问题一:利用几何关系求得模板的参数信息
首先我们通过对比分析附录1和附录2中的数据,找到它们之间的对应关系。之后根据表格中接收信息的探测器个数与小圆直径的比例关系求得探测器单元之间的距离。然后建立合理的坐标系,利用椭圆的几何平面知识与切线之间关系求解X射线的方程,多条射线的交点即可确定CT系统的旋转中心,射线的斜率即射线与X轴夹角的正切值,进而推算出X射线的180个方向。
1.2.2. 问题二:利用图形重建算法确定未知介质信息
为了得到某未知介质的相关信息,就需要利用该介质的CT接收信息对图形进行重建。本题中我们选择了两种常用的图形重建方法:滤波反投影算法和代数重建算法。接着以问题一中的标定模板为例,通过对CT重建图像的噪声分析,比较两种重建方法的精度,得出较优的方法。然后用该方法进行模型求解得到重建图像,最后求出问题二中未知介质的位置、几何形状和吸收率等信息。
1.2.3. 问题三:利用图形重建算法确定未知介质信息
在问题二的基础上,用滤波反投影算法对另一未知介质进行了图形重建,由此得到该未知介质的相关信息和图3具体十个位置处的吸收率。
1.2.4. 问题四:分析精度和稳定性并改进标定模板
我们结合原图形和重建图形,通过分析、计算某两点之间距离的相对误差和CT值的标准误差,进而得到问题一中参数标定的精度和稳定性。为了提高CT机参数标定的精度和稳定度,我们以Catphan体模为基础,确定了新的标定模板并对其精度和稳定度进行检验。
2. 模型假设
1) 假设CT系统平行入射的X射线光子波动不明显,忽略衍射现象。
2) 假设整个CT系统只有探测单元发出X射线,忽略X射线的光子能量发生电子对效应产生的X射线。
3) 假设题目所给的数据收集于正常工作的CT系统,且能反映实际情况。
4) 假设X射线源焦点和探测器单元为质点。
3. 符号说明
图1是文中所用到的符号说明。
4. 模型的建立与求解
4.1. 问题一
分析题目可知,本题研究的是一种二维CT系统,它是利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像。附录1是两个均匀介质组成的标定模板的吸收率数据,与之对应的附录2是用二维CT系统测量的接收信息,由此可以由吸收率和接收信息的对应关系得到CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。
4.1.1. 探测器单元距离的确定
通过对附录2中180个探测方向接收信息的数据分析得到图2。
180个探测方向经过均匀的小圆介质时的有接收信息的探测器个数N固定,即:
由已知标定模板的几何信息可得到小圆介质的直径
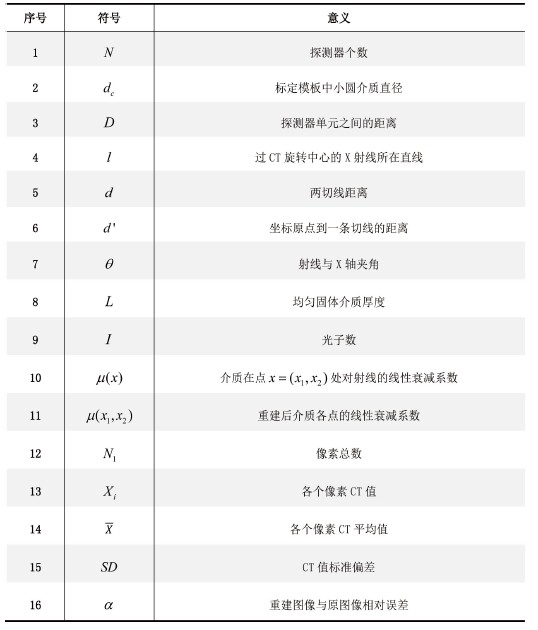
Figure 1. Symbol description
图1. 符号说明图
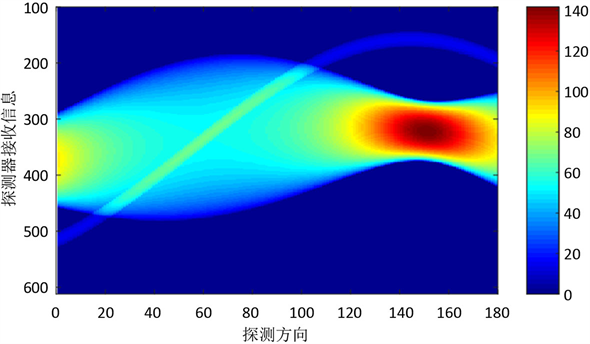
Figure 2. Schematic diagram of receiving direction information
图2. 探测方向接收信息示意图
平行入射的X射线垂直于探测器平面,每个探测器单元看成一个接收点,且等距排列。由
(1)
解得,探测器单元之间的距离
4.1.2. 旋转中心和X射线180个方向的确定
以正方形托盘的几何中心为坐标原点O,以椭圆的长轴为y轴,椭圆的短轴为x轴,在标定模板上建立如图3所示坐标系:
设O'点为旋转中心,且某一过CT旋转中心的射线所在直线为: 。
当斜率为k的多条X射线射入椭圆时,记与椭圆相切的两条直线为 , 。记两切线的距离为d。坐标原点到一条切线的距离为d',与x轴夹角为 。利用两切线距离和椭圆方程联立方程组
(2)
得到切点 ,进而得到切线的斜率k和与x轴的夹角
(3)
进而求得一条切线方程为
(4)
1) 求旋转中心的确定
为了减小误差,我们将探测得到的180个数据采用系统抽样的方法选取20条不同方向的角度数据(表1)。
通过上述方法求得20条切线,两两求其交点,然后计算横纵坐标的平均值,得到旋转中心为(−9.2427, 5.7939)。
2) X射线180个方向的确定
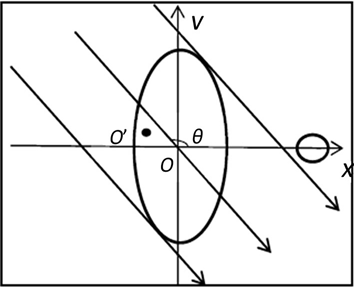
Figure 3. Coordinate system
图3. 坐标系示意图
通过上述方法求得各个方向的射线与x轴的夹角 ,然后求相邻两个角度的差即为转动一次所转的角度。最终得到如下表2所示的该CT系统使用的X射线的180个方向。该方向表示该次旋转的X射线与所建立坐标系x轴的夹角(图4)。
由以上数据可以得出,X射线的每次探测所转的角度并不均匀,180次探测总共转过了179.0247°,平均每次绕逆时针旋转0.9946°。
4.2. 问题二
CT图像重建算法有二维傅里叶变换法、反投影法、迭代法、拟合逼近法等,其中较常用的有反投影法中的滤波反投影算法(FBP)和代数重建算法(ART) [1] 。基于问题一的模板,我们用这两种方法对图形进行重建,然后比较这两种算法的优劣,选择一种较优方法解决问题二。
Table 1. 20 public tangential angles
表1. 20条公切线倾斜角
Table 2. CT system rotation angle
表2. CT系统旋转角度
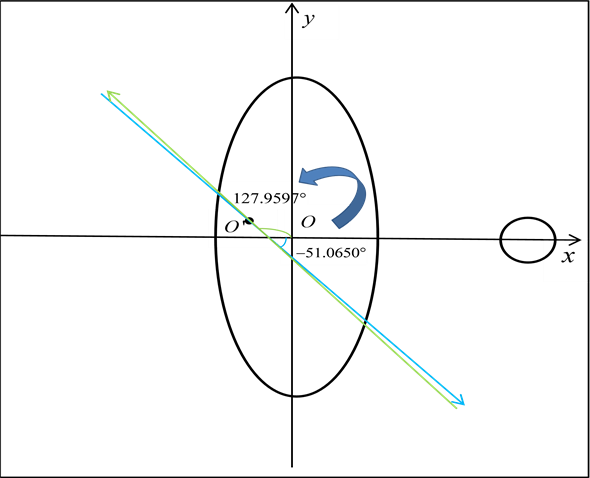
Figure 4. CT system rotation
图4. CT系统旋转示意图
4.2.1. 平行束投影及其反演
在理想条件下,探测器的射线穿过厚度为L的均匀固体介质后,由Beer-Lambert定律知,探测器探测到的光子数I满足 [2] :
(5)
若介质分布不均匀,则用 表示介质在点 处对射线的线性衰减系数,通过积分得
(6)
CT反演问题:利用CT系统的平行束射线探测未知介质,得到未与介质作用的光子数,进而重建介质各点的线性衰减系数 的值。因为线性衰减系数与介质的厚度和密度有线性关系,所以可以反映出未知介质的几何形状。
4.2.2. 滤波反投影算法(FPB)
滤波反投影算法的基础是中心切片定理和傅里叶变换法。
1)中心切片定理
密度函数 在某一方向上的投影函数 的一维傅立叶变换函数, 是原密度函数 的二位傅里叶函数 在 平面沿同一方向的直线上的值。
2)傅里叶变换法
极坐标形式的二维逆傅里叶变换为
(7)
其中
(8)
重建公式
(9)
其中 , , 是窗口函数。
滤波反投影的重建公式为
(10)
其中 是 关于变量r的Fourier变换,即
(11)
采用滤波反投影算法(FPB),结合Matlab编程(程序见附录)可以利用所接收的信息重建标定模板的CT图像,如图5。
4.2.3. 代数重建算法(ART)
代数重建算法重建CT图像的主要步骤:
1) 对X赋值
2) 沿逐条射线迭代
(12)
3) 反复计算(2)式,直到满足一定的收敛条件,比如判断 是否小于给定的阈值 [3] 。
采用代数重建算法(ART),结合Matlab编程(程序见附录)可以利用附录2所给的接收信息重建标定模板的CT图像,如图6。
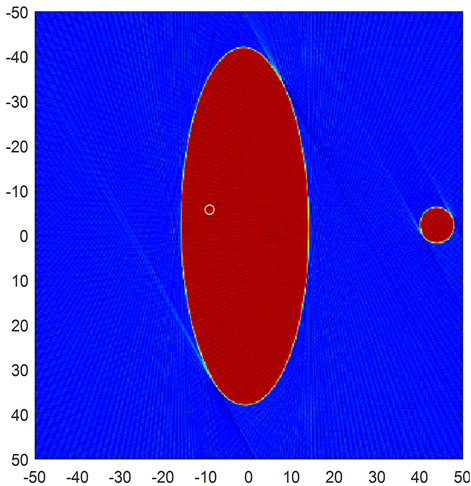
Figure 5. CT image of FPB reconstruction calibration template
图5. FPB重建标定模板的CT图像
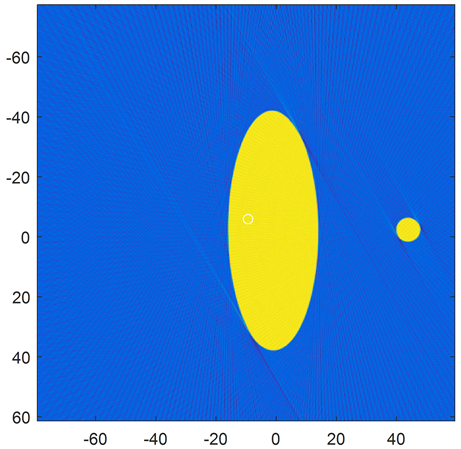
Figure 6. CT image of calibration template by algebraic reconstruction algorithm
图6. 代数重建算法标定模板的CT图像
4.2.4. CT重建图像噪声分析
噪声是指在均匀物体影像中CT值在平均值上下的随机涨落,其数值可用CT值的标准偏差SD表示
(13)
其中 为像素总数, 为每个像素的CT值, 为所有像素CT值的平均值。
利用滤波反投影算法求得:
平均像素 方差 ;
利用代数重建算法求得:平均像素 ,方差
由此可以看出利用FBP反演公式的SD值较小,CT值曲线变化波动较小,重建后的图像的噪声较小(图7)。
4.2.5. 模型求解
通过CT系统重建图像噪声分析可以得出滤波反投影算法,T值曲线变化波动较小,重建后的图像的噪声较小,故将附录3未知介质的接收信息采用滤波反投影算法得到如下的重建图像:
如图8所示,该介质放置于 的正方形模板上,CT旋转中心位于图中白圈所在的位置,图中越偏暖色,吸收强度越强,此处介质密度也越大。该介质在该断层面面呈椭圆形,其中存在两个椭圆形空腔,两个密度较大的椭圆状部分。10个位置处的吸收率如表3所示,该介质的吸收率附在数据文件problem2.xls。
4.3. 问题三
附录5是利用上述CT系统得到的另一个未知介质的接收信息。通过CT系统重建图像噪声分析可以得出滤波反投影算法,重建后的图像的噪声较小,故将附录5未知介质的接收信息采用滤波反投影算法得到如下的重建图像:
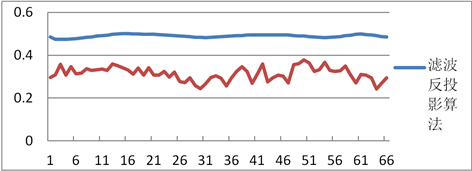
Figure 7. CT value curve
图7. CT值变化曲线

Figure 8. Problem 2 reconstruction image
图8. 问题二重建图像
Table 3. Absorption rates at 10 locations in question 2
表3. 问题二中10个位置的吸收率
如图9所示,该介质放置于 的正方形模板上,CT旋转中心位于图中白圈所在的位置,图中越偏暖色,吸收强度越强,此处介质密度也越大。该介质未知介质断层的形状不规则,每点的吸收率分布不均匀。10个位置处的吸收率如表4所示,该介质的吸收率附在数据文件problem3.xls。
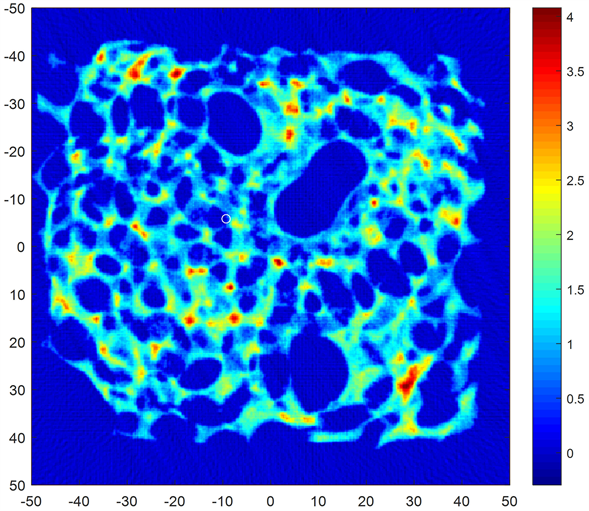
Figure 9. Problem 3 reconstructed image
图9. 问题三重建图像
Table 4. Absorption rates at 10 locations in problem 3
表4. 问题三中10个位置的吸收率
4.4. 问题四
4.4.1. 问题一中参数标定的精度
为了得到问题一中参数标定的误差,我们以原标定模板中的椭圆和圆的两个中心的距离 为参考。通过问题一中的重建公式,可以得到利用滤波反投影算法重建后图像的椭圆和圆中心的坐标,进而求得两个中心的距离 。从而得到重建图像和原图像的相对误差
问题一得 , , 。相对误差小于1%,参数标定的精度较高。
4.4.2. 问题一中参数标定的稳定性
为了判断参数标定的稳定性,我们利用刻画均匀物体影像中CT值在平均值上下的随机涨落的噪声指标,其数值可用CT值的标准偏差SD表示
(14)
其中N为像素总数, 为每个像素的CT值, 为所有像素CT值的平均值。
利用滤波反投影算法所求得平均像素 ,方差 。
4.4.3. 设定新的标定模板
在CT成像系统的接收过程中,必定存在误差。其中误差主要来源于机械误差的精度以及利用标定模板,在成像过程中获取像素坐标时引起的误差。为了改进参数标定的精度和稳定性,我们在Catphan体模的基础上加以改进,得到如下图10所示的新的标定模板。
得 , , , 。
新模板的相对误差较原模板的小,因此新模板的参数标定的精度较高,稳定性更高(表5)。
5. 模型优缺点分析
5.1. 优点
1) 滤波反投影算法(FBP):数学形式较为简单,应用广泛,容易达到预期效果,在锥角较小、扫描半径较大情况下能够取得较好的重建效果。
2) 代数重建算法(ART):适合不完全投影数据的图像重建,当投影数据不完整时可以把缺失的数据看成是缺少了几个方程,这在某种程度上忽略了数据不全的问题。因而适用于不能获得完整投影数据的图像重建。且重建质量好,尤其是在投影数据较少的情况下。重建算法简单,适用于对不同格式的采样数据重建。缺点是计算量大,重建速度较慢。
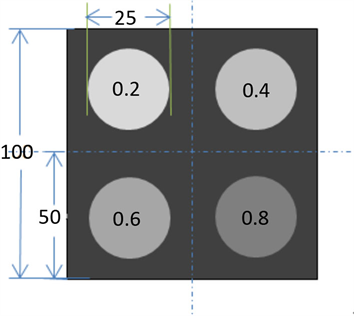
Figure 10. New calibration template
图10. 新的标定模板
Table 5. Comparison of the two calibration tables
表5. 两种标定表格的对比
5.2. 缺点
ART当投影数据不完整时可以把缺失的数据看成是缺少了几个方程。这在某种程度上忽略了数据不全的问题。因而适用于不能获得完整投影数据的图像重建。缺点是重建速度较慢。
文章引用
杨宏,马正泰,巨雯雯. CT系统的参数标定及成像
CT System Parameter Calibration and Imaging[J]. 应用数学进展, 2018, 07(07): 903-917. https://doi.org/10.12677/AAM.2018.77108
参考文献
- 1. 骆岩红. CT图像重建滤波反投影算法中指数滤波器的研究[J]. 计算机科学, 2014, 41(S1): 220-223.
- 2. 张朋, 张慧滔, 赵云松. X射线CT成像的数学模型及其有关问题[J]. 数学建模及其应用, 2012, 1(1): 1-12.
- 3. 王洋, 夏顺仁, 汪元美. X射线CT模型及重建算法[J]. 计算机工程与应用, 2005(4): 220-222, 229.
附录
附录1:滤波反投影算法(FPB)Matlab程序
xc =-5.7939; yc =-9.2427;
phantom = load('3.dat');%信息数据文件
phantom = [zeros(100,180); phantom; zeros(100,180)];
imagesc(phantom)
figure
img = iradon(phantom,[0:179]+30);
n = size(img,1);
[x,y]=meshgrid([-n/2:n/2]*0.2759);
imagesc(x(1,:)-10, y(:,1)-8, img)
hold on
plot(yc,xc,'ow')
axis image
附录2:代数重建算法(ART)Matlab程序
clc;
clear all;
close all;
N = 256;
N2 = N^2;
I=load('22.dat');
theta = linspace(0,180,181);
theta = theta(1:180);
P_num =512;
P=load('22.dat');
delta = 1;
[W_ind,W_dat] = SystemMatrix(theta,N,P_num,delta);
F = zeros(N2,1);
lambda = 0.25;
c = 0;
irt_num = 5;
while(c
for j = 1:length(theta)
for i = 1:1:P_num
u = W_ind((j-1)*P_num + i,:);
v = W_dat((j-1)*P_num + i,:);
if any(u) == 0
continue;
end
w = zeros(1,N2);
ind = u > 0;
w(u(ind))=v(ind);
PP = w * F;
C = (P(i,j)-PP)/sum(w.^2) * w';
F = F + lambda * C;
end
end
F(F<0) = 0;
c = c+1;
end
F = reshape(F,N,N)';
figure(1);
imagesc(I);xlabel('(a)信息数据图像');
figure(2);
A = imadjust(F);
imshow(F);xlabel('(b)ART算法重建的图像');
