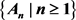ABSTRACT

Given a stochastic process $\left\{A_n|n\ge 1\right\}$, taking values in natural number. Analog to the continued fractions of real numbers, the random continued fraction $X:=\left[A_1,A_2,\cdots ,A_n,\cdots \right]$ is defined. This paper shows that its convergent converges to X almost surely by the nest theorem for intervals. The large deviation estimate is also considered for the Lévy constant of the denominator of the convergents. When $\left\{A_n|n\ge 1\right\}$ is i.i.d., the lower bound for the corresponding probability is given. At the end, the exact lower bounds for Poission distribution, geometric process etc. are obtained.

Keywords:Random Continued Fraction, Convergent, Deviation Estimate

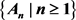
随机连分数收敛因子的收敛性和大偏差估计

谢胜寒

华南理工大学数学学院，广东 广州

收稿日期：2020年5月1日；录用日期：2020年5月19日；发布日期：2020年5月26日

摘 要

给定取值于自然数集的随机过程 $\left\{A_n|n\ge 1\right\}$，类似于实数的连分数展式来定义随机连分数 $X:=\left[A_1,A_2,\cdots ,A_n,\cdots \right]$，本文通过区间套定理证明了其收敛因子几乎必然地收敛到X，并对收敛因子的分母对应的Lévy常数进行了大偏差估计，在 $\left\{A_n|n\ge 1\right\}$ 满足独立同分布时，给出了相应概率的下界估计，对泊松分布、几何分布等特殊情形给出了具体的下界数值。

关键词 :随机连分数，收敛因子，偏差估计

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 研究背景及主要结果

连分数是表示实数的一种重要方式，其数学方面的研究自欧拉时代就开始了，其在数论如丢番图逼近中发挥着重要作用，近些年来与概率论、分形几何、动力系统等学科建立了紧密的联系。连分数的基本知识和度量结果可参考Khintchine [1]，刘鹏 [2]，其Lévy常数相关内容可以参考Faivre [3]。

2015年，Fang等 [4] 引入了随机连分数。令 $\left(\Omega ,\mathcal{F},P\right)$ 为概率空间， $\left\{A_n|n\ge 1\right\}$ 是定义在 $\left(\Omega ,\mathcal{F},P\right)$ 上的一个随机过程；它在测度空间 $\left({\mathbb{N}}_{+},\mathcal{C}\right)$ 中取值，其中 ${\mathbb{N}}_{+}$ 是自然数集， $\mathcal{C}$ 是 ${\mathbb{N}}_{+}$ 的幂集。对任意 $\omega \in \Omega$，我们定义 [4]

$X\left(\omega \right):=\left[A_1\left(\omega \right),A_2\left(\omega \right),\cdots ,A_n\left(\omega \right),\cdots \right]=\frac{1}{A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_n\left(\omega \right)+\cdots }}},$

我们称X是由随机过程 $\left\{A_n|n\ge 1\right\}$ 生成的随机连分数。

对 $\forall \omega \in \Omega$ 及 $P_n$，$P_n$ 及 $Q_n$ 定义如下 [4]：

$\frac{P_n\left(\omega \right)}{Q_n\left(\omega \right)}:=\left[A_1\left(\omega \right),A_2\left(\omega \right),\cdots ,A_n\left(\omega \right)\right]=\frac{1}{A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_n\left(\omega \right)}}},$

其中 $P_n\left(\omega \right)$ 及 $Q_n\left(\omega \right)$ 为互素的正整数。我们称 $\frac{P_n}{Q_n}$ 为X的第n个收敛因子。这里 $P_n\left(\omega \right)$ 和 $Q_n\left(\omega \right)$ 也可以通过归纳的方式来得到。

$P_n=A_n{P}_{n-1}+P_{n-2},\forall n\in {\mathbb{N}}_{+}$，其中 $P_{-1}=1,P_0=0$。

$Q_n=A_n{Q}_{n-1}+Q_{n-2},\forall n\in {\mathbb{N}}_{+}$，其中 $Q_{-1}=0,Q_0=1$。

我们首先研究收敛因子 $\frac{P_n}{Q_n}$ 的收敛性，得到如下结果。

定理1：记 $\left\{A_n|n\ge 1\right\}$ 是一个取值于自然数集的随机过程，则几乎必然地其收敛因子收敛到X，即

$\frac{P_n\left(\omega \right)}{Q_n\left(\omega \right)}\stackrel{a.e.}{\to }X\left(\omega \right),n\to \infty .$

收敛因子的分母 $Q_n$ 在连分数研究中起着重要作用。

定义1：上极限 $\lim {\sup }_{n\to \infty }\frac{1}{n}\log Q_n$ 和下极限 $\lim {\inf }_{n\to \infty }\frac{1}{n}\log Q_n$ 分别称为X的上、下Lévy常数，若极限 ${\lim }_{n\to \infty }\frac{1}{n}\log Q_n$ 存在，则其极限值称为X的Lévy常数。

Fang等 [4] 证明了当 $\left\{A_n|n\ge 1\right\}$ 是遍历的且随机变量 $\log A_1$ 的数学期望有限，即 $E\left(\log A_1\right)<\infty$ 时，几乎必然有

$\underset{n\to \infty }{\lim }\frac{1}{n}\log Q_n=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}.$

也就是说，Lévy常数几乎必然存在且为一个常数，特别地，该收敛也是依概率收敛的，即对任意 $\delta >0$，

${\lim }_{n\to \infty }P\left(\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right)=0.$ (1)

他们对上述收敛速度进行了研究，得到了Chernoff型的上界估计。

定理2 [4]：假设 $\left\{A_n|n\ge 1\right\}$ 是 $\psi$ -混合的且对任意 $0<t<1$ 有 $E\left(A_1^t\right)<\infty$，则对任意 $\delta >0$，存在 $N>0,B>0,\alpha >0$ 使得

$P\left(\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right)\le B{\text{e}}^{-\alpha n}.$

上述结果作为关于 $\frac{1}{n}\log Q_n$ 收敛的大偏差估计并不完整，因为只有上界估计，作为该结果的补充，我们给出当 $\left\{A_n|n\ge 1\right\}$ 独立同分布时的下界估计。

定理3：记 $\left\{A_n|n\ge 1\right\}$ 是一个取值于自然数集独立同分布的随机过程，记 $P\left(A_1=k\right)=f\left(k\right),k\in {\mathbb{N}}_{+},$

则

$P\left(\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right)\ge {\left(1-F\left({\text{e}}^{b+\delta }\right)\right)}^n,$

其中 $b=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}$，$F\left(x\right)=P\left(A_1\le x\right)$ 为随机变量 $A_1$ 的分布函数。

该定理表明，上述(1)中的收敛有指数的下界，结合 [1] 中的结果，我们知道 $P\left(\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right)$ 是具有指数型偏差的，在本文的第三部分，我们将对泊松分布、几何分布等特殊情形给出了具体的下界数值。大偏差及概率的相关知识可参看Durret [5]。

2. $\frac{P_n\left(\omega \right)}{Q_n\left(\omega \right)}$ 的收敛性的证明

我们用区间套定理给出定理1的完整证明。

定理1的证明：记 $X_n\left(\omega \right)\triangleq \frac{P_n\left(\omega \right)}{Q_n\left(\omega \right)}$，考虑 $\left\{X_n\left(\omega \right)\right\}$ 的两个子列 $\left\{X_{2n-1}\left(\omega \right)|n\in {\mathbb{N}}_{+}\right\}$ 及 $\left\{X_{2n}\left(\omega \right)|n\in {\mathbb{N}}_{+}\right\}$。

第一步，我们证明， $\forall n_1,n_2\in {\mathbb{N}}_{+},X_{2n_1-1}\left(\omega \right)>X_{2n_2}\left(\omega \right)$。若 $2n_1-1<2n_2$，则有

$X_{2n_1-1}\left(\omega \right)=\frac{1}{A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_1-1}\left(\omega \right)}}},$

$X_{2n_2}\left(\omega \right)=\frac{1}{A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_1-1}\left(\omega \right)+\cdots +\frac{1}{A_{2n_2}\left(\omega \right)}}}}.$

由于 $\forall n\in {\mathbb{N}}_{+},A_n\left(\omega \right)\in {\mathbb{N}}_{+}$，故

$A_{2n_1}\left(\omega \right)+\cdots +\frac{1}{A_{2n_2}\left(\omega \right)}>0,$

因此

$A_{2n_1-1}\left(\omega \right)<A_{2n_1-1}\left(\omega \right)+\frac{1}{A_{2n_1}\left(\omega \right)+\cdots +\frac{1}{A_{2n_2}\left(\omega \right)}},$

从而

$A_{2n_1-2}\left(\omega \right)+\frac{1}{A_{2n_1-1}\left(\omega \right)}>A_{2n_1-2}\left(\omega \right)+\frac{1}{A_{2n_1-1}\left(\omega \right)+\cdots +\frac{1}{A_{2n_2}\left(\omega \right)}}.$

仿照上面两步的推导过程，经过 $2n_1-2$ 步后，我们有

$\frac{1}{X_{2n_1-1}\left(\omega \right)}=A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_1-1}\left(\omega \right)}}<A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_2}\left(\omega \right)}}=\frac{1}{X_{2n_2}\left(\omega \right)},$

因此 $X_{2n_1-1}\left(\omega \right)>X_{2n_2}\left(\omega \right)$。同理可知，当 $2n_1-1>2n_2$ 时， $X_{2n_1-1}\left(\omega \right)>X_{2n_2}\left(\omega \right)$ 亦成立。从而 $\forall n\in {\mathbb{N}}_{+},\left[X_{2n}\left(\omega \right),X_{2n+1}\left(\omega \right)\right]$ 构成 $\left[0,1\right]$ 内的一个区间。

第二步，我们证明， $\left\{X_{2n-1}\left(\omega \right)\right\}$ 关于n单调递减， $\left\{X_{2n}\left(\omega \right)\right\}$ 关于n单调递增。不妨取 $n_1,n_2\in {\mathbb{N}}_{+},n_1<n_2$，由第一步当中的证明过程可知，

$A_{2n_1-1}\left(\omega \right)<A_{2n_1-1}\left(\omega \right)+\frac{1}{A_{2n_1}\left(\omega \right)+\cdots +\frac{1}{A_{2n_2-1}\left(\omega \right)}},$

从而

$\frac{1}{X_{2n_1-1}\left(\omega \right)}=A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_1-1}\left(\omega \right)}}<A_1\left(\omega \right)+\frac{1}{A_2\left(\omega \right)+\cdots +\frac{1}{A_{2n_2-1}\left(\omega \right)}}=\frac{1}{X_{2n_2-1}\left(\omega \right)},$

因此 $X_{2n_1-1}\left(\omega \right)>X_{2n_2-1}\left(\omega \right)$。类似可证 $X_{2n_1}\left(\omega \right)<X_{2n_2}\left(\omega \right)$。从而 $\left\{\left[X_{2n}\left(\omega \right),X_{2n+1}\left(\omega \right)\right]|n\in {\mathbb{N}}_{+}\right\}$ 是一个渐缩的区间套。

第三步， $X_{2n+1}\left(\omega \right)-X_{2n}\left(\omega \right)\to 0,n\to \infty$。首先，

$\begin{array}{c}{X}_3\left(\omega \right)-X_2\left(\omega \right)=\frac{1}{A_1+\frac{1}{A_2+\frac{1}{A_3}}}-\frac{1}{A_1+\frac{1}{A_2}}=\frac{\frac{1}{A_2+\frac{1}{A_3}}-\frac{1}{A_2}}{\left(A_1+\frac{1}{A_2+\frac{1}{A_3}}\right)\left(A_1+\frac{1}{A_2}\right)}\\ =\frac{\frac{\frac{1}{A_3}}{\left(A_2+\frac{1}{A_3}\right)A_2}}{\left(A_1+\frac{1}{A_2+\frac{1}{A_3}}\right)\left(A_1+\frac{1}{A_2}\right)}=\frac{\frac{1}{\left(A_2+\frac{1}{A_3}\right)A_2}}{\left(A_1+\frac{1}{A_2+\frac{1}{A_3}}\right)\left(A_1+\frac{1}{A_2}\right)}\cdot \frac{1}{A_3}\\ =\frac{\frac{1}{A_2+\frac{1}{A_3}}}{A_1+\frac{1}{A_2+\frac{1}{A_3}}}\cdot \frac{\frac{1}{A_2}}{A_1+\frac{1}{A_2}}\cdot \frac{1}{A_3}<{\left(\frac{1}{A_1+1}\right)}^2\frac{1}{A_3}\le \frac{1}{4}.\end{array}$

通过逐步递推的方式，我们可以得到

$X_{2n+1}\left(\omega \right)-X_{2n}\left(\omega \right)<{\left(\frac{1}{A_1+1}\right)}^2\cdots {\left(\frac{1}{A_{2n-1}+1}\right)}^2\frac{1}{A_{2n+1}}\le \frac{1}{4^n}\to 0,n\to \infty .$

综合前三步的结论，由区间套定理可知，前文定义的 $X\left(\omega \right)$ 是存在的，并且 $X_n\left(\omega \right)\stackrel{a.s.}{\to }X\left(\omega \right),n\to \infty$。

3. 独立同分布情形偏差下界的估计

该部分首先给出定理3的证明，然后对几种分布来给出下界估计的具体数值。

定理3的证明：由 $b=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}$ 可知，事件 $\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}$ 可写为 $\left\{\left|\frac{1}{n}\log Q_n-b\right|>\delta \right\}$，由于

$\left\{\left|\frac{1}{n}\log Q_n-b\right|>\delta \right\}=\left\{\frac{1}{n}\log Q_n-b>\delta \right\}\cup \left\{\frac{1}{n}\log Q_n-b<-\delta \right\},$

所以

$\left\{\left|\frac{1}{n}\log Q_n-b\right|>\delta \right\}\supset \left\{\frac{1}{n}\log Q_n-b>\delta \right\}=\left\{Q_n>{\text{e}}^{n\left(b+\delta \right)}\right\}.$

注意到 $Q_n=A_n{Q}_{n-1}+Q_{n-2},\forall n\in {\mathbb{N}}_{+}$，其中 $Q_{-1}=0,Q_0=1$，则 $Q_1=A_1\ge A_1>0,Q_2=A_2{A}_1+1\ge A_2{A}_1>0$，因此 $\forall n\in {\mathbb{N}}_{+},Q_n\ge A_n{Q}_{n-1}\ge A_n\cdots A_1$。所以

$\left\{Q_n>{\text{e}}^{n\left(b+\delta \right)}\right\}\supset \left\{A_n\cdots A_1>{\text{e}}^{n\left(b+\delta \right)}\right\}\supset \left\{A_n>{\text{e}}^{b+\delta }\right\}\cap \cdots \cap \left\{A_1>{\text{e}}^{b+\delta }\right\}.$

从而

$P\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}\ge P\left(\left\{A_n>{\text{e}}^{b+\delta }\right\}\cap \cdots \cap \left\{A_1>{\text{e}}^{b+\delta }\right\}\right).$

由于 $\left\{A_n|n\ge 1\right\}$ 是独立同分布的，所以

$\begin{array}{c}P\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}\ge P\left(\left\{A_n>{\text{e}}^{b+\delta }\right\}\right)\cdots P\left(\left\{A_1>{\text{e}}^{b+\delta }\right\}\right)\\ ={\left(P\left(\left\{A_1>{\text{e}}^{b+\delta }\right\}\right)\right)}^n={\left(1-F\left({\text{e}}^{b+\delta }\right)\right)}^n.\end{array}$

从而得到了定理中的结果。

下面我们给出一些例子说明下界估计具体的值。

例1：设 $P\left(A_i=k\right)=\frac{1}{k\left(k+1\right)},\forall i\in {\mathbb{N}}_{+}$。

记 $b=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}$，此时，

$1-F\left({\text{e}}^{b+\delta }\right)={\displaystyle {\sum }_{k>{\text{e}}^{b+\delta }}P\left(A_i=k\right)}={\displaystyle {\sum }_{k>{\text{e}}^{b+\delta }}\frac{1}{k\left(k+1\right)}}=\frac{1}{\left[{\text{e}}^{b+\delta }\right]+1}$

其中 $\left[x\right]$ 表示实数x的整数部分，故

$P\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}\ge {\left(\frac{1}{\left[{\text{e}}^{b+\delta }\right]+1}\right)}^n$

例2：(泊松分布)设 $P\left(A_i=k\right)=\frac{{\text{e}}^{-\lambda }}{1-{\text{e}}^{-\lambda }}\cdot \frac{{\lambda }^k}{k!},\forall i\in {\mathbb{N}}_{+}$，其中 $\lambda >0$ 为固定参数。

记 $b=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}$，此时，

$1-F\left({\text{e}}^{b+\delta }\right)={\displaystyle {\sum }_{k>{\text{e}}^{b+\delta }}P\left(A_i=k\right)}={\displaystyle {\sum }_{k>{\text{e}}^{b+\delta }}\frac{{\text{e}}^{-\lambda }}{1-{\text{e}}^{-\lambda }}\cdot \frac{{\lambda }^k}{k!}}\ge \frac{{\text{e}}^{-\lambda }}{1-{\text{e}}^{-\lambda }}\cdot \frac{{\lambda }^{\left[{\text{e}}^{(b+\delta )}\right]+1}}{\left(\left[{\text{e}}^{(b+\delta )}\right]+1\right)!}$

从而

$P\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}\ge {\left(\frac{{\text{e}}^{-\lambda }}{1-{\text{e}}^{-\lambda }}\cdot \frac{{\lambda }^{\left[{\text{e}}^{\left(b+\delta \right)}\right]+1}}{\left(\left[{\text{e}}^{\left(b+\delta \right)}\right]+1\right)!}\right)}^n$

例3：(几何分布)设 $P\left(A_i=k\right)=s^{k-1}\cdot r,\forall i\in {\mathbb{N}}_{+}$，其中 $r>0,s=1-r>0$ 均为固定参数。

记 $b=-{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}$，此时，

$1-F\left({\text{e}}^{b+\delta }\right)=\underset{k>{\text{e}}^{b+\delta }}{{\displaystyle \sum }}P\left(A_i=k\right)=\underset{k>{\text{e}}^{b+\delta }}{{\displaystyle \sum }}{s}^{k-1}\cdot r=\frac{r}{s\left(1-s\right)}{s}^{\left[{\text{e}}^{b+\delta }\right]+1}$

所以，

$P\left\{\left|\frac{1}{n}\log Q_n+{\displaystyle {\int }_{\text{Ω}}\log X\text{d}P}\right|>\delta \right\}\ge {\left(\frac{r}{s\left(1-s\right)}{s}^{\left[{\text{e}}^{b+\delta }\right]+1}\right)}^n.$

文章引用

谢胜寒. 随机连分数收敛因子的收敛性和大偏差估计
Convergence and Large Deviation Estimation of Random Continuous Fractional Convergence Factors[J]. 应用数学进展, 2020, 09(05): 765-771. https://doi.org/10.12677/AAM.2020.95091

参考文献