Advances in Applied Mathematics
Vol.
10
No.
07
(
2021
), Article ID:
44044
,
9
pages
10.12677/AAM.2021.107254
Hardy空间上m-复对称Toeplitz算子
崔璞玉,王焕然,冯琳颖
辽宁师范大学数学学院,辽宁 大连

收稿日期:2021年6月19日;录用日期:2021年7月11日;发布日期:2021年7月22日

摘要
本文分两部分刻画了Hardy空间上m-复对称的Toeplitz算子的符号特征:1) 以解析函数或者余解析函数为符号的Toeplitz算子的m-复对称性及其与正规性的关系;2) 以较一般函数为符号的Toeplitz算子的2-复对称性。
关键词
Hardy空间,Toeplitz算子,共轭算子,m-复对称

m-Complex Symmetric Toeplitz Operators on the Hardy Space
Puyu Cui, Huanran Wang, Linying Feng
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Jun. 19th, 2021; accepted: Jul. 11th, 2021; published: Jul. 22nd, 2021

ABSTRACT
In this paper, the symbolic characteristics of m-complex symmetric Toeplitz operators on Hardy space are described in two parts: 1) the m-complex symmetry of Toeplitz operators with analytic functions or coanalytic functions as signs and their relations with normality; 2) the 2-complex symmetries of Toeplitz operators with more general functions as symbols.
Keywords:Hardy Space, Toeplitz Operators, Conjugate Operator, m-Complex Symmetric

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,复对称算子引起了国内外一些算子理论方面专家学者的关注,取得了一些重要的结果。关于复对称的Toeplitz算子也有一些较好的结果 [1] [2] [3] [4]。韩国学者Ko和Lee将复对称算子的概念推广,提出了m-复对称算子的概念 [3]。特别的,1-复对称算子即为复对称算子。本文研究Hardy空间上Toeplitz算子的m-复对称性问题,刻画了分别以解析函数和余解析函数为符号的m-复对称Toeplitz算子的符号函数的函数特征,通过泊松变换等分析技巧对以较一般化函数为符号的2-复对称Toeplitz算子也给出了刻画。
2. 预备知识
本文以
表示复可分Hilbert空间,
表示
上所有有界线性算子的集合。记
是复平面
上的开单位圆盘,
为
上的单位圆周。记由
上所有关于弧长测度平方可积的函数构成的Banach空间为
。记由所有有界解析函数构成的空间为
。
定义1.1 由
中所有负幂项Fourier系数为零的平方可积的函数构成的闭子空间为Hardy空间,记为
。由于其等距同构于所有满足幂级数展开式的系数平方可和的解析函数构成的Hilbert空间,故有时也记为
表示
上本性有界可测函数空间。令
,称以
为符号的Toeplitz算子为
这里
表示
到
的正交投影。
Toeplitz算子具有如下性质:令
,,则
1)
。
2)
。
此外,若
是解析的,则
3)
。
4)
。
定理1.2 [5] Toeplitz算子
是正规的当且仅当存在
,实值函数
,使得
Hardy空间
的在点
的再生核可表示为
正规化为
若
且
在
解析,那么
。
定义1.3 若
上共轭线性算子
满足:
1)
对于所有的
。
2)
。
则称C为
上的共轭算子。
定义1.4 设
,若存在一个
上的共轭算子C,使得
,则称T是C-对称的。若T关于某个共轭算子C是C-对称的,则称T是复对称的。
定义1.5 设
,称Toeplitz算子
关于共轭算子C是
-复对称的,若满足
文献 [6] 中提出一类共轭算子
其中
,。
一般情况下,我们只需考虑特殊的共轭算子,见下面定理
定理1.6 [6] Hardy空间上的有界线性算子T关于共轭算子
是复对称的当且仅当T关于
复对称。
本文主要研究关于共轭算子
的m-复对称Toeplitz算子,其中
满足
这里
。易见,
是
上的共轭算子,且
。进一步
3. Hardy空间上以解析(余解析)函数为符号的m-复对称Toeplitz算子
本部分研究以解析函数或者余解析函数为符号的Toeplitz算子的m-复对称性,得到下面结论。
定理2.1 对于
, 为
上关于
的m-复对称算子,则下述成立
1) 若
是解析的,则
,(c为常数)。
2) 若
是余解析的,则
,(c为常数)。
证明:不失一般性,我们以
为例,即证
1) 充分性显然,下证必要性。
若
为3-复对称算子,由Toeplitz算子的基本代数性质得
取
,由
那么
因为
,所以
,即
。
2) 下证必要性。往证
。记
是
上的正规正交基
因而
对应的矩阵表示为
即为以解析函数
为符号的Toeplitz算子
的矩阵表示,进而
。
由Toeplitz算子的基本代数性质得
显然
令
,由于
在
上的径向极限存在,所以
其中
,进而
而
是关于
的解析函数,
是关于
的余解析函数,所以
。
推论2.2 若
,那么下述成立
1)
为
上关于共轭算子
的m-复对称算子
,当且仅当
是正规算子。
2) 若
, 为
上关于共轭算子
的m-复对称算子
,当且仅当
是正规算子。
证明:由定理2.1直接可得。
4. Hardy空间上2-复对称Toeplitz算子
本部分首先刻画解析符号和余解析符号的Toeplitz算子关于共轭算子
的2-复对称性。
若
,其中
。那么由Toeplitz算子基本性质有
进一步,
因此,
由再生核的定义,得到
由定义计算可得
同理可得
综合上面结果,若
为
上关于
的2-复对称算子,那么对于
,有
(3.1)
进一步,若(3.1)式中
,对(3.1)式两端求
得
运用多复变函数常见技巧,令
,有
(3.2)
记幂级数展开式为
,那么
在此基础上计算有
进一步求偏导数得
相同方法有
和
直接计算得
和
将上述所有结果带入(3.2)式且令
,得
对比两端
的系数,所以当
时,
整理得
(3.3)
当
时
(3.4)
综合以上结果得到
定理3.1 假设
,且
。
为
上关于
的2-复对称算子,那么
且
其中
。
如果对Toeplitz算子
的符号函数做一些限制,可以得出一些整齐的结果。
推论3.2 假设
,,,且
。
为
上关于
的2-复对称算子,那么
且
推论3.3 若
, 且
。如果
为
上关于
的2-复对称算子,那么
或
或
或
证明:令 。由定理3.1,结合前面(3.3)和(3.4)式有
。由定理3.1,结合前面(3.3)和(3.4)式有
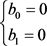 或
或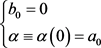 或
或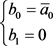 或
或
当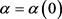 时,
时, 为解析Toeplitz算子,再运用定理2.1,
为解析Toeplitz算子,再运用定理2.1, ,(c为常数)。因此
,(c为常数)。因此
 或
或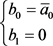 或
或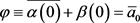 或
或
如果对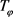 的符号函数做进一步限制,得到下面一个有意思的结果。
的符号函数做进一步限制,得到下面一个有意思的结果。
定理3.4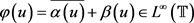 ,
, 且
且 。如果
。如果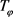 为
为 上关于
上关于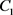 的2-复对称算子,那么
的2-复对称算子,那么 ,(c为常数)。
,(c为常数)。
证明:由推论3.2,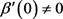 ,那么推论的结果,只能是第三种或第四种情况。无论哪一种情况,都得到
,那么推论的结果,只能是第三种或第四种情况。无论哪一种情况,都得到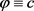 ,(c为常数)。
,(c为常数)。
文章引用
崔璞玉,王焕然,冯琳颖. Hardy空间上m-复对称Toeplitz算子
m-Complex Symmetric Toeplitz Operators on the Hardy Space[J]. 应用数学进展, 2021, 10(07): 2419-2427. https://doi.org/10.12677/AAM.2021.107254
参考文献
- 1. Garcia, S.R. and Putinar, M. (2006) Complex Symmetric Operators and Applications. Transactions of the American Mathematical Society, 358, 1285-1315. https://doi.org/10.1090/S0002-9947-05-03742-6
- 2. Guo, K. and Zhu, S. (2014) A Canonical Decomposition of Complex Symmetric Operators. Operator Theory, 72, 529-547. https://doi.org/10.7900/jot.2013aug15.2007
- 3. Ko, E. and Lee, J. (2016) On Complex Symmetric Toeplitz Operators. Journal of Mathematical Analysis and Applications, 434, 20-34. https://doi.org/10.1016/j.jmaa.2015.09.004
- 4. Li, R., Yang, Y. and Lu, Y. (2020) A Class of Complex Symmetric Toeplitz Operators on the Hardy and Bergman Spaces. Journal of Mathematical Analysis and Applications, 489, 124173. https://doi.org/10.1016/j.jmaa.2020.124173
- 5. Martinez-Avendano, R.A. and Rosenthal, P. (2007) An Introduction to Operators on the Hardy-Hilbert Space. Graduate Texts in Mathematics, 237, Springer-Verlag, New York.
- 6. Kang, D.O., Ko, E. and Lee, J.E. (2019) On Complex Symmetric Block Toeplitz Operators. arXiv: 1904. 04410[math. FA].







 。由定理3.1,结合前面(3.3)和(3.4)式有
。由定理3.1,结合前面(3.3)和(3.4)式有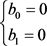 或
或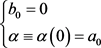 或
或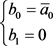 或
或
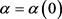 时,
时, 为解析Toeplitz算子,再运用定理2.1,
为解析Toeplitz算子,再运用定理2.1, ,(c为常数)。因此
,(c为常数)。因此 或
或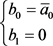 或
或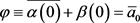 或
或
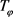 的符号函数做进一步限制,得到下面一个有意思的结果。
的符号函数做进一步限制,得到下面一个有意思的结果。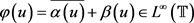 ,
, 且
且 。如果
。如果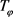 为
为 上关于
上关于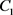 的2-复对称算子,那么
的2-复对称算子,那么 ,(c为常数)。
,(c为常数)。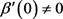 ,那么推论的结果,只能是第三种或第四种情况。无论哪一种情况,都得到
,那么推论的结果,只能是第三种或第四种情况。无论哪一种情况,都得到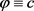 ,(c为常数)。
,(c为常数)。