Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30349
,
7
pages
10.12677/PM.2019.93051
The Inverse Question of the Equal Segmentation Problem of Squares
Youning Wang, Xiaole Su
Laboratory of Mathematics and Complex Systems of Ministry of Education, School of Mathematical Science, Beijing Normal University, Beijing

Received: Apr. 26th, 2019; accepted: May 6th, 2019; published: May 22nd, 2019

ABSTRACT
In this paper, we focus on the inverse question of the equal segmentation problem of squares and obtain some interesting results.
Keywords:Regular Polygon, Equal Segmentation Problem, Square
正方形等截分之逆问题
王幼宁,苏效乐
北京师范大学数学科学学院,数学与复杂系统教育部重点实验室,北京

收稿日期:2019年4月26日;录用日期:2019年5月6日;发布日期:2019年5月22日

摘 要
本文讨论了正方形等截分问题的逆问题,得到不同情况下一些有意思的结果。
关键词 :正多边形,等截分,正方形

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
所谓正多边形等截分问题是指:在正n边形的n条边上顺序截取等长线段得到n个截点,它们一定能顺序成为某个正n边形的n个顶点。其求解并不复杂,但其逆问题的求解 [1] [2] [3] 却不是那么显然的。本文将合理利用解析几何的方法,讨论n = 4的情形,也就是正方形的等截分问题的逆问题并给出解析研讨。
事实上,不仅可以考虑等长截点落在原四边形各边之上,还可以考虑截点落在各边的有向延长线上。于是推广了的正方形等截分点相应性质依然具备,同时逆问题可以相应推广。寻找该逆问题的初等几何解法是不容易的;本文的主要结果将给出其解析解法,自然推广原有结果。
本文总考虑顺序以点A1,A2,A3,A4为顶点的正定向四边形A1A2A3A4。记顶点Ai到Ai+1的边长为ai > 0,顶点Ai之处的(有向)内角为
,以有向截长
在边AiAi+1或其延长线上从Ai出发所截得之点为Pi,其中记
,
,
,
。熟知有四边形(不一定凸)内角和
. (1)
2. 准备工作
先给出一个四边形等截分问题的一个等价条件。
引理1上述正定向四边形A1A2A3A4的以有向截长
确定的等截分点四边形P1P2P3P4恰好成为正方形的充要条件是其边长、内角以及等截长满足(1)式以及
,(2)
, (3)
其中
。并且,在指标4阶循环意义下的任意指定的2个相邻i所对应的(2)和(3)式中两对方程,蕴含于整个方程组的其余两对方程之中。
证明等截分点四边形P1P2P3P4是正方形的充要条件是其4个边向量PiPi+1,
循序旋转p/2相等,或者等价地说,相邻两边垂直且相等。
由于正方形的各组相邻边的关系是相同的,故只需要首先分别考虑Pi-1Pi和PiPi+1成为某个正方形的一组相邻边的充要条件。
为此,以Ai为原点、以向量AiAi+1为水平轴正向向量建立符合定向的直角坐标系,如图1所示,则相关各点坐标可分别确定为
,
,
,
,
,
。此时,四边形P1P2P3P4的边向量
,
.
同时,这两条边向量旋转p/2相等的条件在此坐标系下看成复向量(也可以用矩阵)的表达形式即为
, (4)
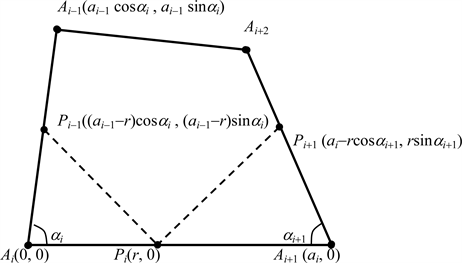
Figure 1. Sketch map of equal segmentation
图1. 等截分示意图
其中
为虚数单位。分量形式即分别为
,
.
它们分别对应于(2)和(3)式中指标i相同的一对方程。
注意到(2)和(3)式之中的几何量与坐标系选取无关,故与(1)式联立时等价于等截分点四边形P1P2P3P4的4个边向量PiPi+1,
循序旋转p/2是相等的,从而是它成为正方形的充要条件。进一步,注意到在指标循环意义下的两对相邻边向量循序旋转p/2相等,则蕴涵着另外两对也同时成立,其中内角取值满足(1)式,因而结论成立。
引理2上述正定向四边形A1A2A3A4若具有以两种有向截长r1,r2 (r1 ¹ r2)所分别确定的等截分点四边形分别为正方形,则A1A2A3A4必为正方形,从而其对于任意截长所得到的等截分点四边形均为正方形。
证明对于给定的正定向四边形A1A2A3A4,若以有向截长r1 ¹ r2所分别确定的等截分点四边形分别为正方形,则由引理1结论,(2)和(3)式对于r = r1和r = r2都成立,重写为r的一次方程组
,
.
注意到各边长ai > 0,得到
,
,
,
,
其中
。注意到
,
,该组条件意味着只能有
,
,
.
即得A1A2A3A4为正方形。
引理3 上述正定向四边形A
1 A
2 A
3 A
4若仅具有唯一的有向截长
使得所确定的等截分点四边形P1P2P3P4恰好为正方形,则在(1)式联立(2)式、(3)式所得到的方程组之中,(3)式等价于方程
, (5)
而(2)式当
时可以等价置换为方程
, (6)
其中
。
证明现在A
1 A
2 A
3 A
4不是正方形,否则由引理2可知矛盾。由引理1证明过程可知,(2)式对应等价于
, (7)
其中
。同时(3)式显然等价于(5)式,并且可以按指标组等价改写为
. (8)
现在,(7)、(3)、(8)式所对应3元线性方程组有非零解
的充要条件是其系数矩阵的行列式为零,即有
此即按指标组等价于(6)式。注意到当
时(6)式意味着(7)式可由方程(3)和(8)式线性表出,故此时(2)式可以等价置换为方程(6)式,结论得证。
引理4 上述正定向四边形A
1 A
2 A
3 A
4若是凸的并且仅具有唯一的有向截长
使得所确定的等截分点四边形P1P2P3P4恰好为正方形,则
时,(1)式联立(2)式、(3)式所得到的方程组等价于(1)式联立(5)、(6)式所得到的方程组。
证明 现在A
1 A
2 A
3 A
4具有正定向且凸,意味着
,
。由引理2可知它不是正方形,由引理3可知现只需证明
,
。
用反证法,不妨设
使
,则
,此时(2)、(3)式对应于指标i分别取为j和j + 1而化简得到两组等式
,
,
,
.
进而,由第二组式子可知,
,
.
于是可递推得到A1A2A3A4各内角相同、各边等长,与它不是正方形矛盾。结论得证。
引理5 对于给定的不是正方形的正定向四边形A1A2A3A4,若存在一致小于(或一致大于)各边之长的有向截长
使其所确定的等截分点四边形P1P2P3P4恰好为正方形,则A
1 A
2 A
3 A
4的内角不能有取值p/2的。
证明 若
使某个内角
,则(2)式和(3)式变为
,
,
现在
或
,可得
,
.
注意到凸性意味着
,可得唯一解
。关于指标j递推归纳则得4个内角都等于p/2,再回到(2)式得到各边长也都相等,与A
1 A
2 A
3 A
4不是正方形矛盾。得证。
3. 主要结果
有了前述的准备工作,本节给出本文的几个主要结果。
定理1 对于给定的正定向凸四边形A
1 A
2 A
3 A
4,若存在使截点都落在各边之上的有向截长
所确定的等截分点四边形P1P2P3P4恰好为正方形,则A
1 A
2 A
3 A
4必为正方形。
证明 四边形A
1 A
2 A
3 A
4是凸的,即有
,
;而截点都取在各边之上,即
,则由(3)式知道
,
。进而在(1)式限制下只能有
,
。从而再由(2)式得知
,
。故由引理1可得A
1 A
2 A
3 A
4必为正方形。
这说明对于凸四边形来说,截点都落在各边内部时,只有正方形本身的等截分四边形是正方形.
进一步,当不要求满足凸性或截点可以取在某条边的延长线之上时,联立(1)式、(2)式和(3)式所得到的方程组都具有不是正方形的相应特定解。
引理6 对于给定的不是正方形的正定向四边形A
1 A
2 A
3 A
4,若存在有向截长
所确定的等截分点四边形P1P2P3P4恰好为正方形,则A
1 A
2 A
3 A
4的内角不能有取值±p/2。
证明 若
使某个内角
,则由(3)式得
为直角,关于指标递推则得4个内角都等于直角,再回到(2)式得到各边长也都相等,与A
1 A
2 A
3 A
4不是正方形矛盾。
而若
使
,由(3)式则得
,回到上一情形,矛盾。
综合以上两种情况命题得证。
定理2 对于给定的不是正方形的正定向四边形A
1 A
2 A
3 A
4,其仅具有唯一的有向截长
使得所确定的等截分点四边形P1P2P3P4恰好为正方形的充要条件是其边长、内角以及等截长满足(1)式以及方程组
, (9)
, (10)
其中
。此种情形下,(9)式所代表的4个方程之中,任意指定的2个相邻指标i所对应的2个方程都在(1)式约束下等价于另外2个方程。
证明 注意到引理1、引理2、引理3、引理6,此时4个内角都不等于正负直角,(5)式和(6)式分别等价于(10)式和(9)式,得证。
定理2给出了不是正方形的四边形等截分得到正方形的充要条件。而且,进一步,实际上等截分得到正方形的解有无穷多个,比如四边形中有一组对边相互平行时,就有下面的结果:
定理3 对于给定的正定向梯形(本文梯形仅指有一组对边平行,也就是包含平行四边形的情况) A
1 A
2 A
3 A
4,若存在有向截长
所确定的等截分点四边形P1P2P3P4恰好为正方形,则A
1 A
2 A
3 A
4必为平行四边形;并且当它不是正方形时,其各边长与等截长的比值由其锐内角唯一确定,对应通解在全等意义下诸如
,
,
. (11)
证明 由梯形条件可知,不妨假设
,其中
,i = 1, 2, 3, 4。注意到引理1、引理2、引理6和定理2,现在只需要在A
1 A
2 A
3 A
4不是正方形的情形之下,考虑联立(1)式、(9)式和(10)式的通解。此时(9)式当取i = 2时即可简化为
,
从而分以下两种情形:
情形一,
,进一步
,于是A
1 A
2 A
3 A
4是平行四边形,此时(9)式当取i = 4时的方程与取i = 2时的等价,当取i = 3时的方程与取i = 1时的等价且自然满足,即已得联立(1)式和(9)式的通解。再由(10)式即得a
1 = a
3,a
2 = a
4,且
, (12)
, (13)
在全等意义下不妨取锐内角为a1,则通解即如(11)式。
情形二,
,进一步
,于是A
1 A
2 A
3 A
4是等腰梯形,此时(9)式当取i = 4时的方程与取i = 2时的等价,当取i = 3时的方程与取i = 1时的等价且简化为
,
,
在所讨论的范围内无解。
故综合两种情形得知结论成立。
注记1 对于定理3之中的平行四边形通解,将(12),(13)两式分别相除和相加,有
,
.
特别当a1可尺规作出时,比如等于p/4时,对应图形可尺规做出。同时,极限情形有
,
.
注记2 对于其它四边形,也可以用画图软件说明有很多四边形等截分都能得到正方形。但相关分类并不简单,后续可以继续研究。
对于一般的多边形边数大于4的情形,讨论所论逆问题解的分类问题也是有意义的,但预期是复杂的,有待于进一步研究。
基金项目
本项研究受到国家自然科学基金资助,项目号11471039。
文章引用
王幼宁,苏效乐. 正方形等截分之逆问题
The Inverse Question of the Equal Segmentation Problem of Squares[J]. 理论数学, 2019, 09(03): 386-392. https://doi.org/10.12677/PM.2019.93051
参考文献
- 1. 张慧欣. 一个几何问题的思考[J]. 数学通报, 2012, 51(11): 53-54.
- 2. 张新. 对正三角形等截分逆问题的再思考[J]. 数学通报, 2015, 54(5): 59-60.
- 3. 王幼宁. 正三角形等截分逆问题的推广及其解析求解[J]. 数学通报, 2016, 55(5): 51-53.







