Pure Mathematics
Vol.
13
No.
05
(
2023
), Article ID:
66340
,
11
pages
10.12677/PM.2023.135140
基于分解的约束多目标进化算法
张鹏懿
广东工业大学数学与统计学院,广东 广州
收稿日期:2023年4月21日;录用日期:2023年5月23日;发布日期:2023年5月30日

摘要
现实世界中为平衡多方利益,需要进行多目标优化的研究,然而实际问题中多数问题往往带有约束条件,富有挑战性。在研究中,首要解决的问题为如何处理在优化过程中出现的非可行解。我们认为非可行解在优化过程中是重要的,其包含着种群进化方向的信息,需在优化过程中保存适当比例的非可行解。为此本文提出了一种基于分解的约束多目标进化算法,根据进化过程中种群变化来自适应产生权重保留一部分非可行解引导种群收敛。为验证所提算法的性能,选取了24个测试问题,4个对比算法,经数值实验证明了所提算法的有效性。
关键词
约束多目标,进化算法,基于分解的,自适应权重

Decomposition-Based Constrained Multi-Objective Evolutionary Algorithm
Pengyi Zhang
School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou Guangdong
Received: Apr. 21st, 2023; accepted: May 23rd, 2023; published: May 30th, 2023

ABSTRACT
In the real world, it is necessary to study multi-objective optimization in order to balance multi-interests. However, most of the practical problems are often challenging with constraints. How to deal with the infeasible solution in the optimization is the most important problem to be solved in the research. We think that the infeasible solution is important in optimization, and it contains the information of population evolution direction, so it is necessary to keep an appropriate proportion of the infeasible solution in optimization. In this paper, a decomposition-based constrained multi-objective evolutionary algorithm is proposed, which adaptively generates weights according to population changes in evolution and preserves some infeasible solutions to guide population convergence. In order to verify the performance of the proposed algorithm, 24 test problems and 4 comparison algorithms are selected. Numerical experiments show the effectiveness of the proposed algorithm.
Keywords:Constrained Multi-Objective, Evolutionary Algorithm, Decomposition-Based, Adaptive Weight

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着科技进步和社会发展,越来越多的问题需要在多个目标之间进行权衡取舍。例如,在工业领域中,我们常常需要考虑成本、质量和生产效率等多个指标,而在城市规划中,则需要平衡经济发展、环境保护和社会公正等多个方面的利益。在这种情况下,传统的单目标优化方法往往无法满足我们的需求。为了解决这个问题,研究者们开始转向多目标优化方法,并将其应用于各种实际问题中。然而,在实际问题中,多目标优化往往受到各种约束条件的限制。
在过去几十年里,研究者们提出了许多不同的约束多目标优化算法 [1] 。K. Deb.提出了CDP (Constrained Dominance Principle)约束处理技术 [2] ,因其简单有效的处理约束,成为现今适用范围最广泛的约束处理技术,Peng [3] 等人将约束违反程度作为一个新的目标,设计了一种新的基于有向权重的CHT来求解CMOP,其中使用分别分布在可行和可行区域中的两种类型的权重来引导搜索到有希望的区域。Tian等人 [4] 提出了一种求解CMOP的共同进化框架(CCMO),其中一个种群用来求解原始的CMOP,即搜索CPF (constrained Pareto front),而另一个种群忽略约束来寻找UPF (unconstrained Pareto front)。此外,这两个群体相互协助求解CMOP。Fan [5] 等人提出了PPS (Push and pull search)框架。在push阶段的目标是引导种群穿过不可行区域到达UPF。在pull阶段,采用改进的ε约束方法来指导种群搜寻CPF。基于PPS框架,将CMOP分解为一组简单的子问题,每个子问题对应一个子种群,并将PPS框架应用于每个子种群以解决相关的子问题。
然而由于约束条件的存在,其求解难度相较于无约束优化问题大幅增加。现存约束多目标进化算法,大多针对某一类问题表现较好,缺乏一种鲁棒性更强的约束多目标优化算法,这是目前亟需解决的问题。
2. 预备知识
2.1. 约束多目标优化模型
不失一般性,由m个目标函数,n维决策变量以及若干约束组成的约束多目标优化问题,其数学模型表达如下:
(1)
其中 为n维决策变量,决策变量x的取值范围由:
(2)
(3)
共同决定,称为决策空间。
另外, 定义了p个不等式约束条件, 定义了 个等式约束条件。对每一个决策变量x,其对第j个约束条件的约束违反程度(constraint violation degree)定义为:
(4)
其中 通常为一个非常小的正数。通过对每一个约束条件的约束违反程度相加,可得其总的约束违反程度为:
(5)
如果一个决策变量的CV值是0,那么则可以说明此解为可行解,反之此解为非可行解。
若有两个可行解x1和x2,对任一 都有 且存在至少一个 有 ,则称x1支配x2。如果一个解x不被其他任何解支配,则称此解为问题(1)的Pareto最优解,所有Pareto最优解的集合构成PS (Pareto optimal solutions),对应至目标空间为Pareto前沿PF (Pareto front)。
2.2. MOEA/D-M2M算法模型
MOEA/D-M2M [6] 是一个基于分解的多目标优化算法,具有较强的维持种群多样化的能力,求得的解分布性较为均匀。其中心思想为将问题分解为若干个子问题来同事解决和优化。具体为在目标空间中产生K个单位中心权重向量 ,将目标空间分为K个子区域 , 为:
(6)
其中 为目标向量与中心权重向量 的角度。基于此类分区,问题(1)可转化为:
(7)
3. 算法设计
3.1. 多目标优化方法
单目标约束优化问题中,常使用将约束违反程度CV记为另外一个目标函数,将其转化为一个无约束的双目标优化问题的方法求解。那么借鉴此思路,在m维约束多目标优化问题当中,可将约束违反程度CV,记为第 个目标函数,由此可将问题(1)转化为:
(8)
Peng等人根据此方法设计了一种基于动态权重的约束多目标优化算法 [3] ,其通过不断调整不可行权重与可行超平面角度,实现在种群进化过程中向可行超平面收敛。但是由于此种权重调整策略默认随着种群的进化,个体违反约束程度呈正相关降低,导致其容易在接近PF处出现连续不可行区域中陷入局部最优。本文考虑引入自适应权重产生策略,根据种群中可行解比例调整可行与不可行权重数量,着重保留有希望的不可行解,引导种群跳出局部最优。
3.2. 权重产生策略
Table 1. Weight generation strategy
表1. 权重产生策略
首先引入预期可行解比例 ,实际可行解比例 。其中 为种群进化至第t代时期望达到的可行解所占比例, 为第t代时可行解占实际种群的比例。
不同于 [3] 产生固定的可行与不可行权重数量,此权重产生策略将动态调整可行与不可行权重的数量。为确保进化方向是收敛的,那么就要求可行权重所占比例要与进化代数t呈正相关性,否则算法无法收敛。权重产生策略如表1所示,其中 为在可行超平面中均匀产生的单位可行权重向量。
3.3. Adaptive Weight算法
AW (Adaptive weight)算法框架基于MOEA/D-M2M [6] ,其算法框架图如表2所示:
Table 2. AW algorithm framework
表2. AW算法框架
Step 3中选用DE/rand/1/bin [7] 算子产生后代
Step 6中对于任一给定的m+1维权重向量 ,每一个解都可通过以下:
(9)
公式计算出ASF [8] 数值。其中 为参考点, 表示当前种群中所出现的 最小值。
存档集A用以存放种群进化过程中产生的可行解。若存档集A中数量少于等于N,则直接更新存档集A,否则将通过(9)式选取N个具有较好收敛性和散布性的可行解来更新存档集A。
4. 数值实验
4.1. 参数设置
参数的设定与调整对于算法的运行是有较大影响的,因此,对算法进行合理的参数设置是十分有必要的。经过数值分析拟将若干参数设定为:种群数量 ,分区数 ,权重数量 = 100,最大评估次数 ,最大进化代数 ,DE算子中 、 。另外对于预期可行解比例定义如下:
(10)
4.2. 测试问题集
本实验中选用C_DTLZ系列 [9] 以及MW系列 [10] 测试集。
通过对比无约束优化问题UPF (unconstrained Pareto front)和带约束优化问题CPF (constrained Pareto front),可发现两类PF并不完全相同,大致可分为以下四种情况如图1所示:
Type I: CPF与UPF完全相同;
Type II: CPF完全是UPF的一部分;
Type III: CPF一部分与UPF相同;
Type IV: CPF与UPF完全不同。
根据上述条件,可将两类测试集中的问题进行分类,如表3所示:
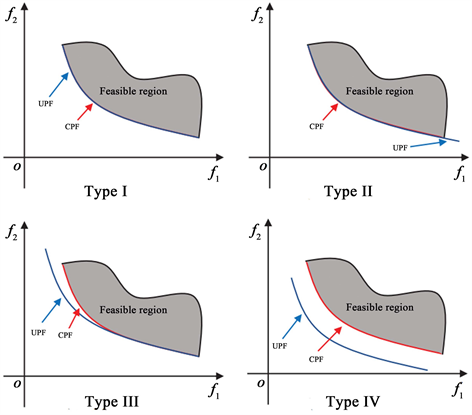
Figure 1. Classification of CPF and UPF
图1. CPF与UPF分类
Table 3. CPF classification of test problems
表3. 测试问题CPF分类
4.3. 性能指标
4.3.1. IGD指标
IGD指标 [11] 评估的是从真实Pareto最优集中的点到实际求得的非劣解集合的平均欧氏距离。它用一组足够多的点来衡量种群的收敛性与散布性。一般来讲IGD值越小,所得到的种群最接近PF,且具有更好的散布性。给定 为均匀散布在PF上的点的集合,P为算法所求得的最优解集所包含的点,那么IGD公式可定义为:
(11)
4.3.2. HV指标
HV指标 [12] 评估的是算法实际求得的非劣解集合中的解与参考点之间形成空间的超体积,同样能够同时衡量种群的收敛性与散布性。一般来讲HV值越大,所得到的种群则更接近PF,且具有更好的散布性。给定参考点Z,X为算法实际所求得的非劣解集,x为X中的个体,那么HV公式可定义为:
(12)
由于HV指标在计算过程中并未使用真实PF数据,所以其可适用于一些PF未知问题的算法性能检验当中,而IGD指标则无法做到。
4.4. 实验结果
本次试验中,我们使用了DW [3] 、CCMO [4] 、PPS [5] 、IDBEA [13] 作为AW的对比算法,并给出了对应的对比实验结果。因与DW拥有较为类似的算法机制,所以须重点关注权重产生策略不同之处所带来的算法性能的影响。为尽可能消除偶然误差,每个算法将在Platemo [14] 平台上对测试问题运行30轮,并取IGD、HV结果平均值。
Table 4. The algorithm runs average IGD results in 30 rounds of test problems
表4. 算法在测试问题30轮运行平均IGD结果
Table 5. The algorithm runs average HV results in 30 rounds of test problems
表5. 算法在测试问题30轮运行平均HV结果
表4、表5可以看出与DW相比,AW算法几乎在任何测试问题上的表现都要更好;与其他算法相比较,在MW14、MW6、MW8、DC1_DTLZ3、MW10、MW13、MW9中AW的性能也有明显的优势。尤其以MW10、MW8最为显著。

Figure 2. Optimal solutions of each algorithm in two-dimensional problem MW10
图2. 各算法在二维问题MW10中所求的最优解
从图2可以看出在二维测试问题MW10中可以看出AW算法最终求得的非劣解相较于对比算法展现出更好的收敛性和散布性。由于AW算前期产生了较多不可行权重,保留了较多有希望的不可行解帮助算法在进化前期阶段快速跳出局部可行域,更快进入PF可行域中,有效的提升算法的收敛性能。同时由于采用M2M [6] 框架权重在各个子区域中均匀产生,种群进化过程中保留了更多分布均匀的解,有效提升了各个阶段种群的散布性。
从图3可以看出在三维测试问题MW8中AW算法相较于其他对比算法也具有更佳的收敛性。由于在自适应权重产生策略,在种群进化后期可行权重数量增加引导种群向PF收敛,相较于DW [3] 的固定可行权重数量可展现出更好的收敛性能。

Figure 3. Optimal solutions of each algorithm in three-dimensional problem MW8
图3. 各算法在三维问题MW8中所求的最优解
5. 总结
在本文中,我们提出了不同的权重产生策略以处理多目标约束优化问题,并将此整合为新的命名为AW算法。在数值实验中,AW算法在测试问题中展现出了较好的性能,说明了算法的有效性和适应性。
未来的工作中,可能会继续针对权重产生策略、参数敏感性分析等进行改进,并将其应用拓展至更高维度问题中。
文章引用
张鹏懿. 基于分解的约束多目标进化算法
Decomposition-Based Constrained Multi-Objective Evolutionary Algorithm[J]. 理论数学, 2023, 13(05): 1370-1380. https://doi.org/10.12677/PM.2023.135140
参考文献
- 1. Liang, J., et al. (2023) A Survey on Evolutionary Constrained Multiobjective Optimization. IEEE Transactions on Evolu-tionary Computation, 27, 201-221. https://doi.org/10.1109/TEVC.2022.3155533
- 2. Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T. (2002) A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182-197. https://doi.org/10.1109/4235.996017
- 3. Peng, C., Liu, H.-L. and Gu, F. (2017) An Evolutionary Algorithm with Directed Weights for Constrained Multi-Objective Optimization. Applied Soft Computing, 60, 613-622. https://doi.org/10.1016/j.asoc.2017.06.053
- 4. Tian, Y., Zhang, T., Xiao, J., Zhang, X. and Jin, Y. (2020) A Coevolutionary Framework for Constrained Multi-Objective Optimization Problems. IEEE Transactions on Evolutionary Computation, 25, 102-116. https://doi.org/10.1109/TEVC.2020.3004012
- 5. Fan, Z., Li, W., Cai, X., Li, H., Wei, C., Zhang, Q., Deb, K. and Goodman, E.D. (2017) Push and Pull Search for Solving Constrained Multi-Objective Optimization Problems. Swarm and Evolutionary Computation, 44, 665-679. https://doi.org/10.1016/j.swevo.2018.08.017
- 6. Liu, H., Gu, F. and Zhang, Q. (2014) Decomposition of a Multiobjective Optimization Problem into a Number of Simple Multiobjective Subproblems. IEEE Transactions on Evolutionary Computation, 18, 450-455. https://doi.org/10.1109/TEVC.2013.2281533
- 7. Jia, G., Wang, Y., Cai, Z. and Jin, Y. (2013) An Improved (μ+ λ)-Constrained Differential Evolution for Constrained Optimization. Information Sciences, 222, 302-322. https://doi.org/10.1016/j.ins.2012.01.017
- 8. Wierzbicki, A.P. (1980) The Use of Reference Objectives in Multiobjective Optimization. Multiple Criteria Decision Making Theory and Application: Proceedings of the Third Conference Hagen/Königswinter, West Germany, 20-24 August 1979, 468-486. https://doi.org/10.1007/978-3-642-48782-8_32
- 9. Jain, H. and Deb, K. (2014) An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Non-Dominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Transactions on Evolutionary Computation, 18, 602-622. https://doi.org/10.1109/TEVC.2013.2281534
- 10. Ma, Z. and Wang, Y. (2019) Evolutionary Constrained Multiobjective Optimization: Test Suite Construction and Performance Comparisons. IEEE Transactions on Evolutionary Computation, 23, 972-986. https://doi.org/10.1109/TEVC.2019.2896967
- 11. Zhang, Q., Zhou, A. and Jin, Y. (2008) Rm-meda: A Regularity Model-Based Multiobjective Estimation of Distribution Algorithm. IEEE Transactions on Evolutionary Computation, 12, 41-63. https://doi.org/10.1109/TEVC.2007.894202
- 12. Zitzler, E. and Thiele, L. (1998) Multiobjective Optimization Using Evolutionary Algorithms: A Comparative Case Study. Parallel Problem Solving from Nature, PPSN V: 5th In-ternational Conference, Amsterdam, 27-30 September 1998, 292-301. https://doi.org/10.1007/BFb0056872
- 13. Asafuddoula, M., Ray, T. and Sarker, R. (2015) A Decomposi-tion-Based Evolutionary Algorithm for Many Objective Optimization. IEEE Transactions on Evolutionary Computation, 19, 445-460. https://doi.org/10.1109/TEVC.2014.2339823
- 14. Tian, Y., Cheng, R., Zhang, X.Y. and Jin, Y.C. (2017) PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization. IEEE Computational Intelligence Magazine, 12, 73-87. https://doi.org/10.1109/MCI.2017.2742868
