Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18461,11
pages
10.12677/AAM.2016.53060
E-Henig Proper Efficient Solution for Set-Valued Optimization Problems
Peijing Lin1, Maowang Li2, Qiusheng Qiu1
1Zhejiang Normal University, Jinhua Zhejiang
2Jiangxi Metallurgical Vocational and Technical College, Xinyu Jiangxi

Received: Aug. 9th, 2016; accepted: Aug. 24th, 2016; published: Aug. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study E-Henig proper efficient solution for set-valued optimization problem. Firstly, the concept of E-Henig proper efficient point in a real Hausdorff locally convex space is given. The relationships with E-Benson proper point and E-super point are discussed. Secondly, under the assumption of nearly subconvexlikeness, scalarization theorems of E-Henig proper efficient solution are established. Lastly, E-Henig saddle point theorem and E-Henig duality theorem are studied.
Keywords:E-Henig Proper Efficient Solution, Scalarization, Proper Saddle Point, Duality

集值优化问题的E-Henig真有效解
林佩静1,李茂旺2,仇秋生1
1浙江师范大学,浙江 金华
2江西冶金职业技术学院,江西 新余

收稿日期:2016年8月9日;录用日期:2016年8月24日;发布日期:2016年8月31日

摘 要
本文研究集值优化问题的E-Henig真有效解。首先,在实局部凸Hausdoff空间中引进了E-Henig真有效点的概念,给出了E-Henig真有效点的等价刻画,讨论了它与E-Benson真有效点和E-超有效点的关系。其次,在集值映射为近似E-次类凸的条件下,建立了E-Henig真有效解的标量化定理。最后,研究了E-Henig真有效解的鞍点定理和对偶定理。
关键词 :E-Henig真有效解,标量化,真鞍点,对偶

1. 引言
集值优化理论是最优化理论和应用的主要研究内容之一。它被广泛应用于经济均衡和军事决策等领域。由于存在多种不同形式的真有效解和近似真有效解的概念,因此如何提出统一的集值优化问题真有效解的概念,并在统一的框架下研究真有效解的标量化,鞍点以及对偶是十分重要的课题。目前,关于集值优化问题有效解和弱有效解的统一性研究比较多,如:2006年,Gutierrez等 [1] ,通过引进co-radiant集的概念定义了一类新的ε-有效解,并研究了它的线性与非线性标量化特征,这类新的近似有效解推广和统一了文献 [2] [3] 中的几种近似解的概念。2011年,Chicco在有限维空间中提出改善集的概念 [4] ,同时研究了其性质和几何意义。基于改善集,Gutierrez提出向量优化问题中的一类新的有效解的概念:E-有效解 [5] 。它统一了优化问题中的许多解的概念,如:数值优化问题的最优解和近似解,向量优化问题的(弱)有效解和近似(弱)有效解。2012年,赵克全等在Hausdoff局部凸空间中 [6] ,利用改善集的知识提出近似E-次类凸集值映射,建立相应的择一定理,并获得E-有效解的标量化定理,E-鞍点定理和E-对偶定理。2013年,赵克全和杨新民提出E-Benson真有效解的概念 [7] ,这类有效解推广了经典的Benson真有效解和ε-真有效解的概念。2016年,周志昂等提出了E-超有效解的概念 [8] ,获得标量化定理等结果。众所周知,对超有效点而言,它的存在性条件是非常强的,哪怕是紧凸集的条件下,也不能够保证它的存在性。另一方面,为讨论E-Benson真有效解的标量化问题,一般都要求序锥具有紧或弱紧基底(见 [7] )。在许多情况下,这些条件难以满足。而Henig真有效解既保持了超有效解的主要特征,同时它仅要求序锥具有基底。因此,研究Henig真有效解是有意义的。
本文在文献 [5] - [8] 的基础上,首先提出E-Henig真有效点的概念,它统一了Henig真有效点和ε-Henig真有效点等概念,随后给出了E-Henig真有效点的等价刻画以及存在性定理,并讨论了它与E-Benson真有效点和E-超有效点之间的关系。其次,在集值映射为近似E-次类凸的假设下,进一步研究了集值优化问题E-Henig真有效解的标量化定理。最后,提出E-Henig真有效解的鞍点和对偶的定义,同时得出鞍点定理及对偶定理。
2. 定义与引理
若无特别申明,以下总假设X是线性空间,Y和Z分别为实局部凸Hausdorff空间,Y*为Y的共轭空间, ,用
,用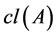 ,
, (或
(或 ),
),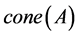 分别表示A的闭包,内部和生成锥。
分别表示A的闭包,内部和生成锥。
设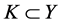 ,
, 为内部非空的闭凸点锥,由K诱导出Y的偏序,即
为内部非空的闭凸点锥,由K诱导出Y的偏序,即
 。
。
非空凸子集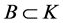 ,如果满足下列两个条件:
,如果满足下列两个条件:
1) 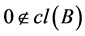
2)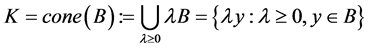 ,则称B为K的基底。
,则称B为K的基底。
如果基底B为有界(紧,弱紧)集,则称K具有有界(紧,弱紧)基底。
记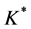 和
和 分别为K的对偶锥和所有严格正泛函,即
分别为K的对偶锥和所有严格正泛函,即
 。
。
设B为凸锥K的基底,记
 。
。
下面定义K的“扩充”锥,因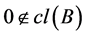 ,由凸集分离定理,存在
,由凸集分离定理,存在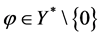 使
使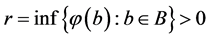 。记
。记
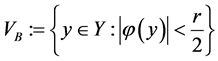 ,
,
则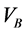 为Y中零元的开凸均衡邻域。对每一个满足
为Y中零元的开凸均衡邻域。对每一个满足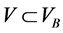 的零元的凸邻域V,记
的零元的凸邻域V,记
 ,
,
 称为K的“扩充”锥。它具有以下特性。
称为K的“扩充”锥。它具有以下特性。
引理1 [9] 1) 为点凸锥;
为点凸锥;
2)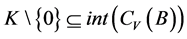 及
及 。
。
符号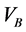 ,
, 将在整篇论文中使用。为方便起见,以下我们记
将在整篇论文中使用。为方便起见,以下我们记
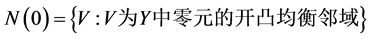 。
。
 。
。
引理2 [10] 假设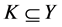 是一个含有基底B的凸锥,则
是一个含有基底B的凸锥,则
1)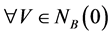 ,有
,有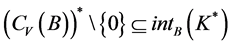 。
。
2) ,
,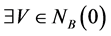 使得
使得 。
。
引理3 [11] 令M,N是Y中的两个非空凸子集,若 且
且 ,则存在
,则存在 使得
使得
 。
。
为方便讨论E-Henig真有效点与其它有效点之间的关系,以下给出了集值优化问题的几种常见的真有效点和E-真有效点的概念。
定义1 [12] 设A为Y中的一个非空子集,B为凸锥K的基底, 。如果存在
。如果存在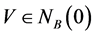 使得
使得
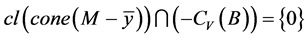 ,
,
则称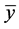 为A关于B的Henig真有效点(简称为Henig真有效点),记作
为A关于B的Henig真有效点(简称为Henig真有效点),记作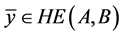 。
。
定义2 [13] 设A为Y中的一个非空子集, 是具有基底B的凸锥,
是具有基底B的凸锥,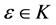 ,
, 。若存在
。若存在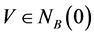 使得
使得 ,则称
,则称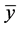 为A的ε-Henig真有效点,记作
为A的ε-Henig真有效点,记作 。
。
定义3 [14] 设E为Y中的一个非空子集,如果满足下列两个条件:
1) ;
;
2)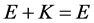 ,
,
则称E为关于K的一个改善集,将Y中改善集的全体记为 。
。
定义4 [7] 设A为Y中的一个非空子集,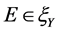 ,
,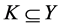 是一个闭凸锥,
是一个闭凸锥,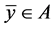 。若
。若

则称 为A的E-Benson真有效点,记作
为A的E-Benson真有效点,记作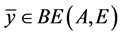 。
。
定义5 [8] 设A为Y中的一个非空子集,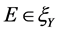 ,
, 是一个闭凸锥,
是一个闭凸锥, ,若对任意的
,若对任意的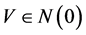 ,存在
,存在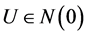 使得
使得

则称 为A的E-超有效点,记作
为A的E-超有效点,记作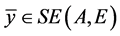 。
。
假设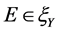 且
且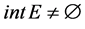 ,考虑如下集值优化问题:
,考虑如下集值优化问题:
(VP) 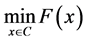
其中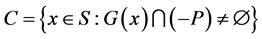 为约束集,
为约束集, ,
,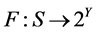 ,
,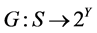 为集值映射,且
为集值映射,且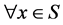 ,
,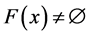 ,
,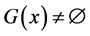 ,.若存在
,.若存在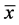 使得
使得 ,则称(VP)满足广义约束规格。
,则称(VP)满足广义约束规格。
定义6设A为Y中的非空子集, 是具有基底B的凸锥,
是具有基底B的凸锥,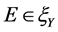 ,
,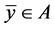 ,如果存在
,如果存在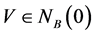 使得
使得
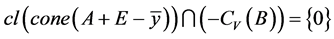 ,
,
则称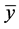 为A关于B的Henig真有效点,记作
为A关于B的Henig真有效点,记作 。
。
注1 E-Henig真有效点是一个很一般的概念,它统一了Henig真有效点及近似Henig真有效点等概念,例如:
1) 若取 ,于是
,于是 ,则E-Henig真有效点即为Henig真有效点。
,则E-Henig真有效点即为Henig真有效点。
2) 若取 ,易知
,易知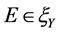 ,则E-Henig真有效点即为Henig真有效点。
,则E-Henig真有效点即为Henig真有效点。
3) 若取 ,(
,(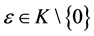 ),有
),有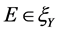 ,则E-Henig真有效点即为ε-Henig真有效点。
,则E-Henig真有效点即为ε-Henig真有效点。
4)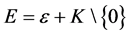 ,(
,(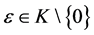 ),显然
),显然 ,则E-Henig真有效点即为ε-Henig真有效点。
,则E-Henig真有效点即为ε-Henig真有效点。
定义7 设 ,
, ,若存在
,若存在 ,使
,使 ,则称
,则称 是(VP)的E-Henig真有效解,
是(VP)的E-Henig真有效解, 为(VP)的E-Henig真有效元。
为(VP)的E-Henig真有效元。
引理4给出集值优化问题的E-Henig真有效点的几种等价刻画。
引理4设A为Y中的非空子集,B为凸锥K的基底,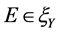 下列条件等价:
下列条件等价:
1)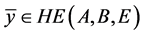 ;
;
2) 存在 使得
使得 ;
;
3) 存在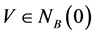 使得
使得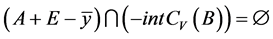 ;
;
4) 存在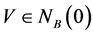 使得
使得 。
。
证明 类似于文献 [12] 中定理3.1的证明。
定理1 (存在性定理)设Y是自反的Banach空间,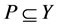 是一个锥,E为Y中的改善集,
是一个锥,E为Y中的改善集,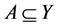 是一个无界非空的弱闭集,假设存在
是一个无界非空的弱闭集,假设存在 满足如下两个条件:
满足如下两个条件:
1)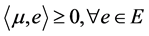 ;
;
2)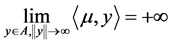 。
。
则 。
。
证明从条件2)可知,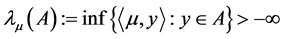 。根据下确界定义,对任意的
。根据下确界定义,对任意的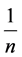 ,都存在
,都存在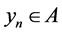 ,使得
,使得
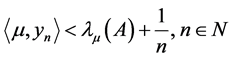 。
。
由假设2)可得,对任意的 ,
,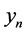 为有界的。因为A是一个弱闭集,所以不防设
为有界的。因为A是一个弱闭集,所以不防设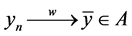 。由上式可知
。由上式可知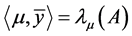 。由条件
。由条件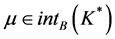 及由引理2可知,存在
及由引理2可知,存在 使得
使得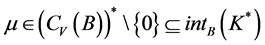 。所以对任意
。所以对任意 ,
,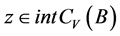 有
有
 。
。
因此 ,即
,即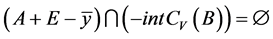 。根据引理4(3),有
。根据引理4(3),有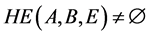 。
。
下面讨论E-Henig真有效点与E-Benson真有效点以及E-超有效点之间的关系。
命题1设 为非空子集,B为凸锥K的基底,则有
为非空子集,B为凸锥K的基底,则有 。
。
证明对任意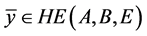 ,存在
,存在 使得
使得
 ,
,
因为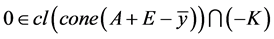 ,
,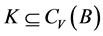 ,所以
,所以
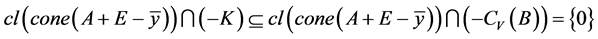 。
。
即 ,所以
,所以 。
。
命题2 设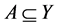 为非空子集,B为凸锥K的基底,则有
为非空子集,B为凸锥K的基底,则有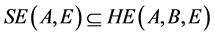 。反之不一定成立。
。反之不一定成立。
证明 因为B为凸锥K的基底,所以存在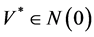 使得
使得
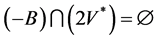 , (1)
, (1)
由于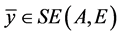 ,则上述
,则上述 ,存在
,存在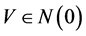 使得
使得
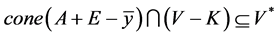
已知Y是局部凸Hausdoff空间,不失一般性,假设V是一个开凸零邻域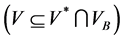 ,由(1)可知
,由(1)可知
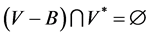 。又因为
。又因为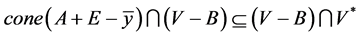 ,所以
,所以
 。
。
由于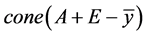 是锥,且
是锥,且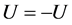 ,则
,则
 ,
,
所以 ,即
,即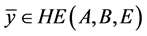 。
。
如下的例子说明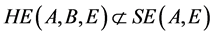 。
。
例1 令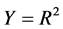 ,
, ,
, ,
,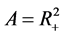 ,
, ,
, ,则
,则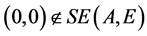 ,但
,但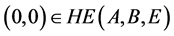 。
。
3. 标量化
下面讨论集值优化问题E-Henig真有效解的标量化问题。记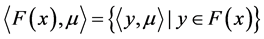 。
。
 ,其中
,其中 。
。
考虑如下标量化问题:
(VP)m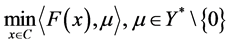 。
。
定义8 [6] 设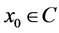 ,若存在
,若存在 使得
使得
 。 (2)
。 (2)
其中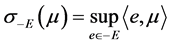 ,则称
,则称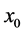 为(VP)m关于E的一个最优解,
为(VP)m关于E的一个最优解, 为(VP)m关于E的最优元。
为(VP)m关于E的最优元。
注2 若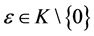 ,
, ,
,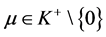 ,则
,则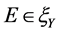 ,(2)式可退化为
,(2)式可退化为
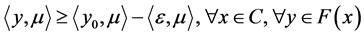 。
。
定义9 [15] 设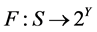 ,
,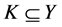 ,若
,若 是凸集,则称F是S上近似K-次类凸。
是凸集,则称F是S上近似K-次类凸。
定义10 [6] 设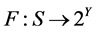 ,
,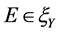 ,若
,若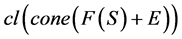 是凸集,则称F是S上近似E-次类凸。
是凸集,则称F是S上近似E-次类凸。
注3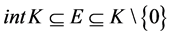 ,由文献 [15] 中的引理2.2和命题3.3可知
,由文献 [15] 中的引理2.2和命题3.3可知
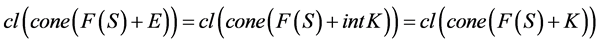 ,
,
近似E-次类凸集值映射和近似K-次类凸集值映射一致。反之,若F是近似K-次类凸的,但它不一定是近似E-次类凸的。
例2 [6] 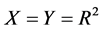 ,
,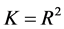 ,
,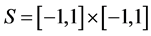 ,
,
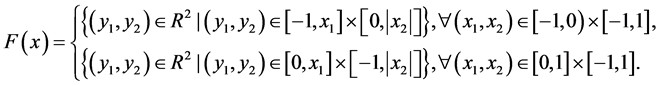
显然,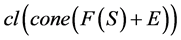 是凸集,但
是凸集,但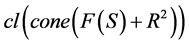 不是一个凸集。
不是一个凸集。
定理2 设B是闭凸锥K的基底, ,
, ,
,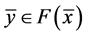 ,
,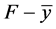 在C上近似E-次类凸。若
在C上近似E-次类凸。若 是(VP)的一个E-Henig真有效元,则存在
是(VP)的一个E-Henig真有效元,则存在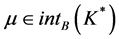 使得
使得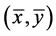 是(VP)m的E-最优元。
是(VP)m的E-最优元。
证明 由于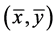 是(VP)的一个E-Henig真有效元,则存在
是(VP)的一个E-Henig真有效元,则存在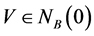 使得
使得
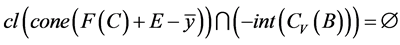 。
。
因为 在C上近似E-次类凸,所以
在C上近似E-次类凸,所以 是Y上的凸集。
是Y上的凸集。
而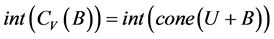 是Y上的非空凸集,由引理3知,存在
是Y上的非空凸集,由引理3知,存在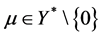 使
使
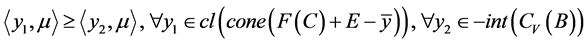 。 (3)
。 (3)
又因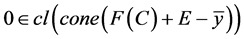 ,由(3)知
,由(3)知
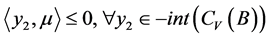 , (4)
, (4)
即 。
。
现证: 。
。
由于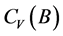 是凸锥,且
是凸锥,且 非空,则
非空,则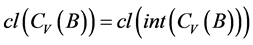 。对任意的
。对任意的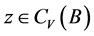 ,存在
,存在 ,有
,有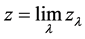 。因为
。因为 ,所以
,所以 ,即
,即 。而
。而 ,由引理2知
,由引理2知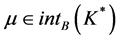 。又因为
。又因为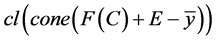 为Y中的一个锥,且
为Y中的一个锥,且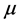 在
在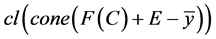 上有上下界,于是由(3)式有
上有上下界,于是由(3)式有
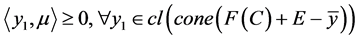 ,
,
从而
 ,
,
即
 ,
,
于是有
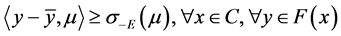 ,
,
这表明 是(VP)m的E-最优元。
是(VP)m的E-最优元。
定理3 设K是含有基底B的凸锥,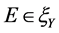 ,若存在
,若存在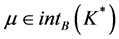 使得
使得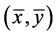 是(VP)m的E-最优元,则
是(VP)m的E-最优元,则 也是(VP)的一个E-Henig真有效元。
也是(VP)的一个E-Henig真有效元。
证明 (反证法)假设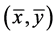 不是(VP)的E-Henig真有效元,则由引理4知,
不是(VP)的E-Henig真有效元,则由引理4知, 有
有
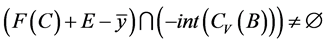 ,
,
即存在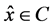 ,
,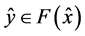 ,
,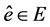 使得
使得
 。 (5)
。 (5)
因为 ,由引理2知,存在
,由引理2知,存在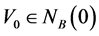 使得
使得 。由(5)得
。由(5)得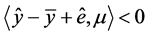 。
。
于是
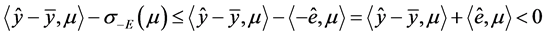 ,
,
与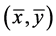 是(VP)m的E-最优元矛盾,所以
是(VP)m的E-最优元矛盾,所以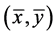 是(VP)的E-Henig真有效元。
是(VP)的E-Henig真有效元。
4. E-Henig真鞍点
本部分给出了Lagrange集值映射的E-Henig真鞍点的定义,并建立E-Henig真鞍点定理。
设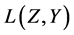 为Z到Y的连续行算子的全体,记
为Z到Y的连续行算子的全体,记
 。
。
设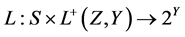 ,其中
,其中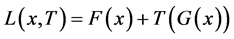 ,
,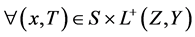 。
。
记 。
。
定义11 设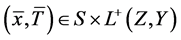 ,若
,若 ,则称
,则称 是Lagrange映射
是Lagrange映射 的一个E-Henig真鞍点。
的一个E-Henig真鞍点。
定理4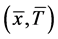 是
是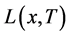 的一个E-Henig真鞍点Û存在
的一个E-Henig真鞍点Û存在 ,
,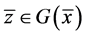 ,及
,及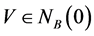 满足如下条件:
满足如下条件:
1) ;
;
2)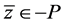 ;
;
3) ;
;
4)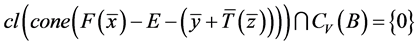 。
。
证明 “Þ”:因为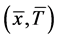 是
是 的一个E-Henig真鞍点,所以存在
的一个E-Henig真鞍点,所以存在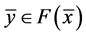 ,
, 使得
使得
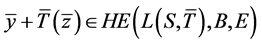 , (6)
, (6)
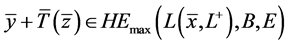 。 (7)
。 (7)
由(6)知,条件1)成立。由(7)知,存在 使
使
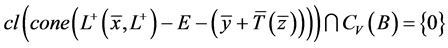 。 (8)
。 (8)
因 ,
,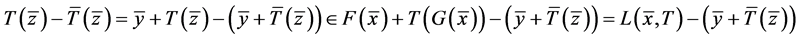 。
。
所以 。从而
。从而
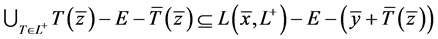 。
。
因为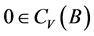 及
及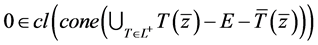 ,所以
,所以
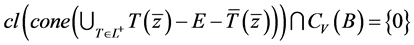 。 (9)
。 (9)
令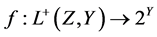 其中
其中 ,
,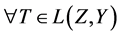 ,则(9)式可写为
,则(9)式可写为
 。
。
即 是(P)
是(P) 的一个E-Henig真有效点。因为f是线性的,所以
的一个E-Henig真有效点。因为f是线性的,所以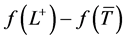 是上近似E-次类凸的。有定理2可知,存在
是上近似E-次类凸的。有定理2可知,存在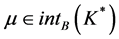 使得
使得
 。
。
所以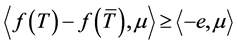 ,
, ,
, 。于是
。于是
 (10)
(10)
现证: 。
。
反证:假设 。因为P是闭凸锥,所以由强凸集分离定理知,存在
。因为P是闭凸锥,所以由强凸集分离定理知,存在 使得
使得
 。 (11)
。 (11)
在(11)中取 ,则有
,则有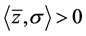 。再由(11)知
。再由(11)知
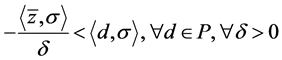 。
。
当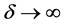 时,有
时,有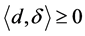 ,所以有
,所以有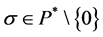 。取
。取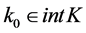 ,
, ,令
,令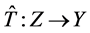
 。
。
所以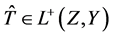 。
。
因为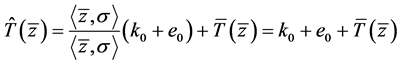 ,所以
,所以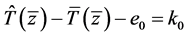 。由引理1可知,
。由引理1可知,
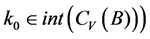 ,则有
,则有
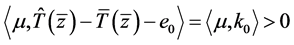 ,
,
即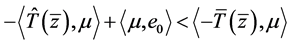 ,与(10)式矛盾,所以条件2)成立。
,与(10)式矛盾,所以条件2)成立。
由于 ,
, ,则有
,则有 。
。
现证: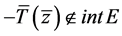 。
。
假设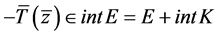 ,则存在
,则存在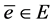 ,
,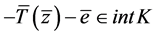 ,于是
,于是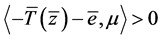 ,即
,即
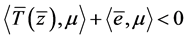 。
。
在(10)中令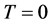 ,有
,有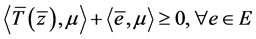 ,与上式矛盾,条件3)成立。
,与上式矛盾,条件3)成立。
在(8)中令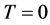 ,则条件4)成立。
,则条件4)成立。
“Ü”:由条件1)~4),只需证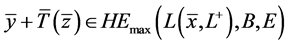 。
。
假设 ,则任意
,则任意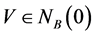 有
有
 。
。
令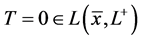 ,有
,有
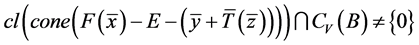 ,
,
与条件4)矛盾。所以
 。
。
定理5 若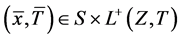 是
是 的一个E-Henig真鞍点,
的一个E-Henig真鞍点,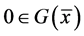 ,
, ,
, ,
,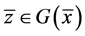 ,则
,则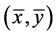 是(VP)的一个E'-Henig真有效元。
是(VP)的一个E'-Henig真有效元。
证明 因为 是
是 的一个E-Henig真鞍点,所以存在
的一个E-Henig真鞍点,所以存在 ,
, 以及
以及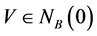 使得
使得
 。
。
因为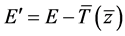 ,所以
,所以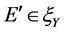 。又因为
。又因为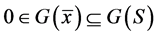 ,所以
,所以
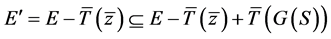 。
。
所以
 。
。
即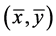 是(VP)的一个E'-Henig真有效元。
是(VP)的一个E'-Henig真有效元。
5. E-Henig对偶
称集值映射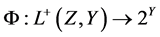 ,其中
,其中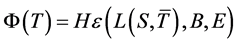 ,
, 为(VP)的E-Henig对偶映射。
为(VP)的E-Henig对偶映射。
称(VD)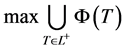 为(VP)的对偶问题。
为(VP)的对偶问题。
定义12 1)若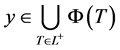 ,则称y为(VD)的一个可行点;
,则称y为(VD)的一个可行点;
2) 若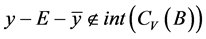 ,
,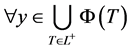 ,则称
,则称 为(VD)的E-Henig真有效点。
为(VD)的E-Henig真有效点。
定理6 设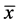 为(VP)的任意可行解,
为(VP)的任意可行解, 为(VD)的任意可行点,则存在
为(VD)的任意可行点,则存在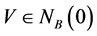 使
使
 。
。
证明 因为 为(VD)的任意可行点,则存在
为(VD)的任意可行点,则存在 使得
使得
 ,
,
由定理1存在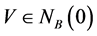 使得
使得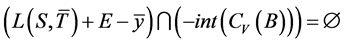 ,即
,即
 。
。
因为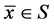 ,所以有
,所以有
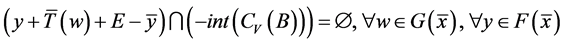 。 (12)
。 (12)
因为 为(VP)的可行解,所以
为(VP)的可行解,所以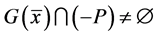 ,即存在
,即存在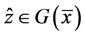 使
使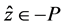 ,所以
,所以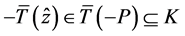 ,令(12)中
,令(12)中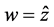 ,所以
,所以
 。
。
因为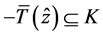 ,所以
,所以
 ,
,
即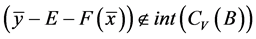 。
。
定理7 设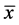 为(VP)的任意可行解,
为(VP)的任意可行解,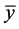 为(VD)的任意可行解,其中
为(VD)的任意可行解,其中 ,
, 为(VP)的E-Henig真有效解,
为(VP)的E-Henig真有效解, 为(VD)的E-Henig真有效点.
为(VD)的E-Henig真有效点.
证明 因为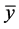 为(VD)的任意可行解,所以
为(VD)的任意可行解,所以 ,即存在
,即存在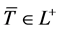 使得
使得
 。由定理1可知,存在
。由定理1可知,存在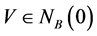 使得
使得
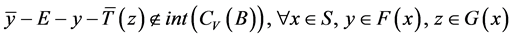 。 (13)
。 (13)
有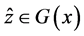 且
且 所以
所以 。令(13)中
。令(13)中 ,则有
,则有
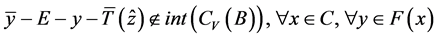 。
。
即
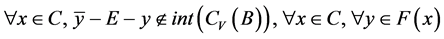 。
。
因为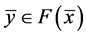 ,所以
,所以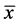 为(VP)的E-Henig真有效解。又因为
为(VP)的E-Henig真有效解。又因为 为(VP)的任意可行解,
为(VP)的任意可行解,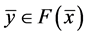 ,由定理6知,
,由定理6知,
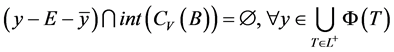 ,
,
所以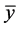 为(VD)的E-Henig真有效点。
为(VD)的E-Henig真有效点。
基金项目
国家自然科学基金资助项目(11471291)。
文章引用
林佩静,李茂旺,仇秋生. 集值优化问题的E-Henig真有效解
E-Henig Proper Efficient Solution for Set-Valued Optimization Problems[J]. 应用数学进展, 2016, 05(03): 494-504. http://dx.doi.org/10.12677/AAM.2016.53060
参考文献 (References)
- 1. Gutierrez, C., Jimenez, B. and Novo, V. (2006) A Unified Approach and Optimality Conditions for Approximate Solutions of Vector Optimization Problems. SIAM Journal on Optimization, 17, 688-710. http://dx.doi.org/10.1137/05062648X
- 2. White, D.J. (1986) Epsilon Efficiency. Journal of Optimization Theory and Applica-tions, 49, 319-337. http://dx.doi.org/10.1007/BF00940762
- 3. Loridan, P. (1984) ε-Solutions in Vector Minimization Problems. Journal of Opti-mization Theory and Applications, 43, 265-276. http://dx.doi.org/10.1007/BF00936165
- 4. Chicco, M., Mignanego, F., Pusillo, L. and Tijs, S. (2011) Vector Optimization Problems via Improvement Sets. Journal of Optimization Theory and Applications, 150, 516-529. http://dx.doi.org/10.1007/s10957-011-9851-1
- 5. Gutierrez, C., Jimenez, B. and Novo, V. (2012) Improvement Sets and Vector Optimization. European Journal of Operational Research, 223, 304-311. http://dx.doi.org/10.1016/j.ejor.2012.05.050
- 6. Zhao, K.Q., Yang, X.M. and Peng, J.W. (2013) Weak E-Optimal Solution in Vector Optimization. Taiwanese Journal of Mathematics, 17, 1287-1302.
- 7. Zhao, K.Q. and Yang, X.M. (2015) E-Benson Proper Efficiency in Vector Optimization. Optimization, 64, 739-752. http://dx.doi.org/10.1080/02331934.2013.798321
- 8. Zhou, Z.A., Yang, X.M. and Zhao, K.Q. (2016) E-Super Efficiency of Set-Valued Optimization Problems Involving Improvement Sets. Journal of Industrial and Management Optimization, 12, 1031-1039. http://dx.doi.org/10.3934/jimo.2016.12.1031
- 9. Qiu, Q.-S. (2007) Henig Efficiency in Vector Optimization with Nearly Cone-Subconvexlike Set-Valued Functions. Acta Mathematicae Applicatae Sinica, English Series, 23, 319-328. http://dx.doi.org/10.1007/s10255-007-0374-3
- 10. Gong, X.H. (2005) Optimality Conditions for Henig and Globally Proper Efficient Solutions with Ordering Cone Has Empty Interior. Journal of Mathematical Analysis and Applications, 307, 12-31. http://dx.doi.org/10.1016/j.jmaa.2004.10.001
- 11. Zalinescu, C. (2002) Convex Analysis in General Vector Spaces. World Scientific, Singapore. http://dx.doi.org/10.1142/5021
- 12. 仇秋生. 关于Henig真有效性[J]. 系统科学与数学, 2011, 31(4): 482-488.
- 13. Zhou, Z.A., Yang, X.M. and Peng, J.W. (2014) ε-Henig Proper Efficiency of Set-Valued Optimization Problems in Real Ordered Linear Spaces. Optimization Letters, 8, 1813-1827. http://dx.doi.org/10.1007/s11590-013-0667-9
- 14. Gutiérrez, C., Jiménez, B. and Novo, V. (2012) Improvement Sets and Vector Optimization. European Journal of Operational Research, 223, 304-311. http://dx.doi.org/10.1016/j.ejor.2012.05.050
- 15. Yang, X.M., Li, D. and Wang, S.Y. (2001) Near-Subconvexlikeness in Vector Optimization with Set-Valued Functions. Journal of Optimization Theory and Applications, 110, 413-427. http://dx.doi.org/10.1023/A:1017535631418