Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20796,10
pages
10.12677/AAM.2017.63046
A Research on Subway Effect in Qingdao Based on Mathematical Modeling
Chan Li, Xiang Gao*
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
*通讯作者。

Received: May 7th, 2017; accepted: May 24th, 2017; published: May 27th, 2017

ABSTRACT
This paper builds the comprehensive evaluation model through combining analytic hierarchy process with fuzzy comprehensive evaluation method to evaluate subway effect in Qingdao. Seven evaluation indexes are chosen and the evaluation results are divided into five parts. And in this model, the subway effects of Licang District, Shibei District and Shinan District in 2016 were evaluated. By using this model, we have the conclusion that the subway has a small effect on Licang District and a general effect on Shibei District. However, it has a great effect on Shinan District. Grey prediction and the least square fit method are applied to predict the value of the seven indexes in 2017. And the evaluation results of subway effect in 2017 are given based on this prediction method.
Keywords:Analytic Hierarchy Process (AHP), Fuzzy Comprehensive Evaluation, Grey Prediction, Subway Effect
青岛市地铁效应的数学建模研究
李婵,高翔*
中国海洋大学数学科学学院,山东 青岛

收稿日期:2017年5月7日;录用日期:2017年5月24日;发布日期:2017年5月27日

摘 要
本文将层次分析法与模糊综合评价方法相结合,选取了七个评价指标,将评价结果划分为“大、较大、一般、较小、小”五个等级,建立了青岛市“地铁效应”的综合评价模型。利用该模型分别对李沧区、市北区、市南区2016年的“地铁效应”做出了评价,得出李沧区“地铁效应较小”,市北区“地铁效应一般”,市南区“地铁效应大”的结论。将灰色预测模型和最小二乘拟合相结合,对各指标在2017年的取值进行预测,进而对三个区市2017年“地铁效应”进行预测,得出三个区市2017年“地铁效应大”的预测结果。
关键词 :层次分析法,模糊综合评价,灰色预测,“地铁效应”

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
地铁在城市发展中体现出巨大的“地铁效应”。一方面,地铁能够推进城市经济的发展,带动沿线商圈联动发展,增加政府的财政收入;另一方面,地铁为民众出行提供了便利,改善民众的生活环境,提高民众的生活质量。青岛地铁3号线自2015年12月16日起开始通车运营,成为青岛市首条通车运营的地铁线路,连通了青岛站与青岛北站两大交通枢纽,促进了沿线几大商圈的融合与发展,在改善民生的同时也为沿线区域带来了巨大的政治效益和经济效益。由于目前青岛市只开通了地铁3号线,其对沿线三个区市(李沧区、市北区、市南区)的“地铁效应”较整个青岛市来说更为明显。为了研究地铁3号线的开通给沿线三个区市(李沧区、市北区、市南区)带来的影响,本文建立了青岛市“地铁效应”综合评价模型,综合分析了2016年的“地铁效应”,并对2017年“地铁效应”的评价结果做出了预测。
2. 模型准备
2.1. 青岛市“地铁效应”的具体体现
本文将青岛市“地铁效应”总结为以下三个方面:
1) 政治效应
地铁作为城市重大基础设施之一,其修建过程离不开政府的大力支持,地铁建设在一定程度上影响了政府发布的政策、规定的数量。
2) 经济效应
“美国经济学家研究表明,公共产品投资中每投资1美元,国民生产总值就会增加4美元。轨道交通建设投资对国民生产总值的直接贡献率为2.63倍,即每投资1亿元,可新增2.63亿元GDP,并提供8466个就业岗位” [1] 。与此同时,经济的发展带动沿线房价的上涨,推动商圈的联动发展。
3) 民生效应
地铁的开通在为沿线带来巨大经济效益的同时,也为政府增加了税收等财政收入。与此同时,地铁的开通使得城市基础实施更加完善、经济发展更加迅速,在一定程度上促进了沿线区域常住人口的增长。
2.2. 青岛市“地铁效应”评价体系的建立
要建立青岛市“地铁效应”评价体系,首先要从众多复杂因素中筛选出关键性的评价指标,并根据评价指标之间的制约关系为指标划分层次。通过分析,本文选取了政治效应、经济效应、环境效应三个一级评价指标。为了最大程度对各指标进行定量分析,选取了政府发布政策总数、GDP增速、沿线二手房平均价格增长率、社会消费品零售总额增长率等七个可定量的二级评价指标。具体的层次结构如下图1所示。
2.3. 模型假设
1) 本文搜集的所有数据均真实可靠;
2) 假设所有数据的变化均由地铁效应引起;
3) 不考虑其他重大突发事件对“地铁效应”影响力的干扰。
3. 层次分析法确定指标权重
3.1. 层次分析法的基本原理
层次分析法是一种简单、灵活的多准则决策方法,在解决一些难以完全定量的问题上占据优势。在利用层次分析法解决问题时,首先要将问题条理化、层次化,一般将问题划分为目标层、准则层、方案层,其中准则层可包含若干子准则。在确定不同评价因素的权重时,通常采用两两比较的方法确定判断矩阵。若判断矩阵能够通过一致性检验,即一致性比例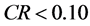 ;若判断矩阵未能通过一致性检验,则需对判断矩阵进行调整。对于符合条件的判断矩阵,求其最大特征值对应的特征向量,并进行归一化处理,即得评价因素的权重。
;若判断矩阵未能通过一致性检验,则需对判断矩阵进行调整。对于符合条件的判断矩阵,求其最大特征值对应的特征向量,并进行归一化处理,即得评价因素的权重。
3.2. 评价指标权重的确定
从“地铁效应”综合评价体系的层次结构出发,利用专家打分法,得到判断矩阵如下:
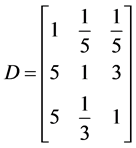 ,
,  ,
, 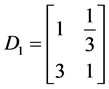 ,
,  ,
, 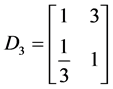
对判断矩阵进行一致性检验,结果如表1示:
对判断矩阵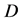 和
和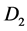 进行修正,得到新的判断矩阵
进行修正,得到新的判断矩阵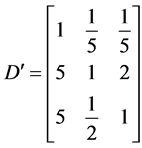 ,
, 。由此得到各层级评判指标的权向量
。由此得到各层级评判指标的权向量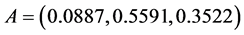 ,
,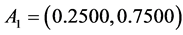 ,
,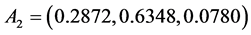 ,
,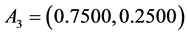 。
。
4. 青岛市“地铁效应”模糊综合评价模型
4.1. 多层次模糊综合评价法的基本步骤
多层次模糊综合评价法主要有以下七个步骤:
1) 确定被评价对象集合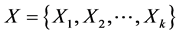 ;
;
2) 确定被评价对象的因素论域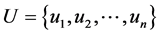 ,可以根据
,可以根据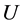 中元素的特点将其划分为
中元素的特点将其划分为 个子集
个子集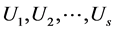 ;
;
3) 确定评语等级论域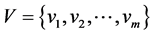 ;
;
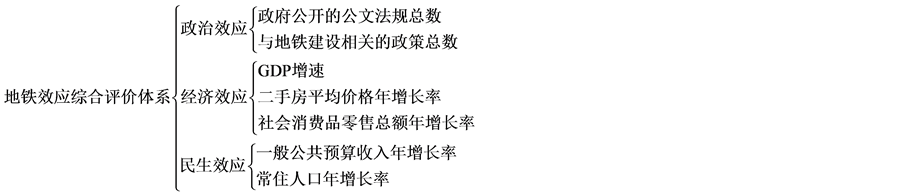
Figure 1. Comprehensive evaluation system of subway effect
图1. “地铁效应”综合评价体系
Table 1. Results of consistency check
表1. 一致性检验结果
4) 对每个因素集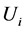 ,确定模糊评价矩阵
,确定模糊评价矩阵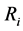 ;
;
5) 确定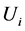 中各因素的权重,给出权向量
中各因素的权重,给出权向量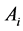 ,得到一级评价矩阵
,得到一级评价矩阵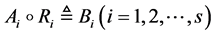 ;
;
6) 将每个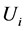 视为一个因素,则
视为一个因素,则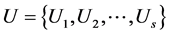 为单因素集,确定其模糊评价矩阵并记为
为单因素集,确定其模糊评价矩阵并记为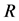 ,则有
,则有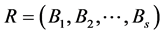 ,根据各因素的重要程度为其分配权重,记权向量为
,根据各因素的重要程度为其分配权重,记权向量为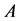 ;
;
7) 得到二级模糊综合评价矩阵 ,根据最大隶属度原则确定评价对象的评语等级。
,根据最大隶属度原则确定评价对象的评语等级。
4.2. 青岛市“地铁效应”综合评价模型的建立 [2]
4.2.1. 因素集和评语集的确定
根据上文给出的青岛市“地铁效应”综合评价体系,得到如下图所示的二级模糊综合评价模型,
由图2可知,因素论域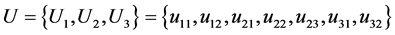 ,其中
,其中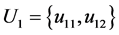 ,
,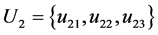 ,
,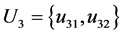 。本文将对“地铁效应”评价划分为“小”、“较小”、“一般”、“较大”、“大”五个等级,故有评语等级论域
。本文将对“地铁效应”评价划分为“小”、“较小”、“一般”、“较大”、“大”五个等级,故有评语等级论域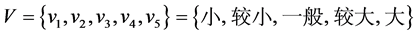 。为了研究青岛市“地铁效应”对沿线不同区域的影响,取评价对象集合
。为了研究青岛市“地铁效应”对沿线不同区域的影响,取评价对象集合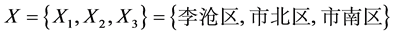 。
。
4.2.2. 各评价指标隶属度的确定
本文采用构造隶属函数的方法确定隶属度,为方便起见,隶属函数均为梯形型 [3] 。设某一评价指标的取值为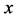 ,五个临界点从小到大分别为
,五个临界点从小到大分别为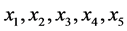 ,隶属函数为
,隶属函数为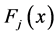 ,则有
,则有
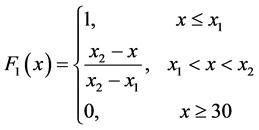
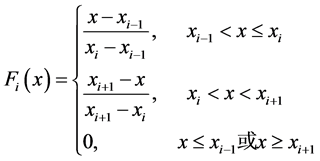 ,
, 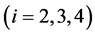
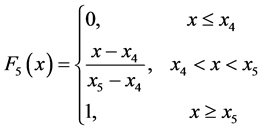 首先对各个评价指标的取值进行分段,给出不同取值对应的“地铁效应”评价等价,具体分段方法见下表2。通过查询青岛统计信息网和青岛市统计年鉴,得到三个区市(李沧区、市北区、市南区)各评价指标在2016年的取值如下表3。
首先对各个评价指标的取值进行分段,给出不同取值对应的“地铁效应”评价等价,具体分段方法见下表2。通过查询青岛统计信息网和青岛市统计年鉴,得到三个区市(李沧区、市北区、市南区)各评价指标在2016年的取值如下表3。
Figure 2. Fuzzy comprehensive evaluation model
图2. 模糊综合评价模型
Table 2. Subsection value of evaluation indexes
表2. 各评价指标取值分段
Table 3. Value of evaluation indexes in 2016
表3. 2016年各评价指标取值
当评判对象为 时,模糊矩阵为
时,模糊矩阵为

当评判对象为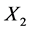 时,模糊矩阵为
时,模糊矩阵为
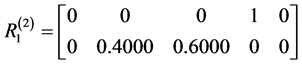
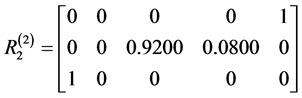
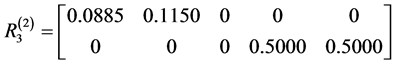
当评判对象为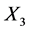 时,模糊矩阵为
时,模糊矩阵为


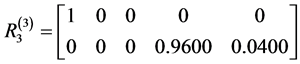
4.2.3. 青岛市“地铁效应”综合评价结果
评判对象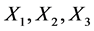 的二级模糊综合评价矩阵分别为
的二级模糊综合评价矩阵分别为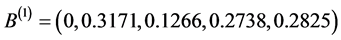 ,
,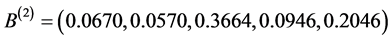 ,
,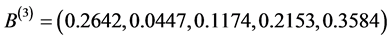 ,根据最大隶属度原则,得到李沧区、市北区、市南区的2016年“地铁效应”综合评价结果如下表4。
,根据最大隶属度原则,得到李沧区、市北区、市南区的2016年“地铁效应”综合评价结果如下表4。
即李沧区“地铁效应”一般,市北区“地铁效应”一般,市北区“地铁效应”较大。
5. 青岛市“地铁效应”预测模型
5.1. 灰色预测模型的基本原理
灰色预测模型以GM(1,1)模型为基础,将随机过程当做灰色过程,随机变量当做灰色变量,适用于解决历史数据较少的时间序列预测问题。灰色预测的具体步骤如下:
1) 对原始数据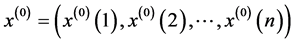 进行累加运算,得到累加数列
进行累加运算,得到累加数列 ;
;
Table 4. Results of comprehensive evaluation on subway effect
表4. “地铁效应”综合评价结果
2) 计算级比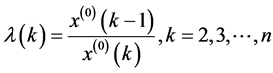 ,检验其是否落在可容覆盖区间内;
,检验其是否落在可容覆盖区间内;
3) 建立白化微分方程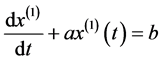 并求解,得到预测值;
并求解,得到预测值;
4) 残差检验,设残差为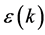 ,如果
,如果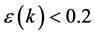 ,可认为达到一般要求,如果
,可认为达到一般要求,如果 ,可认为达到较高要求;
,可认为达到较高要求;
5) 级比偏差检验,定义级比偏差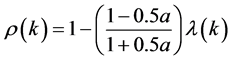 ,如果
,如果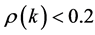 ,可认为达到一般要求,如果
,可认为达到一般要求,如果 ,可认为达到较高要求。
,可认为达到较高要求。
5.2. 最小二乘拟合的基本原理
最小二乘拟合法是最常用的曲线拟合法。设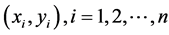 为平面上的
为平面上的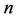 个点,
个点,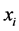 互不相同,
互不相同,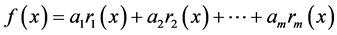 ,其中
,其中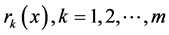 是一组线性无关的函数,
是一组线性无关的函数,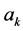 是待定系数,采用最小二乘准则进行拟合,即使
是待定系数,采用最小二乘准则进行拟合,即使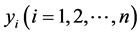 与
与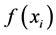 距离的平方和最小。
距离的平方和最小。
记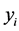 与
与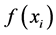 距离的平方和为
距离的平方和为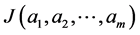 ,利用极值的必要条件便可求得使
,利用极值的必要条件便可求得使 达到最小值的
达到最小值的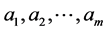 。
。
5.3. 评价指标的预测结果
由于文中指标的历史数据较少,导致样本容量较小,不满足常用的预测方法(如时间序列法、神经网络预测法等)大容量样本的要求。因此,本文将采用灰色预测方法对上述七个评价因素2017年的取值进行预测,要求预测相对误差小于0.2。当灰色预测的相对误差不能满足要求时,则采用最小二乘拟合的方法进行预测,同样要求预测的相对误差小于0.2。最后根据各指标的预测值预测李沧区、市北区、市南区在2017年的“地铁效应”。(各评价指标的历史数据见附录)
各评价指标的预测结果(精确到小数点后四位)如下表5所示。
5.4. 青岛市2017年“地铁效应”预测结果
预测时,保持各评价指标的权重分配不变,将各评价指标的预测值代入对应的隶属函数,得到新的模糊矩阵。将权向量与新的模糊矩阵合成,根据最大隶属度原则,即可得到三个区市2017年“地铁效应”的综合评价结果,如表6所示。
6. 模型总结
由青岛市“地铁效应”综合评价模型可知,李沧区、市北区、市南区2016年“地铁效应”综合评价等级分别为“小”、“一般”、“大”,即“地铁效应”对市南区的影响最大,这与市南区作为青岛市的政治、经济、金融中心,经济发达、城市基础设施完善、民生保障措施全面有着密切的关系。
由预测模型可知,李沧区、市北区、市南区2017年“地铁效应”评价等级的预测结果分别为“大”、“大”、“大”,这说明地铁对区域发展的影响力与时间成正相关关系,时间越长,“地铁效应”越明
Table 5. Prediction value of evaluation indexes
表5. 各评级指标预测值
Table 6. Prediction results of comprehensive evaluation on subway effect in 2017
表6. 2017年“地铁效应”综合评价预测结果
显。李沧区虽然在三个区市中政治、经济基础相对薄弱,但其政治、经济发展的上升空间也相对较大,地铁开通给其区域发展带来的长期效应更明显。市南区自身基础较好,在各方面都处于领先地位,导致“地铁效应”对其发展的促进作用长期停留在某一水平,上升空间较小。
总之,地铁的开通对沿线区域的政治、经济、民生产生巨大的积极影响。政府应该加大对地铁项目建设的支持力度,积极推进城市基础设施建设,继续改善和保障民生。
文章引用
李婵,高翔. 青岛市地铁效应的数学建模研究
A Research on Subway Effect in Qingdao Based on Mathematical Modeling[J]. 应用数学进展, 2017, 06(03): 398-407. http://dx.doi.org/10.12677/AAM.2017.63046
参考文献 (References)
- 1. 李婧. 城市轨道交通社会效益的模糊综合评价[J]. 科技与经济, 2007, 9(3): 89-91.
- 2. 佟玲, 张洪强, 刘淑娟, 金晓燕. 轨道交通对城市影响的模糊综合评价[J]. 交通科技与经济, 2011, 13(4): 79-82.
- 3. 肖和华, 李谆. 城市轨道交通综合评价研究——基于改进AHP的多级模糊综合评价方法[J]. 交通标准化, 2009(23): 28-31.
附录
各评价指标的历史数据如下表所示,指标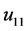 和指标
和指标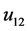 的历史数据来源于青岛政务网 (http://www.qingdao.gov.cn/n172/),余下指标的历史数据来源于青岛统计信息网 (http://www.stats-qd.gov.cn/statsqd/index/index.shtml)。
的历史数据来源于青岛政务网 (http://www.qingdao.gov.cn/n172/),余下指标的历史数据来源于青岛统计信息网 (http://www.stats-qd.gov.cn/statsqd/index/index.shtml)。
Table 7. Historical data of evaluation indexes
表7. 各评级指标历史数据
期刊投稿者将享受如下服务:
1.投稿前咨询服务 (QQ、微信、邮箱皆可)
2.为您匹配最合适的期刊
3.24小时以内解答您的所有疑问
4.友好的在线投稿界面
5.专业的同行评审
6.知网检索
7.全网络覆盖式推广您的研究
投稿请点击:http://www.hanspub.org/Submission.aspx
期刊邮箱:aam@hanspub.org
