Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23177,6
pages
10.12677/AAM.2017.69145
Comparison of Calculation Methods for Confined Steady Well Flow Based on Finite Difference Method
Siyu Zhang, Deliang Zhou, Jingyi Sun
School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Dec. 3rd, 2017; accepted: Dec. 20th, 2017; published: Dec. 27th, 2017

ABSTRACT
Based on finite difference method, we use early method, well level optimization method and polishing singular point method to calculate the well level in example respectively. The example is calculated and compared. The well level calculated by polishing singular point method is closest to the real well level.
Keywords:Finite Difference Method, Well Level Calculation, Comparison, Polishing Singular Point Method
基于有限差分法的承压稳定井流计算方法的 比较
张思宇,周德亮,孙婧祎
辽宁师范大学数学学院,辽宁 大连
收稿日期:2017年12月3日;录用日期:2017年12月20日;发布日期:2017年12月27日

摘 要
分别用有限差分法的早期方法、井水位优化方法和奇点磨光法计算实例中井水位。由实例计算并比较显示,奇点磨光法计算得到的井水位与井处真实水位最接近。
关键词 :有限差分法,井水位计算,比较,奇点磨光

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在水文地质实践中,很多情况下都涉及到井水位计算问题。它不仅关系到地下水资源的合理开发与利用,而且还关系到水源地建设的投资。对于井水位的计算,使用最广泛的方法为有限差分法 [1] [2] ,由地下水动力学理论和实际经验可知,井流是径向流动的,所以按有限差分法处理井流时,模拟得到的井点水位并不能代表井中的真实水位,这为动态分析地下水井水位运动的变化规律及水资源的开发与利用带来了负面影响。为解决这一问题,1967年Prickett提出了针对正方形网格井点处水位的校正公式。1978年Peacemen基于Theim公式提出了Well Index校正方法。1984年李贻祖,陈平等基于有限元的模拟,通过井周的特殊划分求导出井中水位修正公式。1990年陈崇希,唐仲华等根据不稳定流理论提出了正方形差分网格的井中水位校正公式。2003年曹洪,尹小玲等在李贻祖方法的基础上,将单元按等分圆周划分得出井中水位修正公式。本文针对有限差分法的早期方法 [3] 、井水位优化方法 [4] 和奇点磨光法 [5] 这三种井水位计算方法进行描述,并将它们在一具体实例中的计算结果与井中真实水位进行比较。
2. 井水位早期计算方法
考虑如下承压稳定井流问题
其中, , 为导水系数, 为水头函数, 、 、 是已知函数, 为第 口井的开采量, 为第 口井的半径。
对于有限差分法,先进行网格剖分,取定沿 轴, 轴的步长 和 ,做两族与坐标轴平行的直线: , ; , ,两族直线的交点 称为节点,记为 。对于区域内的节点,分别用沿 , 方向的二阶中心差商代替 和 ,即
同理,对于在二类边界 和 上的节点,也可以用二阶中心差商代替节点在其外法线方向导数,即将(2.1)~(2.4)转化为求解如下问题
联立(2.5)、(2.6)和(2.7)解出 ,即得到承压稳定井流问题的解。
井水位早期计算方法是对(2.1)~(2.4)进行离散,将原问题转化为如下问题
再用 近似井点处平均流量,即(2.8)式中右端项量,其中 是井点附近网格对偶剖分形成的面积。
3. 井水位优化方法
如图1,依据有限差分法在井点四周布置间距为 、 的矩形网格,假定抽水井所在节点 与周围节点间已经形成了拟稳定流动(即水位随时间变化,而水力坡度不随时间变化的不稳定流动)。由Theis公式的近似式可知, 点水位 和 点水位 与井中的水位 之间满足下述关系:
(3.1)
(3.2)
其中, 为抽水井的流量; 为导水系数; 为井的半径。
同理,得到节点 和 处水位 、 ,
(3.3)
(3.4)
将有限差分法模拟得到的节点 处的水位记为 ,利用差分公式计算的从四周进入 点处的流量与水井的流量是相同,所以有
(3.5)
把上述 , , , 的表达式都代入到(3.5)式,可得到如下优化公式

Figure 1. Plane difference grid near well point
图1. 井点附近平面差分网格
(3.6)
当取 时,(3.6)式可简化为
(3.7)
一般情况下, 会远大于 ,所以 ,这就是有限差分法得到的井中水位偏高的原因。
4. 奇点磨光法
奇点磨光法的基本思想是将问题(2.1)~(2.4)化成求解一个无井存在且方程右端充分光滑的问题。为此,在区域 内定义辅助函数 ,即相对于每一个井造一个定义在区域 上的辅助函数 ,为使辅助函数在抽水井处的奇性与水头函数 在抽水井处的奇性相同,函数 应满足的条件为:(1) (2); ;(3) ;(4) , , 是以井点 为心的圆周半径,要求该圆周不能越过 的边界 。
令 ,对于问题(2.1)~(2.4)就转变为求解下述问题
基于有限差分法求得 ,即得到问题(2.1)~(2.4)的解 。
设 光滑无奇性。为保证求解精度,函数 的选择除了要满足前述4个条件外,还要能使方程(4.1)的右端项 无奇性且连续。
5. 数值算例
为比较上述三种方法的求解效果,具体考虑如下混合边界井流计算问题。存在一个长为 ,宽为 的矩形区域,东西边界 和 为定水头边界,南北边界 和 为隔水边界。承压含水层的导水系数 , 为水头函数。在区域内有一抽水井以 的流量抽水,抽水井的中心坐标 ,井的半径为 ,井的边界设为 。
针对奇点磨光法,根据辅助函数 满足的条件,取 的紧支域半径为 ,利用待定系数法可得到
,
其中 。三种计算方法得到的井水位的近似解与井中真实水位的绝对误差分别如图2、图3和图4所示。
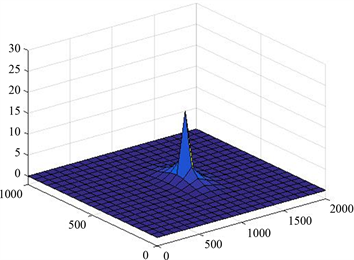
Figure 2. Early method approximate water level and true water level error
图2. 早期方法近似水位与真实水位误差
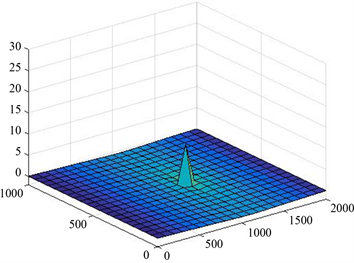
Figure 3. Water level optimization method approximate water level and true water level error
图3. 井水位优化方法近似水位与真实水位误差

Figure 4. Approximate water level by singular point smoothing method and true water level error
图4. 奇点磨光法近似水位与真实水位误差
6. 结语
由实例计算得出,早期方法在井点处的计算误差较大;井水位优化方法可以达到很好的模拟效果但只适合用于矩形网格,对实际应用具有一定的局限性;奇点磨光法的求解精度高,同时很好的处理了井点处奇异性问题,对于实际应用没有网格划分上的限制。因此,对于井水位计算奇点磨光法是一种值得推广的方法。
文章引用
张思宇,周德亮,孙婧祎. 基于有限差分法的承压稳定井流计算方法的比较
Comparison of Calculation Methods for Confined Steady Well Flow Based on Finite Difference Method[J]. 应用数学进展, 2017, 06(09): 1201-1206. http://dx.doi.org/10.12677/AAM.2017.69145
参考文献 (References)
- 1. 张宏仁. 解地下水渗流问题的有限差分方法(二) [J]. 水文地质工程地质, 1980(2): 58-61.
- 2. 陈崇希, 等. 地下水流数值模拟理论方法及模型设计[M]. 北京: 地质出版社, 2014.
- 3. 孙讷正. 地下水流的数学模型和数值方法[M]. 北京: 地质出版社, 1981: 110.
- 4. 陈崇希, 王旭升, 胡立堂. 地下水数值模拟中抽水井水位校正[J]. 水利学报, 2007, 38(4): 481-485.
- 5. 吉林大学数学系计算服务站地下水小组. 地下水非稳定流计算的有限元方法(I) [J]. 吉林大学学报, 1977(1): 15-27.